数学人教A版(2019)必修第一册3.1.1函数的概念 课件(共37张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.1.1函数的概念 课件(共37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 13:15:41 | ||
图片预览











文档简介
(共37张PPT)
1、初中学习的函数概念:
设在一个变化的过程中,有两个变量x和y,如果给定了一个x值,相应地就有唯一确定的一个y值与之对应,那么我们就称y是x的函数,其中x是自变量,y是因变量.它们描述的是两个变量之间的依赖关系.
2、初中学习过哪些函数?
复习巩固
3.1.1 函数的概念
第三章 函数的概念与性质
课前准备:①课本、练习册 ②导学案
③日清单(过关条)④红黑双色笔
3.1 函数的概念及其表示
学习目标
1.理解函数的概念,了解构成函数的三要素
2.会求一些简单函数的定义域,并会用区间表示
3.掌握同一个函数,并会判断
4.会求简单函数的函数值和值域,并会用区间表示值域(重点)
【自学指导】(5分钟)
请回答以下问题:
1.阅读课本60页的问题1和61页的问题2,并思考它们有什么异同点?
提示:它们有相同的解析式,也就是对应关系.但它们有不同的实际背景,变量的取值范围也不同.
2.请同学们继续阅读课本上的问题3和问题4,它们分别是函数吗?如果是,请指出它们与问题1和问题2中的函数的区别.
提示:是函数.由图象和表格呈现出来的变量间的对应关系比解析式更直观、形象.
问题导思
3.通过对课本中的4个问题的分析,你能说出它们有什么不同点和共同点吗?
提示:不同点:课本中的问题1,2是用解析式刻画两个变量之间的对应关系,问题3是用图象刻画两个变量之间的对应关系,问题4是用表格刻画两个变量之间的对应关系.共同点:①都包含两个非空的实数集,分别用A,B来表示;②两个实数集之间都有一种确定的对应关系;③对于数集A中的任意一个数x,按照对应关系,在数集B中都有唯一确定的数y和它对应.
函数的概念
新知形成
概念 一般地,设A,B是非空的________,如果对于集合A中的_____________,按照某种______的对应关系f,在集合B中都有__________的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数
三要素 对应关系 y=f(x),x∈A
定义域 的取值范围A
值域 与x的值相对应的___的值的集合{f(x)|x∈A}
实数集
任意一个数x
确定
唯一确定
x
y
【自学指导】(5分钟)
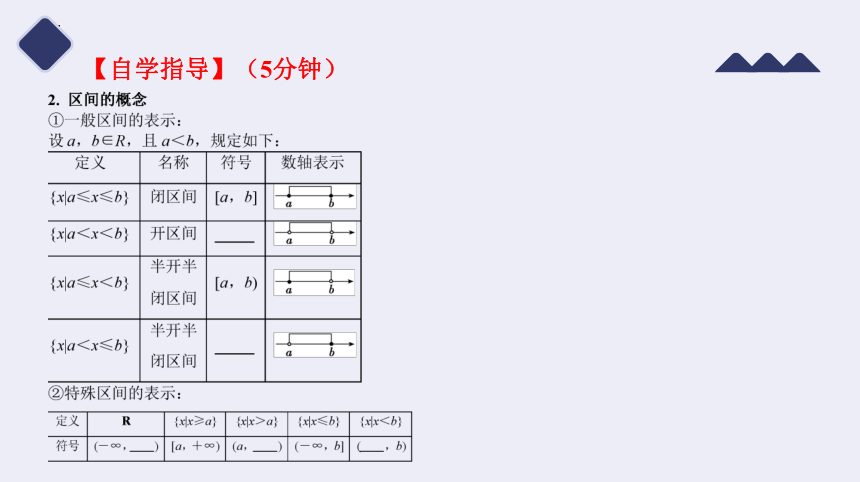
1.一般区间的表示
设a,b∈R,且a<b,规定如下:
新知形成
(a,b)
(a,b]
2.特殊区间的表示
定义 R {x|x≥a} {x|x>a} {x|x≤b} {x|x<b}
符号 (-∞,______) [a,+∞) (a,______) (-∞,b] (______,b)
+∞
+∞
-∞
【自学指导】(5分钟)
请回答以下问题:
1.构成函数的要素有哪些?
提示:定义域、对应关系和值域.
2.结合函数的定义,如何才能确定一个函数?
提示:有确定的定义域和对应关系,则此时值域唯一确定.
问题导思
新知形成
前提条件 定义域______
__________完全一致
结论 这两个函数是同一个函数
相同
对应关系
【自学检测】-----------------------(6分钟)
(多选)下列集合A到集合B的对应关系f是函数的是
A.A={-1,0,1},B={0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开方
C.A=Z,B=Q,f:A中的数取倒数
D.A=R,B={x|x≥0},f:A中的数取绝对值
√
√
按照函数定义,选项B中,集合A中的元素1对应集合B中的元素±1,不符合函数定义中一个自变量的值对应唯一的函数值的条件;选项C中,集合A中的元素0取倒数没有意义,也不符合函数定义中集合A中任意元素都对应着唯一的函数值的要求;选项A和D符合函数的定义.
1
【自学检测】-----------------------(6分钟)
2.设M={x|0≤x≤2},N={y|0≤y≤2},给出下列五个图形:
其中,能表示从集合M到集合N的函数关系的个数是
A.0 B.1
C.2 D.3
√
①中,因为在集合M中当1②中,对于集合M中的任意一个数x,在N中都有唯一的数与之对应,所以②可以表示;
③中,x=2对应元素y=3 N,所以③不能表示;
④中,当x=1时,在N中有两个元素与之对应,所以④不能表示;
⑤中,对于集合M中的任意一个数x,在N中都有唯一的数与之对应,所以⑤可以表示.故选C.
1.判断一个对应关系是否为函数的方法
方法技巧
2.根据图形判断对应关系是否为函数的方法
(1)任取一条垂直于x轴的直线l;
(2)在定义域内平行移动直线l;
(3)若直线l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.
方法技巧
3.求已知函数的定义域:
已知解析式求函数定义域的一般方法
1.如果f(x)是整式,其定义域是实数集R(通常省略不写).
2.如果f(x)是分式,其定义域是使分母不为0的实数集合.
3.如果f(x)是二次根式(偶次根式),其定义域是使根号内的式子不小于0的实数集合.
4.如果f(x)是由以上几部分式子构成的,其定义域是使各部分式子都有意义的实数集合.
5.f(x)=x0的定义域是{x|x∈R,且x≠0}.
方法技巧
把下列数集用区间表示:
(1){x|x≥-1};
{x|x≥-1}=[-1,+∞).
例1
(2){x|x<0};
{x|x<0}=(-∞,0).
(3){x|-1{x|-1(4){x|0{x|0用区间表示数集时应注意的问题
1.区间左端点值小于右端点值.
2.区间两端点之间用“,”隔开.
3.含端点值的一端用中括号,不含端点值的一端用小括号.
4.以“-∞”“+∞”为区间的一端时,这端必须用小括号.
方法技巧
(链接教材P66例3)(多选)下列各组函数是同一个函数的是
例2
√
√
判断两个函数是否为同一个函数的三个步骤
[提醒] (1)在化简解析式时,必须是等价变形;(2)与用哪个字母表示无关.
方法技巧
应用一 抽象函数的定义域
(1)函数y=f(x)的定义域是[-1,3],则f(2x+1)的定义域为________.
令-1≤2x+1≤3,解得-1≤x≤1,
所以f(2x+1)的定义域为[-1,1].
[-1,1]
(2)若函数y=f(3x+1)的定义域为[-2,4],则y=f(x)的定义域为_________.
由题意知,-2≤x≤4,所以-5≤3x+1≤13,
所以y=f(x)的定义域为[-5,13].
[-5,13]
例3
求抽象函数定义域的方法
1.已知f(x)的定义域为[a,b],求f(g(x))的定义域时,不等式a≤g(x)≤b的解集即定义域.
2.已知f(g(x))的定义域为[c,d],求f(x)的定义域时,求出g(x)在[c,d]上的范围(值域)即定义域.
方法技巧
应用二 函数的值域
求下列函数的值域:
(1)f(x)=2x+1,x∈{1,2,3,4,5};
例4
x∈{1,2,3,4,5},分别代入求值,可得函数的值域为{3,5,7,9,11}.
(2)f(x)=x2-4x+6,x∈[1,5);
(图象法)f(x)=x2-4x+6=(x-2)2+2,因为x∈[1,5),如图所示,所以函数f(x)的值域为[2,11).
求函数值域的常用方法
1.配方法:此方法是求“二次函数类”值域的基本方法,即把函数通过配方转化为能直接看出其值域的函数的方法.
2.图象法:通过画出函数的图象,由图形的直观性获得函数的值域.
3.分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域.
方法技巧
要使函数有意义,则x+2≠0,解得x≠-2,
所以函数f(x)的定义域是{x|x≠-2}.
索引
高考链接
当堂训练
(15分钟)(满分20分)
请同学们完成当堂训练的题目
1、初中学习的函数概念:
设在一个变化的过程中,有两个变量x和y,如果给定了一个x值,相应地就有唯一确定的一个y值与之对应,那么我们就称y是x的函数,其中x是自变量,y是因变量.它们描述的是两个变量之间的依赖关系.
2、初中学习过哪些函数?
复习巩固
3.1.1 函数的概念
第三章 函数的概念与性质
课前准备:①课本、练习册 ②导学案
③日清单(过关条)④红黑双色笔
3.1 函数的概念及其表示
学习目标
1.理解函数的概念,了解构成函数的三要素
2.会求一些简单函数的定义域,并会用区间表示
3.掌握同一个函数,并会判断
4.会求简单函数的函数值和值域,并会用区间表示值域(重点)
【自学指导】(5分钟)
请回答以下问题:
1.阅读课本60页的问题1和61页的问题2,并思考它们有什么异同点?
提示:它们有相同的解析式,也就是对应关系.但它们有不同的实际背景,变量的取值范围也不同.
2.请同学们继续阅读课本上的问题3和问题4,它们分别是函数吗?如果是,请指出它们与问题1和问题2中的函数的区别.
提示:是函数.由图象和表格呈现出来的变量间的对应关系比解析式更直观、形象.
问题导思
3.通过对课本中的4个问题的分析,你能说出它们有什么不同点和共同点吗?
提示:不同点:课本中的问题1,2是用解析式刻画两个变量之间的对应关系,问题3是用图象刻画两个变量之间的对应关系,问题4是用表格刻画两个变量之间的对应关系.共同点:①都包含两个非空的实数集,分别用A,B来表示;②两个实数集之间都有一种确定的对应关系;③对于数集A中的任意一个数x,按照对应关系,在数集B中都有唯一确定的数y和它对应.
函数的概念
新知形成
概念 一般地,设A,B是非空的________,如果对于集合A中的_____________,按照某种______的对应关系f,在集合B中都有__________的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数
三要素 对应关系 y=f(x),x∈A
定义域 的取值范围A
值域 与x的值相对应的___的值的集合{f(x)|x∈A}
实数集
任意一个数x
确定
唯一确定
x
y
【自学指导】(5分钟)
1.一般区间的表示
设a,b∈R,且a<b,规定如下:
新知形成
(a,b)
(a,b]
2.特殊区间的表示
定义 R {x|x≥a} {x|x>a} {x|x≤b} {x|x<b}
符号 (-∞,______) [a,+∞) (a,______) (-∞,b] (______,b)
+∞
+∞
-∞
【自学指导】(5分钟)
请回答以下问题:
1.构成函数的要素有哪些?
提示:定义域、对应关系和值域.
2.结合函数的定义,如何才能确定一个函数?
提示:有确定的定义域和对应关系,则此时值域唯一确定.
问题导思
新知形成
前提条件 定义域______
__________完全一致
结论 这两个函数是同一个函数
相同
对应关系
【自学检测】-----------------------(6分钟)
(多选)下列集合A到集合B的对应关系f是函数的是
A.A={-1,0,1},B={0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开方
C.A=Z,B=Q,f:A中的数取倒数
D.A=R,B={x|x≥0},f:A中的数取绝对值
√
√
按照函数定义,选项B中,集合A中的元素1对应集合B中的元素±1,不符合函数定义中一个自变量的值对应唯一的函数值的条件;选项C中,集合A中的元素0取倒数没有意义,也不符合函数定义中集合A中任意元素都对应着唯一的函数值的要求;选项A和D符合函数的定义.
1
【自学检测】-----------------------(6分钟)
2.设M={x|0≤x≤2},N={y|0≤y≤2},给出下列五个图形:
其中,能表示从集合M到集合N的函数关系的个数是
A.0 B.1
C.2 D.3
√
①中,因为在集合M中当1
③中,x=2对应元素y=3 N,所以③不能表示;
④中,当x=1时,在N中有两个元素与之对应,所以④不能表示;
⑤中,对于集合M中的任意一个数x,在N中都有唯一的数与之对应,所以⑤可以表示.故选C.
1.判断一个对应关系是否为函数的方法
方法技巧
2.根据图形判断对应关系是否为函数的方法
(1)任取一条垂直于x轴的直线l;
(2)在定义域内平行移动直线l;
(3)若直线l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.
方法技巧
3.求已知函数的定义域:
已知解析式求函数定义域的一般方法
1.如果f(x)是整式,其定义域是实数集R(通常省略不写).
2.如果f(x)是分式,其定义域是使分母不为0的实数集合.
3.如果f(x)是二次根式(偶次根式),其定义域是使根号内的式子不小于0的实数集合.
4.如果f(x)是由以上几部分式子构成的,其定义域是使各部分式子都有意义的实数集合.
5.f(x)=x0的定义域是{x|x∈R,且x≠0}.
方法技巧
把下列数集用区间表示:
(1){x|x≥-1};
{x|x≥-1}=[-1,+∞).
例1
(2){x|x<0};
{x|x<0}=(-∞,0).
(3){x|-1
1.区间左端点值小于右端点值.
2.区间两端点之间用“,”隔开.
3.含端点值的一端用中括号,不含端点值的一端用小括号.
4.以“-∞”“+∞”为区间的一端时,这端必须用小括号.
方法技巧
(链接教材P66例3)(多选)下列各组函数是同一个函数的是
例2
√
√
判断两个函数是否为同一个函数的三个步骤
[提醒] (1)在化简解析式时,必须是等价变形;(2)与用哪个字母表示无关.
方法技巧
应用一 抽象函数的定义域
(1)函数y=f(x)的定义域是[-1,3],则f(2x+1)的定义域为________.
令-1≤2x+1≤3,解得-1≤x≤1,
所以f(2x+1)的定义域为[-1,1].
[-1,1]
(2)若函数y=f(3x+1)的定义域为[-2,4],则y=f(x)的定义域为_________.
由题意知,-2≤x≤4,所以-5≤3x+1≤13,
所以y=f(x)的定义域为[-5,13].
[-5,13]
例3
求抽象函数定义域的方法
1.已知f(x)的定义域为[a,b],求f(g(x))的定义域时,不等式a≤g(x)≤b的解集即定义域.
2.已知f(g(x))的定义域为[c,d],求f(x)的定义域时,求出g(x)在[c,d]上的范围(值域)即定义域.
方法技巧
应用二 函数的值域
求下列函数的值域:
(1)f(x)=2x+1,x∈{1,2,3,4,5};
例4
x∈{1,2,3,4,5},分别代入求值,可得函数的值域为{3,5,7,9,11}.
(2)f(x)=x2-4x+6,x∈[1,5);
(图象法)f(x)=x2-4x+6=(x-2)2+2,因为x∈[1,5),如图所示,所以函数f(x)的值域为[2,11).
求函数值域的常用方法
1.配方法:此方法是求“二次函数类”值域的基本方法,即把函数通过配方转化为能直接看出其值域的函数的方法.
2.图象法:通过画出函数的图象,由图形的直观性获得函数的值域.
3.分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域.
方法技巧
要使函数有意义,则x+2≠0,解得x≠-2,
所以函数f(x)的定义域是{x|x≠-2}.
索引
高考链接
当堂训练
(15分钟)(满分20分)
请同学们完成当堂训练的题目
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
