2023—2024学年华东师大版数学九年级上册 第22章 一元二次方程 单元测试(含答案)
文档属性
| 名称 | 2023—2024学年华东师大版数学九年级上册 第22章 一元二次方程 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-28 19:07:48 | ||
图片预览


文档简介
第22章 一元二次方程单元测试
一、单选题(每小题3分,共30分)
1.下列方程中,关于的一元二次方程是( )
A. B. C. D.
2.一元二次方程的二次项系数、一次项系数、常数项分别是( )
A.3,5,1 B.3,1,5 C.3,,1 D.3,1,
3.下列一元二次方程中没有实数根的是( )
A. B. C. D.
4.若关于x的一元二次方程有一个根为,则k的值为( )
A. B.3 C. D.9
5.用配方法解一元二次方程,配方后得到的方程是( )
A. B. C. D.
6.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了,另一边减少了2,剩余空地的面积为18,求原正方形空地的边长,设原正方形的空地的边长为,则可列方程为( )
A. B. C. D.
7.对于实数,定义运算“☆”如下:,例如,则方程的根的情况为( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
8.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.且 C. D.且
9.如图,在中,,点M从点A出发沿边向点B以的速度移动,点N从点B出发沿边向点C以的速度移动.当一个点先到达终点时,另一个点也停止运动,当的面积为时,点M,N的运动时间为( )
A. B. C. D.
10.若,则等于( )
A.2023 B.2022 C.2021 D.2020
二、填空题(每小题3分,共30分)
11.若是关于x的一元二次方程,则 .
12.春季流感病毒传播速度快,我们要做好预防.如果有一个人患了流感,经过两轮传染后共有256人患了流感,则每轮传染中平均一个人传染了 人.
13.若最简二次根式与是同类二次根式,则 .
14.若关于x的一元二次方程和有公共根,则a的值是_____________.
15.若,则 .
16.已知,是一元二次方程的两个根,则的值等于 .
17.已知等腰三角形的一边长,另外两边的长恰好是关于的一元二次方程的两个根,则的周长为
18.如图,在一块长为22米,宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米,则道路的宽为 米.
19.已知方程的一个根为,则的值为
20.设一元二次方程的两根分别为a,b,根据一元二次方程根与系数的关系可知:,记,那么 .
三、解答题(每小题8分,共40分)
21.解方程:
(1)(2x﹣1)2=25; (2)x2﹣2x﹣1=0;
(3)2x2﹣6x+5=0; (4)(2x﹣3)2=5(2x﹣3).
22.若关于x的一元二次方程有两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出的值;若不存在,说明理由.
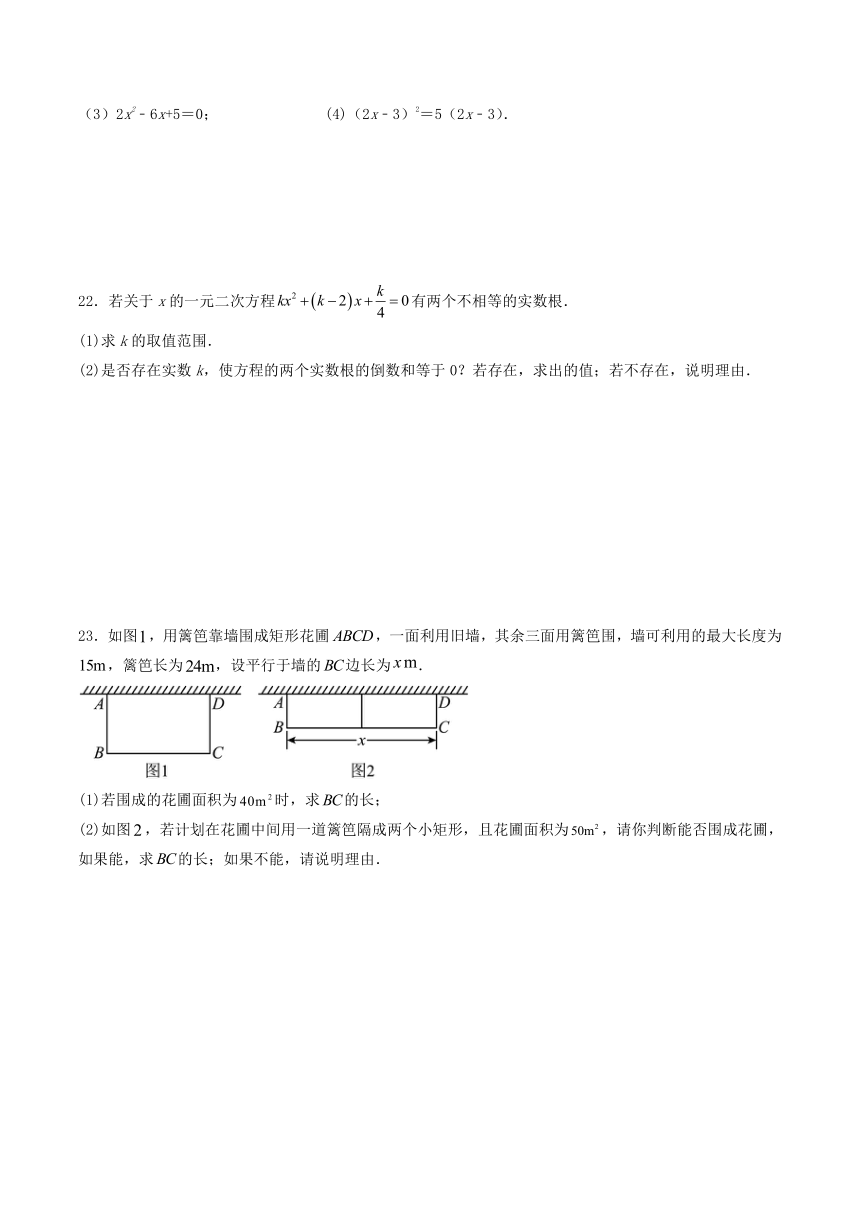
23.如图,用篱笆靠墙围成矩形花圃,一面利用旧墙,其余三面用篱笆围,墙可利用的最大长度为,篱笆长为,设平行于墙的边长为.
(1)若围成的花圃面积为时,求的长;
(2)如图,若计划在花圃中间用一道篱笆隔成两个小矩形,且花圃面积为,请你判断能否围成花圃,如果能,求的长;如果不能,请说明理由.
24.因粤港澳大湾区和中国特色社会主义先行示范区的双重利好,深圳已成为国内外游客最喜欢的旅游目的地城市之一,深圳著名旅游“网红打卡地”东部华侨城景区在2020年春节长假期间,共接待游客达20万人次,预计在2022年春节长假期间,将接待游客达万人次.
(1)求东部华侨城景区2020至2022年春节长假期间接待游客人次的平均增长率.
(2)东部华侨城景区一奶茶店销售一款奶茶,每杯成本价为6元,根据销售经验,在旅游旺季,若每杯定价25元,则平均每天可销售300杯,若每杯价格降低1元,则平均每天可多销售30杯,2022年春节期间,店家决定进行降价促销活动,则当每杯售价定为多少元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额?
25.阅读材料,并完成下列问题:
不难求得方程的解是,;
的解是,;
的解是,;
(1)观察上述方程及其解,可猜想关于x的方程的解是 ;
(2)试用“求出关于x的方程的解”的方法证明你的猜想;
(3)利用你猜想的结论,解关于的方程.
参考答案
1.C 2.C 3.C 4.A 5.B 6.A 7.C 8.B 9.B 10.A
11. 12.15 13. 14.2 15. 16. 17.15 18.2 19.2022 20.100
21.【详解】解:(1)∵(2x-1)2=25,
∴2x-1=5或2x-1=-5,
解得x1=3,x2=-2;
(2)∵x2-2x-1=0,
∴x2-2x=1,
∴x2-2x+1=1+1,即(x-1)2=2,
∴x-1=或x-1=-,
解得x1=1+,x2=1-;
(3)2x2﹣6x+5=0,
∵a=2,b=-6,c=5,
∴△=(-6)2-4×2×5=-4<0,
∴原方程没有实数根;
(4)(2x﹣3)2=5(2x﹣3),
∴(2x﹣3)2-5(2x﹣3)=0,
∴(2x -3)(2x-3-5)=0,
则2x-3=0或2x-8=0,
解得x1=,x2=4.
22.【详解】(1)∵一元二次方程有两个不相等的实数根
∴,
解得且
(2)假设存在实数k,使方程两实数根的倒数和为0
设方程的两根为 .则
∴
即,且
解得
又∵
∴不存在实数k,使方程两实数根的倒数和为0
23.【详解】(1)解:根据题意得,
,
则,
∴,
因为,
所以舍去,
所以,
答:的长为米;
(2)解:不能围成花圃,理由如下:
根据题意得,
,
方程可化为,
∴,
∴方程无实数解,
∴不能围成花圃;
24.【详解】(1)解:设年平均增长率为x,由题意得:
,
解得:,(舍).
答:年平均增长率为.
(2)解:设当每杯售价定为y元时,店家在此款奶茶实现平均每天6300元的利润额,由题意得:
,
整理得:,
解得:,.
∵售价不超过20元,
∴.
答:当每杯售价定为20元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额.
25.【详解】(1)解:观察以上方程可得方程的解,
,,
检验:,
,,
原方程的解为,;
故答案:,.
(2)解:方程两边同时乘以得
,
整理得:,
,
解得:,;
检验:,
,,
原方程的解为,.
(3)解:,
,
,
,
,,
,,
检验:由原方程得:,,
,,
原方程的解为,.
一、单选题(每小题3分,共30分)
1.下列方程中,关于的一元二次方程是( )
A. B. C. D.
2.一元二次方程的二次项系数、一次项系数、常数项分别是( )
A.3,5,1 B.3,1,5 C.3,,1 D.3,1,
3.下列一元二次方程中没有实数根的是( )
A. B. C. D.
4.若关于x的一元二次方程有一个根为,则k的值为( )
A. B.3 C. D.9
5.用配方法解一元二次方程,配方后得到的方程是( )
A. B. C. D.
6.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图阴影部分),原空地一边减少了,另一边减少了2,剩余空地的面积为18,求原正方形空地的边长,设原正方形的空地的边长为,则可列方程为( )
A. B. C. D.
7.对于实数,定义运算“☆”如下:,例如,则方程的根的情况为( )
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
8.若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是( )
A. B.且 C. D.且
9.如图,在中,,点M从点A出发沿边向点B以的速度移动,点N从点B出发沿边向点C以的速度移动.当一个点先到达终点时,另一个点也停止运动,当的面积为时,点M,N的运动时间为( )
A. B. C. D.
10.若,则等于( )
A.2023 B.2022 C.2021 D.2020
二、填空题(每小题3分,共30分)
11.若是关于x的一元二次方程,则 .
12.春季流感病毒传播速度快,我们要做好预防.如果有一个人患了流感,经过两轮传染后共有256人患了流感,则每轮传染中平均一个人传染了 人.
13.若最简二次根式与是同类二次根式,则 .
14.若关于x的一元二次方程和有公共根,则a的值是_____________.
15.若,则 .
16.已知,是一元二次方程的两个根,则的值等于 .
17.已知等腰三角形的一边长,另外两边的长恰好是关于的一元二次方程的两个根,则的周长为
18.如图,在一块长为22米,宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米,则道路的宽为 米.
19.已知方程的一个根为,则的值为
20.设一元二次方程的两根分别为a,b,根据一元二次方程根与系数的关系可知:,记,那么 .
三、解答题(每小题8分,共40分)
21.解方程:
(1)(2x﹣1)2=25; (2)x2﹣2x﹣1=0;
(3)2x2﹣6x+5=0; (4)(2x﹣3)2=5(2x﹣3).
22.若关于x的一元二次方程有两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出的值;若不存在,说明理由.
23.如图,用篱笆靠墙围成矩形花圃,一面利用旧墙,其余三面用篱笆围,墙可利用的最大长度为,篱笆长为,设平行于墙的边长为.
(1)若围成的花圃面积为时,求的长;
(2)如图,若计划在花圃中间用一道篱笆隔成两个小矩形,且花圃面积为,请你判断能否围成花圃,如果能,求的长;如果不能,请说明理由.
24.因粤港澳大湾区和中国特色社会主义先行示范区的双重利好,深圳已成为国内外游客最喜欢的旅游目的地城市之一,深圳著名旅游“网红打卡地”东部华侨城景区在2020年春节长假期间,共接待游客达20万人次,预计在2022年春节长假期间,将接待游客达万人次.
(1)求东部华侨城景区2020至2022年春节长假期间接待游客人次的平均增长率.
(2)东部华侨城景区一奶茶店销售一款奶茶,每杯成本价为6元,根据销售经验,在旅游旺季,若每杯定价25元,则平均每天可销售300杯,若每杯价格降低1元,则平均每天可多销售30杯,2022年春节期间,店家决定进行降价促销活动,则当每杯售价定为多少元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额?
25.阅读材料,并完成下列问题:
不难求得方程的解是,;
的解是,;
的解是,;
(1)观察上述方程及其解,可猜想关于x的方程的解是 ;
(2)试用“求出关于x的方程的解”的方法证明你的猜想;
(3)利用你猜想的结论,解关于的方程.
参考答案
1.C 2.C 3.C 4.A 5.B 6.A 7.C 8.B 9.B 10.A
11. 12.15 13. 14.2 15. 16. 17.15 18.2 19.2022 20.100
21.【详解】解:(1)∵(2x-1)2=25,
∴2x-1=5或2x-1=-5,
解得x1=3,x2=-2;
(2)∵x2-2x-1=0,
∴x2-2x=1,
∴x2-2x+1=1+1,即(x-1)2=2,
∴x-1=或x-1=-,
解得x1=1+,x2=1-;
(3)2x2﹣6x+5=0,
∵a=2,b=-6,c=5,
∴△=(-6)2-4×2×5=-4<0,
∴原方程没有实数根;
(4)(2x﹣3)2=5(2x﹣3),
∴(2x﹣3)2-5(2x﹣3)=0,
∴(2x -3)(2x-3-5)=0,
则2x-3=0或2x-8=0,
解得x1=,x2=4.
22.【详解】(1)∵一元二次方程有两个不相等的实数根
∴,
解得且
(2)假设存在实数k,使方程两实数根的倒数和为0
设方程的两根为 .则
∴
即,且
解得
又∵
∴不存在实数k,使方程两实数根的倒数和为0
23.【详解】(1)解:根据题意得,
,
则,
∴,
因为,
所以舍去,
所以,
答:的长为米;
(2)解:不能围成花圃,理由如下:
根据题意得,
,
方程可化为,
∴,
∴方程无实数解,
∴不能围成花圃;
24.【详解】(1)解:设年平均增长率为x,由题意得:
,
解得:,(舍).
答:年平均增长率为.
(2)解:设当每杯售价定为y元时,店家在此款奶茶实现平均每天6300元的利润额,由题意得:
,
整理得:,
解得:,.
∵售价不超过20元,
∴.
答:当每杯售价定为20元时,既能让顾客获得最大优惠,又可让店家在此款奶茶实现平均每天6300元的利润额.
25.【详解】(1)解:观察以上方程可得方程的解,
,,
检验:,
,,
原方程的解为,;
故答案:,.
(2)解:方程两边同时乘以得
,
整理得:,
,
解得:,;
检验:,
,,
原方程的解为,.
(3)解:,
,
,
,
,,
,,
检验:由原方程得:,,
,,
原方程的解为,.
