2023—2024学年人教版数学九年级上册 22.3实际问题与二次函数 同步练习 (无答案)
文档属性
| 名称 | 2023—2024学年人教版数学九年级上册 22.3实际问题与二次函数 同步练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-28 19:00:28 | ||
图片预览

文档简介
22.3实际问题与二次函数 同步练习
一、单选题
1.下列两个量之间的关系不属于二次函数的是( )
A.速度一定时,汽车行使的路程与时间的关系
B.质量一定时,物体具有的动能和速度的关系
C.质量一定时,运动的物体所受到的阻力与运动速度的关系
D.从高空自由降落的物体,下降的高度与下降的时间的关系
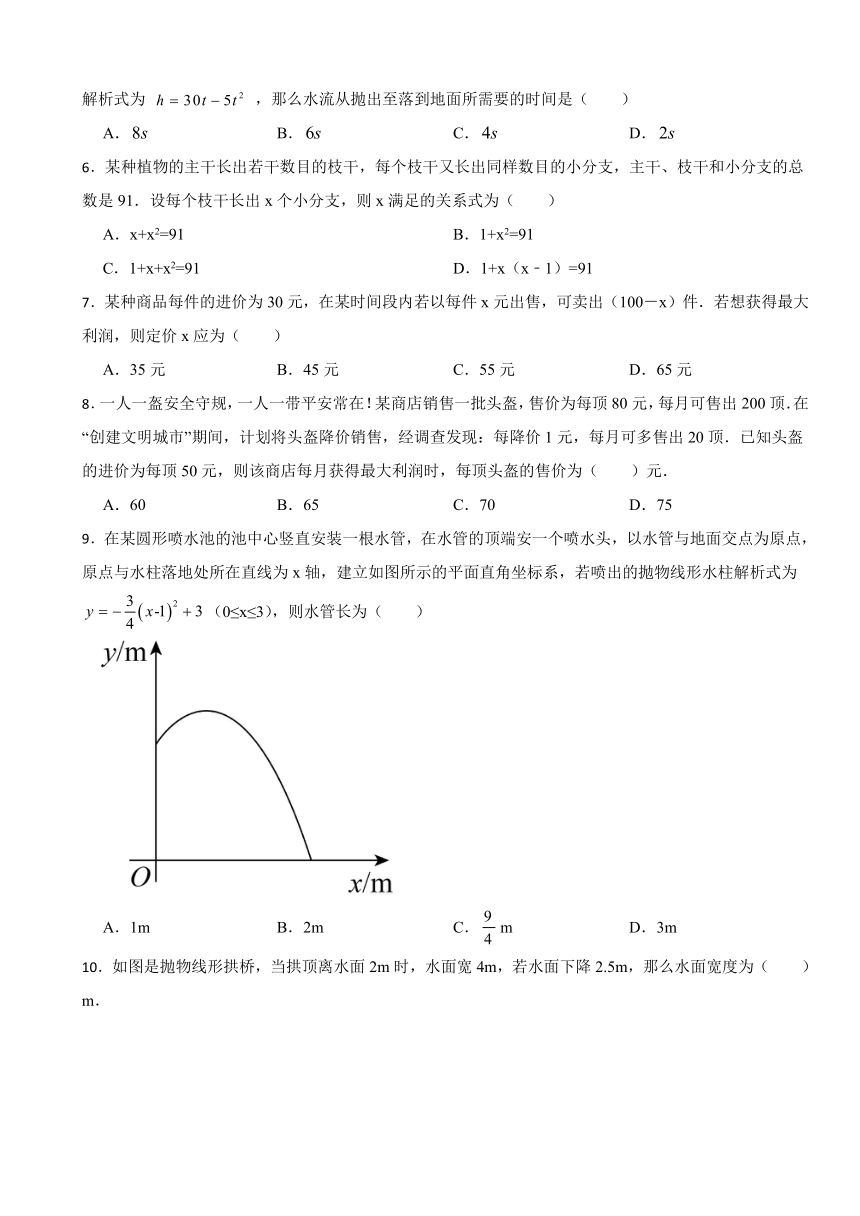
2.如图,小姚身高m在某次投篮中,球的运动路线是抛物线y=﹣x2+的一部分,若命中篮圈中心,则他与篮底的距离是( )
A.3.5m B.4m C.4.5m D.4.6m
3.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y=-x2+50x B.y=x2-50x C.y=-x2+25x D.y=-2x2+25
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t= ;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③ B.①②③ C.①②③④ D.②③④
5.某公园有一个圆形喷水池,喷出的水流呈抛物线状,一条水流的高度 与水流时间 之间的解析式为 ,那么水流从抛出至落到地面所需要的时间是( )
A. B. C. D.
6.某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是91.设每个枝干长出x个小分支,则x满足的关系式为( )
A.x+x2=91 B.1+x2=91
C.1+x+x2=91 D.1+x(x﹣1)=91
7.某种商品每件的进价为30元,在某时间段内若以每件x元出售,可卖出(100-x)件.若想获得最大利润,则定价x应为( )
A.35元 B.45元 C.55元 D.65元
8.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
9.在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A.1m B.2m C.m D.3m
10.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,若水面下降2.5m,那么水面宽度为( )m.
A.3 B.6 C.8 D.9
二、填空题
11.某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .
12.用一根长为20cm的铁丝围成一个长方形,若该长方形的一边长为xcm,面积为ycm2,则y与x之间的关系式为 .
13.受供求关系影响,去年猪肉价格经过连续两轮涨价,价格从40元/千克涨到90元/千克,若两轮涨价的百分率相同,则这个百分率是 .
14.如图,有长为 米的篱笆,一边利用墙(墙的最大可用长度为 米),当花圃的宽 为 米时,围成的花圃面积最大,最大面积为 平方米.
15.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是 m.
三、解答题
16.为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.
17.某商场购进一批单价为40元的商品,若按每件50元销售,平均每天可销售90件.市场调查发现,这种商品的销售单价每提高1元,平均每天少销售3件.将销售单价定为多少,才能使每天所获销售利润W最大?最大利润W是多少?
18.如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=﹣x2+x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
(1)飞行的水平距离是多少时,球最高?
(2)球从飞出到落地的水平距离是多少?
19.为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每吨涨1千元,每天销量将减少2吨,每吨平均投入成本2千元,为了抢占市场,该村产业合作社决定,批发价每吨不低于4千元
(1)求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?
20.如图,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y=﹣ x2+4.保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少.
21.如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,过直线AC上一点G作y轴的平行线交抛物线一点F,是否存在点F,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
一、单选题
1.下列两个量之间的关系不属于二次函数的是( )
A.速度一定时,汽车行使的路程与时间的关系
B.质量一定时,物体具有的动能和速度的关系
C.质量一定时,运动的物体所受到的阻力与运动速度的关系
D.从高空自由降落的物体,下降的高度与下降的时间的关系
2.如图,小姚身高m在某次投篮中,球的运动路线是抛物线y=﹣x2+的一部分,若命中篮圈中心,则他与篮底的距离是( )
A.3.5m B.4m C.4.5m D.4.6m
3.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y=-x2+50x B.y=x2-50x C.y=-x2+25x D.y=-2x2+25
4.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t= ;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③ B.①②③ C.①②③④ D.②③④
5.某公园有一个圆形喷水池,喷出的水流呈抛物线状,一条水流的高度 与水流时间 之间的解析式为 ,那么水流从抛出至落到地面所需要的时间是( )
A. B. C. D.
6.某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是91.设每个枝干长出x个小分支,则x满足的关系式为( )
A.x+x2=91 B.1+x2=91
C.1+x+x2=91 D.1+x(x﹣1)=91
7.某种商品每件的进价为30元,在某时间段内若以每件x元出售,可卖出(100-x)件.若想获得最大利润,则定价x应为( )
A.35元 B.45元 C.55元 D.65元
8.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
9.在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A.1m B.2m C.m D.3m
10.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,若水面下降2.5m,那么水面宽度为( )m.
A.3 B.6 C.8 D.9
二、填空题
11.某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .
12.用一根长为20cm的铁丝围成一个长方形,若该长方形的一边长为xcm,面积为ycm2,则y与x之间的关系式为 .
13.受供求关系影响,去年猪肉价格经过连续两轮涨价,价格从40元/千克涨到90元/千克,若两轮涨价的百分率相同,则这个百分率是 .
14.如图,有长为 米的篱笆,一边利用墙(墙的最大可用长度为 米),当花圃的宽 为 米时,围成的花圃面积最大,最大面积为 平方米.
15.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是 m.
三、解答题
16.为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.
17.某商场购进一批单价为40元的商品,若按每件50元销售,平均每天可销售90件.市场调查发现,这种商品的销售单价每提高1元,平均每天少销售3件.将销售单价定为多少,才能使每天所获销售利润W最大?最大利润W是多少?
18.如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=﹣x2+x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
(1)飞行的水平距离是多少时,球最高?
(2)球从飞出到落地的水平距离是多少?
19.为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每吨涨1千元,每天销量将减少2吨,每吨平均投入成本2千元,为了抢占市场,该村产业合作社决定,批发价每吨不低于4千元
(1)求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?
20.如图,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y=﹣ x2+4.保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少.
21.如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,过直线AC上一点G作y轴的平行线交抛物线一点F,是否存在点F,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
同课章节目录
