2.2基本不等式 课件(共20张PPT)
文档属性
| 名称 | 2.2基本不等式 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第一章 统计案例
2.2
基 本 不 等 式
学习目标
1.掌握基本不等式及其推导过程.
2.能用基本不等式解决简单的最值问题.
3.能够运用基本不等式解决生活中的应用问题.
4.在猜想论证的过程中,体会数学的严谨性
问题 试比较a2+b2与2ab的大小关系?
解:
当且仅当a=b时,等号成立
PART 重要不等式
当且仅当a=b时,等号成立
文字表述:两个实数的平方和大于等于它们乘积的2倍
重要不等式
上节课我们利用面积法和完全平方公式得出了重要不等式:
,有:
当且仅当时,等号成立.
基本不等式
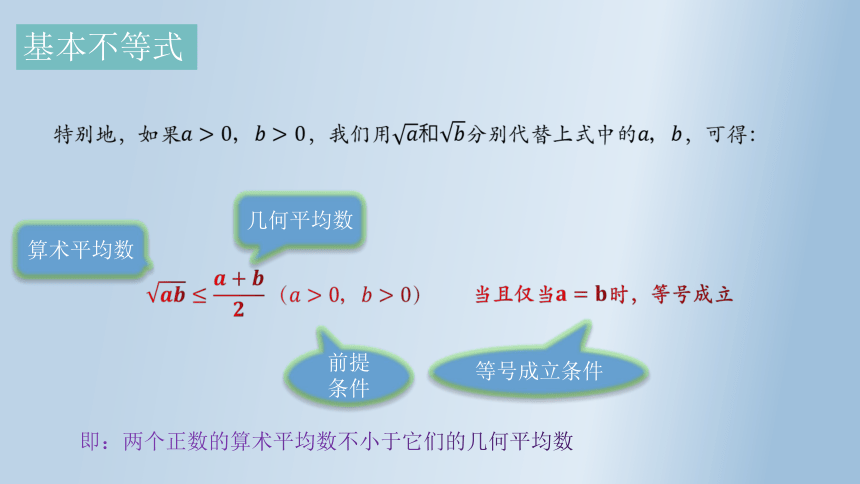
特别地,如果,我们用分别代替上式中的,可得:
当且仅当时,等号成立
等号成立条件
算术平均数
几何平均数
前提
条件
即:两个正数的算术平均数不小于它们的几何平均数
证明:要证明 ,
只需证明 ,
所以原不等式成立.
只需证 ,
只要证
而 显然成立.
过程:执果索因
分析法
新知探究
分析法
新知探索
在图中,是圆的直径,点是上一点,过点作垂直于的弦,连接你能利用这个图形,得出基本不等式的几何解释吗?
如图,可证 因而
由于小于或等于圆的半径,用不等式表示为.
显然,当且仅当点与圆心重合,即当时,上述不等式的等号成立.
基本不等式的前提条件
在问题“已知x>0,求 x + 的最小值”的解决过程中不难发现:最小值是一个常数2,并且只能在x=1时取到. 换一句话说:如果x<0,或x>2等等,x + 的最小值就不是2或者不存在.
由此我们归纳,依a+b≥2 求两个数和或积的最值,
必须要满足条件:(1) ;
(2) ;
(3) .
1.已知x,y都是正数,求证:
(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值2;
(2)如果和x+y等于定值S,那么当x=y时,积xy有最大值S2.
方
法
总结
核心素养 之 逻辑推理 + 数学建模
问
题
分
析
提示:因为x,y都是正数,所以x+y ≥2.
无论是“和”定还是“积”定,不等号的另一侧部分将会取得最
值,且都在x=y时取得等号.
基本不等式从一侧到另一侧,本质上是一种放大或缩小;当一侧为定值时,即为另一侧的一最值;当然,要满足取等的条件.
2.已知a,b都是正数,求证:
(1) ≤; (2)≤.
方
法
总结
核心素养 之 逻辑推理 + 数学运算
问
题
分
析
提示:(1) ≥2
(2) )2=≤.
不等式证明过程中,可以先局部使用基本不等式放缩,再整体观察化归; 也可以先两边平方或开方,再用基本不等式.
3.某企业要建造一个容积为18cm3,深为2m的长方体形无盖贮水池,如果池底和池壁每平方米的造价分别为200元和150元,怎样设计该水池可使得总造价最低?最低总造价为多少?
方
法
总结
核心素养 之 数学抽象 + 数学建模
问
题
分
析
设贮水池池底长和宽分别为xm,ym,水池总造价为z元,则由容积为18m3, 可得2xy=18, 因此xy=9,
z=200×9+150(2×2x+2×2y)=1800+600(x+y)
≥1800+600×2=5400 当x=y=3时,等号成立.
目标函数中出现两个正变量的和,则依据基本不等式可得其最小值,最后要确认取等条件成立.
【例题】用篱笆围成一个面积为100平方米的矩形菜园,当这个矩形的边长为多少时,所用的篱笆最少,最短长度是多少?
【解】由题意设篱笆的长和宽分别为米,且
所以米
当且仅当米,即围成正方形时,有最短长度40米
基本不等式的实际应用
【例题】用一段长为36米的铁丝网围成一个矩形菜园,当这个矩形的长和宽各为多少时,菜园的面积最大?最大面积是多少?
【解】由题意设篱笆的长和宽分别为米,且
所以为平方米,根据基本不等式,
,即
当且仅当,即围成正方形时,有最大面积81平方米.
基本不等式的实际应用
【例题】某工厂要建造一个长方体形状的无盖蓄水池,其容积为4800立方米,深为3米.如果池底每平方米的造价为150元,池壁每平方米的造价为120元,那么怎样设计水池才能使总造价最低?最低造价是多少?
【解】设水池底面的长和宽分别为米,且,总造价元,
根据题意,有
因为容积为,所以,,
当且仅当米时,取得最低总造价
元
,
基本不等式的实际应用
基本不等式
利用基本不等式求最值的条件:
一正、二定、三相等。
基本不等式
基本不等式
3.已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
证明:所以
(1)等于定值P时, ,∴
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,
当且仅当时,上式等号成立,此时有最大值
课堂小结
课堂小结:
(1)重要不等式;
(2)基本不等式.
谢谢大家
We have many PowerPoint templates that has been specifically designed to help anyone that is stepping into the world of PowerPt for the very first time.
第一章 统计案例
2.2
基 本 不 等 式
学习目标
1.掌握基本不等式及其推导过程.
2.能用基本不等式解决简单的最值问题.
3.能够运用基本不等式解决生活中的应用问题.
4.在猜想论证的过程中,体会数学的严谨性
问题 试比较a2+b2与2ab的大小关系?
解:
当且仅当a=b时,等号成立
PART 重要不等式
当且仅当a=b时,等号成立
文字表述:两个实数的平方和大于等于它们乘积的2倍
重要不等式
上节课我们利用面积法和完全平方公式得出了重要不等式:
,有:
当且仅当时,等号成立.
基本不等式
特别地,如果,我们用分别代替上式中的,可得:
当且仅当时,等号成立
等号成立条件
算术平均数
几何平均数
前提
条件
即:两个正数的算术平均数不小于它们的几何平均数
证明:要证明 ,
只需证明 ,
所以原不等式成立.
只需证 ,
只要证
而 显然成立.
过程:执果索因
分析法
新知探究
分析法
新知探索
在图中,是圆的直径,点是上一点,过点作垂直于的弦,连接你能利用这个图形,得出基本不等式的几何解释吗?
如图,可证 因而
由于小于或等于圆的半径,用不等式表示为.
显然,当且仅当点与圆心重合,即当时,上述不等式的等号成立.
基本不等式的前提条件
在问题“已知x>0,求 x + 的最小值”的解决过程中不难发现:最小值是一个常数2,并且只能在x=1时取到. 换一句话说:如果x<0,或x>2等等,x + 的最小值就不是2或者不存在.
由此我们归纳,依a+b≥2 求两个数和或积的最值,
必须要满足条件:(1) ;
(2) ;
(3) .
1.已知x,y都是正数,求证:
(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值2;
(2)如果和x+y等于定值S,那么当x=y时,积xy有最大值S2.
方
法
总结
核心素养 之 逻辑推理 + 数学建模
问
题
分
析
提示:因为x,y都是正数,所以x+y ≥2.
无论是“和”定还是“积”定,不等号的另一侧部分将会取得最
值,且都在x=y时取得等号.
基本不等式从一侧到另一侧,本质上是一种放大或缩小;当一侧为定值时,即为另一侧的一最值;当然,要满足取等的条件.
2.已知a,b都是正数,求证:
(1) ≤; (2)≤.
方
法
总结
核心素养 之 逻辑推理 + 数学运算
问
题
分
析
提示:(1) ≥2
(2) )2=≤.
不等式证明过程中,可以先局部使用基本不等式放缩,再整体观察化归; 也可以先两边平方或开方,再用基本不等式.
3.某企业要建造一个容积为18cm3,深为2m的长方体形无盖贮水池,如果池底和池壁每平方米的造价分别为200元和150元,怎样设计该水池可使得总造价最低?最低总造价为多少?
方
法
总结
核心素养 之 数学抽象 + 数学建模
问
题
分
析
设贮水池池底长和宽分别为xm,ym,水池总造价为z元,则由容积为18m3, 可得2xy=18, 因此xy=9,
z=200×9+150(2×2x+2×2y)=1800+600(x+y)
≥1800+600×2=5400 当x=y=3时,等号成立.
目标函数中出现两个正变量的和,则依据基本不等式可得其最小值,最后要确认取等条件成立.
【例题】用篱笆围成一个面积为100平方米的矩形菜园,当这个矩形的边长为多少时,所用的篱笆最少,最短长度是多少?
【解】由题意设篱笆的长和宽分别为米,且
所以米
当且仅当米,即围成正方形时,有最短长度40米
基本不等式的实际应用
【例题】用一段长为36米的铁丝网围成一个矩形菜园,当这个矩形的长和宽各为多少时,菜园的面积最大?最大面积是多少?
【解】由题意设篱笆的长和宽分别为米,且
所以为平方米,根据基本不等式,
,即
当且仅当,即围成正方形时,有最大面积81平方米.
基本不等式的实际应用
【例题】某工厂要建造一个长方体形状的无盖蓄水池,其容积为4800立方米,深为3米.如果池底每平方米的造价为150元,池壁每平方米的造价为120元,那么怎样设计水池才能使总造价最低?最低造价是多少?
【解】设水池底面的长和宽分别为米,且,总造价元,
根据题意,有
因为容积为,所以,,
当且仅当米时,取得最低总造价
元
,
基本不等式的实际应用
基本不等式
利用基本不等式求最值的条件:
一正、二定、三相等。
基本不等式
基本不等式
3.已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
证明:所以
(1)等于定值P时, ,∴
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,
当且仅当时,上式等号成立,此时有最大值
课堂小结
课堂小结:
(1)重要不等式;
(2)基本不等式.
谢谢大家
We have many PowerPoint templates that has been specifically designed to help anyone that is stepping into the world of PowerPt for the very first time.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
