6.2 二次函数的图象和性质课件

课件16张PPT。 二次函数y=2x2向下平移1个单位，再向左移3个单位得到什么函数呢？义务教育课程标准实验教科书二次函数的图像和性质 九年级 （下）————江苏泰兴洋思中学学习目标初 三 数 学 组
1.能归纳y=a(x+h)2 +k的性质.
2.会用配方法确定二次函数图象的
顶点坐标及函数的最值.
3.会运用公式求二次函数的顶点坐
标、最值、对称轴.自学指导一 认真看课本第16页的内容,结合卡通
人的话想一想：
1.y=（x+1)2+2与y=（x+1)2和y=x2的关系是
什么？运用什么方法理解？
2.函数y=a(x+h)2+k可以由我们所学的哪些
函数变形得到？
3.一般式怎样能到顶点式？
5分钟后,比谁能正确小结y=a(x+h)2 +k
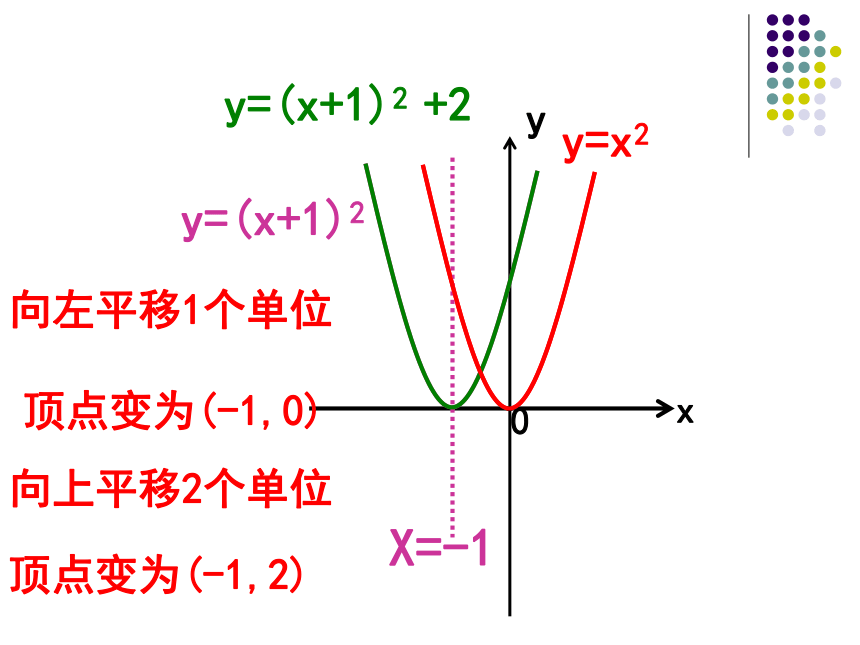
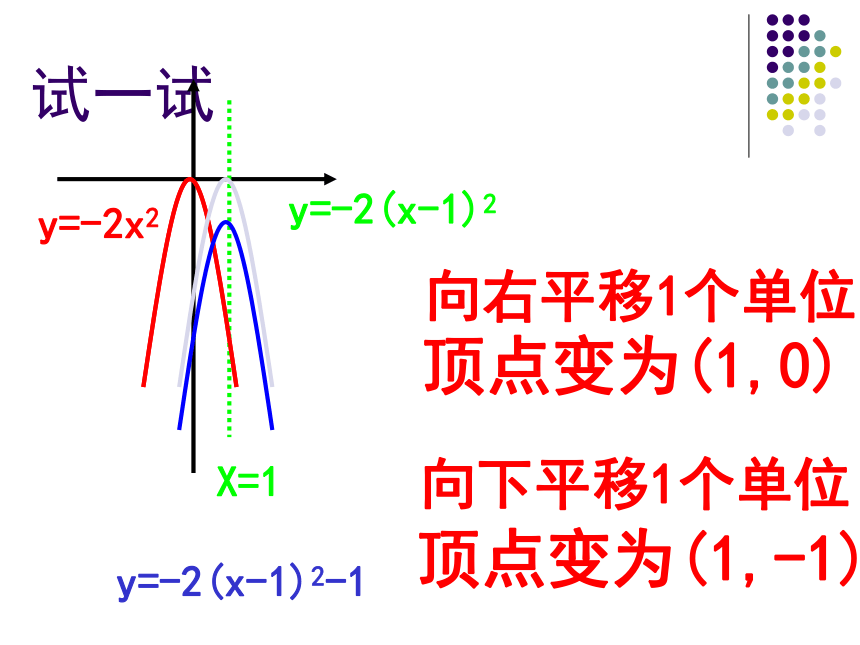
的性质. 通过自学你学到了什么？还有什么疑问？y=x2y=(x+1)2xyX=-10y=(x+1)2 +2向左平移1个单位顶点变为(-1,0)向上平移2个单位顶点变为(-1,2)试一试X=1y=-2x2y=-2(x-1)2y=-2(x-1)2-1向右平移1个单位向下平移1个单位顶点变为(1,0)顶点变为(1,-1)xyX=-10y=(x+1)2 +2(-1,2)X=1xy0(1,-1)y=-2(x-1)2-1二次函数y=a(x+h)2+K的性质
①对称轴:
②顶点:
③增减性质:a>0，
　　　　　　　　
　a<0，
　　　　　　　　
④最值:
　　　
⑤平移:
直线x=-h(-h,K)当x＜-h，y随x增大而减小当x＞-h，y随x增大而增大当x＜-h，y随x增大而增大当x＞-h，y随x增大而减小若a＞０当x=-h时,y最小=K；若a＜０当x=-h时,y最大=K
由y=ax2先向右(h<0)或向左(h>0)平移|h|
个单位,再向上(k+)或向下(k-)平移 |Ｋ|
个单位得y=a(x+h)2+k.
检测练习1一、直接写出下列函数的顶点、最值、对称轴，能说出它们之间的联系。
1、y=（x-2）2 2、y=（x+3）2-2
3、y=2x2 4、y=-（x-4）2-1
5、y=-3x2-3 6、y=-（2x-3）2+1
7、y=-x2-2x+1 2.用公式法求下列抛物线的顶点坐标和对称轴及最值.检测练习1 仔细看P.17例题内容，要求：
1.弄清例题中求最值的方法.
2.弄清二次函数一般式化顶点式的方法.
3.探究函数y=ax2+bx+c(a≠0)的性质.
4分钟后，比谁能运用公式求函数的顶
点及最值.自学指导二 已知二次函数y=x2+2x+3 (1)当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？（2）若一直线经过原点且经过二次函数y=x2+2x+3的顶点，求这条直线的解析式.检测题2 当实数m变化时，抛物线y=mx2+2x+3
的顶点P，在哪个函数图象上？请写出来.拓展延伸课 堂 作 业必做题: 教材 P.20 习题 T7、8
选做题:
1.将二次函数y=- (x-3)2+2沿x轴方向平移 个单位经过
点(2,-1)
2. 二次函数的图象顶点为(4,-8),它与x轴的交点为(6,0).求
该二次函数的解析式.
思考题:
已知:抛物线 y=(x-1)2-4,若设它与x轴的交点为 A、B（A左
B右），与y轴交于点C,顶点为D，求四边形ABDC的面积.
已知抛物线y=-2(x+1)2+k在 x轴上截得的线段长为4.（1）求k的值.（2）若抛物线的顶点为P，与x轴的两交点分别为A、B，求△PAB外接圆的半径.