2023-2024学年人教版数学八年级上册 11.1.1三角形的边课件 (共23张PPT)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册 11.1.1三角形的边课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-28 21:04:13 | ||
图片预览







文档简介
(共23张PPT)
11.1.1三角形的边
11.1与三角形有关的线段
梦里能达到的地方,总有一天,脚步也能达到
人教版八年级数学上册
金字塔—埃及
三角形
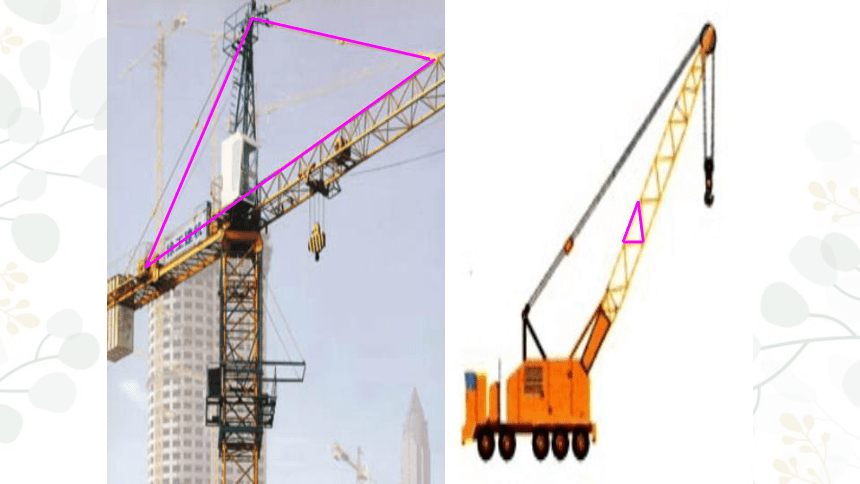
生活中有许多使用三角形的实例.你能从下图中找出三角形吗?
梦里能达到的地方,总有一天,脚步也能达到
梦里能达到的地方,总有一天,脚步也能达到
梦里能达到的地方,总有一天,脚步也能达到
问题1:三角形的边是三条线段,那么任意三条线段能否组成一个三角形呢?
问题2.三条线段应具备什么条件才能构成三角形呢?
探究
首尾顺次相接
位置:
数量:?
不一定
梦里能达到的地方,总有一天,脚步也能达到
如图:在 ABC中,假设有一只小虫要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
路线1:由点B到点C,
路线2:先由点B到点A,再由点A到点C,
即:AB + AC
即:BC
A
B
C
AB + AC
BC
>
____
思考:
结论1:
三角形两边之和大于第三边
(两点之间,线段最短)
同理,我们还可以得到:AB + BC > AC
AC + BC > AB
梦里能达到的地方,总有一天,脚步也能达到
(1)AB + AC > BC
(2)BC+ AC > AB
(3)BC +AB > AC
AB > BC - AC
AC > AB -BC
BC > AC -AB
三角形两边之差小于第三边
结论2:
两边之差<第三边<两边之和
第三边的取值范围:
根据“结论1: ”
三角形两边之和大于第三边
较大的边-较小的边
梦里能达到的地方,总有一天,脚步也能达到
已知三角形一边为5,另一边为3,求第三边长c的取值范围.
解:因为 5-3 < c <5 + 3
所以 2 < c < 8
所以c的取值范围是 2< c <8.
小试牛刀
3-5 < c <5 + 3
梦里能达到的地方,总有一天,脚步也能达到
问题1:三角形的边是三条线段,那么任意三条线段能否组成一个三角形呢?
问题2.三条线段应具备什么条件才能构成三角形呢?
深入探究
首尾顺次相接
位置:
不一定
数量:?
数量:两边之差<第三边<两边之和
梦里能达到的地方,总有一天,脚步也能达到
思考:下列长度的三条线段能否组成三角形?为什么?
(1)1,2,3 (2)2,3,4
深入探究
分析:1+2 =3,
1+3 >2,
2+3 >1;
2-1 < 3,
3-1= 2,
3-2 =1,
因此,以1,2,3无法组成三角形.
分析:2+3 >4,
2+4 >3,
3+4 >2;
3-2 < 4,
4-2 < 3,
4-3 < 2.
因此,以2,3,4可以组成三角形.
因此,判断三条线段能否组成三角形时,只需利用“较短的两边之和大于第三边”就可以进行判断.
三边关系:两边之差<第三边<两边之和
梦里能达到的地方,总有一天,脚步也能达到
知识点: 三角形的三边关系
(1)任意两边之和大于第三边。
(2)任意两边之差小于第三边。
用几何语言表示,如图所示,如果△ABC的三边长分别为a,b,c,则:
①a+b>c,a+c>b,b+c>a;
②I c-a I<b,I c-b I<a,I a-b I<c。
c
b
a
C
B
A
梦里能达到的地方,总有一天,脚步也能达到
例题讲解
1.下列各组线段中,能构成三角形的是( )
A.a=6,b=8,c=15
B.a=7,b=6,c=13
C.a=4,b=5,c=6
D.a=,b=,c=
梦里能达到的地方,总有一天,脚步也能达到
应用练习
2.三角形按边可分为( )
A.等腰三角形、直角三角形、锐角三角形
B.直角三角形、不等边三角形
C.等腰三角形、不等边三角形
D.等腰三角形、等边三角形
梦里能达到的地方,总有一天,脚步也能达到
应用练习
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10
梦里能达到的地方,总有一天,脚步也能达到
应用练习
4.长度为2cm,3cm,4cm和5cm的4根木棒,从中任取三根,可搭成( )种不同的三角形。
梦里能达到的地方,总有一天,脚步也能达到
课堂小结
三角形
相关概念
分类
三边关系
三角形两边的和大于第三边
三角形两边的差小于第三边
梦里能达到的地方,总有一天,脚步也能达到
课堂训练
1.图中有 ______个三角形,用符号表示这些三角形分别为_ __________________________________________________;
其中,以AC为边的三角形有__________________________.
△ABD,△ABE,△ABC,△ADE,△ADC,△AEC
6
△ABC,△ADC,△AEC
梦里能达到的地方,总有一天,脚步也能达到
2.若△ABC三条边的长度分别为m,n,p,且
则这个三角形为( )
A.钝角三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
【解析】根据题意可知m-n=0,n-p=0.所以m=n,n=p,即m=n=p.所以△ABC为等边三角形.故选B.
B
梦里能达到的地方,总有一天,脚步也能达到
3.若三角形的两边长分别是4与2,第三边的长为正整数,则这样的三
角形个数为( )
A.2 B.3 C.4 D.5
B
【解析】设第三边长x,根据三角形的三边关系,得4-2<x<4+2,即2<x<6.因为第三边的长为正整数,所以x可能取3,4,5,则这样的三角形个数为3.故选B.
梦里能达到的地方,总有一天,脚步也能达到
4.(1)已知等腰三角形的一边长为5,一边长为6,求它的周长.
(2)已知等腰三角形的一边长为4,一边长为9,求它的周长.
解:(1)当腰长为5时,底边为6,则周长为5+5+6=16;
当腰长为6时,底边为5,则周长为6+6+5=17.
(2)当腰长为4时,底边为9,4+4<9,不能构成三角形;
当腰长为9时,底边为4,则周长为9+9+4=22.
课堂训练
梦里能达到的地方,总有一天,脚步也能达到
5.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
课堂训练
11.1.1三角形的边
11.1与三角形有关的线段
梦里能达到的地方,总有一天,脚步也能达到
人教版八年级数学上册
金字塔—埃及
三角形
生活中有许多使用三角形的实例.你能从下图中找出三角形吗?
梦里能达到的地方,总有一天,脚步也能达到
梦里能达到的地方,总有一天,脚步也能达到
梦里能达到的地方,总有一天,脚步也能达到
问题1:三角形的边是三条线段,那么任意三条线段能否组成一个三角形呢?
问题2.三条线段应具备什么条件才能构成三角形呢?
探究
首尾顺次相接
位置:
数量:?
不一定
梦里能达到的地方,总有一天,脚步也能达到
如图:在 ABC中,假设有一只小虫要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
路线1:由点B到点C,
路线2:先由点B到点A,再由点A到点C,
即:AB + AC
即:BC
A
B
C
AB + AC
BC
>
____
思考:
结论1:
三角形两边之和大于第三边
(两点之间,线段最短)
同理,我们还可以得到:AB + BC > AC
AC + BC > AB
梦里能达到的地方,总有一天,脚步也能达到
(1)AB + AC > BC
(2)BC+ AC > AB
(3)BC +AB > AC
AB > BC - AC
AC > AB -BC
BC > AC -AB
三角形两边之差小于第三边
结论2:
两边之差<第三边<两边之和
第三边的取值范围:
根据“结论1: ”
三角形两边之和大于第三边
较大的边-较小的边
梦里能达到的地方,总有一天,脚步也能达到
已知三角形一边为5,另一边为3,求第三边长c的取值范围.
解:因为 5-3 < c <5 + 3
所以 2 < c < 8
所以c的取值范围是 2< c <8.
小试牛刀
3-5 < c <5 + 3
梦里能达到的地方,总有一天,脚步也能达到
问题1:三角形的边是三条线段,那么任意三条线段能否组成一个三角形呢?
问题2.三条线段应具备什么条件才能构成三角形呢?
深入探究
首尾顺次相接
位置:
不一定
数量:?
数量:两边之差<第三边<两边之和
梦里能达到的地方,总有一天,脚步也能达到
思考:下列长度的三条线段能否组成三角形?为什么?
(1)1,2,3 (2)2,3,4
深入探究
分析:1+2 =3,
1+3 >2,
2+3 >1;
2-1 < 3,
3-1= 2,
3-2 =1,
因此,以1,2,3无法组成三角形.
分析:2+3 >4,
2+4 >3,
3+4 >2;
3-2 < 4,
4-2 < 3,
4-3 < 2.
因此,以2,3,4可以组成三角形.
因此,判断三条线段能否组成三角形时,只需利用“较短的两边之和大于第三边”就可以进行判断.
三边关系:两边之差<第三边<两边之和
梦里能达到的地方,总有一天,脚步也能达到
知识点: 三角形的三边关系
(1)任意两边之和大于第三边。
(2)任意两边之差小于第三边。
用几何语言表示,如图所示,如果△ABC的三边长分别为a,b,c,则:
①a+b>c,a+c>b,b+c>a;
②I c-a I<b,I c-b I<a,I a-b I<c。
c
b
a
C
B
A
梦里能达到的地方,总有一天,脚步也能达到
例题讲解
1.下列各组线段中,能构成三角形的是( )
A.a=6,b=8,c=15
B.a=7,b=6,c=13
C.a=4,b=5,c=6
D.a=,b=,c=
梦里能达到的地方,总有一天,脚步也能达到
应用练习
2.三角形按边可分为( )
A.等腰三角形、直角三角形、锐角三角形
B.直角三角形、不等边三角形
C.等腰三角形、不等边三角形
D.等腰三角形、等边三角形
梦里能达到的地方,总有一天,脚步也能达到
应用练习
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10
梦里能达到的地方,总有一天,脚步也能达到
应用练习
4.长度为2cm,3cm,4cm和5cm的4根木棒,从中任取三根,可搭成( )种不同的三角形。
梦里能达到的地方,总有一天,脚步也能达到
课堂小结
三角形
相关概念
分类
三边关系
三角形两边的和大于第三边
三角形两边的差小于第三边
梦里能达到的地方,总有一天,脚步也能达到
课堂训练
1.图中有 ______个三角形,用符号表示这些三角形分别为_ __________________________________________________;
其中,以AC为边的三角形有__________________________.
△ABD,△ABE,△ABC,△ADE,△ADC,△AEC
6
△ABC,△ADC,△AEC
梦里能达到的地方,总有一天,脚步也能达到
2.若△ABC三条边的长度分别为m,n,p,且
则这个三角形为( )
A.钝角三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
【解析】根据题意可知m-n=0,n-p=0.所以m=n,n=p,即m=n=p.所以△ABC为等边三角形.故选B.
B
梦里能达到的地方,总有一天,脚步也能达到
3.若三角形的两边长分别是4与2,第三边的长为正整数,则这样的三
角形个数为( )
A.2 B.3 C.4 D.5
B
【解析】设第三边长x,根据三角形的三边关系,得4-2<x<4+2,即2<x<6.因为第三边的长为正整数,所以x可能取3,4,5,则这样的三角形个数为3.故选B.
梦里能达到的地方,总有一天,脚步也能达到
4.(1)已知等腰三角形的一边长为5,一边长为6,求它的周长.
(2)已知等腰三角形的一边长为4,一边长为9,求它的周长.
解:(1)当腰长为5时,底边为6,则周长为5+5+6=16;
当腰长为6时,底边为5,则周长为6+6+5=17.
(2)当腰长为4时,底边为9,4+4<9,不能构成三角形;
当腰长为9时,底边为4,则周长为9+9+4=22.
课堂训练
梦里能达到的地方,总有一天,脚步也能达到
5.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
课堂训练
