12.2 三角形全等的判定一课一练(含解析)
文档属性
| 名称 | 12.2 三角形全等的判定一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 531.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 21:52:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.2 三角形全等的判定一课一练
一、单选题
1.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是: ( )
A.带①去 B.带②去 C.带③去 D.带①和②
2.下列判断正确的是( )
A.有一条直角边对应相等的两个直角三角形全等
B.腰相等的两个等腰三角形全等
C.斜边相等的两个等腰直角三角形全等
D.有一个锐角对应相等的两个直角三角形全等
3.下列方法中,不能判定三角形全等的是 ( )
A.AAA B.SSS C.ASA D.SAS
4.如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )
A.8对 B.4对 C.2对 D.1对
5.如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )
A.30 B.50 C.66 D.80
二、填空题
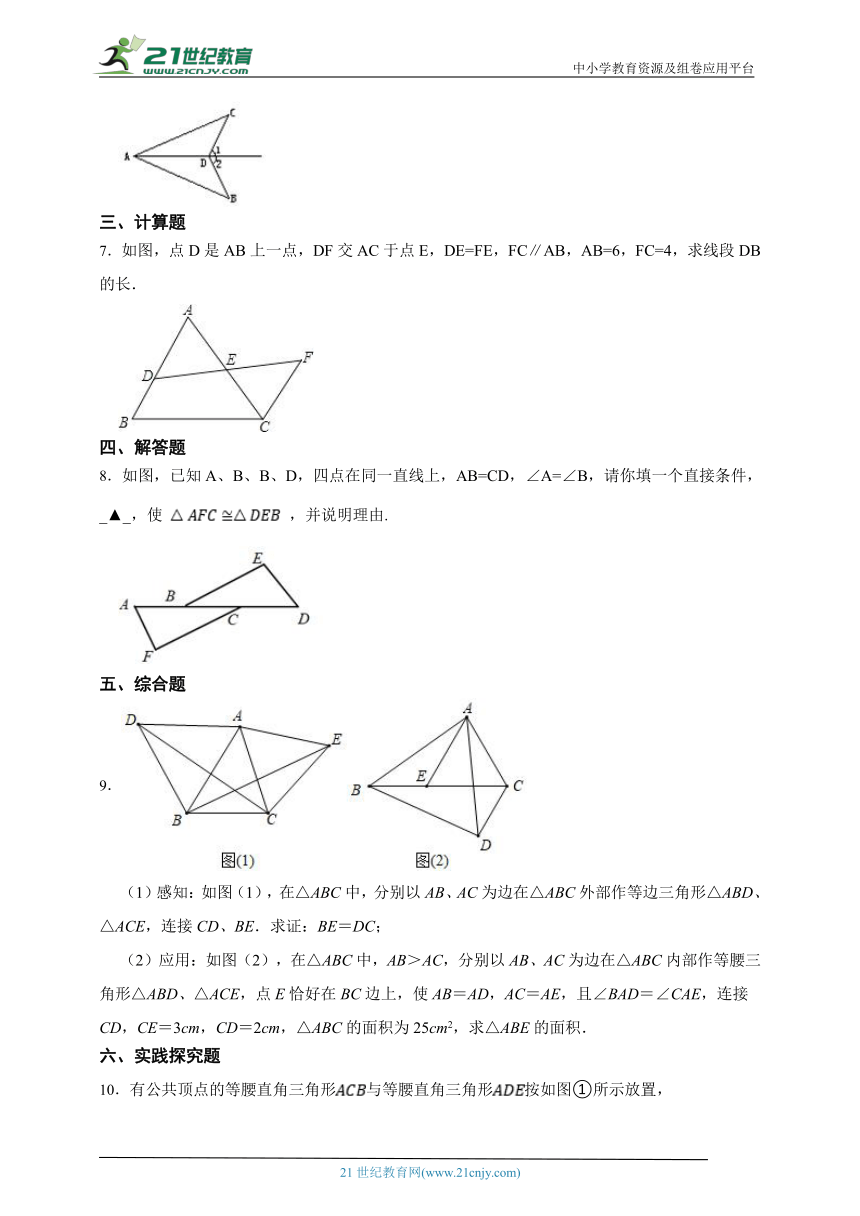
6.如图,∠1=∠2,CD=BD,可证△ABD≌△ACD,则依据是 。
三、计算题
7.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.
四、解答题
8.如图,已知A、B、B、D,四点在同一直线上,AB=CD,∠A=∠B,请你填一个直接条件,_▲_,使 ,并说明理由.
五、综合题
9.
(1)感知:如图(1),在△ABC中,分别以AB、AC为边在△ABC外部作等边三角形△ABD、△ACE,连接CD、BE.求证:BE=DC;
(2)应用:如图(2),在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰三角形△ABD、△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为25cm2,求△ABE的面积.
六、实践探究题
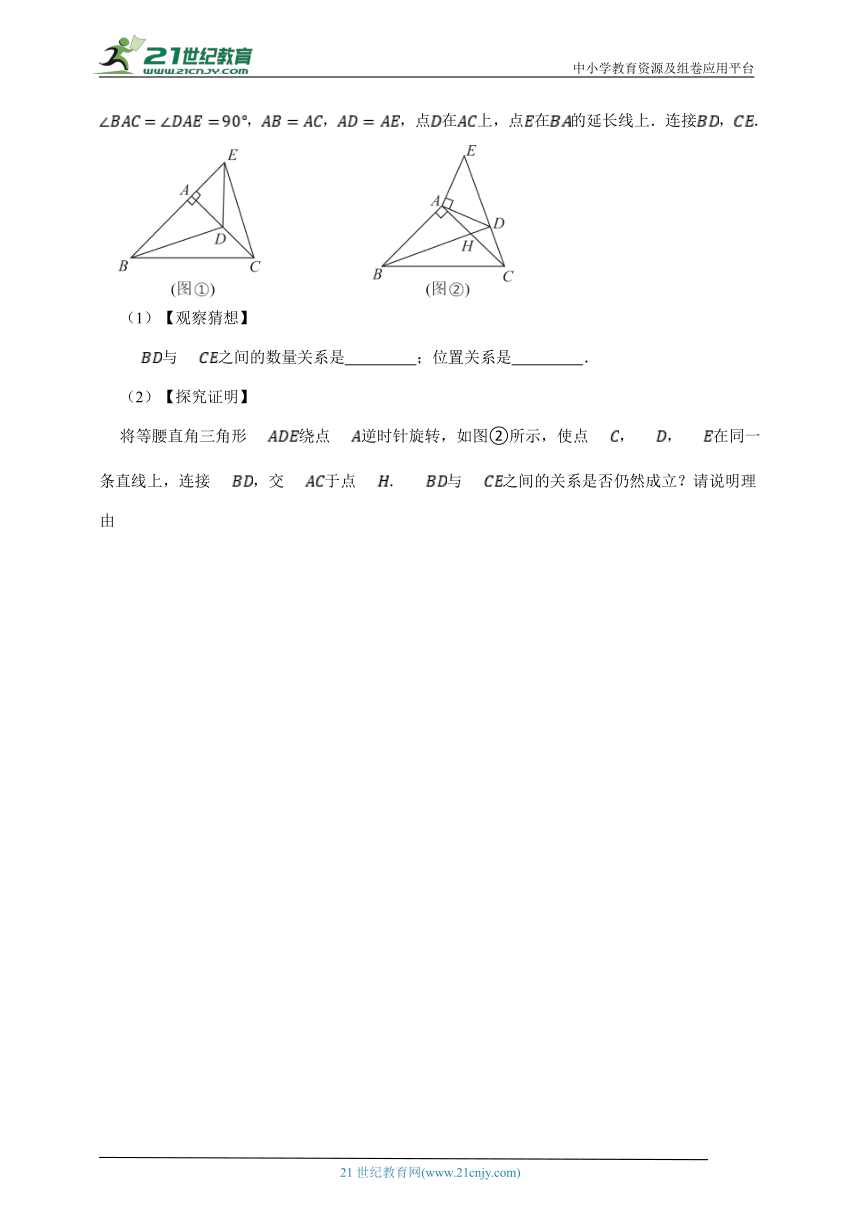
10.有公共顶点的等腰直角三角形与等腰直角三角形按如图①所示放置,,,,点在上,点在的延长线上.连接,.
(1)【观察猜想】
与之间的数量关系是 ;位置关系是 .
(2)【探究证明】
将等腰直角三角形绕点逆时针旋转,如图②所示,使点,,在同一条直线上,连接,交于点.与之间的关系是否仍然成立?请说明理由
答案解析部分
1.【答案】C
【解析】【解答】解:
第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;第二块,仅保留了原三角形的一部分边,所以该块不行;第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定定理,所以应该拿这块去.
故答案为:C.
【分析】有全等三角形的判定可知角边角可以确定,即③可以。
2.【答案】C
【解析】【解答】解:有一条直角边对应相等的两个直角三角形,只知道一边和一角相等,不能判定全等,A不符合题意;
腰相等的两个等腰三角形,只知道两边相等,不能判定全等,B不符合题意;
斜边相等的两个等腰直角三角形,知道三个角和一个边全等,可以通过角角边或角边角判定全等,C符合题意;
D、有一个锐角对应相等的两个直角三角形,只知道三个角相等,不能判定全等,D不符合题意;
故答案为:C
【分析】根据全等三角形的判定方法逐项判断即可。
3.【答案】A
【解析】【解答】解:因为全等三角形的判定定理有“ ”,“ ”,“ ”,“ ”.
三个角相等不等判定三角形全等,只能判定相似.
故答案为:A.
【分析】全等三角形的判定定理有“ ”,“ ”,“ ”,“ ”等判定定理.不符合条件的即我们要找的答案.
4.【答案】B
【解析】【解答】解:∵AB∥CD,AD∥BC,
∴∠CAD=∠ACB,∠BDA=∠DBC,∠BAC=∠DCA,∠ABD=∠CDB,
又∵AC、BD为公共边,
∴△ACD≌△CAB、△BAD≌△DCB(ASA);
∴AD=BC,AB=CD,
∴△AOD≌△COB、△AOB≌△COD(ASA).
所以全等三角形有:△AOD≌△COB、△AOB≌△COD、△ACD≌△CAB、△BAD≌△DCB,共4对;故选B.
【分析】根据AB∥CD,AD∥BC可得到相等的角,再根据公共边AC、BD易证得:△ACD≌△CAB、△BAD≌△DCB(ASA);由上可得AD=BC、AB=CD,再根据平行线确定的角相等可证得:△AOD≌△COB、△AOB≌△COD(ASA).
5.【答案】B
【解析】【解答】∵∠EAO+∠BAH=90°,∠EAO+∠AEO=90°,
∴∠BAH=∠AEO,
∵在△AEO和△BAH中,
,
∴△AEO≌△BAH(AAS),
同理△BCH≌△CDF(AAS),
∴AO=BG=3,AH=EO=6,CH=DF=4,BH=CF=3,
∵梯形DEOF的面积= (EF+DH) FH=80,
S△AEO=S△ABH= AF AE=9,
S△BCH=S△CDF= CH DH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故答案为:B.
【分析】根据题意,可利用AAS证△AEO≌△BAH,△BCH≌△CDF,可求得AO=BH,AH=EO,CH=DF,BH=CF,即可求得梯形DEOF的面积和△AEO,△ABH,△CGH,△CDF的面积,结合图形可求解.
6.【答案】SAS
【解析】【解答】解:∵∠1=∠2,
∴∠ADC=∠ADB,
∵CD=BD,AD=AD,
满足全等三角形判定定理SAS;
故答案为:SAS.
【分析】根据全等三角形的判定方法进行分析即可.
7.【答案】解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△FCE中
∴△ADE≌△CFE(AAS),
∴AD=CF=4,
∵AB=6,
∴DB=AB﹣AD=6﹣4=2
【解析】【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=6,FC=4,即可求线段DB的长.
8.【答案】解:添加的条件是AF=DE,理由如下:
∵AB=CD,
∴AB+BC=CD+BC,即AC=DB,
在△AFC和△DEB中,
∴
【解析】【分析】 添加的条件是AF=DE,先根据线段之和证出AC=DB, 再根据SAS定理即可证出 AFC≌ DEB.
9.【答案】(1)证明:∵△ABD和△ACE为等边三角形, ∴∠EAC=∠DAB=60°,
∴∠DAB+∠BAC=∠EAC+∠CAB,
∴∠DAC=∠EAB, ∵AD=AB,AC=AE, ∴△ADC≌△ABE(SAS), ∴BE=DC;
(2)解:过A点作△ABC的高线,垂足为F. ∵∠BAD=∠EAC,
∴∠BAD﹣∠EAD=∠EAC﹣∠EAD,
∴∠BAE=∠DAC, ∵AB=AD,AE=AC ∴△ABE≌△ADC(SAS), ∴DC=BE=2, ∵EC=3, ∴BC=5,
∵△ABC的面积是25cm2,
∴ , ∴AF=10,
∴△ABE的面积是 =10cm2
∴△ABE的面积是10cm2.
【解析】【分析】探究:证明△ADC≌△ABE(SAS),可得BE=DC;应用:过A点作△ABC的高线,垂足为F.先证明△ADC≌△ABE,可得BE=DC=2,利用面积求得AF=10,则△ABE的面积可求出.
10.【答案】(1);
(2)证明:结论仍然成立,理由如下:如图,
∵,
∴,
∴,
又∵,,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
【解析】【解答】(1)延长BD交CE于F,如下图:
在和中
∴
∴
∵,
∴
∵
∴
∴
故答案为: , .
【分析】(1)由“SAS”可证△ABD≌△ACE,可BD=CE,∠ABD=∠ACE,由直角三角形两锐角互余及三角形的内角和定理可得∠BHE=90°,从而根据垂直的定义证得BD⊥CE;
(2)由“SAS”可证△ABD≌△ACE,可得BD=CE,∠1=∠2,由直角三角形两锐角互余及三角形的内角和定理可得∠HDC=90°,从而根据垂直的定义证得BD⊥CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
12.2 三角形全等的判定一课一练
一、单选题
1.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是: ( )
A.带①去 B.带②去 C.带③去 D.带①和②
2.下列判断正确的是( )
A.有一条直角边对应相等的两个直角三角形全等
B.腰相等的两个等腰三角形全等
C.斜边相等的两个等腰直角三角形全等
D.有一个锐角对应相等的两个直角三角形全等
3.下列方法中,不能判定三角形全等的是 ( )
A.AAA B.SSS C.ASA D.SAS
4.如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形( )
A.8对 B.4对 C.2对 D.1对
5.如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )
A.30 B.50 C.66 D.80
二、填空题
6.如图,∠1=∠2,CD=BD,可证△ABD≌△ACD,则依据是 。
三、计算题
7.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.
四、解答题
8.如图,已知A、B、B、D,四点在同一直线上,AB=CD,∠A=∠B,请你填一个直接条件,_▲_,使 ,并说明理由.
五、综合题
9.
(1)感知:如图(1),在△ABC中,分别以AB、AC为边在△ABC外部作等边三角形△ABD、△ACE,连接CD、BE.求证:BE=DC;
(2)应用:如图(2),在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰三角形△ABD、△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为25cm2,求△ABE的面积.
六、实践探究题
10.有公共顶点的等腰直角三角形与等腰直角三角形按如图①所示放置,,,,点在上,点在的延长线上.连接,.
(1)【观察猜想】
与之间的数量关系是 ;位置关系是 .
(2)【探究证明】
将等腰直角三角形绕点逆时针旋转,如图②所示,使点,,在同一条直线上,连接,交于点.与之间的关系是否仍然成立?请说明理由
答案解析部分
1.【答案】C
【解析】【解答】解:
第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;第二块,仅保留了原三角形的一部分边,所以该块不行;第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定定理,所以应该拿这块去.
故答案为:C.
【分析】有全等三角形的判定可知角边角可以确定,即③可以。
2.【答案】C
【解析】【解答】解:有一条直角边对应相等的两个直角三角形,只知道一边和一角相等,不能判定全等,A不符合题意;
腰相等的两个等腰三角形,只知道两边相等,不能判定全等,B不符合题意;
斜边相等的两个等腰直角三角形,知道三个角和一个边全等,可以通过角角边或角边角判定全等,C符合题意;
D、有一个锐角对应相等的两个直角三角形,只知道三个角相等,不能判定全等,D不符合题意;
故答案为:C
【分析】根据全等三角形的判定方法逐项判断即可。
3.【答案】A
【解析】【解答】解:因为全等三角形的判定定理有“ ”,“ ”,“ ”,“ ”.
三个角相等不等判定三角形全等,只能判定相似.
故答案为:A.
【分析】全等三角形的判定定理有“ ”,“ ”,“ ”,“ ”等判定定理.不符合条件的即我们要找的答案.
4.【答案】B
【解析】【解答】解:∵AB∥CD,AD∥BC,
∴∠CAD=∠ACB,∠BDA=∠DBC,∠BAC=∠DCA,∠ABD=∠CDB,
又∵AC、BD为公共边,
∴△ACD≌△CAB、△BAD≌△DCB(ASA);
∴AD=BC,AB=CD,
∴△AOD≌△COB、△AOB≌△COD(ASA).
所以全等三角形有:△AOD≌△COB、△AOB≌△COD、△ACD≌△CAB、△BAD≌△DCB,共4对;故选B.
【分析】根据AB∥CD,AD∥BC可得到相等的角,再根据公共边AC、BD易证得:△ACD≌△CAB、△BAD≌△DCB(ASA);由上可得AD=BC、AB=CD,再根据平行线确定的角相等可证得:△AOD≌△COB、△AOB≌△COD(ASA).
5.【答案】B
【解析】【解答】∵∠EAO+∠BAH=90°,∠EAO+∠AEO=90°,
∴∠BAH=∠AEO,
∵在△AEO和△BAH中,
,
∴△AEO≌△BAH(AAS),
同理△BCH≌△CDF(AAS),
∴AO=BG=3,AH=EO=6,CH=DF=4,BH=CF=3,
∵梯形DEOF的面积= (EF+DH) FH=80,
S△AEO=S△ABH= AF AE=9,
S△BCH=S△CDF= CH DH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故答案为:B.
【分析】根据题意,可利用AAS证△AEO≌△BAH,△BCH≌△CDF,可求得AO=BH,AH=EO,CH=DF,BH=CF,即可求得梯形DEOF的面积和△AEO,△ABH,△CGH,△CDF的面积,结合图形可求解.
6.【答案】SAS
【解析】【解答】解:∵∠1=∠2,
∴∠ADC=∠ADB,
∵CD=BD,AD=AD,
满足全等三角形判定定理SAS;
故答案为:SAS.
【分析】根据全等三角形的判定方法进行分析即可.
7.【答案】解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△FCE中
∴△ADE≌△CFE(AAS),
∴AD=CF=4,
∵AB=6,
∴DB=AB﹣AD=6﹣4=2
【解析】【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=6,FC=4,即可求线段DB的长.
8.【答案】解:添加的条件是AF=DE,理由如下:
∵AB=CD,
∴AB+BC=CD+BC,即AC=DB,
在△AFC和△DEB中,
∴
【解析】【分析】 添加的条件是AF=DE,先根据线段之和证出AC=DB, 再根据SAS定理即可证出 AFC≌ DEB.
9.【答案】(1)证明:∵△ABD和△ACE为等边三角形, ∴∠EAC=∠DAB=60°,
∴∠DAB+∠BAC=∠EAC+∠CAB,
∴∠DAC=∠EAB, ∵AD=AB,AC=AE, ∴△ADC≌△ABE(SAS), ∴BE=DC;
(2)解:过A点作△ABC的高线,垂足为F. ∵∠BAD=∠EAC,
∴∠BAD﹣∠EAD=∠EAC﹣∠EAD,
∴∠BAE=∠DAC, ∵AB=AD,AE=AC ∴△ABE≌△ADC(SAS), ∴DC=BE=2, ∵EC=3, ∴BC=5,
∵△ABC的面积是25cm2,
∴ , ∴AF=10,
∴△ABE的面积是 =10cm2
∴△ABE的面积是10cm2.
【解析】【分析】探究:证明△ADC≌△ABE(SAS),可得BE=DC;应用:过A点作△ABC的高线,垂足为F.先证明△ADC≌△ABE,可得BE=DC=2,利用面积求得AF=10,则△ABE的面积可求出.
10.【答案】(1);
(2)证明:结论仍然成立,理由如下:如图,
∵,
∴,
∴,
又∵,,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
【解析】【解答】(1)延长BD交CE于F,如下图:
在和中
∴
∴
∵,
∴
∵
∴
∴
故答案为: , .
【分析】(1)由“SAS”可证△ABD≌△ACE,可BD=CE,∠ABD=∠ACE,由直角三角形两锐角互余及三角形的内角和定理可得∠BHE=90°,从而根据垂直的定义证得BD⊥CE;
(2)由“SAS”可证△ABD≌△ACE,可得BD=CE,∠1=∠2,由直角三角形两锐角互余及三角形的内角和定理可得∠HDC=90°,从而根据垂直的定义证得BD⊥CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
