13.1.2 线段的垂直平分线的性质一课一练(含解析)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质一课一练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 350.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 21:56:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.1.2 线段的垂直平分线的性质一课一练
一、填空题
1.在中,,边上的垂直平分线与所在的直线相交所得的锐角为40°,则的度数是 .
二、单选题
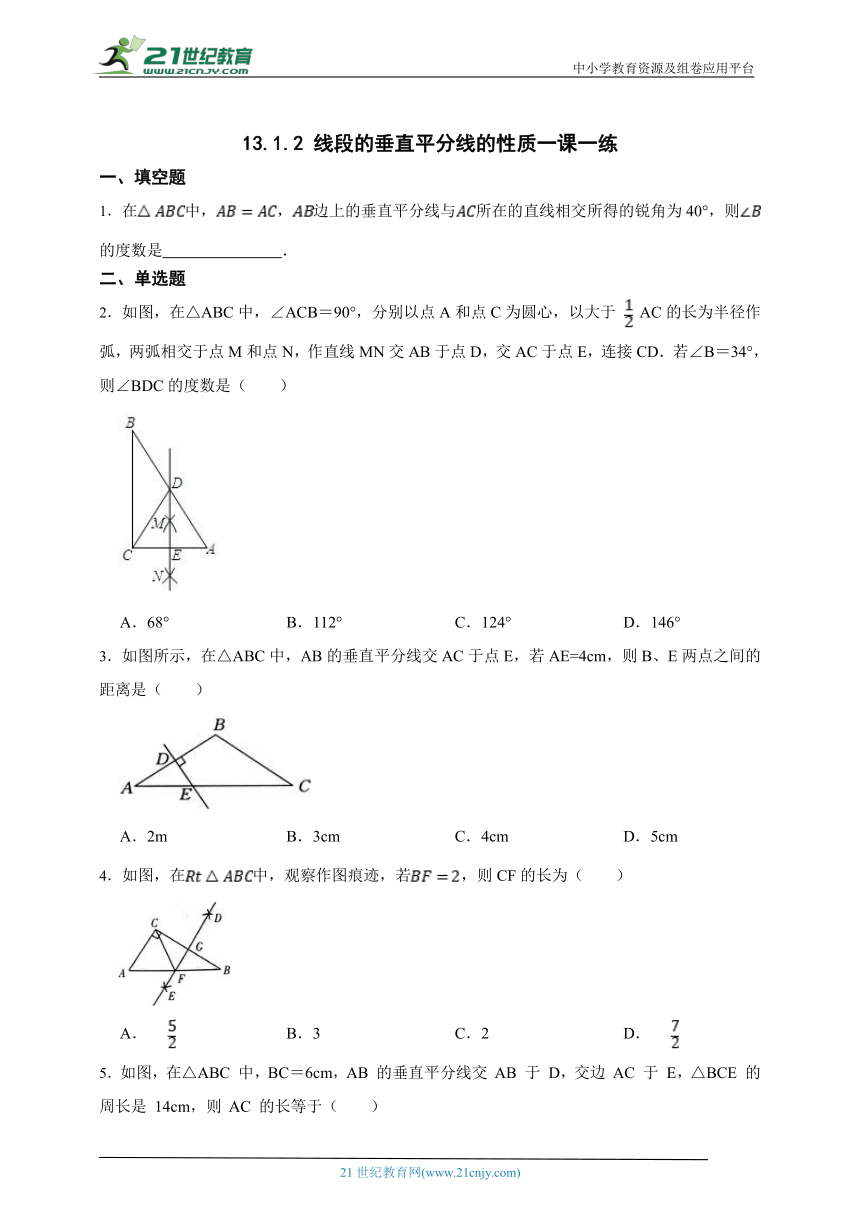
2.如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以大于 AC的长为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.若∠B=34°,则∠BDC的度数是( )
A.68° B.112° C.124° D.146°
3.如图所示,在△ABC中,AB的垂直平分线交AC于点E,若AE=4cm,则B、E两点之间的距离是( )
A.2m B.3cm C.4cm D.5cm
4.如图,在中,观察作图痕迹,若,则CF的长为( )
A. B.3 C.2 D.
5.如图,在△ABC 中,BC=6cm,AB 的垂直平分线交 AB 于 D,交边 AC 于 E,△BCE 的周长是 14cm,则 AC 的长等于( )
A.6cm B.8cm C.10cm D.12cm
6.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( ).
A.8 B.9 C.10 D.11
三、解答题
7.如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由:
解:∵CD是线段AB的垂直平分线,
∴AC= , =BD.
在△ACD和△BCD中,
∴ ≌ ( ).
∴∠CAD=∠CBD.
四、计算题
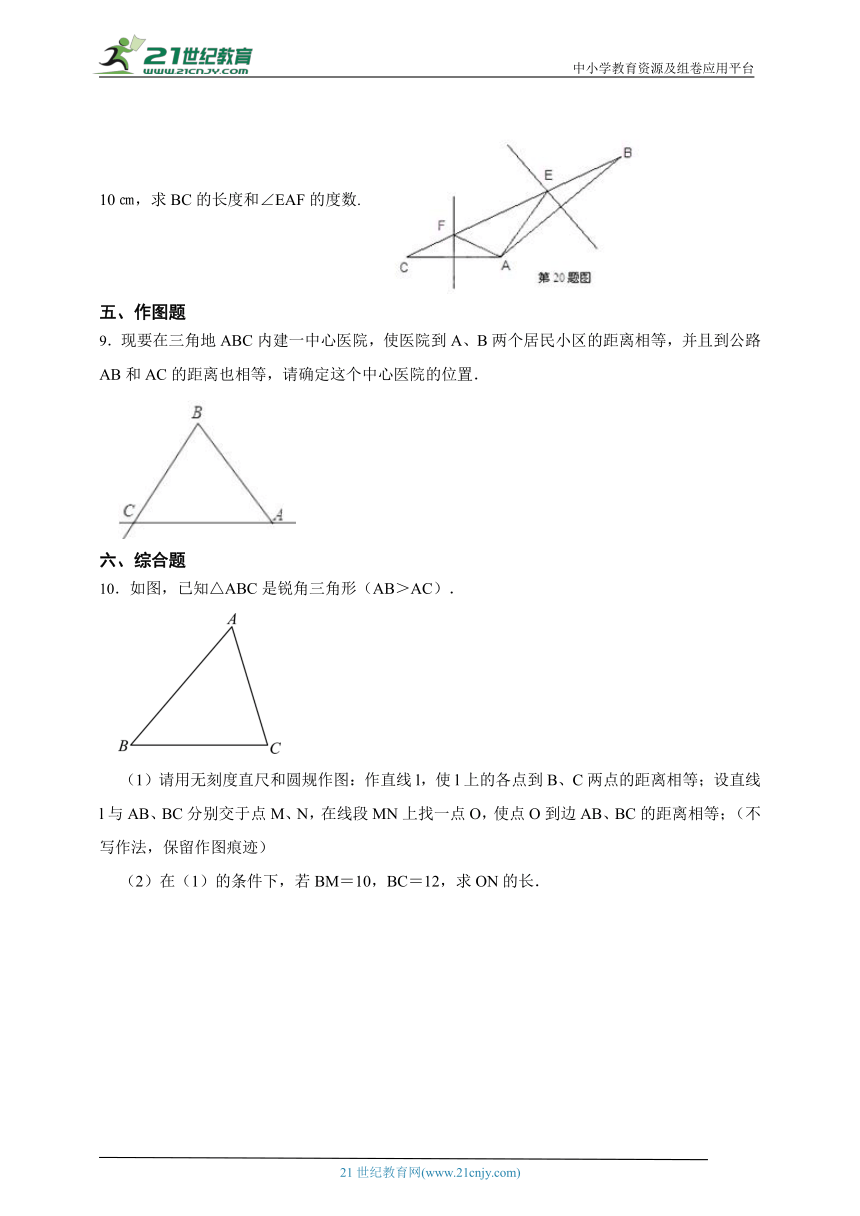
8.已知ABC中∠BAC=140°, AB、AC的垂直平分线分别交BC于E、F,AEF的周长为10㎝,求BC的长度和∠EAF的度数.
五、作图题
9.现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.
六、综合题
10.如图,已知△ABC是锐角三角形(AB>AC).
(1)请用无刻度直尺和圆规作图:作直线l,使l上的各点到B、C两点的距离相等;设直线l与AB、BC分别交于点M、N,在线段MN上找一点O,使点O到边AB、BC的距离相等;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若BM=10,BC=12,求ON的长.
答案解析部分
1.【答案】65°或25°
【解析】【解答】解:①如图:当△ABC中∠A为锐角时,则AB的中垂线MN与AC相交时,
∵∠AMD=90°,
∴∠A=90°-40°=50°,
∵AB=AC,
∴∠B=∠C=
=65°;
②如图:当△ABC中∠BAC为钝角时,则AB的中垂线MN与CA的延长线相交时,
∴∠DAB=90°-40°=50°,
∵AB=AC,
∴∠B=∠C=
∠DAB=25°.
故答案为:65°或25°.
【分析】①如图:当△ABC中∠A为锐角时,则AB的中垂线MN与AC相交时,②如图:当△ABC中∠BAC为钝角时,则AB的中垂线MN与CA的延长线相交时,分类讨论即可。
2.【答案】B
【解析】【解答】∵∠ACB=90°,∠B=34°,
∴∠A=56°,
∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=56°,
∴∠BCD=90°﹣56°=34°,
∴∠BDC=180°﹣34°﹣34°=112°,
故答案为:B.
【分析】根据题意可知DE是AC的垂直平分线,可得DA=DC,根据已知条件和等边对等角可求得∠DCA的度数,即可进一步求得∠BDC的度数.
3.【答案】C
【解析】【解答】解:如图所示:连接BE,
∵DE是线段AB的垂直平分线,
∴BE=AE,
∵AE=4,
∴BE=4.
故答案为:C
【分析】连接BE,根据线段垂直平分线上的点到线段两端的距离相等即可。
4.【答案】C
【解析】【解答】解:由作图痕迹可知,DE是BC的垂直平分线,
∴CF=BF=2,
故答案为:C.
【分析】根据垂直平分线的性质可得CF=BF=2。
5.【答案】B
【解析】【解答】解:∵DE是AB的垂直平分线,
∴AE=DE,
∵△BCE的周长等于14cm,
∴BC+CE+BE=BC+CE+AE=BC+AC=14cm,
∵BC=6cm,
∴AC=8cm.
故答案为:B.
【分析】根据线段垂直平分线上的点到线段两个端点的距离相等得出AE=DE,根据三角形周长的计算方法及等量代换和线段的和差得出BC+AC=14cm,从而即可得出答案.
6.【答案】B
【解析】【解答】解:∵DE是AB的垂直平分线
∴AE=BE
∵△BCE的周长为16 ,BC=7,
∴BC+BE+EC=16,∴BE+EC=9
∴AE+EC=9
即AC=9
∵AB=AC
∴AB=9
故答案为:B
【分析】根据垂直平分线定理可知AE=BE,利用△BCE的周长为16,BC=7,求得BE+EC=9,再等量代换即可求得AC=9,即AB=9.
7.【答案】解:∵CD是线段AB的垂直平分线,
∴AC=BC,AD=BD,
在△ACD和△BCD中, ,
∴△ACD≌△BCD(SSS),
∴∠CAD=∠CBD.
故答案为:BC,AD,AC,BD,公共边,△ACD,△BCD,SSS.
【解析】【分析】根据线段垂直平分线性质得出AC=BC,AD=BD,根据SSS证出△ACD≌△BCD即可.
8.【答案】解:∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF;
∵△AEF周长为:AE+EF+AF=BE+EF+CF=BC=10㎝,
∴BC=10㎝,
又∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∴∠B=∠BAE,∠C=∠CAF,
∵△ABC中,∠BAC=140°,
∴∠B+∠C=180°-∠BAC=40°,
∴∠BAE+∠CAF=40°,
∴∠EAF=∠BAC-(∠BAE+∠CAF)=140°-40°=100°。
【解析】【解答】由AB、AC的垂直平分线分别交BC于E、F,易证得AE=BE,AF=CF,然后由等腰三角形的性质,可得∠B=∠BAE,∠C=∠CAF,由△ABC中,∠BAC=140°,可求得∠B+∠C的度数,继而求得∠BAE+∠CAF的度数,继而求得∠EAF的度数;由△AEF周长为:AE+EF+AF=BE+EF+CF=BC,即可求得BC的长度。
【分析】此题主要考查了三角形内角和定理,等腰三角形性质和垂直平分线性质。
9.【答案】解:
作AB的垂直平分线EF,作∠BAC的角平分线AM,两线交于P,
则P为这个中心医院的位置.
【解析】【分析】根据线段的垂直评分线上的点到线段两端点的距离相等,角平分线上的点到角两边的距离相等,可作AB的垂直平分线,作∠BAC的角平分线,两线的交点即为所求。
10.【答案】(1)解:如图,直线MN,点O即为所求;
(2)解:过点O作OH⊥AB于点H.
∵BO平分∠ABC,ON⊥BC,OH⊥AB,
∴ON=OH,
∵MN垂直平分线段BC,
∴BN=CN=6,
∵BM=10,
∴MN===8,
∵S△BMN=S△BMO+S△BON,
∴×6×8=×10×OH+×6×ON,
∴ON=OH=3.
【解析】【分析】(1) 根据要求作出线段BC的垂直平分线和∠ABC的角平分线即可;
(2)先利用勾股定理求出MN的长,再结合S△BMN=S△BMO+S△BON,可得×6×8=×10×OH+×6×ON,最后求出ON=OH=3即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
13.1.2 线段的垂直平分线的性质一课一练
一、填空题
1.在中,,边上的垂直平分线与所在的直线相交所得的锐角为40°,则的度数是 .
二、单选题
2.如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以大于 AC的长为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.若∠B=34°,则∠BDC的度数是( )
A.68° B.112° C.124° D.146°
3.如图所示,在△ABC中,AB的垂直平分线交AC于点E,若AE=4cm,则B、E两点之间的距离是( )
A.2m B.3cm C.4cm D.5cm
4.如图,在中,观察作图痕迹,若,则CF的长为( )
A. B.3 C.2 D.
5.如图,在△ABC 中,BC=6cm,AB 的垂直平分线交 AB 于 D,交边 AC 于 E,△BCE 的周长是 14cm,则 AC 的长等于( )
A.6cm B.8cm C.10cm D.12cm
6.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( ).
A.8 B.9 C.10 D.11
三、解答题
7.如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由:
解:∵CD是线段AB的垂直平分线,
∴AC= , =BD.
在△ACD和△BCD中,
∴ ≌ ( ).
∴∠CAD=∠CBD.
四、计算题
8.已知ABC中∠BAC=140°, AB、AC的垂直平分线分别交BC于E、F,AEF的周长为10㎝,求BC的长度和∠EAF的度数.
五、作图题
9.现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.
六、综合题
10.如图,已知△ABC是锐角三角形(AB>AC).
(1)请用无刻度直尺和圆规作图:作直线l,使l上的各点到B、C两点的距离相等;设直线l与AB、BC分别交于点M、N,在线段MN上找一点O,使点O到边AB、BC的距离相等;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若BM=10,BC=12,求ON的长.
答案解析部分
1.【答案】65°或25°
【解析】【解答】解:①如图:当△ABC中∠A为锐角时,则AB的中垂线MN与AC相交时,
∵∠AMD=90°,
∴∠A=90°-40°=50°,
∵AB=AC,
∴∠B=∠C=
=65°;
②如图:当△ABC中∠BAC为钝角时,则AB的中垂线MN与CA的延长线相交时,
∴∠DAB=90°-40°=50°,
∵AB=AC,
∴∠B=∠C=
∠DAB=25°.
故答案为:65°或25°.
【分析】①如图:当△ABC中∠A为锐角时,则AB的中垂线MN与AC相交时,②如图:当△ABC中∠BAC为钝角时,则AB的中垂线MN与CA的延长线相交时,分类讨论即可。
2.【答案】B
【解析】【解答】∵∠ACB=90°,∠B=34°,
∴∠A=56°,
∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=56°,
∴∠BCD=90°﹣56°=34°,
∴∠BDC=180°﹣34°﹣34°=112°,
故答案为:B.
【分析】根据题意可知DE是AC的垂直平分线,可得DA=DC,根据已知条件和等边对等角可求得∠DCA的度数,即可进一步求得∠BDC的度数.
3.【答案】C
【解析】【解答】解:如图所示:连接BE,
∵DE是线段AB的垂直平分线,
∴BE=AE,
∵AE=4,
∴BE=4.
故答案为:C
【分析】连接BE,根据线段垂直平分线上的点到线段两端的距离相等即可。
4.【答案】C
【解析】【解答】解:由作图痕迹可知,DE是BC的垂直平分线,
∴CF=BF=2,
故答案为:C.
【分析】根据垂直平分线的性质可得CF=BF=2。
5.【答案】B
【解析】【解答】解:∵DE是AB的垂直平分线,
∴AE=DE,
∵△BCE的周长等于14cm,
∴BC+CE+BE=BC+CE+AE=BC+AC=14cm,
∵BC=6cm,
∴AC=8cm.
故答案为:B.
【分析】根据线段垂直平分线上的点到线段两个端点的距离相等得出AE=DE,根据三角形周长的计算方法及等量代换和线段的和差得出BC+AC=14cm,从而即可得出答案.
6.【答案】B
【解析】【解答】解:∵DE是AB的垂直平分线
∴AE=BE
∵△BCE的周长为16 ,BC=7,
∴BC+BE+EC=16,∴BE+EC=9
∴AE+EC=9
即AC=9
∵AB=AC
∴AB=9
故答案为:B
【分析】根据垂直平分线定理可知AE=BE,利用△BCE的周长为16,BC=7,求得BE+EC=9,再等量代换即可求得AC=9,即AB=9.
7.【答案】解:∵CD是线段AB的垂直平分线,
∴AC=BC,AD=BD,
在△ACD和△BCD中, ,
∴△ACD≌△BCD(SSS),
∴∠CAD=∠CBD.
故答案为:BC,AD,AC,BD,公共边,△ACD,△BCD,SSS.
【解析】【分析】根据线段垂直平分线性质得出AC=BC,AD=BD,根据SSS证出△ACD≌△BCD即可.
8.【答案】解:∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF;
∵△AEF周长为:AE+EF+AF=BE+EF+CF=BC=10㎝,
∴BC=10㎝,
又∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∴∠B=∠BAE,∠C=∠CAF,
∵△ABC中,∠BAC=140°,
∴∠B+∠C=180°-∠BAC=40°,
∴∠BAE+∠CAF=40°,
∴∠EAF=∠BAC-(∠BAE+∠CAF)=140°-40°=100°。
【解析】【解答】由AB、AC的垂直平分线分别交BC于E、F,易证得AE=BE,AF=CF,然后由等腰三角形的性质,可得∠B=∠BAE,∠C=∠CAF,由△ABC中,∠BAC=140°,可求得∠B+∠C的度数,继而求得∠BAE+∠CAF的度数,继而求得∠EAF的度数;由△AEF周长为:AE+EF+AF=BE+EF+CF=BC,即可求得BC的长度。
【分析】此题主要考查了三角形内角和定理,等腰三角形性质和垂直平分线性质。
9.【答案】解:
作AB的垂直平分线EF,作∠BAC的角平分线AM,两线交于P,
则P为这个中心医院的位置.
【解析】【分析】根据线段的垂直评分线上的点到线段两端点的距离相等,角平分线上的点到角两边的距离相等,可作AB的垂直平分线,作∠BAC的角平分线,两线的交点即为所求。
10.【答案】(1)解:如图,直线MN,点O即为所求;
(2)解:过点O作OH⊥AB于点H.
∵BO平分∠ABC,ON⊥BC,OH⊥AB,
∴ON=OH,
∵MN垂直平分线段BC,
∴BN=CN=6,
∵BM=10,
∴MN===8,
∵S△BMN=S△BMO+S△BON,
∴×6×8=×10×OH+×6×ON,
∴ON=OH=3.
【解析】【分析】(1) 根据要求作出线段BC的垂直平分线和∠ABC的角平分线即可;
(2)先利用勾股定理求出MN的长,再结合S△BMN=S△BMO+S△BON,可得×6×8=×10×OH+×6×ON,最后求出ON=OH=3即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
