13.1 轴对称本节综合题(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
13.1 轴对称本节综合题
一、填空题
1.如图,在△ABC中,∠B=65°,∠C=28°,分别以点A和点C为圆心,大于 画弧,两弧相交于点M,N,作直线MN,连接AD,则∠BAD的度数为 .
二、单选题
2.下列四个数学符号中,是轴对称图形的是( )
A. B. C. D.
3.下列大学的校徽图案是轴对称图形的是( )
A. B.
C. D.
4.以下是小明收集的四个轴对称图案,他收集错的是( )
A. B. C. D.
5.下列图形中,不是轴对称图形的是( )
A.等腰三角形 B.正方形 C.圆 D.平行四边形
6.如下书写的八个黑体字,其中为轴对称图形的有( )
A.0个 B.1个 C.2个 D.3个
7.下图是几种汽车的标志,其中属于轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
8.下列几何图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
9.下列图形中,是轴对称图形的是( )
A. B.
C. D.
10.冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )
A. B.
C. D.
11.下面的四个图案分别是“ 型路口”、“步行”、“注意落石”和“向左转弯”的交通标识,其中可以看作是轴对称图形的是( )
A. B.
C. D.
12.下列图标是节水、节能、低碳和绿色食品的标志,其中是轴对称图形的是( )
A. B. C. D.
13.“致中和,天地位焉,万物育焉”,对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光,在下列标识或简图中,是轴对称图形的是( )
A. B.
C. D.
14.如图,在△ABC中,分别以点A和点B为圆心,大于AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
A.3 B.3.5 C.5 D.7
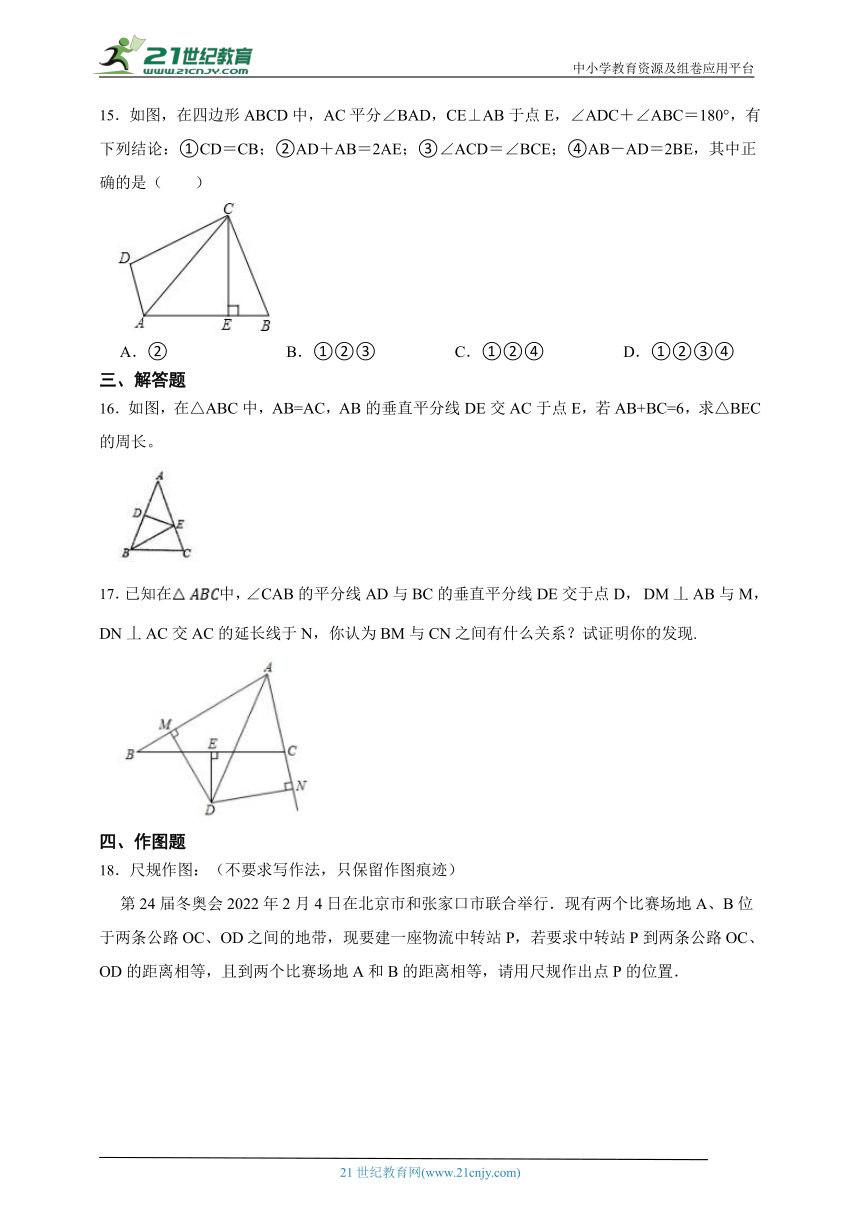
15.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE,其中正确的是( )
A.② B.①②③ C.①②④ D.①②③④
三、解答题
16.如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,若AB+BC=6,求△BEC的周长。
17.已知在中,∠CAB的平分线AD与BC的垂直平分线DE交于点D, DM丄AB与M, DN丄AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
四、作图题
18.尺规作图:(不要求写作法,只保留作图痕迹)
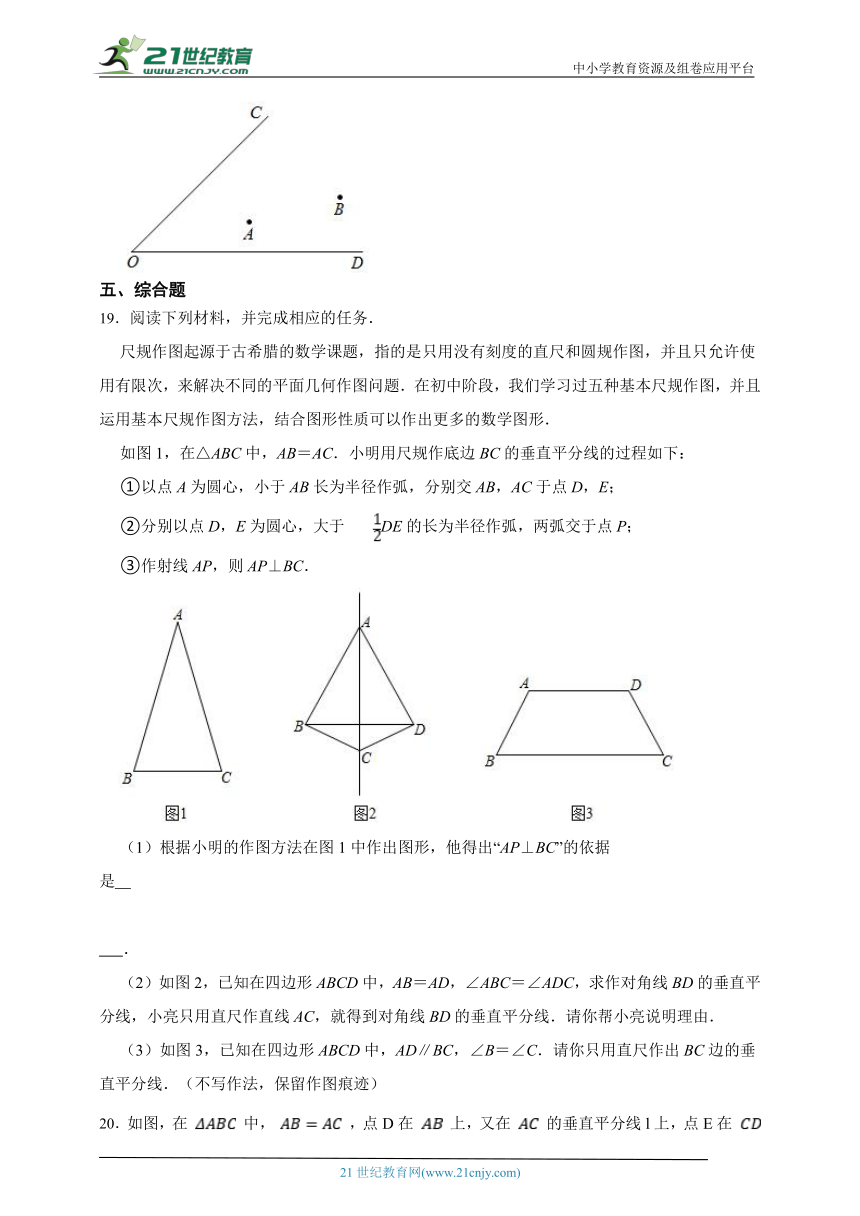
第24届冬奥会2022年2月4日在北京市和张家口市联合举行.现有两个比赛场地A、B位于两条公路OC、OD之间的地带,现要建一座物流中转站P,若要求中转站P到两条公路OC、OD的距离相等,且到两个比赛场地A和B的距离相等,请用尺规作出点P的位置.
五、综合题
19.阅读下列材料,并完成相应的任务.
尺规作图起源于古希腊的数学课题,指的是只用没有刻度的直尺和圆规作图,并且只允许使用有限次,来解决不同的平面几何作图问题.在初中阶段,我们学习过五种基本尺规作图,并且运用基本尺规作图方法,结合图形性质可以作出更多的数学图形.
如图1,在△ABC中,AB=AC.小明用尺规作底边BC的垂直平分线的过程如下:
①以点A为圆心,小于AB长为半径作弧,分别交AB,AC于点D,E;
②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于点P;
③作射线AP,则AP⊥BC.
(1)根据小明的作图方法在图1中作出图形,他得出“AP⊥BC”的依据是 .
(2)如图2,已知在四边形ABCD中,AB=AD,∠ABC=∠ADC,求作对角线BD的垂直平分线,小亮只用直尺作直线AC,就得到对角线BD的垂直平分线.请你帮小亮说明理由.
(3)如图3,已知在四边形ABCD中,AD∥BC,∠B=∠C.请你只用直尺作出BC边的垂直平分线.(不写作法,保留作图痕迹)
20.如图,在 中, ,点D在 上,又在 的垂直平分线l上,点E在 的延长线上,点F在 上, .
(1)试说明: .
(2)若 平分 ,求 的度数.
六、实践探究题
21.(问题提出)
如图①,在 中,若 , ,求 边上的中线 的取值范围.
(1)【问题解决】
解决此问题可以用如下方法:延长 到点 使 ,再连接 (或将 绕着点 逆时针旋转 得到 ),把 、 、 集中在 中,利用三角形三边的关系即可判断,由此得出中线 的取值范围.
(2)【应用】
如图②,在 中, 为 的中点,已知 , , ,求 的长.
(3)【拓展】
如图③,在 中, ,点 是边 的中点,点 在边 上,过点 作 交边 于点 ,连接 。已知 , ,求 的长.
答案解析部分
1.【答案】59°
【解析】【解答】解:∵△ABC中,∠B=55°,∠C=28°,
∴∠BAC=180°-65°-28°=87°.
∵直线MN是线段AC的垂直平分线,
∴∠C=∠CAD=28°,
∴∠BAD=∠BAC-∠CAD=87°-28°=59°.
故答案为:59°.
【分析】先根据三角形内角和定理求出角BAC的度数,再由线段垂直平分线的性质得出∠C=∠CAD,进而可得出答案。
2.【答案】A
【解析】【解答】解:A选项,符合轴对称图形的定义,正确;
B选项,不符合轴对称图形的定义,错误;
C选项,不符合轴对称图形的定义,错误;
D选项,不符合轴对称图形的定义,错误.
故答案为:A.
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,从而即可判定.
3.【答案】B
【解析】【解答】解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故答案为:B.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
4.【答案】C
【解析】【解答】解:A、是轴对称图形,不符合题意;
B、是轴对称图形,不符合题意;
C、不是轴对称图形,符合题意;
D、是轴对称图形,不符合题意.
故答案为:C.
【分析】轴对称图形是如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
5.【答案】D
【解析】【解答】解:A.等腰三角形是轴对称图形,故此选项不合题意;
B.正方形是轴对称图形,故此选项不合题意;
C.圆是轴对称图形,故此选项不合题意;
D.平行四边形不是轴对称图形,故此选项符合题意;
故答案为:D.
【分析】根据轴对称图形的定义即可得出。
6.【答案】A
【解析】【解答】解:观察书写的8个汉字,没有轴对称图形.
故答案为:A.
【分析】轴对称图形沿一条轴折叠180°,被折叠两部分能完全重合,据此逐项分析判断即可。
7.【答案】C
【解析】【解答】解:观察图形可知,只有第三个图形不属于轴对称图形
因此,属于轴对称图形的有3个
故答案为:C.
【分析】根据轴对称图形的定义“平面内,一个图形沿一条直线折叠,如果直线两旁的部分能够完全重合,这个图形就是轴对称图形”逐个判断即可.
8.【答案】D
【解析】【解答】解:A、即不是轴对称图形也不是中心对称图形,不符合题意;
B、是轴对称图形但不是中心对称图形,不符合题意;
C、是中心对称图形但不是轴对称图形,不符合题意;
D、即是轴对称图形也是中心对称图形,符合题意;
故答案为:D.
【分析】考查轴对称图形与中心对称图形的概念。
9.【答案】B
【解析】【解答】解:A、不是轴对称图形,故此选项不合题意;
B、是轴对称图形,故此选项符合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意;
故答案为:B.
【分析】根据轴对称图形的概念求解.
10.【答案】D
【解析】【解答】解:观察图形可发现 是轴对称图形,
故答案为:D.
【分析】根据轴对称图形的特征直接判断即可.
11.【答案】A
【解析】【解答】A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项不符合题意;
故答案为:A.
【分析】根据轴对称图形的定义逐项判定即可。
12.【答案】D
【解析】【解答】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
【分析】根据轴对称图形的概念对各选项分析判断利用排除法求解
13.【答案】A
【解析】【解答】解:A、是轴对称图形说法正确,符合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、不是轴对称图形,故本选项不合题意.
故答案为:A.
【分析】 在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形 。根据轴对称图形的定义对每个选项一一判断求解即可。
14.【答案】B
【解析】【解答】解:根据题意可得MN是AB的垂直平分线,
∵△ADC的周长为9,
∴AC+AD+CD=9,
∵△ABC的周长等于16,
∴AC+CD+BD+AB=16,
∵MN是AB的垂直平分线,
∴AD=BD,AE=AB,
∴AC+CD+AD+AB=16,
∴AB=16﹣9=7,
∴AE=3.5.
故选:B.
【分析】根据作图过程可得MN是AB的垂直平分线,进而可得AD=BD,AE=AB,再由△ABC的周长等于16,△ADC的周长为9,可得AC+AD+CD=9,AC+CD+BD+AB=16,两式相减可得答案.
15.【答案】C
【解析】【解答】解:在EA上截取EF=BE,连接CF,
∵CE⊥AB,
∴CF=CB,
∴∠CFB=∠B,
∵∠AFC+∠CFB=180°,∠ADC+∠ABC=180°,
∴∠D=∠AFC,
∵AC平分∠BAD,
即∠DAC=∠FAC,
在△ACD和△ACF中,
,
∴△ACD≌△ACF(AAS),
∴CD=CF,
∴CD=CB,
故①正确;
∴AD=AF,
∴AD+AB=AF+AE+BE=AF+EF+AE=AE+AE=2AE.
故②正确;
根据已知条件无法证明∠ACD=∠BCE,
故③错误;
AB-AD=AB-AF=BF=2BE,
故④正确.
其中正确的是①②④.
故答案为:C.
【分析】在EA上截取EF=BE,连接CF,根据“AC平分∠BAD”和“∠ADC+∠ABC=180°”证明出△ACD≌△ACF,故①正确;由①可知,AD=AF,再根据线段间的和差关系可得:AD+AB=2AE,AB-AD=2BE,故②④正确.
16.【答案】解:∵ED是AB上的垂直平分线
∴AE=BE
∵AC+BC=6,∴△BCE的周长为EC+EB+BC=BC+(EC+EB)=BC+(EC+AE)=BC+AC=6
【解析】【分析】根据垂直平分线的性质可知: AE=BE ,结合 AB=AC,即可求出△BEC的周长.
17.【答案】解:,证明如下:
如图,连接BD,CD,
∵AD平分,,,
∴,
∵DE垂直平分BC,
∴,
在与中,,
∴,
∴.
【解析】【分析】连接BD,CD,根据角平分线的性质可得DM=DN,根据垂直平分线的性质可得BD=CD,然后利用HL证明△BMD≌△CND,据此可得结论.
18.【答案】解:如图所示点P为所求.
【解析】【分析】根据要求作出图象即可。
19.【答案】(1)作图如下: 得出“AP⊥BC”的依据是:等腰三角形顶角的平分线与底边上的高和底边上的中线互相重合; 故答案为:等腰三角形顶角的平分线与底边上的高和底边上的中线互相重合;
(2)解:∵AB=AD,
∴点A在线段BD的垂直平分线上,∠ABD=∠ADB
∵∠ABC=∠ADC,
∴∠CBD=∠CDB,
∴CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是对角线BD的垂直平分线;
(3)解:如图,直线n即为所求.
【解析】【分析】(1)根据题意作图,再求解即可;
(2)先求出点A在线段BD的垂直平分线上,∠ABD=∠ADB ,再求出 CB=CD ,最后求解即可;
(3)根据作垂直平分线的方法作图即可。
20.【答案】(1)解:∵点 在 的垂直平分线l上,
∴ ,
∴ ,
在 和 中,
, , ,
∴
(2)解:∵ ,
∴ ,
∵ 平分 , ,
∴ ,
∴ ,
∵ ,
∴ ,
由(1)知, ,
∴ ,
∵ ,
∴
【解析】【分析】(1)利用垂直平分线上的点到线段两端点的距离相等,可证得AD=CD;再利用等边对等角可证得∠DAC=∠DCA;然后利用SAS可证得结论。
(2)利用等边对等角可证得∠ABC=∠ACB,利用角平分线的定义去证明∠ACD=∠DAC=∠BCD;再求出△ABC的三个内角的度数,利用全等三角形的性质就可求出∠ABF=∠CAE=∠DAE+36°;然后利用∠ABC=72°,可求出∠ABF+∠FBC的值。
21.【答案】(1)解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AB-AC<AE<AC+AB,
∴2<AE<10,
∵AE=2AD,
∴,1<AD<5,
即:BC边上的中线AD的取值范围1<AD<5
(2)解:延长AD至E,使DE=AD,连接BE.
∵点D为边BC的中点,
∴BD=CD.
∵∠BDE=∠ADC,
∴△ADC≌△EDB.
∴BE=AC=3,DE=AD=2.
∴AE=4.
∵AB=5,且 ,
∴ .
∴△ABE为直角三角形,∠AEB=90°.
∵在Rt△BDE中,∠BED=90°,
∴BD= ,
∴BC=2BD=
(3)解:延长ED到点G,使DG=ED,连接CG,FG.
同前法可得△EBD≌△GCD,
∴∠B=∠GCD,BE=CG=4,
又∵∠A=90°,
∴∠B+∠BCA=90°,
∴∠GCD+∠BCA=90°,即∠GCF=90°,
∵CG=4,CF=5,
∴FG= = = .
∴EF= FG =
【解析】【分析】(1)延长AD到E,使AD=DE,连接BE,先利用SAS证△ADC≌△EDB,根据全等三角形对应边相等得出EB=AC,根据三角形的三边关系求出即可;
(2) :延长AD至E,使DE=AD,连接BE. 同(1)可证△ADC≌△EDB,根据全等三角形的对应边相等得出 BE=AC=3,DE=AD=2. 进而而出AE的长,利用勾股定理的逆定理判断出△ABE为直角三角形,然后在Rt△BED中利用勾股定理求出BD的长,进而得出BC的长;
(3)延长ED到点G,使DG=ED,连接CG,FG. 同前法可得△EBD≌△GCD, 根据全等三角形的性质得出∠B=∠GCD、BE=CG=4,根据直角三角形的两锐角互余得出 ∠B+∠BCA=90°, 故 ∠GCD+∠BCA=90°,即 ∠GCF=90°,利用勾股定理求得FG的长,最后由中垂线性质即可得EF=FG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
13.1 轴对称本节综合题
一、填空题
1.如图,在△ABC中,∠B=65°,∠C=28°,分别以点A和点C为圆心,大于 画弧,两弧相交于点M,N,作直线MN,连接AD,则∠BAD的度数为 .
二、单选题
2.下列四个数学符号中,是轴对称图形的是( )
A. B. C. D.
3.下列大学的校徽图案是轴对称图形的是( )
A. B.
C. D.
4.以下是小明收集的四个轴对称图案,他收集错的是( )
A. B. C. D.
5.下列图形中,不是轴对称图形的是( )
A.等腰三角形 B.正方形 C.圆 D.平行四边形
6.如下书写的八个黑体字,其中为轴对称图形的有( )
A.0个 B.1个 C.2个 D.3个
7.下图是几种汽车的标志,其中属于轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
8.下列几何图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
9.下列图形中,是轴对称图形的是( )
A. B.
C. D.
10.冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )
A. B.
C. D.
11.下面的四个图案分别是“ 型路口”、“步行”、“注意落石”和“向左转弯”的交通标识,其中可以看作是轴对称图形的是( )
A. B.
C. D.
12.下列图标是节水、节能、低碳和绿色食品的标志,其中是轴对称图形的是( )
A. B. C. D.
13.“致中和,天地位焉,万物育焉”,对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光,在下列标识或简图中,是轴对称图形的是( )
A. B.
C. D.
14.如图,在△ABC中,分别以点A和点B为圆心,大于AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
A.3 B.3.5 C.5 D.7
15.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE,其中正确的是( )
A.② B.①②③ C.①②④ D.①②③④
三、解答题
16.如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,若AB+BC=6,求△BEC的周长。
17.已知在中,∠CAB的平分线AD与BC的垂直平分线DE交于点D, DM丄AB与M, DN丄AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
四、作图题
18.尺规作图:(不要求写作法,只保留作图痕迹)
第24届冬奥会2022年2月4日在北京市和张家口市联合举行.现有两个比赛场地A、B位于两条公路OC、OD之间的地带,现要建一座物流中转站P,若要求中转站P到两条公路OC、OD的距离相等,且到两个比赛场地A和B的距离相等,请用尺规作出点P的位置.
五、综合题
19.阅读下列材料,并完成相应的任务.
尺规作图起源于古希腊的数学课题,指的是只用没有刻度的直尺和圆规作图,并且只允许使用有限次,来解决不同的平面几何作图问题.在初中阶段,我们学习过五种基本尺规作图,并且运用基本尺规作图方法,结合图形性质可以作出更多的数学图形.
如图1,在△ABC中,AB=AC.小明用尺规作底边BC的垂直平分线的过程如下:
①以点A为圆心,小于AB长为半径作弧,分别交AB,AC于点D,E;
②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于点P;
③作射线AP,则AP⊥BC.
(1)根据小明的作图方法在图1中作出图形,他得出“AP⊥BC”的依据是 .
(2)如图2,已知在四边形ABCD中,AB=AD,∠ABC=∠ADC,求作对角线BD的垂直平分线,小亮只用直尺作直线AC,就得到对角线BD的垂直平分线.请你帮小亮说明理由.
(3)如图3,已知在四边形ABCD中,AD∥BC,∠B=∠C.请你只用直尺作出BC边的垂直平分线.(不写作法,保留作图痕迹)
20.如图,在 中, ,点D在 上,又在 的垂直平分线l上,点E在 的延长线上,点F在 上, .
(1)试说明: .
(2)若 平分 ,求 的度数.
六、实践探究题
21.(问题提出)
如图①,在 中,若 , ,求 边上的中线 的取值范围.
(1)【问题解决】
解决此问题可以用如下方法:延长 到点 使 ,再连接 (或将 绕着点 逆时针旋转 得到 ),把 、 、 集中在 中,利用三角形三边的关系即可判断,由此得出中线 的取值范围.
(2)【应用】
如图②,在 中, 为 的中点,已知 , , ,求 的长.
(3)【拓展】
如图③,在 中, ,点 是边 的中点,点 在边 上,过点 作 交边 于点 ,连接 。已知 , ,求 的长.
答案解析部分
1.【答案】59°
【解析】【解答】解:∵△ABC中,∠B=55°,∠C=28°,
∴∠BAC=180°-65°-28°=87°.
∵直线MN是线段AC的垂直平分线,
∴∠C=∠CAD=28°,
∴∠BAD=∠BAC-∠CAD=87°-28°=59°.
故答案为:59°.
【分析】先根据三角形内角和定理求出角BAC的度数,再由线段垂直平分线的性质得出∠C=∠CAD,进而可得出答案。
2.【答案】A
【解析】【解答】解:A选项,符合轴对称图形的定义,正确;
B选项,不符合轴对称图形的定义,错误;
C选项,不符合轴对称图形的定义,错误;
D选项,不符合轴对称图形的定义,错误.
故答案为:A.
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,从而即可判定.
3.【答案】B
【解析】【解答】解:A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故答案为:B.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
4.【答案】C
【解析】【解答】解:A、是轴对称图形,不符合题意;
B、是轴对称图形,不符合题意;
C、不是轴对称图形,符合题意;
D、是轴对称图形,不符合题意.
故答案为:C.
【分析】轴对称图形是如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
5.【答案】D
【解析】【解答】解:A.等腰三角形是轴对称图形,故此选项不合题意;
B.正方形是轴对称图形,故此选项不合题意;
C.圆是轴对称图形,故此选项不合题意;
D.平行四边形不是轴对称图形,故此选项符合题意;
故答案为:D.
【分析】根据轴对称图形的定义即可得出。
6.【答案】A
【解析】【解答】解:观察书写的8个汉字,没有轴对称图形.
故答案为:A.
【分析】轴对称图形沿一条轴折叠180°,被折叠两部分能完全重合,据此逐项分析判断即可。
7.【答案】C
【解析】【解答】解:观察图形可知,只有第三个图形不属于轴对称图形
因此,属于轴对称图形的有3个
故答案为:C.
【分析】根据轴对称图形的定义“平面内,一个图形沿一条直线折叠,如果直线两旁的部分能够完全重合,这个图形就是轴对称图形”逐个判断即可.
8.【答案】D
【解析】【解答】解:A、即不是轴对称图形也不是中心对称图形,不符合题意;
B、是轴对称图形但不是中心对称图形,不符合题意;
C、是中心对称图形但不是轴对称图形,不符合题意;
D、即是轴对称图形也是中心对称图形,符合题意;
故答案为:D.
【分析】考查轴对称图形与中心对称图形的概念。
9.【答案】B
【解析】【解答】解:A、不是轴对称图形,故此选项不合题意;
B、是轴对称图形,故此选项符合题意;
C、不是轴对称图形,故此选项不合题意;
D、不是轴对称图形,故此选项不合题意;
故答案为:B.
【分析】根据轴对称图形的概念求解.
10.【答案】D
【解析】【解答】解:观察图形可发现 是轴对称图形,
故答案为:D.
【分析】根据轴对称图形的特征直接判断即可.
11.【答案】A
【解析】【解答】A、是轴对称图形,故此选项符合题意;
B、不是轴对称图形,故此选项不符合题意;
C、不是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项不符合题意;
故答案为:A.
【分析】根据轴对称图形的定义逐项判定即可。
12.【答案】D
【解析】【解答】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
【分析】根据轴对称图形的概念对各选项分析判断利用排除法求解
13.【答案】A
【解析】【解答】解:A、是轴对称图形说法正确,符合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、不是轴对称图形,故本选项不合题意.
故答案为:A.
【分析】 在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形 。根据轴对称图形的定义对每个选项一一判断求解即可。
14.【答案】B
【解析】【解答】解:根据题意可得MN是AB的垂直平分线,
∵△ADC的周长为9,
∴AC+AD+CD=9,
∵△ABC的周长等于16,
∴AC+CD+BD+AB=16,
∵MN是AB的垂直平分线,
∴AD=BD,AE=AB,
∴AC+CD+AD+AB=16,
∴AB=16﹣9=7,
∴AE=3.5.
故选:B.
【分析】根据作图过程可得MN是AB的垂直平分线,进而可得AD=BD,AE=AB,再由△ABC的周长等于16,△ADC的周长为9,可得AC+AD+CD=9,AC+CD+BD+AB=16,两式相减可得答案.
15.【答案】C
【解析】【解答】解:在EA上截取EF=BE,连接CF,
∵CE⊥AB,
∴CF=CB,
∴∠CFB=∠B,
∵∠AFC+∠CFB=180°,∠ADC+∠ABC=180°,
∴∠D=∠AFC,
∵AC平分∠BAD,
即∠DAC=∠FAC,
在△ACD和△ACF中,
,
∴△ACD≌△ACF(AAS),
∴CD=CF,
∴CD=CB,
故①正确;
∴AD=AF,
∴AD+AB=AF+AE+BE=AF+EF+AE=AE+AE=2AE.
故②正确;
根据已知条件无法证明∠ACD=∠BCE,
故③错误;
AB-AD=AB-AF=BF=2BE,
故④正确.
其中正确的是①②④.
故答案为:C.
【分析】在EA上截取EF=BE,连接CF,根据“AC平分∠BAD”和“∠ADC+∠ABC=180°”证明出△ACD≌△ACF,故①正确;由①可知,AD=AF,再根据线段间的和差关系可得:AD+AB=2AE,AB-AD=2BE,故②④正确.
16.【答案】解:∵ED是AB上的垂直平分线
∴AE=BE
∵AC+BC=6,∴△BCE的周长为EC+EB+BC=BC+(EC+EB)=BC+(EC+AE)=BC+AC=6
【解析】【分析】根据垂直平分线的性质可知: AE=BE ,结合 AB=AC,即可求出△BEC的周长.
17.【答案】解:,证明如下:
如图,连接BD,CD,
∵AD平分,,,
∴,
∵DE垂直平分BC,
∴,
在与中,,
∴,
∴.
【解析】【分析】连接BD,CD,根据角平分线的性质可得DM=DN,根据垂直平分线的性质可得BD=CD,然后利用HL证明△BMD≌△CND,据此可得结论.
18.【答案】解:如图所示点P为所求.
【解析】【分析】根据要求作出图象即可。
19.【答案】(1)作图如下: 得出“AP⊥BC”的依据是:等腰三角形顶角的平分线与底边上的高和底边上的中线互相重合; 故答案为:等腰三角形顶角的平分线与底边上的高和底边上的中线互相重合;
(2)解:∵AB=AD,
∴点A在线段BD的垂直平分线上,∠ABD=∠ADB
∵∠ABC=∠ADC,
∴∠CBD=∠CDB,
∴CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是对角线BD的垂直平分线;
(3)解:如图,直线n即为所求.
【解析】【分析】(1)根据题意作图,再求解即可;
(2)先求出点A在线段BD的垂直平分线上,∠ABD=∠ADB ,再求出 CB=CD ,最后求解即可;
(3)根据作垂直平分线的方法作图即可。
20.【答案】(1)解:∵点 在 的垂直平分线l上,
∴ ,
∴ ,
在 和 中,
, , ,
∴
(2)解:∵ ,
∴ ,
∵ 平分 , ,
∴ ,
∴ ,
∵ ,
∴ ,
由(1)知, ,
∴ ,
∵ ,
∴
【解析】【分析】(1)利用垂直平分线上的点到线段两端点的距离相等,可证得AD=CD;再利用等边对等角可证得∠DAC=∠DCA;然后利用SAS可证得结论。
(2)利用等边对等角可证得∠ABC=∠ACB,利用角平分线的定义去证明∠ACD=∠DAC=∠BCD;再求出△ABC的三个内角的度数,利用全等三角形的性质就可求出∠ABF=∠CAE=∠DAE+36°;然后利用∠ABC=72°,可求出∠ABF+∠FBC的值。
21.【答案】(1)解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AB-AC<AE<AC+AB,
∴2<AE<10,
∵AE=2AD,
∴,1<AD<5,
即:BC边上的中线AD的取值范围1<AD<5
(2)解:延长AD至E,使DE=AD,连接BE.
∵点D为边BC的中点,
∴BD=CD.
∵∠BDE=∠ADC,
∴△ADC≌△EDB.
∴BE=AC=3,DE=AD=2.
∴AE=4.
∵AB=5,且 ,
∴ .
∴△ABE为直角三角形,∠AEB=90°.
∵在Rt△BDE中,∠BED=90°,
∴BD= ,
∴BC=2BD=
(3)解:延长ED到点G,使DG=ED,连接CG,FG.
同前法可得△EBD≌△GCD,
∴∠B=∠GCD,BE=CG=4,
又∵∠A=90°,
∴∠B+∠BCA=90°,
∴∠GCD+∠BCA=90°,即∠GCF=90°,
∵CG=4,CF=5,
∴FG= = = .
∴EF= FG =
【解析】【分析】(1)延长AD到E,使AD=DE,连接BE,先利用SAS证△ADC≌△EDB,根据全等三角形对应边相等得出EB=AC,根据三角形的三边关系求出即可;
(2) :延长AD至E,使DE=AD,连接BE. 同(1)可证△ADC≌△EDB,根据全等三角形的对应边相等得出 BE=AC=3,DE=AD=2. 进而而出AE的长,利用勾股定理的逆定理判断出△ABE为直角三角形,然后在Rt△BED中利用勾股定理求出BD的长,进而得出BC的长;
(3)延长ED到点G,使DG=ED,连接CG,FG. 同前法可得△EBD≌△GCD, 根据全等三角形的性质得出∠B=∠GCD、BE=CG=4,根据直角三角形的两锐角互余得出 ∠B+∠BCA=90°, 故 ∠GCD+∠BCA=90°,即 ∠GCF=90°,利用勾股定理求得FG的长,最后由中垂线性质即可得EF=FG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
