13.2.2 用坐标表示轴对称一课一练(含解析)
文档属性
| 名称 | 13.2.2 用坐标表示轴对称一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 317.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
13.2.2 用坐标表示轴对称一课一练
一、填空题
1.若点A(3,-2)与点B关于Y轴对称,则点B的坐标为 .
二、单选题
2.点N(a,﹣b)关于x轴的对称点的坐标是( )
A.(a,b) B.(﹣a,﹣b)
C.(-a,b) D.(﹣b,a)
3.已知点A(a,-2)和B(3,b)关于x轴对称,应当满足条件( )
A.a=2,b=3 B.a=3,b=2 C.a=-3,b=2 D.a=2,b=-3
4.和点P(﹣3,2)关于x轴对称的点是( )
A.(3,2) B.(﹣3,2)
C.(3,﹣2) D.(﹣3,﹣2)
5.已知点关于x轴的对称点在第二象限,则a的取值范围是( )
A. B. C. D.
6.如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A.6 B.7 C.8 D.9
三、解答题
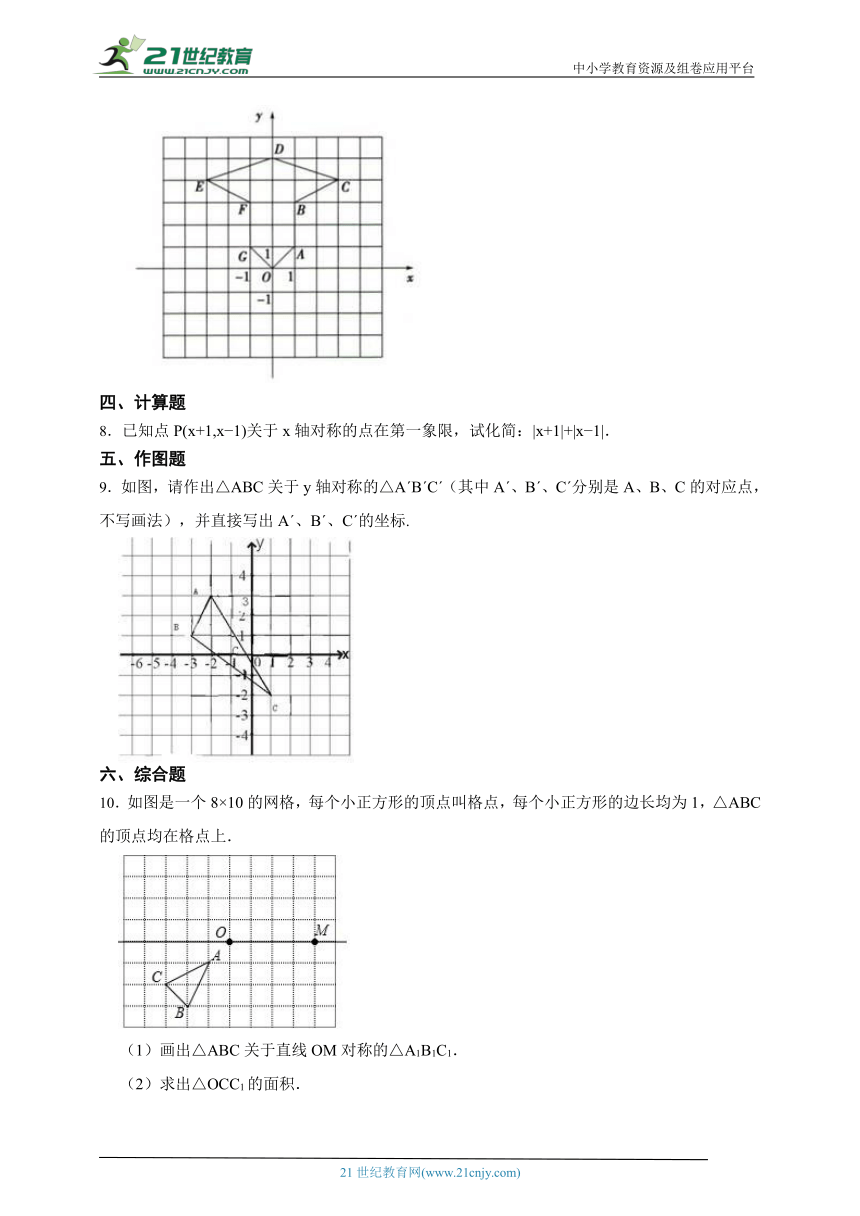
7.如图所示,写出图中点A,B,C,D,E,F,G的坐标,并比较点B与F,C与E,A与G的坐标特征,用文字表述出来.
四、计算题
8.已知点P(x+1,x 1)关于x轴对称的点在第一象限,试化简:|x+1|+|x 1|.
五、作图题
9.如图,请作出△ABC关于y轴对称的△A B C (其中A 、B 、C 分别是A、B、C的对应点,不写画法),并直接写出A 、B 、C 的坐标.
六、综合题
10.如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的△A1B1C1.
(2)求出△OCC1的面积.
答案解析部分
1.【答案】(-3,-2)
【解析】【解答】∵点A(3,-2)与点B关于y轴对称,
∴点B的坐标为(-3,-2).
【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变。即可得出答案。
2.【答案】A
【解析】【解答】解:点N(a,﹣b)关于x轴的对称点的坐标是(a,b),
故答案为:A.
【分析】根据关于x轴对称的点坐标的特征:纵坐标变为相反数,横坐标不变可得答案。
3.【答案】B
【解析】【分析】让横坐标相等,纵坐标互为相反数列式求值即可.
【解答】∵点A和点B关于x轴对称,
∴a=3,b+(-2)=0,
解得:a=3,b=2.
故选B.
4.【答案】D
【解析】【解答】解:点P(﹣3,2)关于x轴对称的点是(﹣3,﹣2),
故答案为:D.
【分析】根据关于x轴对称点的横坐标相同,纵坐标互为相反数可得.
5.【答案】C
【解析】【解答】解:∵点关于x轴的对称点在第二象限,
∴P点在第三象限,
∴,
解得:.
故答案为:C.
【分析】由题意易得P点在第三象限,进而根据第三象限的点,横坐标与纵坐标都是负数可列出不等式组,求解即可.
6.【答案】B
【解析】【解答】解:如图,左右对称的有4个,
如图,上下对称的有1个,
如图,关于正方形的对角线对称的有2个,
∴一共有7个与原三角形关于某直线对称的格点三角形.
故答案为:B.
【分析】把一个图形沿某一条直线折叠,如果这个图形能与另一个图形完全重合,那么这两个图形就关于这条直线对称,据此得出左右对称的有4个,上下对称的有1个,关于正方形的对角线对称的有2个,即可得出答案.
7.【答案】解:A(1,1),B(1,3),C(3,4),D(0,5),E(-3,4),F( 1,3), G(-1,1),点B与F,C与E,A与G都关于y轴对称.
【解析】【分析】在坐标系中分别读出各点的坐标,由于这三组点的坐标横坐标相等,纵坐标互为相反数, 可知点B与F,C与E,A与G都关于y轴对称.
8.【答案】解:∵点p(x+1, x-1)关于x轴对称的点在第一象限
∴点P在第四象限
∴x+1 >0,x-1<0
∴| x+1 |+| x-1 |=(x+1)-( x-1)= 2
【解析】【分析】关于x轴对称的点,横坐标相同,纵坐标互为相反数,可求出点P(x+1,x 1)关于x轴对称的点的坐标;在第一象限时,横坐标>0,纵坐标>0,因而就得到不等式组,解即可求得x的取值范围.再根据绝对值的性质化简即可.
9.【答案】解:
根据图形可得坐标:A′(2,3),B′(3,1),C′(-1,-2).
【解析】【分析】分别作出△ABC的三个顶点关于y轴的对称点,再顺次连接即可得到△A B C ,再根据所作的图形即可得到点A 、B 、C 的坐标.
10.【答案】(1)解:如图,△A1B1C1为所作;
(2)解:△OCC1的面积4×3=6.
【解析】【分析】(1)根据轴对称的性质分别确定点A、B、C关于直线OM对称的点A1、B1、C1,然后顺次连接即可;
(2)根据三角形的面积公式进行计算即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
13.2.2 用坐标表示轴对称一课一练
一、填空题
1.若点A(3,-2)与点B关于Y轴对称,则点B的坐标为 .
二、单选题
2.点N(a,﹣b)关于x轴的对称点的坐标是( )
A.(a,b) B.(﹣a,﹣b)
C.(-a,b) D.(﹣b,a)
3.已知点A(a,-2)和B(3,b)关于x轴对称,应当满足条件( )
A.a=2,b=3 B.a=3,b=2 C.a=-3,b=2 D.a=2,b=-3
4.和点P(﹣3,2)关于x轴对称的点是( )
A.(3,2) B.(﹣3,2)
C.(3,﹣2) D.(﹣3,﹣2)
5.已知点关于x轴的对称点在第二象限,则a的取值范围是( )
A. B. C. D.
6.如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A.6 B.7 C.8 D.9
三、解答题
7.如图所示,写出图中点A,B,C,D,E,F,G的坐标,并比较点B与F,C与E,A与G的坐标特征,用文字表述出来.
四、计算题
8.已知点P(x+1,x 1)关于x轴对称的点在第一象限,试化简:|x+1|+|x 1|.
五、作图题
9.如图,请作出△ABC关于y轴对称的△A B C (其中A 、B 、C 分别是A、B、C的对应点,不写画法),并直接写出A 、B 、C 的坐标.
六、综合题
10.如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的△A1B1C1.
(2)求出△OCC1的面积.
答案解析部分
1.【答案】(-3,-2)
【解析】【解答】∵点A(3,-2)与点B关于y轴对称,
∴点B的坐标为(-3,-2).
【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变。即可得出答案。
2.【答案】A
【解析】【解答】解:点N(a,﹣b)关于x轴的对称点的坐标是(a,b),
故答案为:A.
【分析】根据关于x轴对称的点坐标的特征:纵坐标变为相反数,横坐标不变可得答案。
3.【答案】B
【解析】【分析】让横坐标相等,纵坐标互为相反数列式求值即可.
【解答】∵点A和点B关于x轴对称,
∴a=3,b+(-2)=0,
解得:a=3,b=2.
故选B.
4.【答案】D
【解析】【解答】解:点P(﹣3,2)关于x轴对称的点是(﹣3,﹣2),
故答案为:D.
【分析】根据关于x轴对称点的横坐标相同,纵坐标互为相反数可得.
5.【答案】C
【解析】【解答】解:∵点关于x轴的对称点在第二象限,
∴P点在第三象限,
∴,
解得:.
故答案为:C.
【分析】由题意易得P点在第三象限,进而根据第三象限的点,横坐标与纵坐标都是负数可列出不等式组,求解即可.
6.【答案】B
【解析】【解答】解:如图,左右对称的有4个,
如图,上下对称的有1个,
如图,关于正方形的对角线对称的有2个,
∴一共有7个与原三角形关于某直线对称的格点三角形.
故答案为:B.
【分析】把一个图形沿某一条直线折叠,如果这个图形能与另一个图形完全重合,那么这两个图形就关于这条直线对称,据此得出左右对称的有4个,上下对称的有1个,关于正方形的对角线对称的有2个,即可得出答案.
7.【答案】解:A(1,1),B(1,3),C(3,4),D(0,5),E(-3,4),F( 1,3), G(-1,1),点B与F,C与E,A与G都关于y轴对称.
【解析】【分析】在坐标系中分别读出各点的坐标,由于这三组点的坐标横坐标相等,纵坐标互为相反数, 可知点B与F,C与E,A与G都关于y轴对称.
8.【答案】解:∵点p(x+1, x-1)关于x轴对称的点在第一象限
∴点P在第四象限
∴x+1 >0,x-1<0
∴| x+1 |+| x-1 |=(x+1)-( x-1)= 2
【解析】【分析】关于x轴对称的点,横坐标相同,纵坐标互为相反数,可求出点P(x+1,x 1)关于x轴对称的点的坐标;在第一象限时,横坐标>0,纵坐标>0,因而就得到不等式组,解即可求得x的取值范围.再根据绝对值的性质化简即可.
9.【答案】解:
根据图形可得坐标:A′(2,3),B′(3,1),C′(-1,-2).
【解析】【分析】分别作出△ABC的三个顶点关于y轴的对称点,再顺次连接即可得到△A B C ,再根据所作的图形即可得到点A 、B 、C 的坐标.
10.【答案】(1)解:如图,△A1B1C1为所作;
(2)解:△OCC1的面积4×3=6.
【解析】【分析】(1)根据轴对称的性质分别确定点A、B、C关于直线OM对称的点A1、B1、C1,然后顺次连接即可;
(2)根据三角形的面积公式进行计算即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
