对数函数(浙江省金华市磐安县)
文档属性
| 名称 | 对数函数(浙江省金华市磐安县) |
|
|
| 格式 | rar | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-10 00:00:00 | ||
图片预览

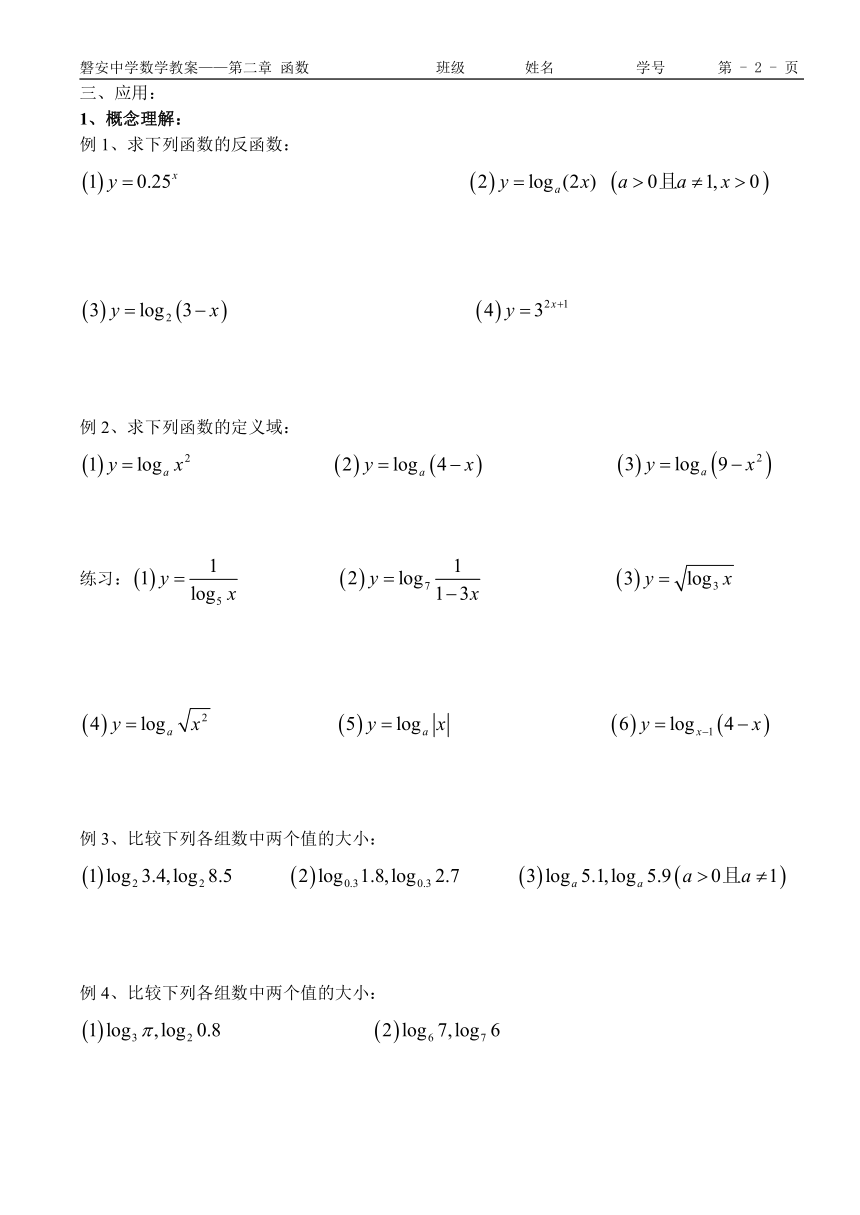


文档简介
磐安中学数学教案——第二章 函数 班级 姓名 学号 第 - 8 - 页
对数函数 ㈠
学习目标:
1、掌握对数函数的定义、图象和性质,把握指数函数与对数函数关系的实质;
2、能运用对数函数图象和性质来解决较为简单的问题;
学习重点、难点:对数函数的定义、图象和性质以及应用;
学习过程:
1、 引入:
1、求出与的反函数并画出其反函数的图象。
那么,指数函数的反函数是什么?
二、对数函数的图象与性质:
1、对数函数的定义: 。
2、①对数函数的定义域是 ;
②指数函数的定义域、值域与对数函数
的定义域、值域的关系:
③思考:
⑴观察所画图象,你能发现当时,有什么特征?当时,又有什么特征?这两种图象特征有何不同?
⑵根据图象特征,你能得出对数函数各有什么性质?它们有什么异同?
三、应用:
1、概念理解:
例1、求下列函数的反函数:
例2、求下列函数的定义域:
练习:
例3、比较下列各组数中两个值的大小:
例4、比较下列各组数中两个值的大小:
作业: 失误纠正:
一、选择题:
1、函数的定义域为( )
A、 B、 C、 D、
2、若,则a的取值范围是( )
A、 B、 C、 D、
3、函数的反函数是( )
A、 B、 C、 D、
4、函数的值域为( )
A、 B、 C、 D、
5、函数的定义域是( )
A、 B、 C、 D、
6、函数是( )
A、 在是增函数; B、在是减函数;
C、在是增函数; D、在是减函数;
二、填空题:
7、函数的值域是 。
8、函数与函数的图象关于 对称,
与函数的图象关于 对称,
与函数的图象关于 对称。
9、若的反函数是,则 .
10、用“<”,“>”,“≤”,“≥”填空:
①log36 log38; ②log 0.5 log 0.7; ③log2(x2+1) 0;
11、若定义域是[0,1],则的定义域是 ;
三、解答题 失误纠正:
12、将下列各数从小到大排列:
13、若,求x的取值范围。
14、设
(1)求证:为奇函数; (2)求的反函数。
对数函数(二)
学习目标:
1 能解对数函数不等式(方程),能求对数函数的单调区间。
2 能用对数函数的性质解题。
学习重点:对数函数的概念、图象、性质及应用。
一、知识回顾
1、函数 ( >0,且 )叫做对数函数。其定义域为 。
2、对数函数的图象和性质
二、例题讲解
㈠解对数不等式(方程):
例1.解不等式:
例2解方程:
㈡根据条件求底数、真数中字母的范围:
例3 (1) 已知 ,求a的取值范围. (2)已知,求a的取值范围。
(练习)已知,如果,那么x的取值范围是 。
㈢、求对数函数的单调区间:
例4、求下例函数的单调区间
(四)、其它
例5、已知函数
⑴求的定义域。 (2)当时,求时的取值范围。
例6、已知函数
⑴求的定义域 ⑵讨论的增减性。 ⑶当取何值时,函数的图象在轴右侧?
例7、已知函数
⑴若的定义域为R,求的取值范围。 ⑵若的值域为R,求的取值范围。
作业: 失误纠正:
1.函数是减函数,则实数的取值范围是( )
2.已知在是减函数,则的范围是
3.函数的定义域是 。
4.已知,则a的取值范围是
5.函数的单调递减区间是
6.不等式的解集是 。
7.不等式的解集是 。
8.方程的解是 。
9.方程的解是 。
10.函数的定义域为A,值域为B,则 。
11.求下列函数的单调区间:
(4)
12.已知函数 求该函数的定义域和值域。
证明:其函数图象关于直线对称.
13、已知函数的图象恒过定点P,求P点的坐标。
14、已知函数(其中a>0且)时,的最大值比最小值大2 . 求a的值 .
15、设函数,求满足的x值为多少?
PAGE
对数函数 ㈠
学习目标:
1、掌握对数函数的定义、图象和性质,把握指数函数与对数函数关系的实质;
2、能运用对数函数图象和性质来解决较为简单的问题;
学习重点、难点:对数函数的定义、图象和性质以及应用;
学习过程:
1、 引入:
1、求出与的反函数并画出其反函数的图象。
那么,指数函数的反函数是什么?
二、对数函数的图象与性质:
1、对数函数的定义: 。
2、①对数函数的定义域是 ;
②指数函数的定义域、值域与对数函数
的定义域、值域的关系:
③思考:
⑴观察所画图象,你能发现当时,有什么特征?当时,又有什么特征?这两种图象特征有何不同?
⑵根据图象特征,你能得出对数函数各有什么性质?它们有什么异同?
三、应用:
1、概念理解:
例1、求下列函数的反函数:
例2、求下列函数的定义域:
练习:
例3、比较下列各组数中两个值的大小:
例4、比较下列各组数中两个值的大小:
作业: 失误纠正:
一、选择题:
1、函数的定义域为( )
A、 B、 C、 D、
2、若,则a的取值范围是( )
A、 B、 C、 D、
3、函数的反函数是( )
A、 B、 C、 D、
4、函数的值域为( )
A、 B、 C、 D、
5、函数的定义域是( )
A、 B、 C、 D、
6、函数是( )
A、 在是增函数; B、在是减函数;
C、在是增函数; D、在是减函数;
二、填空题:
7、函数的值域是 。
8、函数与函数的图象关于 对称,
与函数的图象关于 对称,
与函数的图象关于 对称。
9、若的反函数是,则 .
10、用“<”,“>”,“≤”,“≥”填空:
①log36 log38; ②log 0.5 log 0.7; ③log2(x2+1) 0;
11、若定义域是[0,1],则的定义域是 ;
三、解答题 失误纠正:
12、将下列各数从小到大排列:
13、若,求x的取值范围。
14、设
(1)求证:为奇函数; (2)求的反函数。
对数函数(二)
学习目标:
1 能解对数函数不等式(方程),能求对数函数的单调区间。
2 能用对数函数的性质解题。
学习重点:对数函数的概念、图象、性质及应用。
一、知识回顾
1、函数 ( >0,且 )叫做对数函数。其定义域为 。
2、对数函数的图象和性质
二、例题讲解
㈠解对数不等式(方程):
例1.解不等式:
例2解方程:
㈡根据条件求底数、真数中字母的范围:
例3 (1) 已知 ,求a的取值范围. (2)已知,求a的取值范围。
(练习)已知,如果,那么x的取值范围是 。
㈢、求对数函数的单调区间:
例4、求下例函数的单调区间
(四)、其它
例5、已知函数
⑴求的定义域。 (2)当时,求时的取值范围。
例6、已知函数
⑴求的定义域 ⑵讨论的增减性。 ⑶当取何值时,函数的图象在轴右侧?
例7、已知函数
⑴若的定义域为R,求的取值范围。 ⑵若的值域为R,求的取值范围。
作业: 失误纠正:
1.函数是减函数,则实数的取值范围是( )
2.已知在是减函数,则的范围是
3.函数的定义域是 。
4.已知,则a的取值范围是
5.函数的单调递减区间是
6.不等式的解集是 。
7.不等式的解集是 。
8.方程的解是 。
9.方程的解是 。
10.函数的定义域为A,值域为B,则 。
11.求下列函数的单调区间:
(4)
12.已知函数 求该函数的定义域和值域。
证明:其函数图象关于直线对称.
13、已知函数的图象恒过定点P,求P点的坐标。
14、已知函数(其中a>0且)时,的最大值比最小值大2 . 求a的值 .
15、设函数,求满足的x值为多少?
PAGE
