华师大版七年级上数学5.1相交线试题
文档属性
| 名称 | 华师大版七年级上数学5.1相交线试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 408.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-13 00:00:00 | ||
图片预览




文档简介
试题解析(一)
对顶角的识别
1. 如图,在所标识的角中,互为对顶角的两个角是 ( )
A.∠2和∠3
B.∠1和∠3
C.∠1和∠4
D.∠1和∠2
【解析】选A.∠2和∠3有公共顶点,且∠2的两边与∠3的两边互为反向延长线. 2.下列说法正确的是 ( )
A.有公共顶点的两个角是对顶角
B.有公共顶点并且相等的两个角是对顶角
C.两条直线相交构成的四个角中任意两个角,不是邻补角就是对顶角
D.相等的两个角一定是对顶角
【解析】选C.有公共顶点且两边互为反向延 ( http: / / www.21cnjy.com )长线的两个角互为对顶角,故A,B错误,对顶角相等,但相等的角不一定是对顶角,两条直线相交构成的四个角中,有四对邻补角,两对对顶角.故选C.
3.如图,BE,CF相交于O,OA,OD是射线,其中构成对顶角的角是 .
( http: / / www.21cnjy.com )
【解析】根据对顶角的定义,构成对顶角的角是:∠EOF和∠BOC,∠EOC和∠BOF.
答案:∠EOF和∠BOC,∠EOC和∠BOF
4.如图,直线AB,CD,EF相交于点O,则图中对顶角共有 对.
( http: / / www.21cnjy.com )
【解析】图中对顶角有:∠AOF与∠BOE、 ( http: / / www.21cnjy.com )∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF,共6对.
答案:6
【易错提醒】角是由同一顶点出发的两条射线组 ( http: / / www.21cnjy.com )成的图形,多条直线相交于一点易漏数对顶角的对数.要注意多角度观察图形,按照一定的方法,找全所有的对顶角.
【方法技巧】从多条相交直线的图形中找对顶角的方法
按一定的顺序,比如从左到右 ( http: / / www.21cnjy.com ),以OA为边的角有∠AOF,∠AOD,找到其相应的对顶角,再找以OF为边的角∠FOD,∠FOB,找到其相应的对顶角,再找以OD为边的角∠DOB,∠DOE,找到其相应的对顶角.
对顶角的性质及其应用
1.(2014·芜湖模拟)下面四个图形中,∠1=∠2一定成立的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.选项B中∠1与∠2是对顶角,所以∠1=∠2.
2.(2013·湘西中考)如图,直线a和直线b相交于点O,∠1=50°,则
∠2= .
( http: / / www.21cnjy.com )
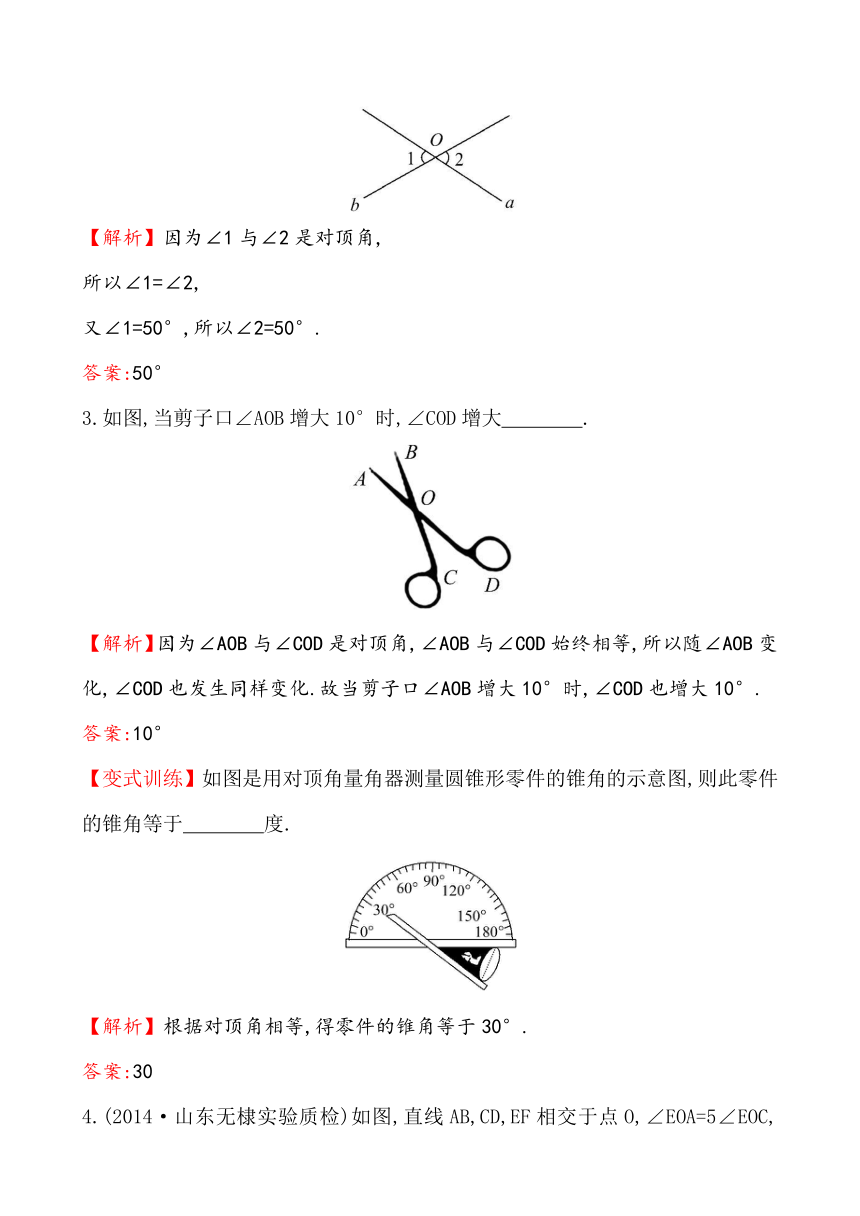
【解析】因为∠1与∠2是对顶角,
所以∠1=∠2,
又∠1=50°,所以∠2=50°.
答案:50°
3.如图,当剪子口∠AOB增大10°时,∠COD增大 .
( http: / / www.21cnjy.com )
【解析】因为∠AOB与∠COD是对顶角 ( http: / / www.21cnjy.com ),∠AOB与∠COD始终相等,所以随∠AOB变化,∠COD也发生同样变化.故当剪子口∠AOB增大10°时,∠COD也增大10°.
答案:10°
【变式训练】如图是用对顶角量角器测量圆锥形零件的锥角的示意图,则此零件的锥角等于 度.
( http: / / www.21cnjy.com )
【解析】根据对顶角相等,得零件的锥角等于30°.
答案:30
4.(2014·山东无棣实验质检)如图,直线AB,CD,EF相交于点O,∠EOA=5∠EOC,∠EOB=直角,则∠AOD= ,∠BOF= ,∠AOC= .
( http: / / www.21cnjy.com )
【解析】∠EOB=直角=45°,
所以∠EOA=180°-45°=135°,
所以∠BOF=∠EOA=135°,
因为∠EOA=5∠EOC,
所以∠EOC=27°,
所以∠AOC=135°-27°=108°,
∠BOC=45°+27°=72°,
所以∠AOD=72°.
答案:72° 135° 108°
【知识归纳】对顶角的三个用途
(1)利用对顶角的定义来辨析:识别 ( http: / / www.21cnjy.com )两个角是否为对顶角,一要看这两个角是否由两条直线相交得到的,二要看这两个角是不是有公共顶点而没有公共边.只有同时满足这两个条件时,才能断定这两个角是对顶角.
(2)利用对顶角的性质来计算:两条 ( http: / / www.21cnjy.com )直线交于一点,一定会出现对顶角、平角与互补的角,解题中要充分利用它们的性质,搭起已知角与未知角之间的桥梁.
(3)利用对顶角的性质来说理:今后经常利用对顶角的性质、角平分线的性质及互余、互补的性质等进行说理.
5.如图,直线a,b相交.
(1)已知∠1=40°,求∠2,∠3,∠4.
(2)已知∠2+∠4=280°,求各角.
(3)已知∠1∶∠2=2∶7,求各角.
【解析】(1)因为∠1与∠3为对顶角,故∠3=∠1=40°,
因为∠1与∠2,∠1与∠4是邻补角,所以∠1+∠2=180°,
∠1+∠4=180°,所以∠2=180°-∠1=180°-40°=140°,
∠4=180°-∠1=180°-40°=140°.
(2)因为∠2与∠4为对顶角,故∠2=∠4,
又因为∠2+∠4=280°,
所以∠2=∠4=140°,∠1=∠3=180°-140°=40°.
(3)设∠1=2x,∠2=7x,
因为∠1+∠2=180°,
即2x+7x=180°,x=20°,
所以∠1=∠3=2x=40°,∠2=∠4=7x=140°.
6.如图,直线AB,CD相交于点O,OE平分∠BOD,∠DOE=15°,求∠AOC,∠BOC的度数.
( http: / / www.21cnjy.com )
【解析】因为OE平分∠BOD,所以∠BOD=2∠DOE=2×15°=30°.
∠AOC与∠BOD互为对顶角,故∠AOC=∠BOD=30°,
∠BOC与∠AOC互补,所以∠BOC=180°-∠AOC=150°.
【错在哪?】作业错例 课堂实拍
如图,直线CD,EF相交于点O,OA平分∠EOC,OB平分∠DOF,∠COF=150°,
试说明∠AOB是平角.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案:(1)③
(2) 因为∠COE与∠DOF是对顶角,所以∠COE=∠DOF=30°,因为OB平分∠DOF,所以∠BOF=∠BOD=∠DOF=15°,∠AOB=∠AOC+∠COF+∠BOF=15°+150°+15°=180°.即∠AOB是平角.
试题解析(二)
垂线的作法及其计算
1.(2013·浙江湖州六校联考)如图,直线AB与CD相交于点O,EO⊥AB,则∠1与∠2 ( )
( http: / / www.21cnjy.com )
A.是对顶角 B.相等
C.互余 D.互补
【解析】选C.因为EO⊥AB,则∠AOE=90°,则∠1+∠2=180°-∠AOE=90°,所以∠1与∠2互余.
2.数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的有 ( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
【解析】选D.从左向右第一个图形中,BE不是 ( http: / / www.21cnjy.com )线段;第二个图形中,BE不垂直于AC;第三个图形中,是过点E作的AC的垂线段;第四个图形是过点E作的BC的垂线段.综上所述4个都不正确.
3.(2014·东北师大附中质检)如图,∠AOB=∠COD=90°,∠BOC=42°,则∠AOD等于 ( )
( http: / / www.21cnjy.com )
A.48° B.148° C.138° D.128°
【解析】选C.∠AOD=360°-∠AOB-∠COD-∠BOC
=360°-90°-90°-42°=138°.
【互动探究】∠BOC与∠AOD有什么关系
【解析】因为周角为360° ( http: / / www.21cnjy.com ),所以∠AOD+∠BOC=360°-∠AOB-∠COD=360°-90°-90°=180°,故∠BOC与∠AOD互补.
【知识归纳】两角互补与互余
1.两个角的和等于90°,则两角互余;互余的性质:同角或等角的余角相等.
2.两个角的和等于180°,则两角互补;互补的性质:同角或等角的补角相等.
4.同一平面内直线l与线段AB,若l⊥AB,下列说法正确的是 ( )
A.没有公共点
B.只有一个公共点
C.有一个公共点或没有公共点
D.以上都不对
【解析】选C.直线和线段垂直,指的是直线与线段所在的直线垂直,所以直线l与线段有一个公共点或没有公共点.
5.(2013·普洱中考)如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为 .
( http: / / www.21cnjy.com )
【解析】因为AB⊥CD,所以∠ABD=90°;又因为EF平分∠ABD,所以∠DBE=
∠ABD=45°,∠CBF=∠DBE=45°.
答案:45°
6.如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,则点B到直线AC的距离等于 ;CD是点 到 的垂线段.
【解析】根据垂线段、点到直线的距离的定义可知,点B到直线AC的距离等于BC的长度,即为4.线段CD是点C到直线AB的垂线段.
答案:4 C 直线AB
【易错提醒】垂线是一条直线,而垂线段是一条线段.而点到直线的距离是指垂线段的长度.
【知识归纳】“点到直线的距离”与“两点间的距离”的联系
1.点到直线的距离是点到直线的垂线段的长度,过这个点作垂线找到垂足后,再度量长度即可,点到直线的距离的概念中隐含着极其重要的两个字:垂直.
2.两点间的距离是连结两点的线段的长度,只要连结两点,再度量其长度即可,与垂直无关.
7.如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
( http: / / www.21cnjy.com )
(1)∠AOC与∠BOD相等吗 为什么
(2)若∠BOD=32°,求∠AOE的度数.
【解析】(1)相等.因为OA⊥OB,OC⊥OD,OE是OD的反向延长线,
所以∠AOB=90°,∠COD=∠COE=90°.
所以∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∠AOC=∠BOD.
(2)因为∠BOD=32°,由(1)知,∠AOC=∠BOD=32°,
所以∠AOE=∠COE-∠AOC=90°-32°=58°.
垂线的性质及其应用
1.如图所示,PO⊥OB ( http: / / www.21cnjy.com ),OC⊥PB,OP=3cm,OB=2cm,则点B到OP的距离是 cm,点P到OB的距离是 cm,OB,OC,OP三条线段中, 最短,理由是 .
【解析】由点到直线的距离以及“垂线段最短”这一性质可得出答案.
答案:2 3 OC 垂线段最短
2.如图,某人站在公路左侧A处,要到公路右侧,怎样走最近 为什么 若他要到路对面的B处,怎样走最近 说明理由.
( http: / / www.21cnjy.com )
【解题指南】解答本题的两个关键:
1.将实际问题转化为数学问题.
2.垂线段最短与两点之间线段最短的结论.
【解析】某人在路的左侧A处,要到路的右侧,如图,沿垂线AC的方向走最近,根据垂线段最短.
( http: / / www.21cnjy.com )
若他要到路对面的B处,如图,连结AB,沿线段AB走最近,根据两点之间线段最短.
3.如图,要只挖一条水渠把水送到A,B两地,请你设计一条最短的路线,在图上画出来并说明理由.
( http: / / www.21cnjy.com )
【解析】连结AB,过点B作BP⊥l.
( http: / / www.21cnjy.com )
路线为A-B-P.
由A地经过B地,根据两点之间线段最短;
点B到河岸的最短距离为点B到直线l的垂线段的长度.
【互动探究】如果把“只挖一条水渠”改为“挖两条水渠”请你分别设计最短的路线.
【解析】过点A作AQ⊥l,过点B作BP⊥l,如图:
( http: / / www.21cnjy.com )
由A到l的最短距离为AQ,由B到l的最短距离为BP.
【知识归纳】解决“平面上最短问题”的两把钥匙
1.两点之间,线段最短.
2.垂线段最短.
【错在哪?】作业错例 课堂实拍
若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为
( )
A.10cm B.4cm
C.10cm或4cm D.至少4cm
试题解析(三)
同位角、内错角、同旁内角的识别
1.下图中,∠1和∠2是同位角的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.选项A,B,C中的∠1,∠2的两边都不在同一条直线上,不是同位角;
选项D中的∠1,∠2有一边在同一条直线上,
又在被截线的同一方,是同位角.
【变式训练】图中所标出的角中,共有同位角 ( )
( http: / / www.21cnjy.com )
A.2对 B.3对 C.4对 D.5对
【解析】选D.根据同位角的定义,图中∠3与∠4,∠4与∠5,∠7与∠1,∠5与
∠2,∠2与∠3是同位角,共5对.
2.如图,∠1和∠2是 和 被 所截的
角.∠3和∠4是 和 被 所截
的 角.
【解析】因为∠1和∠2均有一条边在直线 ( http: / / www.21cnjy.com )AC上,故AC为截线,∠1和∠2的另一边分别为AB和CD,故为被截线.同理∠3和∠4是直线AD和BC被直线AC所截的内错角.
答案:AB CD AC 内错 AD BC AC 内错
【方法技巧】找同位角、内错角、同旁内角的方法
(1)在截线的同旁,找同位角和同旁内角,在截线的两侧,找内错角.
(2)位置相同的一对角为同位角,在内部被交错的一对角称为内错角,在内部且同旁的一对角称为同旁内角.
3.写出图中数字表示的角哪些是同位角 哪些是内错角 哪些是同旁内角
( http: / / www.21cnjy.com )
【解析】同位角有∠1和∠3,∠5和∠6,内错角有∠2和∠4,∠1和∠6,同旁内角有∠1和∠5,∠2和∠6,∠3和∠4,∠3和∠5.
【易错提醒】要在复杂的图形中,找出基本图形,根据同位角、内错角、同旁内角的位置关系,找出所有的同位角、内错角、同旁内角,不要漏掉或认错.
【方法技巧】怎样防止找错或遗漏
1.在复杂的图形中,角过多,往往顾此失彼,为避免遗漏,在寻找的过程中,先从最小数字的角开始,把与它有关的角都找出来,依次类推就不会遗漏.
2.在找角的过程中,产生认错的原因是没 ( http: / / www.21cnjy.com )有掌握好三种角的位置关系,在复杂图形中,辨认两个角的位置关系,先要弄清哪条直线是截线,哪条直线为被截线.
4.如图,(1)DE为截线,∠E与哪个角是同位角
(2)∠B与∠4是同旁内角,则截出这两个角的截线与被截线是哪几条直线
(3)∠B和∠E是同位角吗 为什么
【解析】(1)∠E与∠3是同位角.
(2)截出这两个角的截线是直线BC,被截线是直线AB,ED.
(3)不是.因为∠B与∠E的边中没有一条落在同一直线上,所以∠B与∠E不是同位角.
5.如图,以点C为顶点,在△ABC外画∠ACE=∠A,且点A和点E在直线BC的同侧,再延长BC至D,回答下列问题:
(1)∠A与哪些角是内错角
(2)∠B与哪些角是同位角
(3)∠ACB与哪些角是同旁内角
【解析】(1)∠A的两边是AB和A ( http: / / www.21cnjy.com )C,找∠A的内错角,只能是AC为截线,与AC相交的线有两条:CD与CE,所以与∠A成内错角的为∠DCA,∠ACE.
(2)∠B的两边为AB和BC,找∠B的同 ( http: / / www.21cnjy.com )位角,只能BC作截线,与BC相交的线有两条:AC和CE,所以∠B的同位角有两个,为∠DCE和∠ACD.
(3)∠ACB的两边是AC和BC,找∠ACB的同旁内角,AC和BC都可以作截线,∠ACB的同旁内角有两个,为∠BAC和∠ABC.
6.两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角,若
∠1=3∠2,∠2=3∠3,求∠1,∠2的度数.
( http: / / www.21cnjy.com )
【解析】如图,由于∠1=3∠2,
∠2=3∠3,
所以∠1=3×3∠3=9∠3,
又因为∠1+∠3=180°,
所以∠1=180°×=162°,∠2=∠1=54°.
【错在哪?】作业错例 课堂实拍
如图,与∠2互为同旁内角的角共有 ( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案:(1)①
(2)没考虑全面,当直线AB,BC被直线AC所截时,与∠2互为同旁内角的是∠BAC,故与∠2互为同旁内角的有3个,选C.
对顶角的识别
1. 如图,在所标识的角中,互为对顶角的两个角是 ( )
A.∠2和∠3
B.∠1和∠3
C.∠1和∠4
D.∠1和∠2
【解析】选A.∠2和∠3有公共顶点,且∠2的两边与∠3的两边互为反向延长线. 2.下列说法正确的是 ( )
A.有公共顶点的两个角是对顶角
B.有公共顶点并且相等的两个角是对顶角
C.两条直线相交构成的四个角中任意两个角,不是邻补角就是对顶角
D.相等的两个角一定是对顶角
【解析】选C.有公共顶点且两边互为反向延 ( http: / / www.21cnjy.com )长线的两个角互为对顶角,故A,B错误,对顶角相等,但相等的角不一定是对顶角,两条直线相交构成的四个角中,有四对邻补角,两对对顶角.故选C.
3.如图,BE,CF相交于O,OA,OD是射线,其中构成对顶角的角是 .
( http: / / www.21cnjy.com )
【解析】根据对顶角的定义,构成对顶角的角是:∠EOF和∠BOC,∠EOC和∠BOF.
答案:∠EOF和∠BOC,∠EOC和∠BOF
4.如图,直线AB,CD,EF相交于点O,则图中对顶角共有 对.
( http: / / www.21cnjy.com )
【解析】图中对顶角有:∠AOF与∠BOE、 ( http: / / www.21cnjy.com )∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF,共6对.
答案:6
【易错提醒】角是由同一顶点出发的两条射线组 ( http: / / www.21cnjy.com )成的图形,多条直线相交于一点易漏数对顶角的对数.要注意多角度观察图形,按照一定的方法,找全所有的对顶角.
【方法技巧】从多条相交直线的图形中找对顶角的方法
按一定的顺序,比如从左到右 ( http: / / www.21cnjy.com ),以OA为边的角有∠AOF,∠AOD,找到其相应的对顶角,再找以OF为边的角∠FOD,∠FOB,找到其相应的对顶角,再找以OD为边的角∠DOB,∠DOE,找到其相应的对顶角.
对顶角的性质及其应用
1.(2014·芜湖模拟)下面四个图形中,∠1=∠2一定成立的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.选项B中∠1与∠2是对顶角,所以∠1=∠2.
2.(2013·湘西中考)如图,直线a和直线b相交于点O,∠1=50°,则
∠2= .
( http: / / www.21cnjy.com )
【解析】因为∠1与∠2是对顶角,
所以∠1=∠2,
又∠1=50°,所以∠2=50°.
答案:50°
3.如图,当剪子口∠AOB增大10°时,∠COD增大 .
( http: / / www.21cnjy.com )
【解析】因为∠AOB与∠COD是对顶角 ( http: / / www.21cnjy.com ),∠AOB与∠COD始终相等,所以随∠AOB变化,∠COD也发生同样变化.故当剪子口∠AOB增大10°时,∠COD也增大10°.
答案:10°
【变式训练】如图是用对顶角量角器测量圆锥形零件的锥角的示意图,则此零件的锥角等于 度.
( http: / / www.21cnjy.com )
【解析】根据对顶角相等,得零件的锥角等于30°.
答案:30
4.(2014·山东无棣实验质检)如图,直线AB,CD,EF相交于点O,∠EOA=5∠EOC,∠EOB=直角,则∠AOD= ,∠BOF= ,∠AOC= .
( http: / / www.21cnjy.com )
【解析】∠EOB=直角=45°,
所以∠EOA=180°-45°=135°,
所以∠BOF=∠EOA=135°,
因为∠EOA=5∠EOC,
所以∠EOC=27°,
所以∠AOC=135°-27°=108°,
∠BOC=45°+27°=72°,
所以∠AOD=72°.
答案:72° 135° 108°
【知识归纳】对顶角的三个用途
(1)利用对顶角的定义来辨析:识别 ( http: / / www.21cnjy.com )两个角是否为对顶角,一要看这两个角是否由两条直线相交得到的,二要看这两个角是不是有公共顶点而没有公共边.只有同时满足这两个条件时,才能断定这两个角是对顶角.
(2)利用对顶角的性质来计算:两条 ( http: / / www.21cnjy.com )直线交于一点,一定会出现对顶角、平角与互补的角,解题中要充分利用它们的性质,搭起已知角与未知角之间的桥梁.
(3)利用对顶角的性质来说理:今后经常利用对顶角的性质、角平分线的性质及互余、互补的性质等进行说理.
5.如图,直线a,b相交.
(1)已知∠1=40°,求∠2,∠3,∠4.
(2)已知∠2+∠4=280°,求各角.
(3)已知∠1∶∠2=2∶7,求各角.
【解析】(1)因为∠1与∠3为对顶角,故∠3=∠1=40°,
因为∠1与∠2,∠1与∠4是邻补角,所以∠1+∠2=180°,
∠1+∠4=180°,所以∠2=180°-∠1=180°-40°=140°,
∠4=180°-∠1=180°-40°=140°.
(2)因为∠2与∠4为对顶角,故∠2=∠4,
又因为∠2+∠4=280°,
所以∠2=∠4=140°,∠1=∠3=180°-140°=40°.
(3)设∠1=2x,∠2=7x,
因为∠1+∠2=180°,
即2x+7x=180°,x=20°,
所以∠1=∠3=2x=40°,∠2=∠4=7x=140°.
6.如图,直线AB,CD相交于点O,OE平分∠BOD,∠DOE=15°,求∠AOC,∠BOC的度数.
( http: / / www.21cnjy.com )
【解析】因为OE平分∠BOD,所以∠BOD=2∠DOE=2×15°=30°.
∠AOC与∠BOD互为对顶角,故∠AOC=∠BOD=30°,
∠BOC与∠AOC互补,所以∠BOC=180°-∠AOC=150°.
【错在哪?】作业错例 课堂实拍
如图,直线CD,EF相交于点O,OA平分∠EOC,OB平分∠DOF,∠COF=150°,
试说明∠AOB是平角.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案:(1)③
(2) 因为∠COE与∠DOF是对顶角,所以∠COE=∠DOF=30°,因为OB平分∠DOF,所以∠BOF=∠BOD=∠DOF=15°,∠AOB=∠AOC+∠COF+∠BOF=15°+150°+15°=180°.即∠AOB是平角.
试题解析(二)
垂线的作法及其计算
1.(2013·浙江湖州六校联考)如图,直线AB与CD相交于点O,EO⊥AB,则∠1与∠2 ( )
( http: / / www.21cnjy.com )
A.是对顶角 B.相等
C.互余 D.互补
【解析】选C.因为EO⊥AB,则∠AOE=90°,则∠1+∠2=180°-∠AOE=90°,所以∠1与∠2互余.
2.数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的有 ( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
【解析】选D.从左向右第一个图形中,BE不是 ( http: / / www.21cnjy.com )线段;第二个图形中,BE不垂直于AC;第三个图形中,是过点E作的AC的垂线段;第四个图形是过点E作的BC的垂线段.综上所述4个都不正确.
3.(2014·东北师大附中质检)如图,∠AOB=∠COD=90°,∠BOC=42°,则∠AOD等于 ( )
( http: / / www.21cnjy.com )
A.48° B.148° C.138° D.128°
【解析】选C.∠AOD=360°-∠AOB-∠COD-∠BOC
=360°-90°-90°-42°=138°.
【互动探究】∠BOC与∠AOD有什么关系
【解析】因为周角为360° ( http: / / www.21cnjy.com ),所以∠AOD+∠BOC=360°-∠AOB-∠COD=360°-90°-90°=180°,故∠BOC与∠AOD互补.
【知识归纳】两角互补与互余
1.两个角的和等于90°,则两角互余;互余的性质:同角或等角的余角相等.
2.两个角的和等于180°,则两角互补;互补的性质:同角或等角的补角相等.
4.同一平面内直线l与线段AB,若l⊥AB,下列说法正确的是 ( )
A.没有公共点
B.只有一个公共点
C.有一个公共点或没有公共点
D.以上都不对
【解析】选C.直线和线段垂直,指的是直线与线段所在的直线垂直,所以直线l与线段有一个公共点或没有公共点.
5.(2013·普洱中考)如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为 .
( http: / / www.21cnjy.com )
【解析】因为AB⊥CD,所以∠ABD=90°;又因为EF平分∠ABD,所以∠DBE=
∠ABD=45°,∠CBF=∠DBE=45°.
答案:45°
6.如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,则点B到直线AC的距离等于 ;CD是点 到 的垂线段.
【解析】根据垂线段、点到直线的距离的定义可知,点B到直线AC的距离等于BC的长度,即为4.线段CD是点C到直线AB的垂线段.
答案:4 C 直线AB
【易错提醒】垂线是一条直线,而垂线段是一条线段.而点到直线的距离是指垂线段的长度.
【知识归纳】“点到直线的距离”与“两点间的距离”的联系
1.点到直线的距离是点到直线的垂线段的长度,过这个点作垂线找到垂足后,再度量长度即可,点到直线的距离的概念中隐含着极其重要的两个字:垂直.
2.两点间的距离是连结两点的线段的长度,只要连结两点,再度量其长度即可,与垂直无关.
7.如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
( http: / / www.21cnjy.com )
(1)∠AOC与∠BOD相等吗 为什么
(2)若∠BOD=32°,求∠AOE的度数.
【解析】(1)相等.因为OA⊥OB,OC⊥OD,OE是OD的反向延长线,
所以∠AOB=90°,∠COD=∠COE=90°.
所以∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∠AOC=∠BOD.
(2)因为∠BOD=32°,由(1)知,∠AOC=∠BOD=32°,
所以∠AOE=∠COE-∠AOC=90°-32°=58°.
垂线的性质及其应用
1.如图所示,PO⊥OB ( http: / / www.21cnjy.com ),OC⊥PB,OP=3cm,OB=2cm,则点B到OP的距离是 cm,点P到OB的距离是 cm,OB,OC,OP三条线段中, 最短,理由是 .
【解析】由点到直线的距离以及“垂线段最短”这一性质可得出答案.
答案:2 3 OC 垂线段最短
2.如图,某人站在公路左侧A处,要到公路右侧,怎样走最近 为什么 若他要到路对面的B处,怎样走最近 说明理由.
( http: / / www.21cnjy.com )
【解题指南】解答本题的两个关键:
1.将实际问题转化为数学问题.
2.垂线段最短与两点之间线段最短的结论.
【解析】某人在路的左侧A处,要到路的右侧,如图,沿垂线AC的方向走最近,根据垂线段最短.
( http: / / www.21cnjy.com )
若他要到路对面的B处,如图,连结AB,沿线段AB走最近,根据两点之间线段最短.
3.如图,要只挖一条水渠把水送到A,B两地,请你设计一条最短的路线,在图上画出来并说明理由.
( http: / / www.21cnjy.com )
【解析】连结AB,过点B作BP⊥l.
( http: / / www.21cnjy.com )
路线为A-B-P.
由A地经过B地,根据两点之间线段最短;
点B到河岸的最短距离为点B到直线l的垂线段的长度.
【互动探究】如果把“只挖一条水渠”改为“挖两条水渠”请你分别设计最短的路线.
【解析】过点A作AQ⊥l,过点B作BP⊥l,如图:
( http: / / www.21cnjy.com )
由A到l的最短距离为AQ,由B到l的最短距离为BP.
【知识归纳】解决“平面上最短问题”的两把钥匙
1.两点之间,线段最短.
2.垂线段最短.
【错在哪?】作业错例 课堂实拍
若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为
( )
A.10cm B.4cm
C.10cm或4cm D.至少4cm
试题解析(三)
同位角、内错角、同旁内角的识别
1.下图中,∠1和∠2是同位角的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.选项A,B,C中的∠1,∠2的两边都不在同一条直线上,不是同位角;
选项D中的∠1,∠2有一边在同一条直线上,
又在被截线的同一方,是同位角.
【变式训练】图中所标出的角中,共有同位角 ( )
( http: / / www.21cnjy.com )
A.2对 B.3对 C.4对 D.5对
【解析】选D.根据同位角的定义,图中∠3与∠4,∠4与∠5,∠7与∠1,∠5与
∠2,∠2与∠3是同位角,共5对.
2.如图,∠1和∠2是 和 被 所截的
角.∠3和∠4是 和 被 所截
的 角.
【解析】因为∠1和∠2均有一条边在直线 ( http: / / www.21cnjy.com )AC上,故AC为截线,∠1和∠2的另一边分别为AB和CD,故为被截线.同理∠3和∠4是直线AD和BC被直线AC所截的内错角.
答案:AB CD AC 内错 AD BC AC 内错
【方法技巧】找同位角、内错角、同旁内角的方法
(1)在截线的同旁,找同位角和同旁内角,在截线的两侧,找内错角.
(2)位置相同的一对角为同位角,在内部被交错的一对角称为内错角,在内部且同旁的一对角称为同旁内角.
3.写出图中数字表示的角哪些是同位角 哪些是内错角 哪些是同旁内角
( http: / / www.21cnjy.com )
【解析】同位角有∠1和∠3,∠5和∠6,内错角有∠2和∠4,∠1和∠6,同旁内角有∠1和∠5,∠2和∠6,∠3和∠4,∠3和∠5.
【易错提醒】要在复杂的图形中,找出基本图形,根据同位角、内错角、同旁内角的位置关系,找出所有的同位角、内错角、同旁内角,不要漏掉或认错.
【方法技巧】怎样防止找错或遗漏
1.在复杂的图形中,角过多,往往顾此失彼,为避免遗漏,在寻找的过程中,先从最小数字的角开始,把与它有关的角都找出来,依次类推就不会遗漏.
2.在找角的过程中,产生认错的原因是没 ( http: / / www.21cnjy.com )有掌握好三种角的位置关系,在复杂图形中,辨认两个角的位置关系,先要弄清哪条直线是截线,哪条直线为被截线.
4.如图,(1)DE为截线,∠E与哪个角是同位角
(2)∠B与∠4是同旁内角,则截出这两个角的截线与被截线是哪几条直线
(3)∠B和∠E是同位角吗 为什么
【解析】(1)∠E与∠3是同位角.
(2)截出这两个角的截线是直线BC,被截线是直线AB,ED.
(3)不是.因为∠B与∠E的边中没有一条落在同一直线上,所以∠B与∠E不是同位角.
5.如图,以点C为顶点,在△ABC外画∠ACE=∠A,且点A和点E在直线BC的同侧,再延长BC至D,回答下列问题:
(1)∠A与哪些角是内错角
(2)∠B与哪些角是同位角
(3)∠ACB与哪些角是同旁内角
【解析】(1)∠A的两边是AB和A ( http: / / www.21cnjy.com )C,找∠A的内错角,只能是AC为截线,与AC相交的线有两条:CD与CE,所以与∠A成内错角的为∠DCA,∠ACE.
(2)∠B的两边为AB和BC,找∠B的同 ( http: / / www.21cnjy.com )位角,只能BC作截线,与BC相交的线有两条:AC和CE,所以∠B的同位角有两个,为∠DCE和∠ACD.
(3)∠ACB的两边是AC和BC,找∠ACB的同旁内角,AC和BC都可以作截线,∠ACB的同旁内角有两个,为∠BAC和∠ABC.
6.两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角,若
∠1=3∠2,∠2=3∠3,求∠1,∠2的度数.
( http: / / www.21cnjy.com )
【解析】如图,由于∠1=3∠2,
∠2=3∠3,
所以∠1=3×3∠3=9∠3,
又因为∠1+∠3=180°,
所以∠1=180°×=162°,∠2=∠1=54°.
【错在哪?】作业错例 课堂实拍
如图,与∠2互为同旁内角的角共有 ( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案:(1)①
(2)没考虑全面,当直线AB,BC被直线AC所截时,与∠2互为同旁内角的是∠BAC,故与∠2互为同旁内角的有3个,选C.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
