三 角 形 的 边

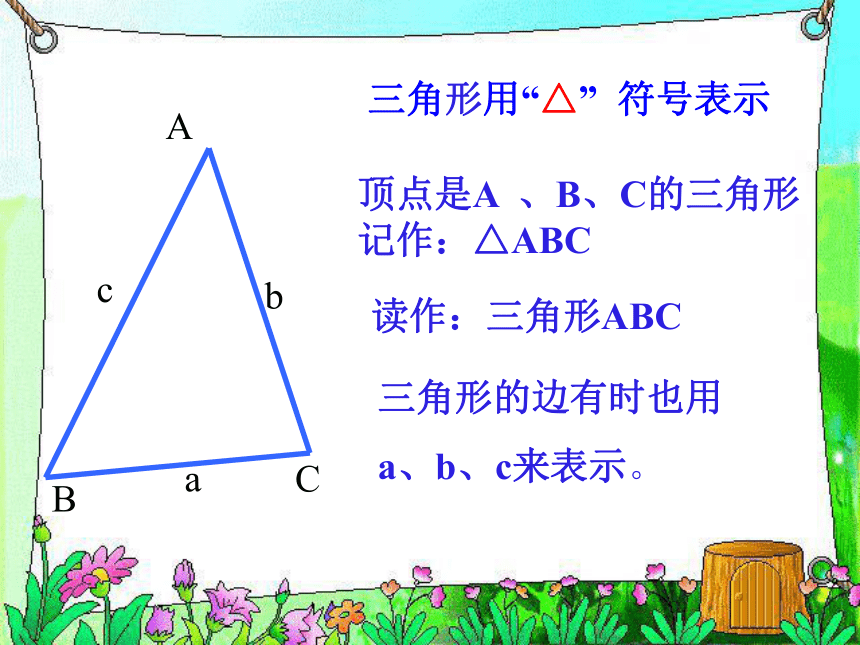
课件32张PPT。你能举出生活中三角形的例子吗？ 由不在同一直线上的三条线段首尾 顺次相接所组成的图形叫做三角形ACB1.AB、BC、CA叫做三角形的边2.点A、B、C叫做三角形的顶点3.∠ A、 ∠ B、 ∠ C叫做三角形的内角，简称三角形的角。ACB顶点是A 、B、C的三角形 记作：△ABCacb读作：三角形ABC三角形的边有时也用
a、b、c来表示。三角形用“△” 符号表示判断:以下哪些属于三角形?ABCD1.图中有几个三角形？用符号表示这些三角形。2.以AB为边的三角形有哪些？△ABC、△ABE3.以E为顶点的三角形有哪些？△ ABE 、△BCE、 △CDE小试牛刀4.以∠D为角的三角形有哪些？△ BCD、 △DEC议一议： 在B点的小狗，为了尽快吃到A点的香肠，它会选择哪条路线?
CBA在一个三角形中，任意两边之和与第三边的长度有怎样的关系？为什么？做一做：在一个三角形中，任意两边之差与第三边的长度有怎样的关系？任意画一个三角形,量出三条边的长度,求出任意两条边的长度差,和第三边进行比较,你有什么发现?三角形两边之和大于第三边三角形三边关系三角形两边之差小于第三边某村庄和小学分别位于两条交叉的大路边（如图）。可是，每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢？麦田请用所学的数学知识解释：三角形任意两边之和大于第三边为什么经常有行人斜穿马路而不走人行横道？只要满足较小的两条线段之和大于第三条线段，便可构成三角形;若不满足，则不能构成三角形.下列长度的各组线段能否组成一个三角形？
（1）15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练较小两边之和大于第三边,才能构成三角形1.下列长度的三条线段能否组成三角形？为什么？（1） 3，4，8 （ ）
（2） 2，5，6 （ ）
（3） 5，6，10 （ ）
（4） 2，5，8 （ ）不能能能不能再练一练试一试2.小颖要制作一个三角形木架，现有两根长度为8cm和5cm的木棒，如果要求第三根木棒的长度是偶数，小颖有几种选法？第三根的长度可以是多少？小颖有5种选法。第三根木棒的长度可以是：4cm，6cm，8cm，10cm，12cm通过本节课的学习，你有哪些收获？ 1.三角形的边、角、顶点, 表示方法；
2.三角形三边关系及运用.1、已知两条线段的长分别是3cm、5cm ，
要想拼成一个三角形，问第三条线段a应
取的范围是多少？ 试一试 2、已知两条线段的长分别是3cm、5cm ，
要想拼成一个三角形，且第三条线段a的
长为奇数，问第三条线段应取多少长？ 2cm两边之差＜第三边＜两边之和2、已知两条边长分别为2cm、5cm，
你可以画出几个符合条件的等腰三角形？做一做1、已知两条边长分别为3cm、5cm，你可以
画出几个符合条件的等腰三角形？并求符合
条件的等腰三角形的周长. (3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边，可构成_____个三角形．摘苹果（1）任何三条线段都能组成一个三角形 ( ) （2）因为a+b>c,所以a、b、c三边可以构成三角形（ ）（4）已知等腰三角形的两边长分别为8cm，3cm，
则这三角形的周长为 （　 ）　　（A） 14cm　 （B）19cm
（C） 14cm或19cm （D） 不确定××2B草原上的四口油井，位于如图所示的A、B、C、D四个位置，现在要建立一个维修站H，问H建在何处，才能使它到四个油井的距离之和HA+HB＋HC+HD为最小？说明理由。拓展与应用！ADCBHH′1.你认为这个H应该在什么位置？大胆设想！2.到AC最近的点在哪儿？到BD?看谁最聪明！作业：课本P75：1，2。
按角分锐角三角形直角三角形钝角三角形
按边分不等边三角形（不规则三角形）等腰三角形三角形的分类只有两条边相等的等腰三角形等边三角形用长度分别为7cm、8cm、12cm、16cm的四根木棒，取其中三根搭成三角形。哪些能，哪些不能？你能搭成几个三角形？
7cm8cm12cm7cm8cm16cm7cm12cm16cm8cm12cm16cm能你发现三角形的边之间有何关系？能能不能探究
智力大冲浪用3根长度相等的火柴棒可以搭成一个等边三角形（如图1），用5根长度相等的火柴棒可以搭成一个等腰三角形（如图2），用12根长度相等的火柴棒可以搭成几个三角形？它们分别是什么三角形？等腰三角形等边三角形直角三角形课后作业：（1）已知三角形三边长为整数2，x-3，4，则共
可作出不同形状的三角形？当x为多少时，所
作三角形周长最长？(2) 已知三条线段a，b，c，满足下列关系式：
c=2a，b+2a =3c．这三条线段的长能组
成三角形吗？若能，请说明理由；若不能，请
举一个例子说明．
(3) 用16根等长的火柴棒摆成的三角形中，最长边
最多可以由____根火柴棒组成