人教版数学八年级上册 13.3.2.2 含30°角的直角三角形的性质 课件(共12张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.2.2 含30°角的直角三角形的性质 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 00:00:00 | ||
图片预览


文档简介
(共12张PPT)
13.3.2.2 含30°角的直角三角形的性质
1.探索含30°角的直角三角形的性质.
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.
学 习 目 标
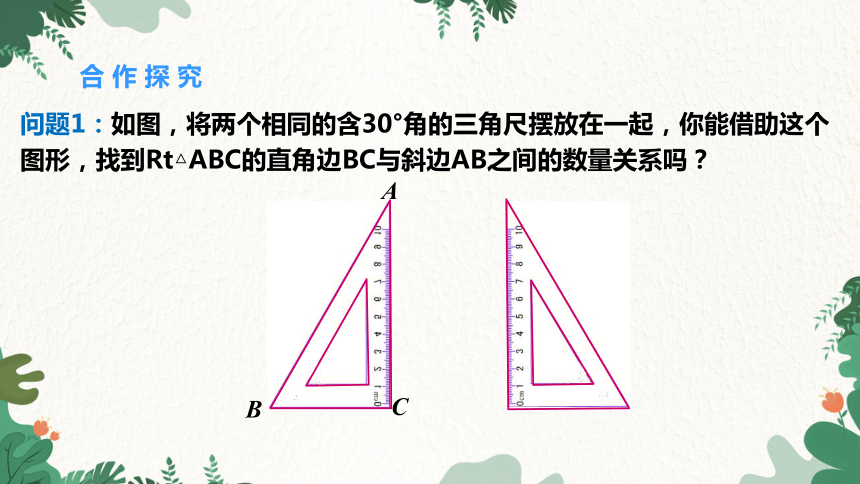
问题1:如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
A
C
B
合 作 探 究
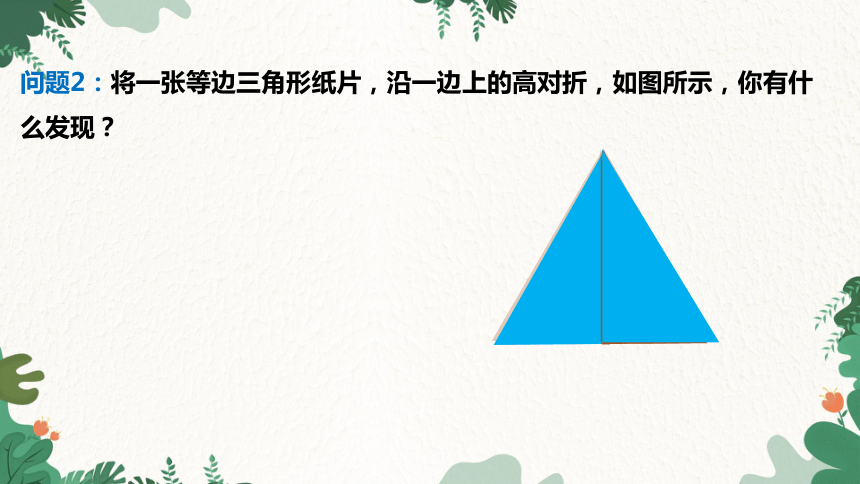
问题2:将一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
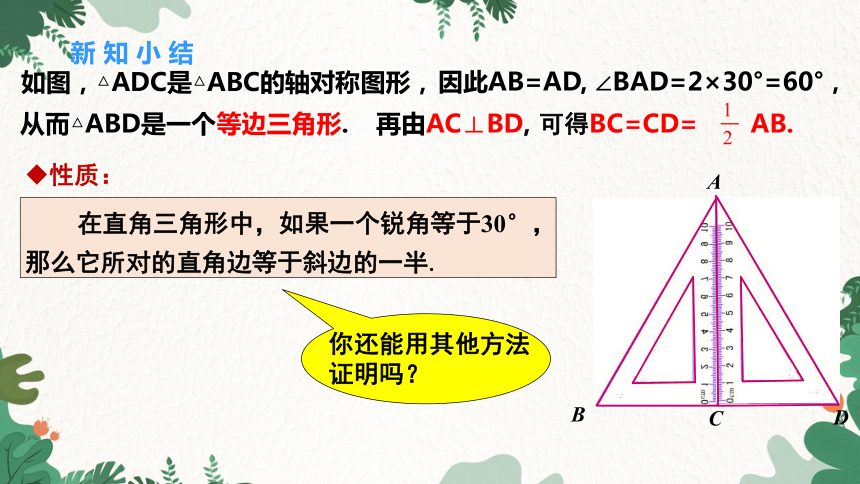
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
新 知 小 结
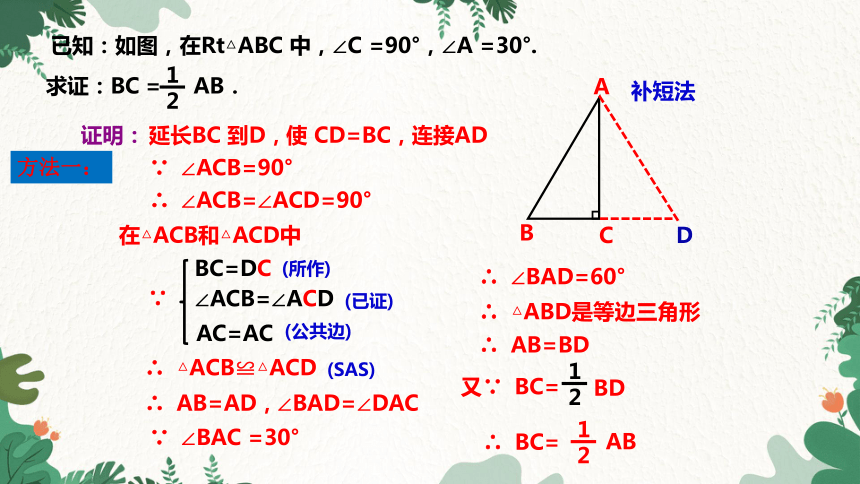
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
A
B
C
D
1
2
求证:BC
证明:
延长BC 到D,
使 CD=BC,
连接AD
在△ACB和△ACD中
AC=AC
∠ACB=∠ACD
BC=DC
∵
(公共边)
(已证)
(所作)
∵ ∠ACB=90°
∴ ∠ACB=∠ACD=90°
∴ △ACB≌△ACD
∴ AB=AD,
∠BAD=∠DAC
∵ ∠BAC =30°
∴ ∠BAD=60°
∴ △ABD是等边三角形
又∵ BC=
∴ AB=BD
1
2
BD
∴ BC=
1
2
AB
(SAS)
补短法
= AB.
方法一:
E
A
B
C
证明: 在BA上截取BE=BC,连接EC.
∵ ∠B= 60° ,BE=BC.
∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC-∠A=60°-30° = 30°.
∴ AE=EC,
∴ AE=BE=BC,
∴ AB=AE+BE=2BC.
∴BC = AB.
证明方法截半法
方法二:
判断下列说法是否正确:
1.直角三角形中30°角所对的直角边等于另一直角边的一半.
2.三角形中30°角所对的边等于最长边的一半。
3.直角三角形中较短的直角边是斜边的一半。
4.直角三角形的斜边是30°角所对直角边的2倍.
√
典 例 精 析
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
2.某市在旧城改造中,计划在一块如图所示的△ABC空地上种植草皮以美化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
B
B
随 堂 练 习
3.在△ABC中,∠C=90°,∠B=15°,DE是AB的垂直平分线,BE=5,则求AC的长.
解:连接AE,
∵DE是AB的垂直平分线,
∴BE=AE,
∴∠EAB=∠B=15°,
∴∠AEC=∠EAB+∠B=30°.
∵∠C=90°,
∴AC= AE= BE=2.5.
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
使用要点
找准30 °的角所对的直角边,点明斜边
注意
前提条件:直角三角形中
含
30°
角
的
直
角
三
角
形
的
性
质
课 堂 总 结
谢谢大家!
13.3.2.2 含30°角的直角三角形的性质
1.探索含30°角的直角三角形的性质.
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.
学 习 目 标
问题1:如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
A
C
B
合 作 探 究
问题2:将一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
新 知 小 结
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
A
B
C
D
1
2
求证:BC
证明:
延长BC 到D,
使 CD=BC,
连接AD
在△ACB和△ACD中
AC=AC
∠ACB=∠ACD
BC=DC
∵
(公共边)
(已证)
(所作)
∵ ∠ACB=90°
∴ ∠ACB=∠ACD=90°
∴ △ACB≌△ACD
∴ AB=AD,
∠BAD=∠DAC
∵ ∠BAC =30°
∴ ∠BAD=60°
∴ △ABD是等边三角形
又∵ BC=
∴ AB=BD
1
2
BD
∴ BC=
1
2
AB
(SAS)
补短法
= AB.
方法一:
E
A
B
C
证明: 在BA上截取BE=BC,连接EC.
∵ ∠B= 60° ,BE=BC.
∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC-∠A=60°-30° = 30°.
∴ AE=EC,
∴ AE=BE=BC,
∴ AB=AE+BE=2BC.
∴BC = AB.
证明方法截半法
方法二:
判断下列说法是否正确:
1.直角三角形中30°角所对的直角边等于另一直角边的一半.
2.三角形中30°角所对的边等于最长边的一半。
3.直角三角形中较短的直角边是斜边的一半。
4.直角三角形的斜边是30°角所对直角边的2倍.
√
典 例 精 析
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
2.某市在旧城改造中,计划在一块如图所示的△ABC空地上种植草皮以美化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
B
B
随 堂 练 习
3.在△ABC中,∠C=90°,∠B=15°,DE是AB的垂直平分线,BE=5,则求AC的长.
解:连接AE,
∵DE是AB的垂直平分线,
∴BE=AE,
∴∠EAB=∠B=15°,
∴∠AEC=∠EAB+∠B=30°.
∵∠C=90°,
∴AC= AE= BE=2.5.
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
使用要点
找准30 °的角所对的直角边,点明斜边
注意
前提条件:直角三角形中
含
30°
角
的
直
角
三
角
形
的
性
质
课 堂 总 结
谢谢大家!
