5.3.1 平行线的性质(1)课时卷
文档属性
| 名称 | 5.3.1 平行线的性质(1)课时卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-14 08:48:58 | ||
图片预览

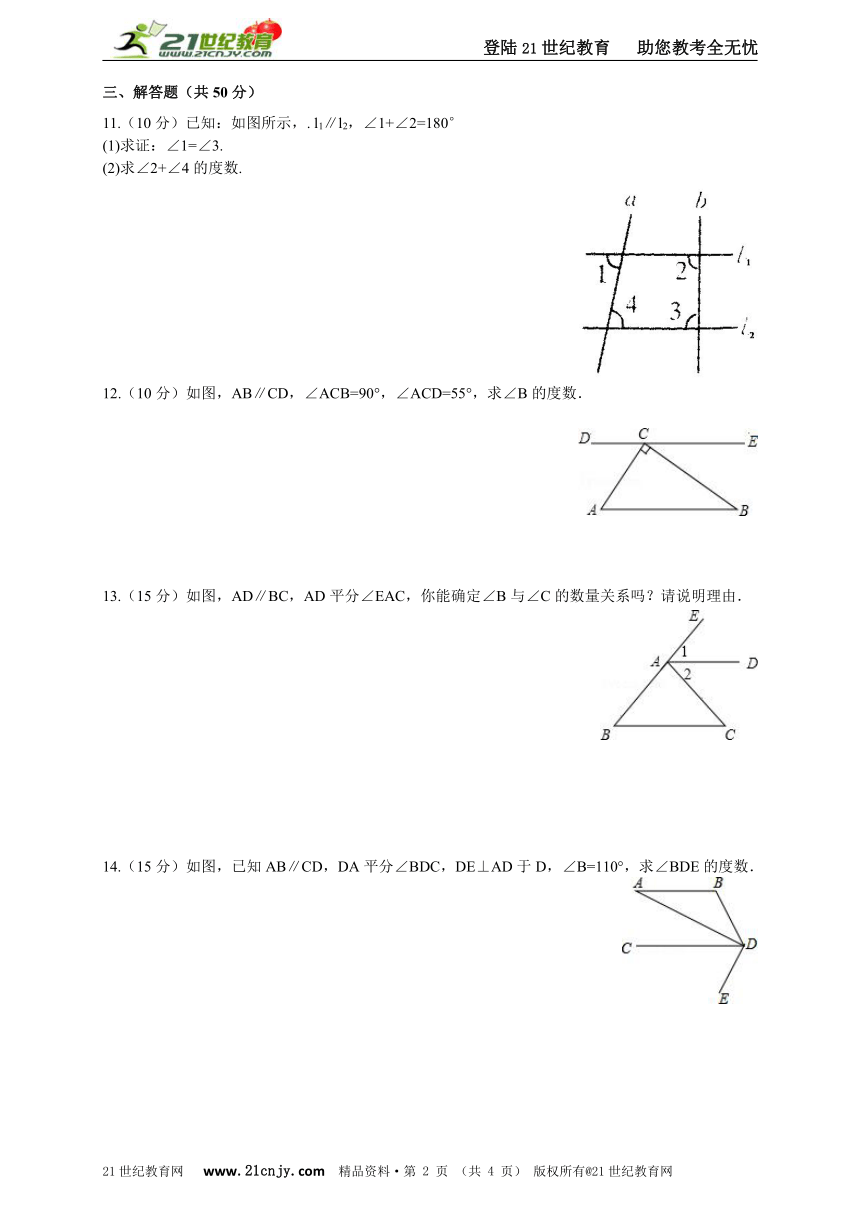
文档简介
八年级数学(下)课时卷
5.3.1 平行线的性质(一)
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.如图,AB//CD,EF分别为交AB,CD于点E,F,∠1=50°,则∠2的度数为( )
A.50° B.120° C.130° D.150°
2.如图,直线a∥b,若∠1=120°,则∠2等于( )
A.60° B.80° C.120° D.150°
第1题图 第2题图 第3题图 第4题图
3.如图,直线l∥OB,则∠1的度数是( )
A. 120° B. 30° C. 40° D. 60°
4.如图,AD平分∠BAC,DE∥AC交AB于点E,∠1=25°,则∠BED等于( )
A.40° B.50° C.60° D.25°
5.下列图形中,由AB//CD能得到∠1=∠2的是( )
二、填空题(每题5分,共25分)
6.如图,AB∥CD,∠CFE=112°,ED平分∠BEF,交CD于D,则∠EDF= .
7.如图,点D,E分别在AB,BC上,DE∥AC,AF∥BC,∠2=70°,则∠1= °.
第6题图 第7题图 第8题图 第9题图 第10题图
8.如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2= .21教育网
9.已知:如图,∠1=∠2=∠3=50°则∠4的度数是 .
10.如图,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,则∠AEC= .
三、解答题(共50分)
11.(10分)已知:如图所示,. l1∥l2,∠1+∠2=180°
(1)求证:∠1=∠3.
(2)求∠2+∠4的度数.
12.(10分)如图,AB∥CD,∠ACB=90°,∠ACD=55°,求∠B的度数.
13.(15分)如图,AD∥BC,AD平分∠EAC,你能确定∠B与∠C的数量关系吗?请说明理由.
14.(15分)如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
参考答案
5.3.1 平行线的性质(一)
2.A
【解析】根据两直线平行,同旁内角与补解答.
3.D
【解析】根据两直线平行,同位角相等解答.
解:∵直线l∥OB,
∴∠1=60°.
故选D.
4.B
【解析】∵DE∥AC交AB于点E,∠1=25°,
∴∠BAC=∠BED,∠1=∠DAC=25°.
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∴∠BED=∠BAC=50°.
故选B.
5.B.
【解析】A、∵AB∥CD,
∴∠1+∠2=180°,
故A选项错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B选项正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C选项错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D选项错误.
故选B.
6.56°.
【解析】∵AB∥CD,∴∠BEF=∠CFE=112°,∵ED平分∠BEF,∴∠BED=112°×=56°,
又∵AB∥CD,∴∠EDF=∠BED=56°.故答案为:56°.
7.70
【解析】解:∵AF∥BC ,∴∠2=∠C=70°,又∵DE∥AC,∴∠1=∠C=70°;故答案为70 .
8.115°
【解析】将各顶点标上 字母,根据平行线的性质可得∠2=∠DEG=∠1+∠FEG,从而可得出答案.
解答: 解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠2=∠DEG=∠1+∠FEG=115°.
故答案为:115°.
9.130°
【解析】根据平行线的判定得出这两条直线平行,根据平行线的性质求出∠4=180°-∠3,求出∠4即可.21世纪教育网版权所有
10.90°
【解析】∵AB∥CD,∴∠BAC+∠ACD=180°,
∵AE、CE分别是∠BAC与∠ACD的平分线,
∴∠EAC+∠ACE=(∠BAC+∠ACD)=×180°=90°,
∴∠AEC=180°-(∠EAC+∠ACE)=180°-90°=90°.
11.【解析】
(1)∵l1∥l2 ∴∠2+∠3=180°(两直线平行,同旁内角互补),∵∠1+∠2=180 °(已知),∴∠1=∠3(同角的补角相等). 21cnjy.com
(2)∵l1∥l2 ∴∠1=∠4(两直线平行,内错角相等),∵∠1+∠2=180°(已知),∴∠2 +∠4=180°(等量代换)21·cn·jy·com
12.【解析】
解:∵AB∥CD,∠ACD=55°,
∴∠A=∠ACD=55°,
∵∠ACB=90°,
∴∠B=180π﹣∠A=90°﹣55°=35°.
13.【解析】解:∠B=∠C.
理由是:∵AD平分∠EAC,
∴∠1=∠2;
∵AD∥BC,
∴∠B=∠1,∠C=∠2;
∴∠B=∠C.
5.3.1 平行线的性质(一)
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.如图,AB//CD,EF分别为交AB,CD于点E,F,∠1=50°,则∠2的度数为( )
A.50° B.120° C.130° D.150°
2.如图,直线a∥b,若∠1=120°,则∠2等于( )
A.60° B.80° C.120° D.150°
第1题图 第2题图 第3题图 第4题图
3.如图,直线l∥OB,则∠1的度数是( )
A. 120° B. 30° C. 40° D. 60°
4.如图,AD平分∠BAC,DE∥AC交AB于点E,∠1=25°,则∠BED等于( )
A.40° B.50° C.60° D.25°
5.下列图形中,由AB//CD能得到∠1=∠2的是( )
二、填空题(每题5分,共25分)
6.如图,AB∥CD,∠CFE=112°,ED平分∠BEF,交CD于D,则∠EDF= .
7.如图,点D,E分别在AB,BC上,DE∥AC,AF∥BC,∠2=70°,则∠1= °.
第6题图 第7题图 第8题图 第9题图 第10题图
8.如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2= .21教育网
9.已知:如图,∠1=∠2=∠3=50°则∠4的度数是 .
10.如图,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,则∠AEC= .
三、解答题(共50分)
11.(10分)已知:如图所示,. l1∥l2,∠1+∠2=180°
(1)求证:∠1=∠3.
(2)求∠2+∠4的度数.
12.(10分)如图,AB∥CD,∠ACB=90°,∠ACD=55°,求∠B的度数.
13.(15分)如图,AD∥BC,AD平分∠EAC,你能确定∠B与∠C的数量关系吗?请说明理由.
14.(15分)如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
参考答案
5.3.1 平行线的性质(一)
2.A
【解析】根据两直线平行,同旁内角与补解答.
3.D
【解析】根据两直线平行,同位角相等解答.
解:∵直线l∥OB,
∴∠1=60°.
故选D.
4.B
【解析】∵DE∥AC交AB于点E,∠1=25°,
∴∠BAC=∠BED,∠1=∠DAC=25°.
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∴∠BED=∠BAC=50°.
故选B.
5.B.
【解析】A、∵AB∥CD,
∴∠1+∠2=180°,
故A选项错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B选项正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C选项错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D选项错误.
故选B.
6.56°.
【解析】∵AB∥CD,∴∠BEF=∠CFE=112°,∵ED平分∠BEF,∴∠BED=112°×=56°,
又∵AB∥CD,∴∠EDF=∠BED=56°.故答案为:56°.
7.70
【解析】解:∵AF∥BC ,∴∠2=∠C=70°,又∵DE∥AC,∴∠1=∠C=70°;故答案为70 .
8.115°
【解析】将各顶点标上 字母,根据平行线的性质可得∠2=∠DEG=∠1+∠FEG,从而可得出答案.
解答: 解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠2=∠DEG=∠1+∠FEG=115°.
故答案为:115°.
9.130°
【解析】根据平行线的判定得出这两条直线平行,根据平行线的性质求出∠4=180°-∠3,求出∠4即可.21世纪教育网版权所有
10.90°
【解析】∵AB∥CD,∴∠BAC+∠ACD=180°,
∵AE、CE分别是∠BAC与∠ACD的平分线,
∴∠EAC+∠ACE=(∠BAC+∠ACD)=×180°=90°,
∴∠AEC=180°-(∠EAC+∠ACE)=180°-90°=90°.
11.【解析】
(1)∵l1∥l2 ∴∠2+∠3=180°(两直线平行,同旁内角互补),∵∠1+∠2=180 °(已知),∴∠1=∠3(同角的补角相等). 21cnjy.com
(2)∵l1∥l2 ∴∠1=∠4(两直线平行,内错角相等),∵∠1+∠2=180°(已知),∴∠2 +∠4=180°(等量代换)21·cn·jy·com
12.【解析】
解:∵AB∥CD,∠ACD=55°,
∴∠A=∠ACD=55°,
∵∠ACB=90°,
∴∠B=180π﹣∠A=90°﹣55°=35°.
13.【解析】解:∠B=∠C.
理由是:∵AD平分∠EAC,
∴∠1=∠2;
∵AD∥BC,
∴∠B=∠1,∠C=∠2;
∴∠B=∠C.
