第二十二章 二次函数单元检测试题(含答案)
文档属性
| 名称 | 第二十二章 二次函数单元检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-28 16:13:56 | ||
图片预览



文档简介
第二十二章《二次函数》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.抛物线与轴交点的坐标是
A. B. C. D.
2.抛物线的对称轴是
A.直线 B.直线 C.直线 D.直线
3.对于二次函数,下列说法正确的是
A.当时,随的增大而增大
B.当时,有最大值
C.图象的顶点坐标为
D.图象与轴有两个交点
A.-3 B.-1 C.2 D.3
4.将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
A.y=(x+1)2-13 B.y=(x-5)2-3
C.y=(x-5)2-13 D.y=(x+1)2-3
5.将抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )
A.y=(x﹣1)2+4 B.y=(x﹣4)2+4
C.y=(x+2)2+6 D.y=(x﹣4)2+6
6.已知二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,则k的取值范围为( )
A.k>﹣1 B.k>﹣1且k≠0
C.k≥﹣1 D.k≥﹣1且k≠0
7.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A.B. C.D.
8. 如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A.-1≤x≤3 B.x≤-1 C.x≥1 D.x≤-1或x≥3
9.向上发射一枚炮弹,经秒后的高度为公尺,且时间(秒与高度(公尺)的关系为.、为常数,且若此炮弹在第6秒与第11秒时的高度相等,则下列哪一个时间的高度是最高的?
A.第7秒 B.第8秒 C.第10秒 D.第12秒
10.二次函数的图象如图所示.下列结论:①;②;③为任意实数,则;④;⑤若且,则.其中正确结论的个数有
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.已知函数是二次函数,则m=________.
12.已知二次函数,当时,,则这个二次函数的表达式是________。
13.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加______m。
14.抛物线y=x2﹣k的顶点为P,与x轴交于A、B两点,如果△ABP是正三角形,那么k= .
15.把y=2x2﹣6x+4配方成y=a(x﹣h)2+k的形式是 .
16.如图,这是二次函数y=x2﹣2x﹣3的图象,根据图象可知,函数值小于0时x的取值范围为 .
17.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为 .
18.如图,用长为10米的篱笆,一面靠墙(墙的长度超过10米),围成一个矩形花圃,设矩形垂直于墙的一边长为x米,花圃面积为S平方米,则S关于x的函数解析式是______(不写定义域).
三.解答题(共46分,19题6分,20 ---24题8分)
19.二次函数的图象经过点A(1,4)和B(0,1)求二次函数的表达式和该抛物线的顶点坐标、对称轴.
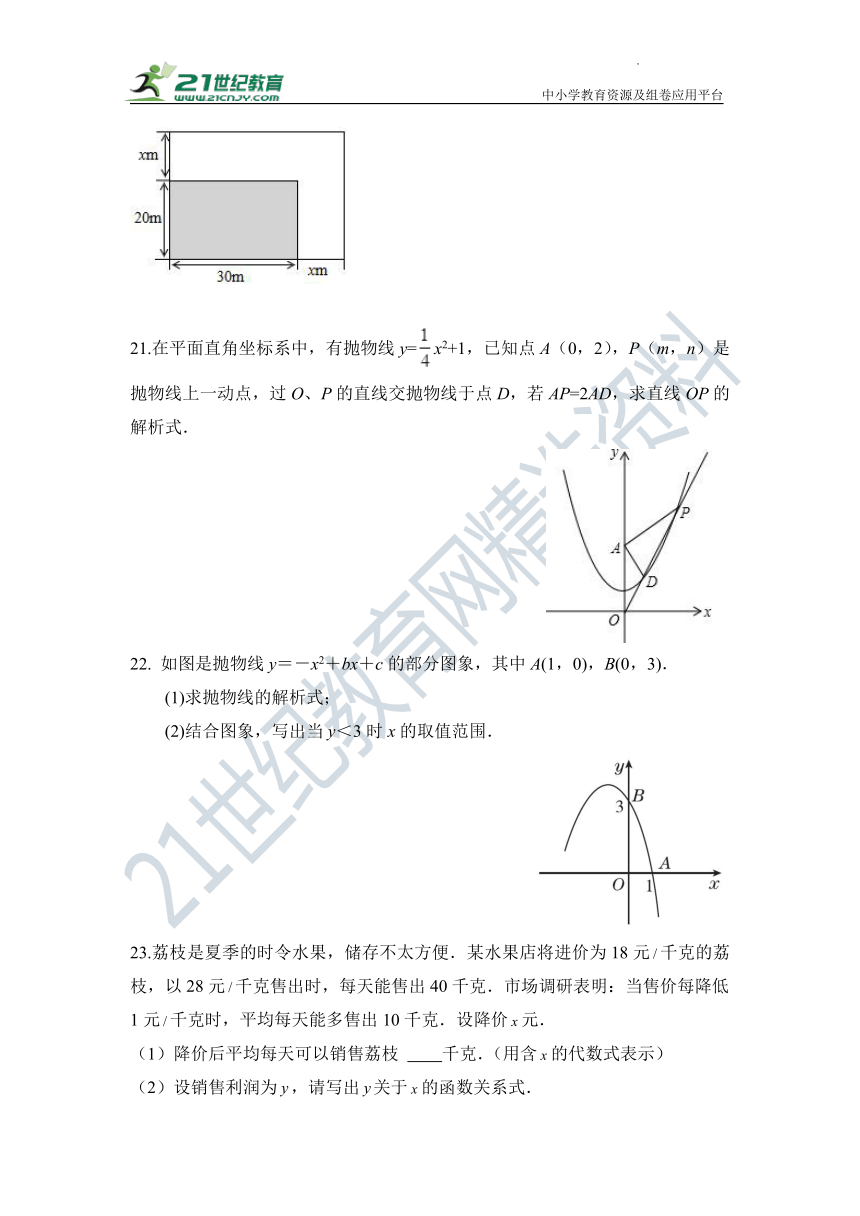
20.如图,矩形绿地的长、宽各增加,写出扩充后的绿地的面积y与x的关系式.
21.在平面直角坐标系中,有抛物线y=x2+1,已知点A(0,2),P(m,n)是抛物线上一动点,过O、P的直线交抛物线于点D,若AP=2AD,求直线OP的解析式.
22. 如图是抛物线y=-x2+bx+c的部分图象,其中A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合图象,写出当y<3时x的取值范围.
23.荔枝是夏季的时令水果,储存不太方便.某水果店将进价为18元千克的荔枝,以28元千克售出时,每天能售出40千克.市场调研表明:当售价每降低1元千克时,平均每天能多售出10千克.设降价元.
(1)降价后平均每天可以销售荔枝 千克.(用含的代数式表示)
(2)设销售利润为,请写出关于的函数关系式.
(3)该水果店想要使荔枝的销售利润平均每天达到480元,且尽可能地减少库存压力,应将价格定为多少元千克?
24.如图,直线交轴于点,交轴于点,抛物线经过点,,顶点为点.
(1)求抛物线的解析式及点的坐标.
(2)将抛物线向下平移个单位长度,点的对应点为,连结,,若,求的值.
答案解析
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D B C C C B B
二、填空题
11.
12.
13.
14.
【分析】根据抛物线y=x2﹣k的顶点为P,可直接求出P点的坐标,进而得出OP的长度,又因为△ABP是正三角形,得出∠OPB=30°,利用锐角三角函数即可求出OB的长度,得出B点的坐标,代入二次函数解析式即可求出k的值.
【解答】解:∵抛物线y=x2﹣k的顶点为P,
∴P点的坐标为:(0,﹣k),∴PO=K,
∵抛物线y=x2﹣k与x轴交于A、B两点,且△ABP是正三角形,
∴OA=OB,∠OPB=30°,
∴tan30°==,
∴OB=k,
∴点B的坐标为:(k,0),点B在抛物线y=x2﹣k上,
∴将B点代入y=x2﹣k,得:
0=(k)2﹣k,
整理得:﹣k=0,
解方程得:k1=0(不合题意舍去),k2=3.
故答案为:3.
【点评】此题主要考查了二次函数顶点坐标的求法,以及正三角形的性质和锐角三角函数求值问题等知识,求出A或B点的坐标进而代入二次函数解析式是解决问题的关键.
15.解:y=2x2﹣6x+4=2(x2﹣3x+)﹣2×+4=2(x﹣)2﹣.
即y=2(x﹣)2﹣.
故答案为y=2(x﹣)2﹣.
16.如图,这是二次函数y=x2﹣2x﹣3的图象,根据图象可知,函数值小于0时x的取值范围为 ﹣1<x<3 .
【分析】根据函数图象和二次函数的性质可以直接写出函数值小于0时x的取值范围.
【解答】解:由图象可知,
抛物线与x轴的两个交点时(﹣1,0),(3,0),抛物线开口向上,
∴函数值小于0时x的取值范围为﹣1<x<3,
故答案为:﹣1<x<3.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.
17.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为 y=(60﹣x)(300+20x) .
【分析】根据题意可以列出相应的函数关系式,本题得以解决.
【解答】解:由题意可得,
y=(60﹣x)(300+20x),
故答案为:y=(60﹣x)(300+20x).
【点评】本题考查由实际问题列二次函数关系式,解答本题的关键是明确题意,列出相应的函数关系式.
18.
三.解答题
19.,顶点坐标为(0,1)、对称轴为直线x=0.
【解析】解:∵二次函数的图象经过点A(1,4)和B(0,1),
∴,
∴,
∴,
∴该抛物线的顶点坐标为(0,1)、对称轴为直线x=0.
20.
【解析】解:∵矩形原来的长和宽分别为30m、20m,矩形绿地的长、宽各增加xm,
∴增加后的矩形的长和宽分别为(20+x)m,(30+x)m,
∴.
21.【答案】解:∵P(m,n)是抛物线y=x2+1上一动点,∴m2+1=n,∴m2=4n-4,∵点A(0,2),∴AP===n,∴点P到点A的距离等于点P的纵坐标,过点D作DE⊥x轴于E,过点P作PF⊥x轴于F,∵AP=2AD,∴PF=2DE,∴OF=2OE,设OE=a,则OF=2a,∴×(2a)2+1=2(a2+1),解得a=,∴a2+1=×2+1=,∴点D的坐标为(,),设OP的解析式为y=kx,则k=,解得k=,∴直线OP的解析式为y=x.
【解析】根据点P在抛物线上用n表示出m2,再利用勾股定理列式求出AP,从而得到点P到点A的距离等于点P的纵坐标,过点D作DE⊥x轴于E,过点P作PF⊥x轴于F,根据AP=2AD判断出PF=2DE,得到OF=2OE,设OE=a,表示出OF=2a,然后代入抛物线解析式并列出方程求出a的值,再求出点D的坐标,最后利用待定系数法求一次函数解析式解答.
23.【解析】解:(1)根据题意可知降后平均每天可以销售荔枝:千克,
故答案为:.
(2)根据题意可知,,
整理得.
(3)令,代入函数得,
解方程,得,,
要尽可能地清空库存,
,
此时荔枝定价为(元千克).
答:应将价格定为24元千克.
24.【解析】解:(1)直线交轴于点,交轴于点,
点,点,
抛物线经过点,,
,
解得,
抛物线的解析式为:,
,
;
(2)将抛物线向下平移个单位长度得到,
把代入得,
与对称轴的交点为,
平移后的抛物线的顶点为,
,
,
或.
的值为或.
中小学教育资源及组卷应用平台
(北京)股份有限公司
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.抛物线与轴交点的坐标是
A. B. C. D.
2.抛物线的对称轴是
A.直线 B.直线 C.直线 D.直线
3.对于二次函数,下列说法正确的是
A.当时,随的增大而增大
B.当时,有最大值
C.图象的顶点坐标为
D.图象与轴有两个交点
A.-3 B.-1 C.2 D.3
4.将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
A.y=(x+1)2-13 B.y=(x-5)2-3
C.y=(x-5)2-13 D.y=(x+1)2-3
5.将抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )
A.y=(x﹣1)2+4 B.y=(x﹣4)2+4
C.y=(x+2)2+6 D.y=(x﹣4)2+6
6.已知二次函数y=kx2﹣6x﹣9的图象与x轴有两个不同的交点,则k的取值范围为( )
A.k>﹣1 B.k>﹣1且k≠0
C.k≥﹣1 D.k≥﹣1且k≠0
7.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A.B. C.D.
8. 如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是( )
A.-1≤x≤3 B.x≤-1 C.x≥1 D.x≤-1或x≥3
9.向上发射一枚炮弹,经秒后的高度为公尺,且时间(秒与高度(公尺)的关系为.、为常数,且若此炮弹在第6秒与第11秒时的高度相等,则下列哪一个时间的高度是最高的?
A.第7秒 B.第8秒 C.第10秒 D.第12秒
10.二次函数的图象如图所示.下列结论:①;②;③为任意实数,则;④;⑤若且,则.其中正确结论的个数有
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.已知函数是二次函数,则m=________.
12.已知二次函数,当时,,则这个二次函数的表达式是________。
13.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加______m。
14.抛物线y=x2﹣k的顶点为P,与x轴交于A、B两点,如果△ABP是正三角形,那么k= .
15.把y=2x2﹣6x+4配方成y=a(x﹣h)2+k的形式是 .
16.如图,这是二次函数y=x2﹣2x﹣3的图象,根据图象可知,函数值小于0时x的取值范围为 .
17.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为 .
18.如图,用长为10米的篱笆,一面靠墙(墙的长度超过10米),围成一个矩形花圃,设矩形垂直于墙的一边长为x米,花圃面积为S平方米,则S关于x的函数解析式是______(不写定义域).
三.解答题(共46分,19题6分,20 ---24题8分)
19.二次函数的图象经过点A(1,4)和B(0,1)求二次函数的表达式和该抛物线的顶点坐标、对称轴.
20.如图,矩形绿地的长、宽各增加,写出扩充后的绿地的面积y与x的关系式.
21.在平面直角坐标系中,有抛物线y=x2+1,已知点A(0,2),P(m,n)是抛物线上一动点,过O、P的直线交抛物线于点D,若AP=2AD,求直线OP的解析式.
22. 如图是抛物线y=-x2+bx+c的部分图象,其中A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合图象,写出当y<3时x的取值范围.
23.荔枝是夏季的时令水果,储存不太方便.某水果店将进价为18元千克的荔枝,以28元千克售出时,每天能售出40千克.市场调研表明:当售价每降低1元千克时,平均每天能多售出10千克.设降价元.
(1)降价后平均每天可以销售荔枝 千克.(用含的代数式表示)
(2)设销售利润为,请写出关于的函数关系式.
(3)该水果店想要使荔枝的销售利润平均每天达到480元,且尽可能地减少库存压力,应将价格定为多少元千克?
24.如图,直线交轴于点,交轴于点,抛物线经过点,,顶点为点.
(1)求抛物线的解析式及点的坐标.
(2)将抛物线向下平移个单位长度,点的对应点为,连结,,若,求的值.
答案解析
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D B C C C B B
二、填空题
11.
12.
13.
14.
【分析】根据抛物线y=x2﹣k的顶点为P,可直接求出P点的坐标,进而得出OP的长度,又因为△ABP是正三角形,得出∠OPB=30°,利用锐角三角函数即可求出OB的长度,得出B点的坐标,代入二次函数解析式即可求出k的值.
【解答】解:∵抛物线y=x2﹣k的顶点为P,
∴P点的坐标为:(0,﹣k),∴PO=K,
∵抛物线y=x2﹣k与x轴交于A、B两点,且△ABP是正三角形,
∴OA=OB,∠OPB=30°,
∴tan30°==,
∴OB=k,
∴点B的坐标为:(k,0),点B在抛物线y=x2﹣k上,
∴将B点代入y=x2﹣k,得:
0=(k)2﹣k,
整理得:﹣k=0,
解方程得:k1=0(不合题意舍去),k2=3.
故答案为:3.
【点评】此题主要考查了二次函数顶点坐标的求法,以及正三角形的性质和锐角三角函数求值问题等知识,求出A或B点的坐标进而代入二次函数解析式是解决问题的关键.
15.解:y=2x2﹣6x+4=2(x2﹣3x+)﹣2×+4=2(x﹣)2﹣.
即y=2(x﹣)2﹣.
故答案为y=2(x﹣)2﹣.
16.如图,这是二次函数y=x2﹣2x﹣3的图象,根据图象可知,函数值小于0时x的取值范围为 ﹣1<x<3 .
【分析】根据函数图象和二次函数的性质可以直接写出函数值小于0时x的取值范围.
【解答】解:由图象可知,
抛物线与x轴的两个交点时(﹣1,0),(3,0),抛物线开口向上,
∴函数值小于0时x的取值范围为﹣1<x<3,
故答案为:﹣1<x<3.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.
17.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为 y=(60﹣x)(300+20x) .
【分析】根据题意可以列出相应的函数关系式,本题得以解决.
【解答】解:由题意可得,
y=(60﹣x)(300+20x),
故答案为:y=(60﹣x)(300+20x).
【点评】本题考查由实际问题列二次函数关系式,解答本题的关键是明确题意,列出相应的函数关系式.
18.
三.解答题
19.,顶点坐标为(0,1)、对称轴为直线x=0.
【解析】解:∵二次函数的图象经过点A(1,4)和B(0,1),
∴,
∴,
∴,
∴该抛物线的顶点坐标为(0,1)、对称轴为直线x=0.
20.
【解析】解:∵矩形原来的长和宽分别为30m、20m,矩形绿地的长、宽各增加xm,
∴增加后的矩形的长和宽分别为(20+x)m,(30+x)m,
∴.
21.【答案】解:∵P(m,n)是抛物线y=x2+1上一动点,∴m2+1=n,∴m2=4n-4,∵点A(0,2),∴AP===n,∴点P到点A的距离等于点P的纵坐标,过点D作DE⊥x轴于E,过点P作PF⊥x轴于F,∵AP=2AD,∴PF=2DE,∴OF=2OE,设OE=a,则OF=2a,∴×(2a)2+1=2(a2+1),解得a=,∴a2+1=×2+1=,∴点D的坐标为(,),设OP的解析式为y=kx,则k=,解得k=,∴直线OP的解析式为y=x.
【解析】根据点P在抛物线上用n表示出m2,再利用勾股定理列式求出AP,从而得到点P到点A的距离等于点P的纵坐标,过点D作DE⊥x轴于E,过点P作PF⊥x轴于F,根据AP=2AD判断出PF=2DE,得到OF=2OE,设OE=a,表示出OF=2a,然后代入抛物线解析式并列出方程求出a的值,再求出点D的坐标,最后利用待定系数法求一次函数解析式解答.
23.【解析】解:(1)根据题意可知降后平均每天可以销售荔枝:千克,
故答案为:.
(2)根据题意可知,,
整理得.
(3)令,代入函数得,
解方程,得,,
要尽可能地清空库存,
,
此时荔枝定价为(元千克).
答:应将价格定为24元千克.
24.【解析】解:(1)直线交轴于点,交轴于点,
点,点,
抛物线经过点,,
,
解得,
抛物线的解析式为:,
,
;
(2)将抛物线向下平移个单位长度得到,
把代入得,
与对称轴的交点为,
平移后的抛物线的顶点为,
,
,
或.
的值为或.
中小学教育资源及组卷应用平台
(北京)股份有限公司
同课章节目录
