初中数学北师大版八年级上作业 7.3平行线的判定(含答案)
文档属性
| 名称 | 初中数学北师大版八年级上作业 7.3平行线的判定(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 111.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 19:09:49 | ||
图片预览


文档简介
7.3平行线的判定
一、单选题
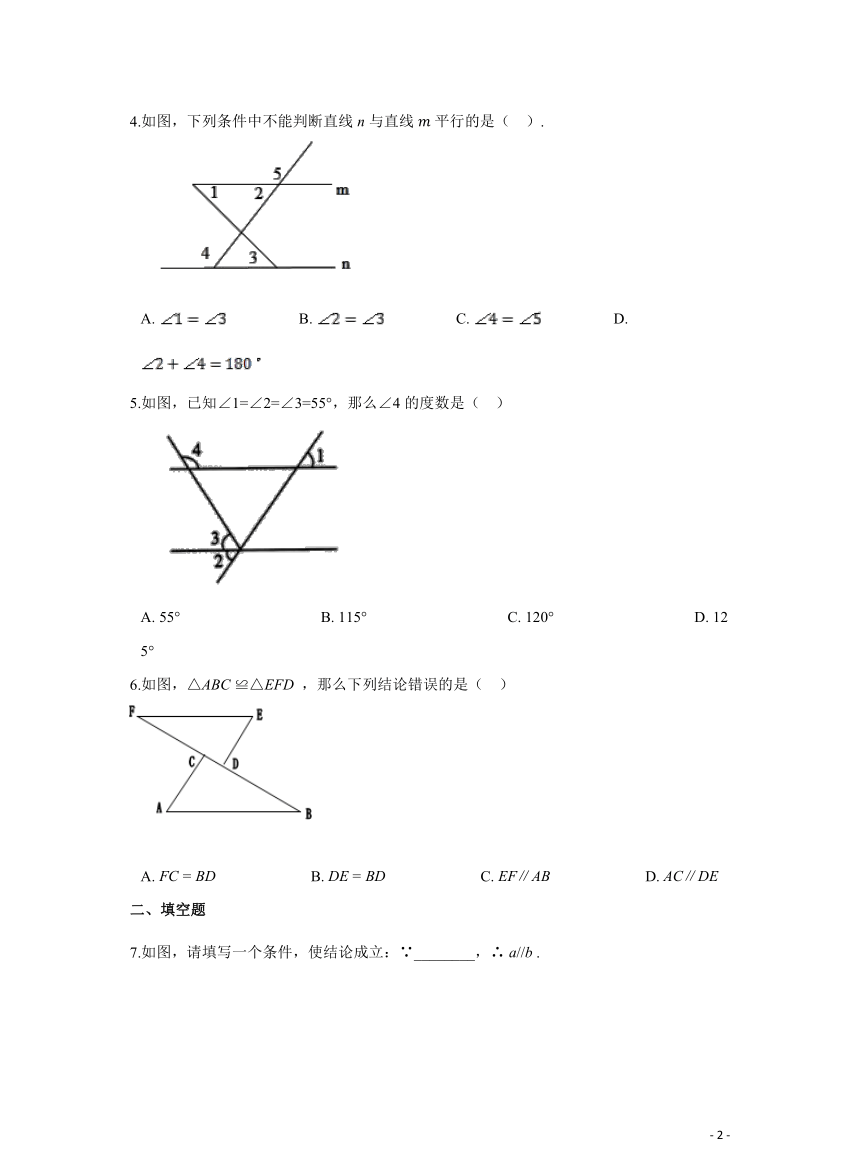
1.如图,直线 被直线 所截下列条件能判定 的是( )
A. B. C. D.
2.如图,已知 ,则图中互相平行的线段是( )
A. AB//CD B. AD//BC C. AB//CD或AD//BC D. AB//CD且AD//BC
3.下图给出了过直线外一点作已知直线的平行线的一种方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 平行于同一直线的两条直线平行
4.如图,下列条件中不能判断直线与直线平行的是( ).
A. B. C. D.
5.如图,已知∠1=∠2=∠3=55°,那么∠4的度数是( )
A. 55° B. 115° C. 120° D. 125°
6.如图,△ ≌△ ,那么下列结论错误的是( )
A. B. C. ∥ D. ∥
二、填空题
7.如图,请填写一个条件,使结论成立:∵________,∴ .
8.如图,将两个含角 30°的直角三角板的最长边靠在一起滑动,可知直角边 ,依据是________.
三、综合题
9.完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴∠ADC+∠C=180°.
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1= ∠ABC.
同理,∠2= ∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
10.如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
(1)求证:ED∥BC;
(2)若D,E,F分别是AB,AC,CD边上的中点,四边形ADFE的面积为6.求△ABC的面积;
(3)若G是BC边上一点,CG=2BG,求△FCG的面积.
11.如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
答案解析部分
一、单选题
1.【答案】 D
2.【答案】 B
3.【答案】 A
4.【答案】 B
5.【答案】 D
6.【答案】 B
二、填空题
7.【答案】 ∠1=∠4(答案不唯一)
8.【答案】 内错角相等,两直线平行
三、综合题
9.【答案】 证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.(两直线平行,同旁内角相等)
又∵AD∥BC,(已知)
∴∠ADC+∠C=180°.
∴∠ABC=∠ADC.(等量代换)
∵BE平分∠ABC,(已知)
∴∠1= ∠ABC.
同理,∠2= ∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.(两直线平行,内错角相等)
∴∠1=∠3,
∴BE∥DF.(同位角相等,两直线平行)
10.【答案】 (1)证明:如图,
∵∠BDC+∠EFC=180°,∠EFD+∠EFC=180°,
∴∠BDC=∠EFD,
∴AB∥EF,
∴∠ADE=∠DEF,
又∵∠B=∠DEF,
∴∠B=∠ADE,
∴ED∥BC
(2)解:设△CEF的面积为a,
∵F是CD的中点,
∴S△DEF=a,
∴S△CDE=2a,
同理,S△ADC=4a,S△ABC=8a,
∴S四边形ADFE=3a,
∵四边形ADFE的面积为6.
∴3a=6,即a=2,
∴S△ABC=8a=16;
(3)解:如图,连接DG,
∵CG=2BG,
∴S△DCG=2S△DBG ,
∴ ,
∵F是CD的中点,
∴ .
11.【答案】 (1)解:BF∥CD,理由如下:
因为∠B=42°,∠1=∠2+10°,且三角形内角和为180°
所以∠2=64°
又因为∠ACD=64°,所以∠ACD=∠2,因此BF∥CD;
(2)解:因为CE平分∠ACD,所以∠DCE= ∠ACD=32°
因为BF∥CD,所以∠3=180°- 32°=148°.
- 1 -
一、单选题
1.如图,直线 被直线 所截下列条件能判定 的是( )
A. B. C. D.
2.如图,已知 ,则图中互相平行的线段是( )
A. AB//CD B. AD//BC C. AB//CD或AD//BC D. AB//CD且AD//BC
3.下图给出了过直线外一点作已知直线的平行线的一种方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 平行于同一直线的两条直线平行
4.如图,下列条件中不能判断直线与直线平行的是( ).
A. B. C. D.
5.如图,已知∠1=∠2=∠3=55°,那么∠4的度数是( )
A. 55° B. 115° C. 120° D. 125°
6.如图,△ ≌△ ,那么下列结论错误的是( )
A. B. C. ∥ D. ∥
二、填空题
7.如图,请填写一个条件,使结论成立:∵________,∴ .
8.如图,将两个含角 30°的直角三角板的最长边靠在一起滑动,可知直角边 ,依据是________.
三、综合题
9.完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴∠ADC+∠C=180°.
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1= ∠ABC.
同理,∠2= ∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
10.如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.
(1)求证:ED∥BC;
(2)若D,E,F分别是AB,AC,CD边上的中点,四边形ADFE的面积为6.求△ABC的面积;
(3)若G是BC边上一点,CG=2BG,求△FCG的面积.
11.如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
答案解析部分
一、单选题
1.【答案】 D
2.【答案】 B
3.【答案】 A
4.【答案】 B
5.【答案】 D
6.【答案】 B
二、填空题
7.【答案】 ∠1=∠4(答案不唯一)
8.【答案】 内错角相等,两直线平行
三、综合题
9.【答案】 证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.(两直线平行,同旁内角相等)
又∵AD∥BC,(已知)
∴∠ADC+∠C=180°.
∴∠ABC=∠ADC.(等量代换)
∵BE平分∠ABC,(已知)
∴∠1= ∠ABC.
同理,∠2= ∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.(两直线平行,内错角相等)
∴∠1=∠3,
∴BE∥DF.(同位角相等,两直线平行)
10.【答案】 (1)证明:如图,
∵∠BDC+∠EFC=180°,∠EFD+∠EFC=180°,
∴∠BDC=∠EFD,
∴AB∥EF,
∴∠ADE=∠DEF,
又∵∠B=∠DEF,
∴∠B=∠ADE,
∴ED∥BC
(2)解:设△CEF的面积为a,
∵F是CD的中点,
∴S△DEF=a,
∴S△CDE=2a,
同理,S△ADC=4a,S△ABC=8a,
∴S四边形ADFE=3a,
∵四边形ADFE的面积为6.
∴3a=6,即a=2,
∴S△ABC=8a=16;
(3)解:如图,连接DG,
∵CG=2BG,
∴S△DCG=2S△DBG ,
∴ ,
∵F是CD的中点,
∴ .
11.【答案】 (1)解:BF∥CD,理由如下:
因为∠B=42°,∠1=∠2+10°,且三角形内角和为180°
所以∠2=64°
又因为∠ACD=64°,所以∠ACD=∠2,因此BF∥CD;
(2)解:因为CE平分∠ACD,所以∠DCE= ∠ACD=32°
因为BF∥CD,所以∠3=180°- 32°=148°.
- 1 -
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
