27.2.3相似三角形应用举例课件
文档属性
| 名称 | 27.2.3相似三角形应用举例课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-14 11:57:23 | ||
图片预览








文档简介
课件25张PPT。WXQ乐山大佛WXQ世界上最高的树
—— 红杉WXQ世界上最高的楼
——台北101大楼怎样测量这些非常高大物体的高度?WXQ世界上最宽的河
——亚马孙河怎样测量河宽?WXQ27.2.2 相似三角形应用举例保安初级中学WXQ1、判断两三角形相似有哪些方法?2、相似三角形有什么性质?复习回顾定义,平行法,(SSS),(SAS),(AA),(HL)(1)对应边的比相等,对应角相等
(2)相似三角形的周长比等于相似比
(3)相似三角形的面积比等于相似比的平方
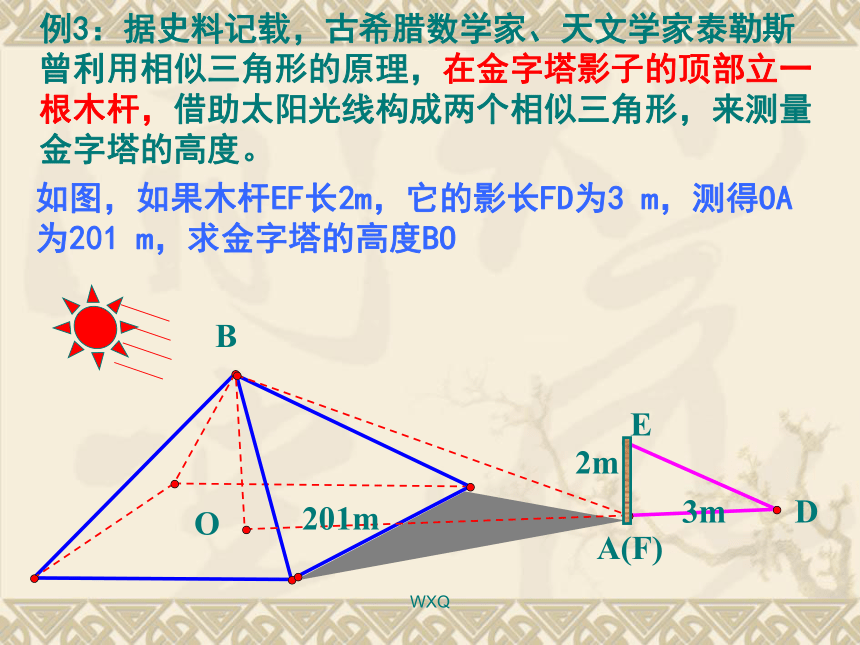
(4)相似三角形的对应边上的高、中线、角 平分线的长度比等于相似比WXQ胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 埃及著名的考古专家穆罕穆德应用举例1WXQ埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅15岁的小穆罕穆德.WXQ例3:据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度。如图,如果木杆EF长2m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO DEA(F)BO2m3m201mWXQDEA(F)BO2m3m201m解:太阳光是平行线, 因此∠BAO= ∠EDF又 ∠AOB= ∠DFE=90°
∴△ABO∽△DEF=BO == 134WXQAFEBO┐┐还可以有其他方法测量吗?=△ABO∽△AEFOB =平面镜一题多解WXQ1、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则答:楼高36米.应用感悟1WXQ如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ADCEB应用举例2WXQ解: 因为 ∠ADB=∠EDC, ?
∠ABC=∠ECD=90°, ? 所以 △ABD∽△ECD, ?
答: 两岸间的大致距离为100米. ?应用举例2WXQ 我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。此时如果测得BD=45米,
DE=90米,BC=60米,
求两岸间的大致距离AB.一题多解WXQ1、如图,测得BD=120m,DC=60m,EC=50m,求河宽AB。解:∵∠B=∠C=90°,
∠ADB=∠EDC,
∴△ABD∽△ECD,
∴ AB:EC=BD:DC
∴ AB=50×120÷60
=100(m)
ABDCE应用感悟2WXQ2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=35m,DC=35m,DE=30m,那么你能算出池塘的宽AB吗?应用感悟2WXQ1. 相似三角形的应用主要有两个方面:(1) 测高 测量不能到达两点间的距离,常构造相似三角形求解。(不能直接使用皮尺或刻度尺量的)(不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。(2) 测距课堂小结2. 解相似三角形实际问题的一般步骤:审题 构建图形 利用相似解决问题WXQ1.小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为 米.WXQ2.数学兴趣小组测校内一棵树高,如图,把镜子放在离树(AB)8M点E处,然后沿着直线BE后退到D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2M,观察者目高CD=1.6M。树高多少米?WXQ3、如图,已知零件的外径a为25cm ,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=3,且量得CD=7cm,求厚度x。O(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。)WXQ4、 已知左、右并排的两棵大树的高分别是
AB=8m和CD=12m,两树的根部的距离
BD=5m,一个身高1.6m的人沿着正
对这两棵树的一条水平直路l从左
向右前进,当他与左边较低的树的距离小于多少时,
就不能看到右边较高的树的顶端点C?
设观察者眼晴的位置(视点)
为F,∠CFK和∠AFH分别是
观察点C、A的仰角,区域Ⅰ
和区域Ⅱ都在观察者看不到
的区域(盲区)之内。WXQ解:假设观察者从左向右走到点E时,他的眼睛的
位置点F与两棵树的顶端点A、C在一条直线上。
∵AB⊥l,CD⊥l,
∴AB∥CD,△AFH∽△CFK,
∴FH:FK=AH:CK,
即
,
解得FH=8.当他与左边较低的树的距离小
于8m时,就不能看到右边较高
的树的顶端点C。
WXQ5.教学楼旁边有一棵树,数学兴趣小组的同学们想利用树影测量树高。课外活动时在阳光下他们测得一根长为1米的竹竿的影长是0.9米,但当他们马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上。他们测得落在地面的影长2.7米,落在墙壁上的影长1.2米,请你和他们一起算一下,树高多少米?图11WXQ6、如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4.5m,如果小明得身高为1.5m,求路灯杆AB的高度。A
—— 红杉WXQ世界上最高的楼
——台北101大楼怎样测量这些非常高大物体的高度?WXQ世界上最宽的河
——亚马孙河怎样测量河宽?WXQ27.2.2 相似三角形应用举例保安初级中学WXQ1、判断两三角形相似有哪些方法?2、相似三角形有什么性质?复习回顾定义,平行法,(SSS),(SAS),(AA),(HL)(1)对应边的比相等,对应角相等
(2)相似三角形的周长比等于相似比
(3)相似三角形的面积比等于相似比的平方
(4)相似三角形的对应边上的高、中线、角 平分线的长度比等于相似比WXQ胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 埃及著名的考古专家穆罕穆德应用举例1WXQ埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅15岁的小穆罕穆德.WXQ例3:据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度。如图,如果木杆EF长2m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO DEA(F)BO2m3m201mWXQDEA(F)BO2m3m201m解:太阳光是平行线, 因此∠BAO= ∠EDF又 ∠AOB= ∠DFE=90°
∴△ABO∽△DEF=BO == 134WXQAFEBO┐┐还可以有其他方法测量吗?=△ABO∽△AEFOB =平面镜一题多解WXQ1、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则答:楼高36米.应用感悟1WXQ如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ADCEB应用举例2WXQ解: 因为 ∠ADB=∠EDC, ?
∠ABC=∠ECD=90°, ? 所以 △ABD∽△ECD, ?
答: 两岸间的大致距离为100米. ?应用举例2WXQ 我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。此时如果测得BD=45米,
DE=90米,BC=60米,
求两岸间的大致距离AB.一题多解WXQ1、如图,测得BD=120m,DC=60m,EC=50m,求河宽AB。解:∵∠B=∠C=90°,
∠ADB=∠EDC,
∴△ABD∽△ECD,
∴ AB:EC=BD:DC
∴ AB=50×120÷60
=100(m)
ABDCE应用感悟2WXQ2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=35m,DC=35m,DE=30m,那么你能算出池塘的宽AB吗?应用感悟2WXQ1. 相似三角形的应用主要有两个方面:(1) 测高 测量不能到达两点间的距离,常构造相似三角形求解。(不能直接使用皮尺或刻度尺量的)(不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。(2) 测距课堂小结2. 解相似三角形实际问题的一般步骤:审题 构建图形 利用相似解决问题WXQ1.小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为 米.WXQ2.数学兴趣小组测校内一棵树高,如图,把镜子放在离树(AB)8M点E处,然后沿着直线BE后退到D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2M,观察者目高CD=1.6M。树高多少米?WXQ3、如图,已知零件的外径a为25cm ,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=3,且量得CD=7cm,求厚度x。O(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。)WXQ4、 已知左、右并排的两棵大树的高分别是
AB=8m和CD=12m,两树的根部的距离
BD=5m,一个身高1.6m的人沿着正
对这两棵树的一条水平直路l从左
向右前进,当他与左边较低的树的距离小于多少时,
就不能看到右边较高的树的顶端点C?
设观察者眼晴的位置(视点)
为F,∠CFK和∠AFH分别是
观察点C、A的仰角,区域Ⅰ
和区域Ⅱ都在观察者看不到
的区域(盲区)之内。WXQ解:假设观察者从左向右走到点E时,他的眼睛的
位置点F与两棵树的顶端点A、C在一条直线上。
∵AB⊥l,CD⊥l,
∴AB∥CD,△AFH∽△CFK,
∴FH:FK=AH:CK,
即
,
解得FH=8.当他与左边较低的树的距离小
于8m时,就不能看到右边较高
的树的顶端点C。
WXQ5.教学楼旁边有一棵树,数学兴趣小组的同学们想利用树影测量树高。课外活动时在阳光下他们测得一根长为1米的竹竿的影长是0.9米,但当他们马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上。他们测得落在地面的影长2.7米,落在墙壁上的影长1.2米,请你和他们一起算一下,树高多少米?图11WXQ6、如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4.5m,如果小明得身高为1.5m,求路灯杆AB的高度。A
