高中物理沪教版(2019)选择性必修一 课件 2.3 摆钟的物理原理(共20张PPT)
文档属性
| 名称 | 高中物理沪教版(2019)选择性必修一 课件 2.3 摆钟的物理原理(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-28 14:52:22 | ||
图片预览






文档简介
(共20张PPT)
第二章 机械振动
3.摆钟的物理原理
生活中常可以看到悬挂起来的物体在竖直平面内摆动,他们在平衡位置附近的往复运动是不是简谐运动呢?
新课引入
1.定义:一根细线悬挂一个小球,如果细线的质量与小球的质量相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
惠更斯的科学抽象-单摆
一
2.单摆是理想化模型,实际摆看成单摆的条件:
①摆线质量与小球质量相比小很多, 忽略摆线的质量
②摆球所受阻力远小于摆球重力及绳的拉力,忽略空气阻力
③摆线的形变量比摆线长度小的多,忽略摆线形变 ④摆球的直径 d 远小于摆线的长度, 将摆球看作质点
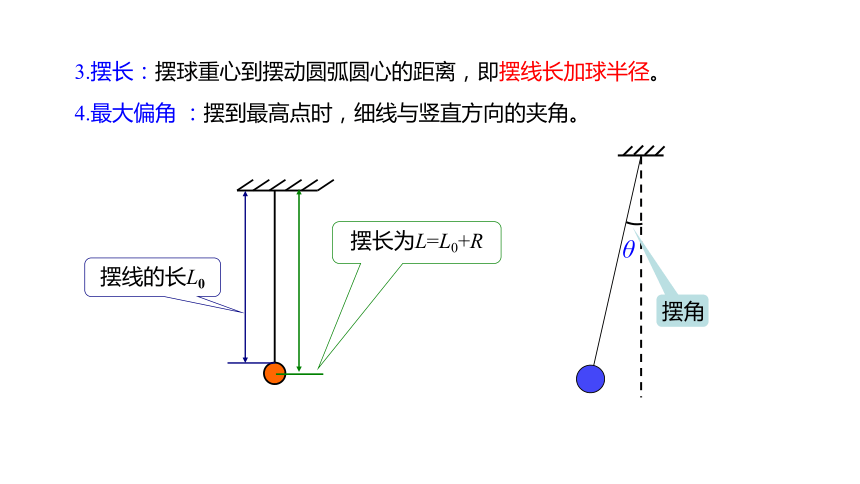
3.摆长:摆球重心到摆动圆弧圆心的距离,即摆线长加球半径。
4.最大偏角 :摆到最高点时,细线与竖直方向的夹角。
摆线的长L0
摆长为L=L0+R
θ
摆角
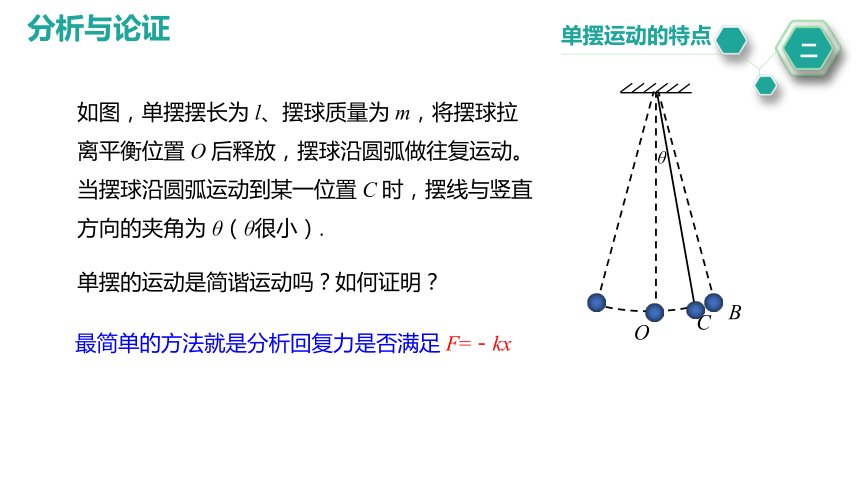
如图,单摆摆长为 l、摆球质量为 m,将摆球拉离平衡位置 O 后释放,摆球沿圆弧做往复运动。当摆球沿圆弧运动到某一位置 C 时,摆线与竖直方向的夹角为 θ(θ很小).
单摆运动的特点
二
分析与论证
单摆的运动是简谐运动吗?如何证明?
最简单的方法就是分析回复力是否满足 F=-kx
C
B
O
θ
对小球受力分析: F=G2=mgsinθ,
在偏角很小时,小球相对于最低点的位移为x,与所对应的弧长近似相等;
如果角 θ 很小,用弧度表示的 θ 与它的正弦 sin θ近似相等,即
联立得 ;
符合简谐运动的动力学特征,则小球做简谐运动。
C
B
O
θ
T
G
G2
G1
结论:在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动。
一般偏角 F k x (k )
角度 弧度值θ sin θ
5° 0.08727 0.08716
4° 0.06981 0.06976
3° 0.05236 0.05234
2° 0.03491 0.03490
1° 0.01754 0.01754
C
B
O
θ
1.所谓平衡位置,是指摆球静止时,摆线拉力与小球所受重力平衡的位置,并不是指摆动过程中摆球受力平衡的位置。摆球摆动到平衡位置时,回复力为零,但有指向悬点的向心力作用。
2.回复力是由摆球受到的重力沿圆弧切线方向的分力F= mgsinθ提供的,不可误认为回复力是重力和摆线拉力的合力。
特别提醒
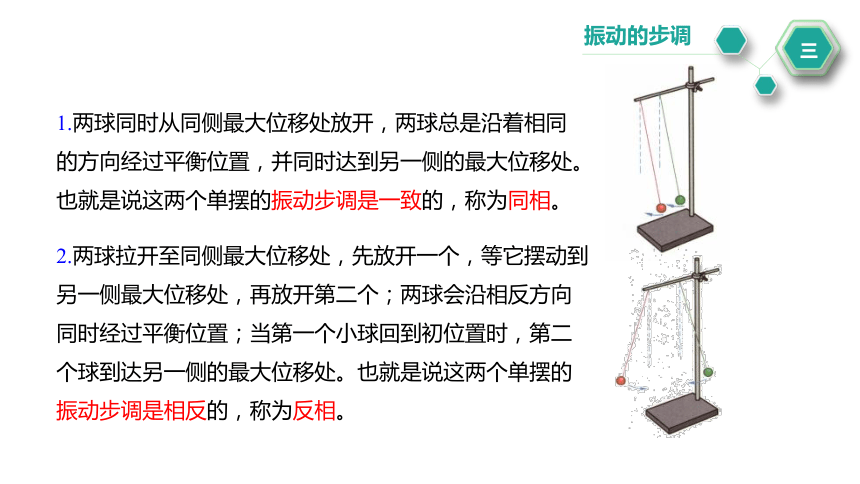
1.两球同时从同侧最大位移处放开,两球总是沿着相同的方向经过平衡位置,并同时达到另一侧的最大位移处。也就是说这两个单摆的振动步调是一致的,称为同相。
2.两球拉开至同侧最大位移处,先放开一个,等它摆动到另一侧最大位移处,再放开第二个;两球会沿相反方向同时经过平衡位置;当第一个小球回到初位置时,第二个球到达另一侧的最大位移处。也就是说这两个单摆的振动步调是相反的,称为反相。
二
振动的步调
三
3.相位:当(ωt+φ)确定时,x=Asin (ωt+φ)的函数值也就确定了,即物体做简谐运动的位置状态就确定了。物理学中把(ωt+φ)叫做相位。
φ是t=0时的相位,称为初相位或初相。
4.相位差:指两个简谐运动的相位之差,可以反映出两个简谐运动的步调差异,经常用到的是两个具有相同频率的简谐运动的相位差。
两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差
Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.
(1)若Δφ=( φ2 - φ1 )>0, 则2的相位比1的超前;
(2)若Δφ =( φ2 - φ1 )<0, 则2的相位比1的落后。
A与B的相位差为0,同相步调一致
B与C的相位差为π, 反相步调相反
特别提醒:
同相: Δφ=0时两运动步调完全相同
反相: Δφ=π(或-π)时,步调相反
例1 .下列有关单摆运动过程中的受力,说法正确的是( )
A.单摆运动的回复力是重力和摆线拉力的合力
B.单摆运动的回复力是重力沿圆弧切线方向的一个分力
C.单摆经过平衡位置时合力为零
D.单摆运动的回复力是摆线拉力的一个分力
典例分析
B
分析:单摆运动是在一段圆弧上运动,因此单摆运动过程不仅有回复力,而且有向心力,即单摆的合外力不仅要提供回复力,而且要提供向心力,故选项A错误;单摆的回复力是摆球所受重力沿圆弧切线方向的分力,而不是摆线拉力的分力,故选项B正确,D错误;单摆经过平衡位置时,回复力为零,向心力最大,故其合外力不为零,所以选项C错误.
例2 .(多选)如图所示,A、B分别为单摆做简谐运动时摆球的不同位置。其中,位置A为摆球摆动的最高位置,虚线为过悬点的竖直线.以摆球最低位置为重力势能零点,则摆球在摆动过程中( )
A.位于B处时动能最大
B.位于A处时势能最大
C.在位置A的势能大于在位置B的动能
D.在位置B的机械能大于在位置A的机械能
BC
分析:摆球摆到最低点时势能为零,动能最大,而B并非摆动中的最低位置,其动能并非最大,故A错; A为摆球摆动的最高位置,其势能最大,故B对;摆球在A处的势能等于总的机械能,在B处的动能小于总机械能(其中一部分为势能),故在位置A的势能大于在位置B的动能,故C对;摆球在摆动的过程中,只有重力做功,机械能守恒,故D错。
例3. (多选)一单摆做小角度摆动,其振动图象如图,以下说法正确的( )
A.t1时刻摆球速度最大,悬线对它的拉力最小
B.t2时刻摆球速度为零,悬线对它的拉力最小
C.t3时刻摆球速度为零,悬线对它的拉力最小
D.t4时刻摆球速度最大,悬线对它的拉力最大
CD
分析:单摆做小角度摆动时符合简谐运动的特点。
t1时刻摆球在位移最大处,回复力最大,加速度最大,速度为零,所以A项错误;t2时刻摆球的位移为零,回复力为零,加速度为零,速度达到最大,所以B项错误;t3时刻摆球在位移最大处,速度为零,向心力为零,对小球受力分析,重力的切向分力提供回复力,悬线的拉力等于重力的径向分力,此时拉力最小,所以C项正确;t4时刻摆球位移为零,回复力为零,加速度为零,速度最大,向心力最大,摆球运动到悬点的正下方,悬线的拉力减去竖直向下的重力的合力提供向心力,悬线拉力最大,所以D项正确。
跟踪练习
1. (多选)单摆是为了研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计 B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多 D.只要是单摆的运动就是一种简谐运动
ABC
分析:理想化的单摆是指摆线质量不计,摆线长度不伸缩,而摆球的直径比摆线长度要短的多;即摆球应选择体积小密度大的小球,故ABC正确;当单摆的摆角小于5°时,才能将其视为简谐运动,故并不是所有的单摆的运动都能看作是一种简谐运动,故D错误。故选:ABC.
2. (多选)一单摆做简谐运动,在偏角增大的过程中,摆球的 ( )
A.位移增大 B.速度增大
C.回复力增大 D.机械能增大
AC
分析:由简谐运动的特点可知,当偏角增大时,摆球偏离平衡位置的位移增大,故A正确;当偏角增大时,动能转化为重力势能,所以速度减小,故B错误;由回复力F=-kx 可知,位移增大,回复力增大,故C正确;单摆做简谐运动过程中只有重力做功,所以机械能守恒,故D错误。
3. (多选)有两个简谐运动的振动方程分别是: cm ,
cm ,下列说法正确的是( )
A.它们的振幅相同 B.它们的周期相同
C.它们的相位差恒定 D.它们的振动步调一致
分析:依据两个振动方程我们知道:方程1代表的振子振动振幅为3cm;圆频率为ω=2πf=100π,则f=50 Hz;初相为 ;方程2代表的振子振动振幅为5cm,圆频率为ω=2πf=100π,则f=50 Hz;初相为 .可知相位差为 ,因此它们的振动步调不一致.
BC
本节内容结束
第二章 机械振动
3.摆钟的物理原理
生活中常可以看到悬挂起来的物体在竖直平面内摆动,他们在平衡位置附近的往复运动是不是简谐运动呢?
新课引入
1.定义:一根细线悬挂一个小球,如果细线的质量与小球的质量相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
惠更斯的科学抽象-单摆
一
2.单摆是理想化模型,实际摆看成单摆的条件:
①摆线质量与小球质量相比小很多, 忽略摆线的质量
②摆球所受阻力远小于摆球重力及绳的拉力,忽略空气阻力
③摆线的形变量比摆线长度小的多,忽略摆线形变 ④摆球的直径 d 远小于摆线的长度, 将摆球看作质点
3.摆长:摆球重心到摆动圆弧圆心的距离,即摆线长加球半径。
4.最大偏角 :摆到最高点时,细线与竖直方向的夹角。
摆线的长L0
摆长为L=L0+R
θ
摆角
如图,单摆摆长为 l、摆球质量为 m,将摆球拉离平衡位置 O 后释放,摆球沿圆弧做往复运动。当摆球沿圆弧运动到某一位置 C 时,摆线与竖直方向的夹角为 θ(θ很小).
单摆运动的特点
二
分析与论证
单摆的运动是简谐运动吗?如何证明?
最简单的方法就是分析回复力是否满足 F=-kx
C
B
O
θ
对小球受力分析: F=G2=mgsinθ,
在偏角很小时,小球相对于最低点的位移为x,与所对应的弧长近似相等;
如果角 θ 很小,用弧度表示的 θ 与它的正弦 sin θ近似相等,即
联立得 ;
符合简谐运动的动力学特征,则小球做简谐运动。
C
B
O
θ
T
G
G2
G1
结论:在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动。
一般偏角 F k x (k )
角度 弧度值θ sin θ
5° 0.08727 0.08716
4° 0.06981 0.06976
3° 0.05236 0.05234
2° 0.03491 0.03490
1° 0.01754 0.01754
C
B
O
θ
1.所谓平衡位置,是指摆球静止时,摆线拉力与小球所受重力平衡的位置,并不是指摆动过程中摆球受力平衡的位置。摆球摆动到平衡位置时,回复力为零,但有指向悬点的向心力作用。
2.回复力是由摆球受到的重力沿圆弧切线方向的分力F= mgsinθ提供的,不可误认为回复力是重力和摆线拉力的合力。
特别提醒
1.两球同时从同侧最大位移处放开,两球总是沿着相同的方向经过平衡位置,并同时达到另一侧的最大位移处。也就是说这两个单摆的振动步调是一致的,称为同相。
2.两球拉开至同侧最大位移处,先放开一个,等它摆动到另一侧最大位移处,再放开第二个;两球会沿相反方向同时经过平衡位置;当第一个小球回到初位置时,第二个球到达另一侧的最大位移处。也就是说这两个单摆的振动步调是相反的,称为反相。
二
振动的步调
三
3.相位:当(ωt+φ)确定时,x=Asin (ωt+φ)的函数值也就确定了,即物体做简谐运动的位置状态就确定了。物理学中把(ωt+φ)叫做相位。
φ是t=0时的相位,称为初相位或初相。
4.相位差:指两个简谐运动的相位之差,可以反映出两个简谐运动的步调差异,经常用到的是两个具有相同频率的简谐运动的相位差。
两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差
Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.
(1)若Δφ=( φ2 - φ1 )>0, 则2的相位比1的超前;
(2)若Δφ =( φ2 - φ1 )<0, 则2的相位比1的落后。
A与B的相位差为0,同相步调一致
B与C的相位差为π, 反相步调相反
特别提醒:
同相: Δφ=0时两运动步调完全相同
反相: Δφ=π(或-π)时,步调相反
例1 .下列有关单摆运动过程中的受力,说法正确的是( )
A.单摆运动的回复力是重力和摆线拉力的合力
B.单摆运动的回复力是重力沿圆弧切线方向的一个分力
C.单摆经过平衡位置时合力为零
D.单摆运动的回复力是摆线拉力的一个分力
典例分析
B
分析:单摆运动是在一段圆弧上运动,因此单摆运动过程不仅有回复力,而且有向心力,即单摆的合外力不仅要提供回复力,而且要提供向心力,故选项A错误;单摆的回复力是摆球所受重力沿圆弧切线方向的分力,而不是摆线拉力的分力,故选项B正确,D错误;单摆经过平衡位置时,回复力为零,向心力最大,故其合外力不为零,所以选项C错误.
例2 .(多选)如图所示,A、B分别为单摆做简谐运动时摆球的不同位置。其中,位置A为摆球摆动的最高位置,虚线为过悬点的竖直线.以摆球最低位置为重力势能零点,则摆球在摆动过程中( )
A.位于B处时动能最大
B.位于A处时势能最大
C.在位置A的势能大于在位置B的动能
D.在位置B的机械能大于在位置A的机械能
BC
分析:摆球摆到最低点时势能为零,动能最大,而B并非摆动中的最低位置,其动能并非最大,故A错; A为摆球摆动的最高位置,其势能最大,故B对;摆球在A处的势能等于总的机械能,在B处的动能小于总机械能(其中一部分为势能),故在位置A的势能大于在位置B的动能,故C对;摆球在摆动的过程中,只有重力做功,机械能守恒,故D错。
例3. (多选)一单摆做小角度摆动,其振动图象如图,以下说法正确的( )
A.t1时刻摆球速度最大,悬线对它的拉力最小
B.t2时刻摆球速度为零,悬线对它的拉力最小
C.t3时刻摆球速度为零,悬线对它的拉力最小
D.t4时刻摆球速度最大,悬线对它的拉力最大
CD
分析:单摆做小角度摆动时符合简谐运动的特点。
t1时刻摆球在位移最大处,回复力最大,加速度最大,速度为零,所以A项错误;t2时刻摆球的位移为零,回复力为零,加速度为零,速度达到最大,所以B项错误;t3时刻摆球在位移最大处,速度为零,向心力为零,对小球受力分析,重力的切向分力提供回复力,悬线的拉力等于重力的径向分力,此时拉力最小,所以C项正确;t4时刻摆球位移为零,回复力为零,加速度为零,速度最大,向心力最大,摆球运动到悬点的正下方,悬线的拉力减去竖直向下的重力的合力提供向心力,悬线拉力最大,所以D项正确。
跟踪练习
1. (多选)单摆是为了研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计 B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多 D.只要是单摆的运动就是一种简谐运动
ABC
分析:理想化的单摆是指摆线质量不计,摆线长度不伸缩,而摆球的直径比摆线长度要短的多;即摆球应选择体积小密度大的小球,故ABC正确;当单摆的摆角小于5°时,才能将其视为简谐运动,故并不是所有的单摆的运动都能看作是一种简谐运动,故D错误。故选:ABC.
2. (多选)一单摆做简谐运动,在偏角增大的过程中,摆球的 ( )
A.位移增大 B.速度增大
C.回复力增大 D.机械能增大
AC
分析:由简谐运动的特点可知,当偏角增大时,摆球偏离平衡位置的位移增大,故A正确;当偏角增大时,动能转化为重力势能,所以速度减小,故B错误;由回复力F=-kx 可知,位移增大,回复力增大,故C正确;单摆做简谐运动过程中只有重力做功,所以机械能守恒,故D错误。
3. (多选)有两个简谐运动的振动方程分别是: cm ,
cm ,下列说法正确的是( )
A.它们的振幅相同 B.它们的周期相同
C.它们的相位差恒定 D.它们的振动步调一致
分析:依据两个振动方程我们知道:方程1代表的振子振动振幅为3cm;圆频率为ω=2πf=100π,则f=50 Hz;初相为 ;方程2代表的振子振动振幅为5cm,圆频率为ω=2πf=100π,则f=50 Hz;初相为 .可知相位差为 ,因此它们的振动步调不一致.
BC
本节内容结束
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
