高中物理沪教版(2019)选择性必修一 课件 4.4 用双缝干涉仪测量光的波长(共24张PPT)
文档属性
| 名称 | 高中物理沪教版(2019)选择性必修一 课件 4.4 用双缝干涉仪测量光的波长(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-28 17:42:12 | ||
图片预览








文档简介
(共24张PPT)
第四章 光及其应用
4.用双缝干涉仪测量光的波长
新课引入
1801年,托马斯·杨虽然成功地做了证实光的波动说的双缝干涉实验,但并没有被科学界所承认。
有一位牛顿微粒学说派的学术权威说,托马斯·杨的实验“没有任何价值”、“称不上实验”,干涉原理“荒唐”和“不合逻辑”……
托马斯·杨并没有因这些攻击而气馁,仍坚持他的研究,并于1803年,第一次用这个实验测出了光波的波长,再次肯定了光的波动性。
本节将采用与托马斯·杨类似的实验方法,测量光波的波长。
学习使用双缝干涉仪
一
知能提升
双缝
S1
S2
屏幕
什么是干涉条纹的间距(条纹宽度)
x
x
条纹间距的含义:相邻亮纹和亮纹之间的距离或暗纹和暗纹之间的距离叫做条纹间距。
我们所说的亮纹是指最亮的地方,暗纹是最暗的地方,从最亮到最暗有一个过渡,条纹间距实际上是最亮与最亮或最暗与最暗之间的距离。
测量波长公式的推导
二
知能提升
如图所示,双缝间距为d,双缝到屏的距离为l。双缝S1、S2的连线的中垂线与屏的交点为P 。对屏上与P距离为x的一点 P1,两缝与P1的距离P1 S1=r1, P1 S2=r2。
S1
S2
P1
P
l
d
x
r2
r1
M
当两列波的路程差为波长的整数倍,即
相邻两个明(或暗)条纹之间的距离为:
在线段P1 S2上作P1 M= P1 S1,则S2M=r2-r1,
因d l,三角形S1S2M可看做直角三角形
有:r2-r1=dsin θ(令∠S2S1M=θ) ①
另:x=l tan θ≈lsin θ ②
时才会出现亮条纹,
亮条纹位置为:
(1)用双缝干涉实验装置测量光的波长;
(2)学习测量微小距离的方法。
实验目的:
实验器材:
用双缝干涉测量光的波长
三
单色光通过单缝后,经双缝产生稳定的干涉图样,图样中相邻两条亮(暗)纹间的距离x与双缝间的距离d、双缝到屏的距离L、单色光的波长λ之间满足:
, 转换得到公式:
实验原理与设计:
实验步骤:
(1)如图所示,在光具座上把各光学元件装配好。从遮光筒上取下双缝,打开电源,调节光源的高度,直到光束能沿遮光筒的轴线射到毛玻璃屏的中心。放上单缝和双缝,使它们的距离为5 ~10 cm,并保持缝相互平行。注意各光学元件中心应大致位于遮光筒的轴线上。
(2)观察光屏上的白光干涉条纹的特点。给光源加上不同的滤光片,看条纹的色彩、间距发生了什么变化,相邻亮条纹(或暗条纹)的间距是否相等。
(3)l 的测量:双缝到屏的距离l 可以用刻度尺测出。d 的测量:在双缝上读出
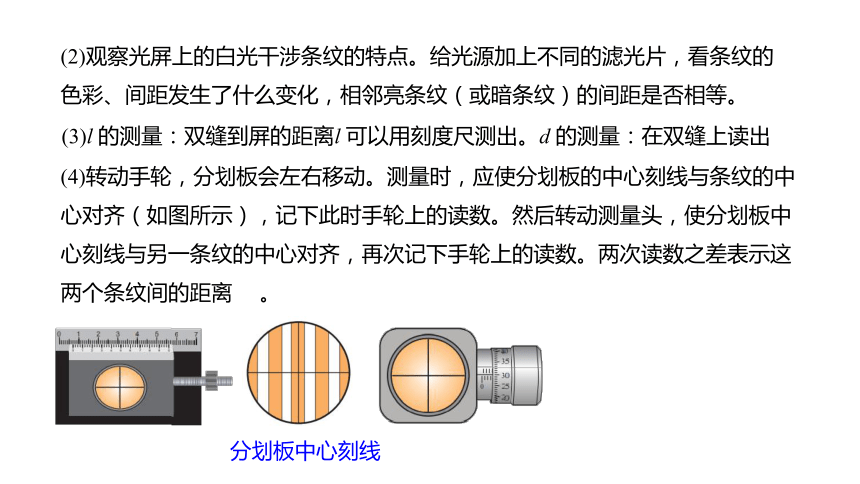
(4)转动手轮,分划板会左右移动。测量时,应使分划板的中心刻线与条纹的中心对齐(如图所示),记下此时手轮上的读数。然后转动测量头,使分划板中心刻线与另一条纹的中心对齐,再次记下手轮上的读数。两次读数之差表示这两个条纹间的距离 。
分划板中心刻线
为了减小测量误差,可测多个亮条纹间的距离,再求出相邻两个条纹间的距离。例如,可测出 n 个亮条纹间的距离 a,再求出相邻两个亮条纹间的距离 。
第1条亮纹的示数
第n条亮纹的示数
设计表格记录实验数据。d 是已知的,l 和 n 条亮条纹间的距离 a 是直接测量值。
由
可以求出相邻两个亮条纹间的距离 。
最后,根据
算出波长。
注意事项:
实验前先取下双缝,打开光源,调节光源的高度和角度,使它发出的光束沿着遮光筒的轴线把屏照亮。然后放好单缝和双缝。注意使单缝与双缝相互平行,尽量使缝的中点位于遮光筒的轴线上。
红
双缝到屏的距离L
n条亮(或暗)条纹的距离a
(1)若测定红光的波长,应选用____色的滤光片.实验时需要测定的物理量有:_________________________和________________________________.
例.在“用双缝干涉测光的波长”的实验中,装置如下图所示。双缝间的距离d=3 mm.
典例精析
(2)若测得双缝与屏之间距离为0.70 m,通过测量头(与螺旋测微器原理相似,手轮转动一周,分划板前进或后退0.500 mm)观察到第1条亮纹的位置如下图(a)所示,观察第5条亮纹的位置如下图(b)所示.则可求出红光的波长λ=_________m.(保留一位有效数字)
示数为0
0.650mm
7×10-7
一、学习使用双缝干涉仪
二、测量波长公式的推导
课堂小结
三、实验原理与设计
四、实验步骤与数据分析
1.(多选)某同学在做双缝干涉实验时,安装好实验装置,在光屏上却观察不到干涉图样,这可能是由于( )
A.光束的中央轴线与遮光筒的轴线不一致,相差较大
B.滤光片、单缝、双缝的中心在同一高度
C.单缝与双缝不平行
D.光源发出的光束太强
解析:光束的中央轴线与遮光筒的轴线不一致,单、双缝不平行都可能造成看不到干涉图样。选项A、C正确。
AC
跟踪练习
2.(多选)某同学按实验装置安装好仪器后,观察光的干涉现象,获得成功。若他在此基础上对仪器的安装有如下改动,则仍能使实验成功的是( )
A.将遮光筒的光屏向靠近双缝的方向移动少许,其他不动
B.将滤光片移至单缝和双缝之间,其他不动
C.将单缝向双缝移动少许,其他不动
D.将单缝与双缝的位置互换,其他不动
解析:干涉条纹是双缝发出的光叠加的结果,双缝后面的区域处处存在光,所以移动光屏或改变单缝与双缝间距,条纹仍然形成,故A、C正确;将滤光片移至单缝和双缝之间,照到双缝上的光仍是振动情况完全一样的光源,故B正确;将单缝与双缝的位置互换,失去了产生干涉的条件,故D错误。
ABC
3.在杨氏双缝干涉实验中,如果( )
A.用白光作为光源, 屏上将呈现黑白相间的条纹
B.用红光作为光源, 屏上将呈现红黑相间的条纹
C.用红光照射一条狭缝,用紫光照射另一条狭缝,屏上将呈现彩色条纹
BD
解析:白光作杨氏双缝干涉实验,屏上将呈现彩色条纹,A错;用红光作光源,屏上将呈现红色亮条纹与暗条纹(即黑条纹)相间,B对;红光和紫光频率不同,不能产生干涉条纹,C错。
4.双缝干涉测光的波长的实验装置如图甲所示,已知单缝与双缝间的距离l1=100 mm,双缝与屏的距离l2=700 mm,双缝间距d=0.25 mm。用测量头来测量亮纹中心的距离。测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻线对准亮纹的中心(如图乙所示),记下此时手轮上的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的读数。
(1)分划板的中心刻线分别对准第1条和第4条亮纹的中心时,手轮上的读数如图丙所示,则对准第1条时读数x1= mm,对准第4条时读数x2= mm。
(2)写出计算波长λ的表达式,λ= (用符号表示),λ= m。
解析:(1)读数x1=2 mm+0.01×19.0 mm=2.190 mm,
x2=7.5 mm+0.01×37.0 mm=7.870 mm。
(2)相邻两亮条纹中心间距Δx=由Δx=λ
可得λ=Δx· m=6.762×10-7 m。
答案:(1)2.190 7.870 (2) 6.762×10-7
5.在用双缝干涉测光的波长实验中,将双缝干涉实验仪按要求安装在光具座上(如图甲所示),并选用缝间距d=0.20 mm 的双缝屏。从仪器注明的规格可知,像屏与双缝屏间的距离l=700 mm。然后,接通电源使光源正常工作。
甲
(1)已知测量头主尺的最小刻度是毫米,副尺上有50分度。某同学调整手轮后,从测量头的目镜看去,第一次映入眼帘的干涉条纹如图乙(a)所示,图乙(a)中的数字是该同学给各暗纹的编号,此时图乙(b)中游标尺上的读数x1=1.16 mm;接着再转动手轮,映入眼帘的干涉条纹如图丙(a)所示,此时图丙(b)中游标尺上的读数x2= mm。
乙
丙
15.02
(2)利用上述测量结果,经计算可得两个相邻明纹(或暗纹)间的距离Δx= mm;这种色光的波长λ= nm。
解析:由题图知,4号条纹移动了6个条纹间距的宽度,
则有Δx= mm=2.31 mm;
再由Δx=λ,可求出 λ= mm=6.6×102 nm。
2.31
6.6×102
本节内容结束
第四章 光及其应用
4.用双缝干涉仪测量光的波长
新课引入
1801年,托马斯·杨虽然成功地做了证实光的波动说的双缝干涉实验,但并没有被科学界所承认。
有一位牛顿微粒学说派的学术权威说,托马斯·杨的实验“没有任何价值”、“称不上实验”,干涉原理“荒唐”和“不合逻辑”……
托马斯·杨并没有因这些攻击而气馁,仍坚持他的研究,并于1803年,第一次用这个实验测出了光波的波长,再次肯定了光的波动性。
本节将采用与托马斯·杨类似的实验方法,测量光波的波长。
学习使用双缝干涉仪
一
知能提升
双缝
S1
S2
屏幕
什么是干涉条纹的间距(条纹宽度)
x
x
条纹间距的含义:相邻亮纹和亮纹之间的距离或暗纹和暗纹之间的距离叫做条纹间距。
我们所说的亮纹是指最亮的地方,暗纹是最暗的地方,从最亮到最暗有一个过渡,条纹间距实际上是最亮与最亮或最暗与最暗之间的距离。
测量波长公式的推导
二
知能提升
如图所示,双缝间距为d,双缝到屏的距离为l。双缝S1、S2的连线的中垂线与屏的交点为P 。对屏上与P距离为x的一点 P1,两缝与P1的距离P1 S1=r1, P1 S2=r2。
S1
S2
P1
P
l
d
x
r2
r1
M
当两列波的路程差为波长的整数倍,即
相邻两个明(或暗)条纹之间的距离为:
在线段P1 S2上作P1 M= P1 S1,则S2M=r2-r1,
因d l,三角形S1S2M可看做直角三角形
有:r2-r1=dsin θ(令∠S2S1M=θ) ①
另:x=l tan θ≈lsin θ ②
时才会出现亮条纹,
亮条纹位置为:
(1)用双缝干涉实验装置测量光的波长;
(2)学习测量微小距离的方法。
实验目的:
实验器材:
用双缝干涉测量光的波长
三
单色光通过单缝后,经双缝产生稳定的干涉图样,图样中相邻两条亮(暗)纹间的距离x与双缝间的距离d、双缝到屏的距离L、单色光的波长λ之间满足:
, 转换得到公式:
实验原理与设计:
实验步骤:
(1)如图所示,在光具座上把各光学元件装配好。从遮光筒上取下双缝,打开电源,调节光源的高度,直到光束能沿遮光筒的轴线射到毛玻璃屏的中心。放上单缝和双缝,使它们的距离为5 ~10 cm,并保持缝相互平行。注意各光学元件中心应大致位于遮光筒的轴线上。
(2)观察光屏上的白光干涉条纹的特点。给光源加上不同的滤光片,看条纹的色彩、间距发生了什么变化,相邻亮条纹(或暗条纹)的间距是否相等。
(3)l 的测量:双缝到屏的距离l 可以用刻度尺测出。d 的测量:在双缝上读出
(4)转动手轮,分划板会左右移动。测量时,应使分划板的中心刻线与条纹的中心对齐(如图所示),记下此时手轮上的读数。然后转动测量头,使分划板中心刻线与另一条纹的中心对齐,再次记下手轮上的读数。两次读数之差表示这两个条纹间的距离 。
分划板中心刻线
为了减小测量误差,可测多个亮条纹间的距离,再求出相邻两个条纹间的距离。例如,可测出 n 个亮条纹间的距离 a,再求出相邻两个亮条纹间的距离 。
第1条亮纹的示数
第n条亮纹的示数
设计表格记录实验数据。d 是已知的,l 和 n 条亮条纹间的距离 a 是直接测量值。
由
可以求出相邻两个亮条纹间的距离 。
最后,根据
算出波长。
注意事项:
实验前先取下双缝,打开光源,调节光源的高度和角度,使它发出的光束沿着遮光筒的轴线把屏照亮。然后放好单缝和双缝。注意使单缝与双缝相互平行,尽量使缝的中点位于遮光筒的轴线上。
红
双缝到屏的距离L
n条亮(或暗)条纹的距离a
(1)若测定红光的波长,应选用____色的滤光片.实验时需要测定的物理量有:_________________________和________________________________.
例.在“用双缝干涉测光的波长”的实验中,装置如下图所示。双缝间的距离d=3 mm.
典例精析
(2)若测得双缝与屏之间距离为0.70 m,通过测量头(与螺旋测微器原理相似,手轮转动一周,分划板前进或后退0.500 mm)观察到第1条亮纹的位置如下图(a)所示,观察第5条亮纹的位置如下图(b)所示.则可求出红光的波长λ=_________m.(保留一位有效数字)
示数为0
0.650mm
7×10-7
一、学习使用双缝干涉仪
二、测量波长公式的推导
课堂小结
三、实验原理与设计
四、实验步骤与数据分析
1.(多选)某同学在做双缝干涉实验时,安装好实验装置,在光屏上却观察不到干涉图样,这可能是由于( )
A.光束的中央轴线与遮光筒的轴线不一致,相差较大
B.滤光片、单缝、双缝的中心在同一高度
C.单缝与双缝不平行
D.光源发出的光束太强
解析:光束的中央轴线与遮光筒的轴线不一致,单、双缝不平行都可能造成看不到干涉图样。选项A、C正确。
AC
跟踪练习
2.(多选)某同学按实验装置安装好仪器后,观察光的干涉现象,获得成功。若他在此基础上对仪器的安装有如下改动,则仍能使实验成功的是( )
A.将遮光筒的光屏向靠近双缝的方向移动少许,其他不动
B.将滤光片移至单缝和双缝之间,其他不动
C.将单缝向双缝移动少许,其他不动
D.将单缝与双缝的位置互换,其他不动
解析:干涉条纹是双缝发出的光叠加的结果,双缝后面的区域处处存在光,所以移动光屏或改变单缝与双缝间距,条纹仍然形成,故A、C正确;将滤光片移至单缝和双缝之间,照到双缝上的光仍是振动情况完全一样的光源,故B正确;将单缝与双缝的位置互换,失去了产生干涉的条件,故D错误。
ABC
3.在杨氏双缝干涉实验中,如果( )
A.用白光作为光源, 屏上将呈现黑白相间的条纹
B.用红光作为光源, 屏上将呈现红黑相间的条纹
C.用红光照射一条狭缝,用紫光照射另一条狭缝,屏上将呈现彩色条纹
BD
解析:白光作杨氏双缝干涉实验,屏上将呈现彩色条纹,A错;用红光作光源,屏上将呈现红色亮条纹与暗条纹(即黑条纹)相间,B对;红光和紫光频率不同,不能产生干涉条纹,C错。
4.双缝干涉测光的波长的实验装置如图甲所示,已知单缝与双缝间的距离l1=100 mm,双缝与屏的距离l2=700 mm,双缝间距d=0.25 mm。用测量头来测量亮纹中心的距离。测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻线对准亮纹的中心(如图乙所示),记下此时手轮上的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的读数。
(1)分划板的中心刻线分别对准第1条和第4条亮纹的中心时,手轮上的读数如图丙所示,则对准第1条时读数x1= mm,对准第4条时读数x2= mm。
(2)写出计算波长λ的表达式,λ= (用符号表示),λ= m。
解析:(1)读数x1=2 mm+0.01×19.0 mm=2.190 mm,
x2=7.5 mm+0.01×37.0 mm=7.870 mm。
(2)相邻两亮条纹中心间距Δx=由Δx=λ
可得λ=Δx· m=6.762×10-7 m。
答案:(1)2.190 7.870 (2) 6.762×10-7
5.在用双缝干涉测光的波长实验中,将双缝干涉实验仪按要求安装在光具座上(如图甲所示),并选用缝间距d=0.20 mm 的双缝屏。从仪器注明的规格可知,像屏与双缝屏间的距离l=700 mm。然后,接通电源使光源正常工作。
甲
(1)已知测量头主尺的最小刻度是毫米,副尺上有50分度。某同学调整手轮后,从测量头的目镜看去,第一次映入眼帘的干涉条纹如图乙(a)所示,图乙(a)中的数字是该同学给各暗纹的编号,此时图乙(b)中游标尺上的读数x1=1.16 mm;接着再转动手轮,映入眼帘的干涉条纹如图丙(a)所示,此时图丙(b)中游标尺上的读数x2= mm。
乙
丙
15.02
(2)利用上述测量结果,经计算可得两个相邻明纹(或暗纹)间的距离Δx= mm;这种色光的波长λ= nm。
解析:由题图知,4号条纹移动了6个条纹间距的宽度,
则有Δx= mm=2.31 mm;
再由Δx=λ,可求出 λ= mm=6.6×102 nm。
2.31
6.6×102
本节内容结束
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
