北师大版五年级上册第三单元倍数与因数(知识梳理+提高训练)(含答案)
文档属性
| 名称 | 北师大版五年级上册第三单元倍数与因数(知识梳理+提高训练)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 437.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版五年级上册第三单元倍数与因数(知识梳理+提高训练)二
知识点一:倍数与因数
1、倍数与因数的意义。
(1)如果a×b=c(A.B.c都是不为0的自然数),那么a和b就是c的因数,c就是a和b的倍数,倍数与因数是乘法算式中积和乘数的关系,是相互依存的,没有倍数就不存在因数,没有因数也不存在倍数,不能单独说一个数是倍数或因数。
(2)一个数的倍数大于或等于这个数的因数,一个数的因数小于或等于这个数的倍数。
(3)只在自然数(0除外)的范围内研究倍数和因数。
2、求一个数的倍数的方法。
用这个数分别乘1,2,3,4,…所得的积都是这个数的倍数。
3、判断两个数成倍数关系的方法。
(1)列乘法算式,用积判断。
(2)列除法算式,如果商是整数且没有余数就是倍数关系,反之不是。
知识点二:探索活动:2、5的倍数的特征
1、2的倍数的特征。
位上是0,2,4,6,8的数都是2的倍数。
2、5的倍数的特征。
个位上是0或5的数,都是5的倍数。判断一个数是不是5的倍数,就看这个数的个位上是不是0或5。
3、偶数和奇数。
像2,4,6,8,…这样的数,是2的倍数,叫作偶数。
像1,3,5,7,…这样的数,不是2的倍数,叫作奇数。
4、同时是2,5的倍数的特征。
个位上是0的数。
知识点三:探索活动:3的倍数的特征
1、一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
2、同时是2,3的倍数的特征。
个位上的数必须是0,2,4,6,8且各个数位上数字之和是3的倍数。
3、同时是3和5的倍数的特征。
个位上必须是0或5,且各个数位上数字之和是3的倍数。
4、同时是2、3、5的倍数的特征。
各个数位上数字之和是3的倍数,且个位上是0。
知识点四:找因数
1、找一个数的全部因数,看哪两个数相乘等于这个数,这两个数就是这个数的因数。
2、最小因数都是1。
3、最大因数是自己。
4、写出一个数的全部因数要按顺序从小到大写出,做到不重复,不遗漏。
5、因数在实际生活中应用很多,如装修房子时粘地板砖,需要 根据地板砖的大小计算粘几行、几列,学生们战队的时候要计算站几行,每行几人等。
知识点五:找质数
1、质数。
一个数只有1和它本身两个因数,这个数叫作质数。最小的质数是2。
2、一个数除了1和它本身以外还有别的因数,这个数叫作合数。最小的合数是4。
3、判断一个数是质数还是合数的方法:看这个数的因数的个数,只有2个因数的数是质数,有3个或3个以上因数的数是合数。
4、100以内的质数:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,共25个。
一、选择题(共16分)
1.在下面各组数中,第二个数是第一个数的因数的是( )。
A.12和36 B.5 和 7 C.18和 9 D.16 和 9
2.一个比1大的数除了1和它本身之外,没有其他的因数,这个数是( )。
A.质数 B.合数 C.奇数 D.偶数
3.要使四位数43□□同时是2、3、5的倍数,这个数可能是( )。
A.4310 B.4320 C.4330 D.4340
4.小华行李箱上密码锁的密码是1□44,这个数是3的倍数,她忘记了密码中的一个数字,这个密码一共有( )种可能。
A.2 B.4 C.3 D.5
5.要使三位数35□是3的倍数,方框里的填法有( )种。
A.1 B.2 C.3 D.4
6.边长为整数厘米,面积为165平方厘米的形状不相同的长方形共有( )种。
A.2 B.3 C.4 D.无数
7.在108、97、2、9873、1、360、75这七个数中,合数有( )个。
A.3 B.4 C.5 D.6
8.“任何一个大于2的偶数都可以表示成两个质数之和。”下列式子中能表达这个猜想的是( )。
A. B. C. D.
二、填空题(共16分)
9.一个数既是21的倍数,又是21的因数,这个数是( )。
10.猜数游戏。
我俩是( )和( )。
11.一个九位数最高位是最小的合数,千万位上是5的倍数,万位上是最小的质数,其余各位上都是0,这个数写作( ),省略亿后面的尾数约是( )。
12.把24个球装在盒子里(所有的球不能同时装在1个盒子里),每个盒子装得同样多,有( )种装法,最少需要( )个盒子。
13.一个长方形的面积是18平方厘米,如果长和宽都是自然数,这样的长方形有( )个,其中周长最短的一个是( )厘米。
14.一个三位数(各个数位上的数字不相同),百位上的数字既是质数又是偶数,个位上的数字既不是质数也不是合数,十位上的数字既不是正数又不负数。则这个数是( )。
15.同时是2、3和5的倍数的最小两位自然数是( )。
16.某表演队72人需要安排队列,要求每列或每行不少于3人且每行的人数要比每列的人数少,那么有( ) 种排法。
三、判断题(共8分)
17.12的所有因数中,有3个质数。( )
18.找因数可以通过加减法进行寻找。( )
19.100以内15的倍数有6个。( )
20.3个连续的自然数不可能都是合数。( )
四、连线题(共6分)
21.(6分)连一连。
五、作图题(共6分)
22.(6分)请在下面的方格纸上画出面积是20cm2的长方形(图中每个小方格的面积是1cm2),你有几种不同的画法?
六、解答题(共48分)
23.(6分)一个六位数,个位上是最小的质数,十位上是最小的合数,万位上的数既是质数又是偶数,十万位上的数是一位数中最大的自然数,其余数位上的数是0,这个六位数是多少?
24.(6分)李老师和同学们折纸鹤,每人折的只数相同,一共折了473只纸鹤。这个班有学生多少人?每人折纸鹤多少只?
25.(6分)小林和小华去看十四运的比赛,他们两个的座位号之和是20,差不超过10,已知他们的座位号都是质数,他们的座位号分别是多少?
26.(6分)五(1)班有32名同学参加广播操比赛,要使每行人数都相等,可以排几行?共有几种排法?(每行或每列不少于2人)
27.(6分)罗汉果茶具有清热润肺等功效。药店新到225个罗汉果,如果每2个包装成一袋,能正好包完吗?如果每5个包装成一袋呢?
28.(6分)张奶奶家摘了64个苹果,每5个装一袋,能正好装完吗?每2个装一袋,能正好装完吗?
29.(6分)一个三位数,百位上是最小的合数,十位上是最小的合数与最小的质数的商,个位上是最小的质数,写出这个三位数。
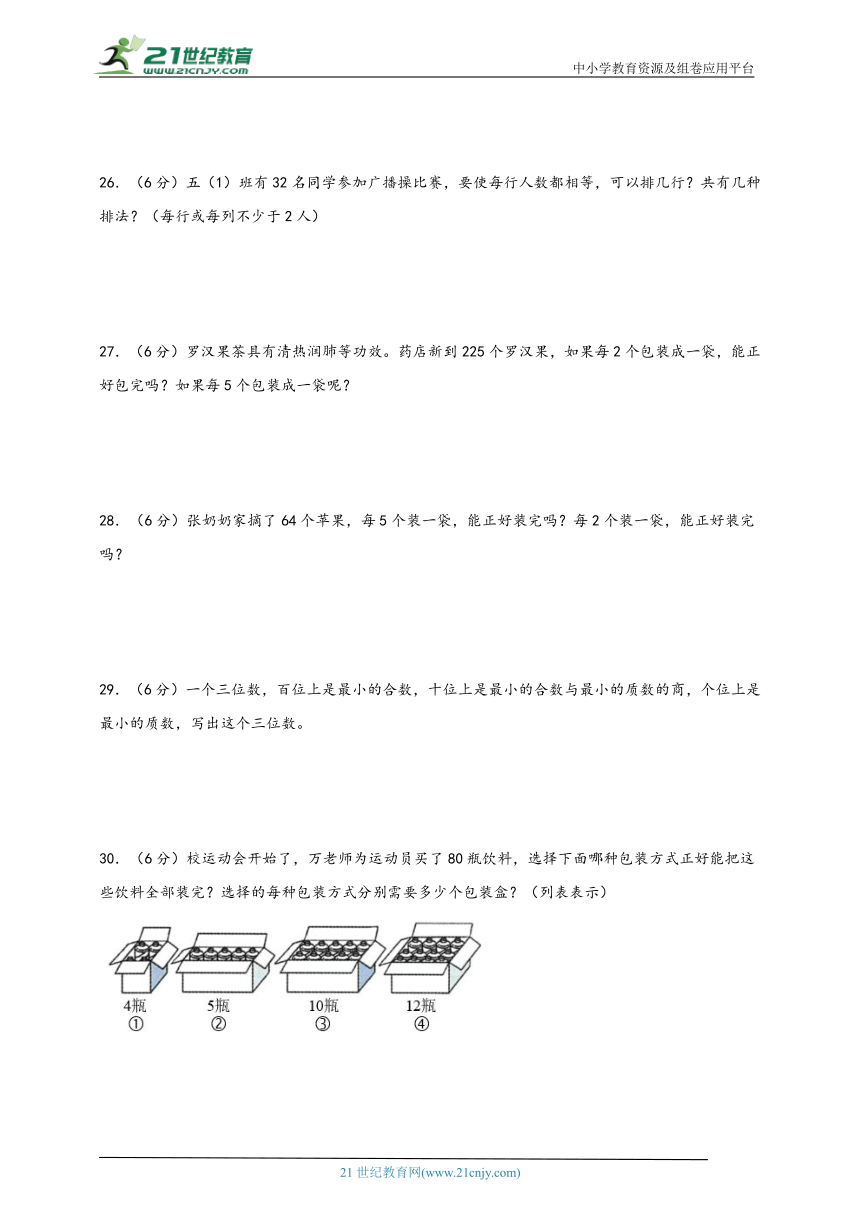
30.(6分)校运动会开始了,万老师为运动员买了80瓶饮料,选择下面哪种包装方式正好能把这些饮料全部装完?选择的每种包装方式分别需要多少个包装盒?(列表表示)
参考答案
1.C
【分析】根据因数和倍数的意义:如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;由此解答即可。
【详解】A.12和36;36÷12=3,36是12的倍数,不符合题意;
B.5和7;7÷5=1.4;1.4是小数,不符合因数的意义,不符合题意;
C.18和9;18÷9=2;18是9的倍数,9是18的因数,符合题意;
D.16和9;9÷18=0.5;0.5是小数,不符合因数的意义,不符合题意。
在下面各组数中,第二个数是第一个数的因数的是18和9。
故答案为:C
【点睛】解答此题的关键是根据因数和倍数的意义进行分析、解答即可。
2.A
【详解】根据质数和合数的概念:除了1和它本身以外,不含其它因数的数是质数;除了1和它本身外,还含有其它因数的数是合数;据此解答即可。由次可知:一个比1大的数除了1和它本身之外,没有其他的因数,这个数是质数;
故答案为:A
3.B
【分析】同时是2、3、5的倍数,则该四位数个位上是0且各数位上数字之和是3的倍数;据此逐项分析即可。
【详解】A.个位上是0,4+3+1+0=8,8不是3的倍数,所以4310不是3的倍数,不符合题意;
B.个位上是0,4+3+2+0=9,9是3的倍数,所以同时是2、3、5的倍数,符合题意;
C.个位上是0,4+3+3+0=10,10不是3的倍数,所以4330不是3的倍数,不符合题意;
D.个位上是0,4+3+4+0=11,11不是3的倍数,所以4340不是3的倍数,不符合题意;
故答案为:B
【点睛】本题主要考查2、3、5的倍数特征的灵活运用。
4.B
【分析】根据3的倍数的特征:各个数位上的数字之和是3的倍数;由此找出□内可能的数字。
【详解】□内如果是0;1+0+4+4=9;9能被3整数,是3的倍数,□内可能是0;
□内如果是1;1+1+4+4=10;10不能被3整除,不是3的倍数,□内不是1;
□内如果是2;1+2+4+4=11;11不能被3整除,不是3的倍数,□内不是2;
□内如果是3;1+3+4+4=12;12能被3整除,是3的倍数,□内可能是3;
□内如果是4;1+4+4+4=13;13不能被3整除,不是3的倍数,□内不是4;
□内如果是5;1+5+4+4=14;14不能被3整除,不是3的倍数,□内不是5;
□内如果是6;1+6+4+4=15;15能被3整除,是3的倍数,□内可能是6;
□内如果是7;1+7+4+4=16;16不能被3整除,不是3的倍数,□内不是7
□内如果是8;1+8+4+4=17;17不能被3整除,不是3的倍数,□内不是8;
□内如果是9;1+9+4+4=18;18能被3整除,是3 倍数,□内可能是9。
□内可能是0,3,6,9一共四种可能。
小华行李箱上密码锁的密码是1□44,这个数是3的倍数,她忘记了密码中的一个数字,这个密码一共有4种可能。
故答案为:B
【点睛】熟练掌握3的倍数特征是解答本题的关键。
5.C
【分析】3的倍数的特征:各个数位上的数字的和是3的倍数,这个数就是3的倍数。据此,3+5+1=9,3+5+4=12,3+5+7=15,9、12和15都是3的倍数,则三位数351、354、357是3的倍数。据此解答。
【详解】要使三位数35□是3的倍数,方框里可以填1、4或7,有3种填法。
故答案为:C
【点睛】掌握3的倍数的特征是解题的关键。
6.C
【分析】根据因数和倍数的意义,当a×b=c(a、b、c为非0自然数)我们说c是a和b的倍数,a和b是c的因数。据此可知长方形的长和宽是165的因数,根据长方形的面积=长×宽,列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数,能写出几组算式就是有几种这样的长方形。据此解答。
【详解】165=1×165=3×55=5×33=11×15
边长为整数厘米,面积为165平方厘米的形状不相同的长方形共有4种。
故答案为:C
【点睛】此题是考查因数的意义和找因数的方法,注意不要忽略a、b、c为非0自然数这点。
7.B
【分析】一个数除了1和它本身以外还有别的因数,这个数叫作合数;据此解答。
【详解】在108、97、2、9873、1、360、75这七个数中,合数有:108、9873、360、75共4个。
故答案为:B
【点睛】本题主要考查合数的意义,解题时注意1既不是质数也不是合数。
8.D
【分析】由题意知:“任何一个大于2的偶数都可以表示成两个质数之和。”包含两个信息,一是和数必须是偶数,二是和数等于两个质数相加。据此判断。
【详解】A.,1既不是质数也不是合数。说法错误。
B.,5不是偶数。说法错误。
C.,91不是质数,是合数。说法错误。
D.,20是偶数,7和13是质数。说法正确。
故答案为:D
【点睛】此题要反映这个猜想必须具备两个条件:一个是大于2的偶数,并且表示出两个此质数的和。
9.21
【分析】根据找一个数的因数的方法:一个数的因数是有限的,最大的因数是它本身,最小的因数是1;根据找一个数的倍数的方法,一个数的倍数是无限的,最小的一个倍数是它本身,可见一个数的本身既是其最大约数又是其最小倍数。
【详解】由分析得:
一个数既是21的倍数,又是21的因数,这个数是21。
【点睛】根据找一个数的因数、倍数的方法进行解答即可。
10. 5 7
【分析】根据题意,两个质数的积是35,则这两个数是35的质因数,那么把35分解质因数即可解答。
【详解】35=5×7,而5+7=12,则这两个数是5和7。
【点睛】掌握质因数和分解质因数的意义是解题的关键。
11. 450020000 5亿
【分析】一个数只有1和它本身两个因数,这个数叫做质数。一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。5的倍数特征:个位数是0或5;根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此可写出此数;省略“亿”后面的尾数就是四舍五入到亿位,再在数的后面写上“亿”字,据此写出。
【详解】最小的合数是4;5的倍数的一位数是5;最小的质数是2;
这个九位数写作:450020000;
450020000≈5亿
【点睛】本题主要考查了合数、质数、5的倍数认识以及整数的写法和近似数,注意整数的近似数要带计数单位。
12. 7 2
【分析】先找出24的所有因数,根据哪两个因数相乘是24,再根据这两个因数来确定每盒装几个,装几盒,注意所有的球不能同时装在1个盒子里。
【详解】24的因数有:1、2、3、4、6、8、12、24;装法有:
24=1×24,一盒24个,装1盒(排除);或每盒装1个,装24盒;
24=2×12,一盒装12个,装2盒;或每盒装2个,装12盒;
24=3×8,一盒装8个,装3盒;或每盒装3个,装8盒;
24=4×6,一盒装6个,装4盒;或每盒装4个,装6盒
所以有7种装法,最少需要2个盒子。
【点睛】此题主要考查求一个数的因数的方法,关键根据题意找出符合条件的数。
13. 3 18
【分析】长方形的面积=长×宽,则积是18的两个自然数就是长方形的长与宽;将数据代入长方形的周长公式:C=(a+b)×2求出最小值即可。
【详解】18=1×18=2×9=3×6
这样的长方形有长是18厘米宽是1厘米、长是9厘米宽是2厘米、长是6厘米宽是3厘米,共3个。
周长:(18+1)×2
=19×2
=38(厘米)
(9+2)×2
=11×2
=22(厘米)
(6+3)×2
=9×2
=18(厘米)
38>22>18
周长最小是18厘米。
综上可得:这样的长方形有3个,,其中周长最短的一个是18厘米。
【点睛】本题主要考查找一个数因数的方法。
14.201
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;除了1和它本身外,还有别的因数的数叫合数;不能被2整除的数叫做奇数,能被2整除的数叫做偶数;根据质数、合数、奇数和偶数的意义,0~9中,既是质数又是偶数的数是2,这个数的百位上的数是2;既不是质数也不是合数的数是1;这个数的个位上的数是1;正数:数字前面有“﹢”号或没有符号的数;负数:数字前面有“﹣”号的数,0既不是正数也不是负数;由此可知,这个数是十位上的数是0,这个数是201,据此解答。
【详解】根据分析可知,一个三位数(各个数位上的数字不相同),百位上的数字既是质数又是偶数,个位上的数字既不是质数也不是合数,十位上的数字既不是正数又不负数。则这个数是201。
【点睛】熟练掌握质数、合数、奇数、偶数、正数、负数的意义是解答本题的关键。
15.30
【分析】2的倍数特点:个位上是0、2、4、6、8,5的倍数特点:个位上是0或5,3的倍数特点:各个数位上数字之和是3的倍数,根据2、3、5的倍数特征可知,同时是2、3、5的倍数,个位上的数字是0,各个数位上的数字的和是3的倍数,据此解答即可。
【详解】同时是2、3和5的倍数的最小两位自然数是30。
【点睛】本题主要考查2、3、5的倍数特征,注意个位是0的数同时是2和5的倍数,3的倍数特征是:各个数位上的和是3的倍数,这个数就是3的倍数。
16.4
【分析】由于每行的人数×每列的人数=总人数,先找出72的因数,可以一对一对的找,进而根据题意确定可能每行排的人数和排的列数。
【详解】72的因数有:1,2,3,4,6,8,9,12,18,24,36,72。
因为每列或每行不少于3人,且每行的人数要比每列的人数少,因此符合这些条件的因数有:3,4,5,8,9,12,18,24。
每列24人,排3行;
每列18人,排4行;
每列12人,排6行;
每列9人,排8行。
一共有4种排法。
某表演队72人需要安排队列,要求每列或每行不少于3人且每行的人数要比每列的人数少,那么有4种排法。
【点睛】熟练掌握求一个数的因数的方法是解答本题的关键。
17.×
【分析】一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。根据求一个数的因数的方法求出12的因数;再根据质数的意义,一个自然数如果只有1和它本身两个因数,这样的数叫做质数。据此解答即可。
【详解】12的因数有1、2、3、4、6、12。
在这些因数中质数有2和3两个。
因此题干中的结论是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握求一个数的因数的方法及应用,质数的意义及应用。
18.×
【分析】找一个因数的方法:把一个因数写出两个整数相乘的形式,这两个整数就是这个数的因数,根据此方法即可找出这个数的所有因数。
【详解】由分析可知:
找因数是通过乘法进行寻找,原题说法错误。
故答案为:×
【点睛】本题主要考查找因数的方法,学会找因数的方法并灵活运用。
19.√
【分析】求一个数倍数的方法:用这个数分别乘自然数:1、2、3、4、5、……,就得到这个数的1倍、2倍、3倍、4倍、5倍、……据此求出100以内15的所有倍数即可。
【详解】15×1=15
15×2=30
15×3=45
15×4=60
15×5=75
15×6=90
15×7=105
100以内15的倍数有:15、30、45、60、75、90,共有6个。
故答案为:√
【点睛】列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。
20.×
【分析】根据合数的意义:除了1和它本身还有别的因数的数是合数;据此解答。
【详解】如3个连续的自然数:8、9、10(答案不唯一),都是合数;3个连续的自然数有可能都是合数。
原题干说法错误。
故答案为:×
【点睛】熟练掌握合数的意义是解答本题的关键。
21.见详解
【分析】根据质数与合数的意义,在自然数中,除了1和它本身外,没有别的因数的数为质数;除了1和它本身,还有别的因数的数为合数,据此解答。
【详解】
【点睛】本题考查质数与合数的意义,根据质数与合数的意义进行解答。
22.
【解析】略
23.这个六位数是920042
【分析】根据题意,逐一判断出每个数位上的数字各是多少,然后求出这个六位数是多少即可。
【详解】因为个位上是最小的质数
所以个位上是2
因为十位上是最小的合数
所以十位上是4
因为万位上的数既是质数又是偶数
所以万位上是2
因为十万位上的数是一位数中最大的自然数
所以十万位上是9
所以这个六位数是920042。
答:这个六位数是920042。
【点睛】(1)此题主要考查了整数的读法和写法,要熟练掌握,解答此题的关键是逐一判断出每个数位上的数字各是多少;
(2)此题还考查了奇数、偶数的特征,以及质数和合数的特征,要熟练掌握。
24.42人;11只
【分析】因为每人折纸鹤的只数乘这个班师生人数,可得一共折了多少只纸鹤,可得每人折纸鹤的只数和这个班师生人数都是473的因数,找出473的因数。再根据实际情况合理选定师生人数,最后再从师生人数中减去李老师1个人的人数即得这个班的学生人数。
【详解】473=11×43
根据实际情况可得学生有43―1=42(人)
答:这个班有学生42人,每人折纸鹤11只。
【点睛】本题主要考查了找一个数的因数的方法,关键是找出473的因数。
25.7号和13号
【分析】只有1和它本身两个因数的数叫做质数,据此分别写出和是20的两个数,再进行判断。
【详解】
在这几组加数中,只有3、17与7、13这两组数都是质数,又因为差不超过10,所以只有7、13符合题意。
答:他们的座位号分别是7号和13号。
【点睛】本题考查质数的应用。根据质数的意义找出符合题意的数是解题的关键。
26.2行、4行、8行、16行;4种
【分析】把32名同学平均分成若干行,那么行数和每行的人数相乘的积是32,根据找因数的方法,可以一对一的找,有多少个因数就有多少种排法,再结合题目进行分析即可。
【详解】由分析可得:
32=1×32,即每行1人,排32行,不符合题意;或者每行32人,排1行,不符合题意。
32=2×16,即每行2人,排16行;或每行16人,排2行;
32=4×8,即每行4人,排8行;或每行8人,排4行;
答:可以排2行、4行、8行、16行。共有4种排法。
【点睛】本题考查了找一个数因数的方法,解答此题的关键是把32分解因数,再对分解出来的因数结合题目进行分析,看是否需要排除。
27.如果每2个包装成一袋,不能正好包完;如果每5个包装成一袋,能正好包完
【分析】根据2的倍数特征:个位上是0、2、4,6,8的数都是2的倍数;5的倍数特征:个位上的数是0或5的数,是5的倍数,用225除以2,如果没有余数,正好包完,如果有余数,不能正好包完;同样再用225÷5,如果没有余数,正好包完,如果有余数,不能正好包完;据此解答。
【详解】225÷2=112(袋)……1(个),225不是2的倍数,
如果每2个包装成一袋,不能正好包完。
225÷5=45(袋),225是5的倍数;
如果每5个包装成一袋,能正好包完。
答:如果每2个包装成一袋,不能正好包完;如果每5个包装成一袋,能正好包完。
【点睛】熟练掌握2的倍数特征和5的倍数特征是解答本题的关键。
28.每5个装一袋,不能正好装完;每2个装一袋,能正好装完
【分析】根据2的倍数特征:个位上是0、2、4,6,8的数都是2的倍数;5的倍数特征:个位上的数是0或5的数,是5的倍数,再根据能被2,5整除的数的特征进行判断是否正好整完。
【详解】64÷5=12(袋)……4(个),64不能被5整除,不是5的倍数,不能正好装完;
64÷2=32(袋),64能被2整数,是2的倍数,能装好装完。
答:每5个装一袋,不能正好装完,每2个装一袋,能正好装完。
【点睛】熟练掌握2、5的倍数特征是解答本题的关键。
29.422
【分析】一个数,除了1和它本身,还有其他因数的数,叫做合数,最小的合数是4;一个数,只要1和它本身两个因数,这样的数叫做质数,最小的质数是2,据此解答。
【详解】最小的合数是4,百位上的数是4;
4÷2=2;十位上的数是2;
最小的质数是2,个位上的数是2。
这个数是422。
答:这个三位数是422。
【点睛】熟练掌握质数和合数的意义是解答本题的关键。
30.见详解
【分析】根据题意,只要求出每箱装饮料的数量是80的因数,即可解答。
【详解】①4瓶装:80÷4=20(个),可以用每箱4瓶装的包装盒;需要20个包装盒;
②5瓶装:80÷5=16(个),可以用每箱5瓶装的包装盒;需要16个包装盒;
③10瓶装:80÷10=8(个),可以用每箱10瓶装的包装盒;需要8个包装盒;
④12瓶装:80÷12≈6.6(个),不可以用每箱12瓶装的包装盒。
表如下:
包装方式 4瓶 5瓶 10瓶
包装盒数量 20个 16个 8个
【点睛】熟练掌握因数与倍数的关键是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版五年级上册第三单元倍数与因数(知识梳理+提高训练)二
知识点一:倍数与因数
1、倍数与因数的意义。
(1)如果a×b=c(A.B.c都是不为0的自然数),那么a和b就是c的因数,c就是a和b的倍数,倍数与因数是乘法算式中积和乘数的关系,是相互依存的,没有倍数就不存在因数,没有因数也不存在倍数,不能单独说一个数是倍数或因数。
(2)一个数的倍数大于或等于这个数的因数,一个数的因数小于或等于这个数的倍数。
(3)只在自然数(0除外)的范围内研究倍数和因数。
2、求一个数的倍数的方法。
用这个数分别乘1,2,3,4,…所得的积都是这个数的倍数。
3、判断两个数成倍数关系的方法。
(1)列乘法算式,用积判断。
(2)列除法算式,如果商是整数且没有余数就是倍数关系,反之不是。
知识点二:探索活动:2、5的倍数的特征
1、2的倍数的特征。
位上是0,2,4,6,8的数都是2的倍数。
2、5的倍数的特征。
个位上是0或5的数,都是5的倍数。判断一个数是不是5的倍数,就看这个数的个位上是不是0或5。
3、偶数和奇数。
像2,4,6,8,…这样的数,是2的倍数,叫作偶数。
像1,3,5,7,…这样的数,不是2的倍数,叫作奇数。
4、同时是2,5的倍数的特征。
个位上是0的数。
知识点三:探索活动:3的倍数的特征
1、一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
2、同时是2,3的倍数的特征。
个位上的数必须是0,2,4,6,8且各个数位上数字之和是3的倍数。
3、同时是3和5的倍数的特征。
个位上必须是0或5,且各个数位上数字之和是3的倍数。
4、同时是2、3、5的倍数的特征。
各个数位上数字之和是3的倍数,且个位上是0。
知识点四:找因数
1、找一个数的全部因数,看哪两个数相乘等于这个数,这两个数就是这个数的因数。
2、最小因数都是1。
3、最大因数是自己。
4、写出一个数的全部因数要按顺序从小到大写出,做到不重复,不遗漏。
5、因数在实际生活中应用很多,如装修房子时粘地板砖,需要 根据地板砖的大小计算粘几行、几列,学生们战队的时候要计算站几行,每行几人等。
知识点五:找质数
1、质数。
一个数只有1和它本身两个因数,这个数叫作质数。最小的质数是2。
2、一个数除了1和它本身以外还有别的因数,这个数叫作合数。最小的合数是4。
3、判断一个数是质数还是合数的方法:看这个数的因数的个数,只有2个因数的数是质数,有3个或3个以上因数的数是合数。
4、100以内的质数:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,共25个。
一、选择题(共16分)
1.在下面各组数中,第二个数是第一个数的因数的是( )。
A.12和36 B.5 和 7 C.18和 9 D.16 和 9
2.一个比1大的数除了1和它本身之外,没有其他的因数,这个数是( )。
A.质数 B.合数 C.奇数 D.偶数
3.要使四位数43□□同时是2、3、5的倍数,这个数可能是( )。
A.4310 B.4320 C.4330 D.4340
4.小华行李箱上密码锁的密码是1□44,这个数是3的倍数,她忘记了密码中的一个数字,这个密码一共有( )种可能。
A.2 B.4 C.3 D.5
5.要使三位数35□是3的倍数,方框里的填法有( )种。
A.1 B.2 C.3 D.4
6.边长为整数厘米,面积为165平方厘米的形状不相同的长方形共有( )种。
A.2 B.3 C.4 D.无数
7.在108、97、2、9873、1、360、75这七个数中,合数有( )个。
A.3 B.4 C.5 D.6
8.“任何一个大于2的偶数都可以表示成两个质数之和。”下列式子中能表达这个猜想的是( )。
A. B. C. D.
二、填空题(共16分)
9.一个数既是21的倍数,又是21的因数,这个数是( )。
10.猜数游戏。
我俩是( )和( )。
11.一个九位数最高位是最小的合数,千万位上是5的倍数,万位上是最小的质数,其余各位上都是0,这个数写作( ),省略亿后面的尾数约是( )。
12.把24个球装在盒子里(所有的球不能同时装在1个盒子里),每个盒子装得同样多,有( )种装法,最少需要( )个盒子。
13.一个长方形的面积是18平方厘米,如果长和宽都是自然数,这样的长方形有( )个,其中周长最短的一个是( )厘米。
14.一个三位数(各个数位上的数字不相同),百位上的数字既是质数又是偶数,个位上的数字既不是质数也不是合数,十位上的数字既不是正数又不负数。则这个数是( )。
15.同时是2、3和5的倍数的最小两位自然数是( )。
16.某表演队72人需要安排队列,要求每列或每行不少于3人且每行的人数要比每列的人数少,那么有( ) 种排法。
三、判断题(共8分)
17.12的所有因数中,有3个质数。( )
18.找因数可以通过加减法进行寻找。( )
19.100以内15的倍数有6个。( )
20.3个连续的自然数不可能都是合数。( )
四、连线题(共6分)
21.(6分)连一连。
五、作图题(共6分)
22.(6分)请在下面的方格纸上画出面积是20cm2的长方形(图中每个小方格的面积是1cm2),你有几种不同的画法?
六、解答题(共48分)
23.(6分)一个六位数,个位上是最小的质数,十位上是最小的合数,万位上的数既是质数又是偶数,十万位上的数是一位数中最大的自然数,其余数位上的数是0,这个六位数是多少?
24.(6分)李老师和同学们折纸鹤,每人折的只数相同,一共折了473只纸鹤。这个班有学生多少人?每人折纸鹤多少只?
25.(6分)小林和小华去看十四运的比赛,他们两个的座位号之和是20,差不超过10,已知他们的座位号都是质数,他们的座位号分别是多少?
26.(6分)五(1)班有32名同学参加广播操比赛,要使每行人数都相等,可以排几行?共有几种排法?(每行或每列不少于2人)
27.(6分)罗汉果茶具有清热润肺等功效。药店新到225个罗汉果,如果每2个包装成一袋,能正好包完吗?如果每5个包装成一袋呢?
28.(6分)张奶奶家摘了64个苹果,每5个装一袋,能正好装完吗?每2个装一袋,能正好装完吗?
29.(6分)一个三位数,百位上是最小的合数,十位上是最小的合数与最小的质数的商,个位上是最小的质数,写出这个三位数。
30.(6分)校运动会开始了,万老师为运动员买了80瓶饮料,选择下面哪种包装方式正好能把这些饮料全部装完?选择的每种包装方式分别需要多少个包装盒?(列表表示)
参考答案
1.C
【分析】根据因数和倍数的意义:如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;由此解答即可。
【详解】A.12和36;36÷12=3,36是12的倍数,不符合题意;
B.5和7;7÷5=1.4;1.4是小数,不符合因数的意义,不符合题意;
C.18和9;18÷9=2;18是9的倍数,9是18的因数,符合题意;
D.16和9;9÷18=0.5;0.5是小数,不符合因数的意义,不符合题意。
在下面各组数中,第二个数是第一个数的因数的是18和9。
故答案为:C
【点睛】解答此题的关键是根据因数和倍数的意义进行分析、解答即可。
2.A
【详解】根据质数和合数的概念:除了1和它本身以外,不含其它因数的数是质数;除了1和它本身外,还含有其它因数的数是合数;据此解答即可。由次可知:一个比1大的数除了1和它本身之外,没有其他的因数,这个数是质数;
故答案为:A
3.B
【分析】同时是2、3、5的倍数,则该四位数个位上是0且各数位上数字之和是3的倍数;据此逐项分析即可。
【详解】A.个位上是0,4+3+1+0=8,8不是3的倍数,所以4310不是3的倍数,不符合题意;
B.个位上是0,4+3+2+0=9,9是3的倍数,所以同时是2、3、5的倍数,符合题意;
C.个位上是0,4+3+3+0=10,10不是3的倍数,所以4330不是3的倍数,不符合题意;
D.个位上是0,4+3+4+0=11,11不是3的倍数,所以4340不是3的倍数,不符合题意;
故答案为:B
【点睛】本题主要考查2、3、5的倍数特征的灵活运用。
4.B
【分析】根据3的倍数的特征:各个数位上的数字之和是3的倍数;由此找出□内可能的数字。
【详解】□内如果是0;1+0+4+4=9;9能被3整数,是3的倍数,□内可能是0;
□内如果是1;1+1+4+4=10;10不能被3整除,不是3的倍数,□内不是1;
□内如果是2;1+2+4+4=11;11不能被3整除,不是3的倍数,□内不是2;
□内如果是3;1+3+4+4=12;12能被3整除,是3的倍数,□内可能是3;
□内如果是4;1+4+4+4=13;13不能被3整除,不是3的倍数,□内不是4;
□内如果是5;1+5+4+4=14;14不能被3整除,不是3的倍数,□内不是5;
□内如果是6;1+6+4+4=15;15能被3整除,是3的倍数,□内可能是6;
□内如果是7;1+7+4+4=16;16不能被3整除,不是3的倍数,□内不是7
□内如果是8;1+8+4+4=17;17不能被3整除,不是3的倍数,□内不是8;
□内如果是9;1+9+4+4=18;18能被3整除,是3 倍数,□内可能是9。
□内可能是0,3,6,9一共四种可能。
小华行李箱上密码锁的密码是1□44,这个数是3的倍数,她忘记了密码中的一个数字,这个密码一共有4种可能。
故答案为:B
【点睛】熟练掌握3的倍数特征是解答本题的关键。
5.C
【分析】3的倍数的特征:各个数位上的数字的和是3的倍数,这个数就是3的倍数。据此,3+5+1=9,3+5+4=12,3+5+7=15,9、12和15都是3的倍数,则三位数351、354、357是3的倍数。据此解答。
【详解】要使三位数35□是3的倍数,方框里可以填1、4或7,有3种填法。
故答案为:C
【点睛】掌握3的倍数的特征是解题的关键。
6.C
【分析】根据因数和倍数的意义,当a×b=c(a、b、c为非0自然数)我们说c是a和b的倍数,a和b是c的因数。据此可知长方形的长和宽是165的因数,根据长方形的面积=长×宽,列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数,能写出几组算式就是有几种这样的长方形。据此解答。
【详解】165=1×165=3×55=5×33=11×15
边长为整数厘米,面积为165平方厘米的形状不相同的长方形共有4种。
故答案为:C
【点睛】此题是考查因数的意义和找因数的方法,注意不要忽略a、b、c为非0自然数这点。
7.B
【分析】一个数除了1和它本身以外还有别的因数,这个数叫作合数;据此解答。
【详解】在108、97、2、9873、1、360、75这七个数中,合数有:108、9873、360、75共4个。
故答案为:B
【点睛】本题主要考查合数的意义,解题时注意1既不是质数也不是合数。
8.D
【分析】由题意知:“任何一个大于2的偶数都可以表示成两个质数之和。”包含两个信息,一是和数必须是偶数,二是和数等于两个质数相加。据此判断。
【详解】A.,1既不是质数也不是合数。说法错误。
B.,5不是偶数。说法错误。
C.,91不是质数,是合数。说法错误。
D.,20是偶数,7和13是质数。说法正确。
故答案为:D
【点睛】此题要反映这个猜想必须具备两个条件:一个是大于2的偶数,并且表示出两个此质数的和。
9.21
【分析】根据找一个数的因数的方法:一个数的因数是有限的,最大的因数是它本身,最小的因数是1;根据找一个数的倍数的方法,一个数的倍数是无限的,最小的一个倍数是它本身,可见一个数的本身既是其最大约数又是其最小倍数。
【详解】由分析得:
一个数既是21的倍数,又是21的因数,这个数是21。
【点睛】根据找一个数的因数、倍数的方法进行解答即可。
10. 5 7
【分析】根据题意,两个质数的积是35,则这两个数是35的质因数,那么把35分解质因数即可解答。
【详解】35=5×7,而5+7=12,则这两个数是5和7。
【点睛】掌握质因数和分解质因数的意义是解题的关键。
11. 450020000 5亿
【分析】一个数只有1和它本身两个因数,这个数叫做质数。一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。5的倍数特征:个位数是0或5;根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此可写出此数;省略“亿”后面的尾数就是四舍五入到亿位,再在数的后面写上“亿”字,据此写出。
【详解】最小的合数是4;5的倍数的一位数是5;最小的质数是2;
这个九位数写作:450020000;
450020000≈5亿
【点睛】本题主要考查了合数、质数、5的倍数认识以及整数的写法和近似数,注意整数的近似数要带计数单位。
12. 7 2
【分析】先找出24的所有因数,根据哪两个因数相乘是24,再根据这两个因数来确定每盒装几个,装几盒,注意所有的球不能同时装在1个盒子里。
【详解】24的因数有:1、2、3、4、6、8、12、24;装法有:
24=1×24,一盒24个,装1盒(排除);或每盒装1个,装24盒;
24=2×12,一盒装12个,装2盒;或每盒装2个,装12盒;
24=3×8,一盒装8个,装3盒;或每盒装3个,装8盒;
24=4×6,一盒装6个,装4盒;或每盒装4个,装6盒
所以有7种装法,最少需要2个盒子。
【点睛】此题主要考查求一个数的因数的方法,关键根据题意找出符合条件的数。
13. 3 18
【分析】长方形的面积=长×宽,则积是18的两个自然数就是长方形的长与宽;将数据代入长方形的周长公式:C=(a+b)×2求出最小值即可。
【详解】18=1×18=2×9=3×6
这样的长方形有长是18厘米宽是1厘米、长是9厘米宽是2厘米、长是6厘米宽是3厘米,共3个。
周长:(18+1)×2
=19×2
=38(厘米)
(9+2)×2
=11×2
=22(厘米)
(6+3)×2
=9×2
=18(厘米)
38>22>18
周长最小是18厘米。
综上可得:这样的长方形有3个,,其中周长最短的一个是18厘米。
【点睛】本题主要考查找一个数因数的方法。
14.201
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;除了1和它本身外,还有别的因数的数叫合数;不能被2整除的数叫做奇数,能被2整除的数叫做偶数;根据质数、合数、奇数和偶数的意义,0~9中,既是质数又是偶数的数是2,这个数的百位上的数是2;既不是质数也不是合数的数是1;这个数的个位上的数是1;正数:数字前面有“﹢”号或没有符号的数;负数:数字前面有“﹣”号的数,0既不是正数也不是负数;由此可知,这个数是十位上的数是0,这个数是201,据此解答。
【详解】根据分析可知,一个三位数(各个数位上的数字不相同),百位上的数字既是质数又是偶数,个位上的数字既不是质数也不是合数,十位上的数字既不是正数又不负数。则这个数是201。
【点睛】熟练掌握质数、合数、奇数、偶数、正数、负数的意义是解答本题的关键。
15.30
【分析】2的倍数特点:个位上是0、2、4、6、8,5的倍数特点:个位上是0或5,3的倍数特点:各个数位上数字之和是3的倍数,根据2、3、5的倍数特征可知,同时是2、3、5的倍数,个位上的数字是0,各个数位上的数字的和是3的倍数,据此解答即可。
【详解】同时是2、3和5的倍数的最小两位自然数是30。
【点睛】本题主要考查2、3、5的倍数特征,注意个位是0的数同时是2和5的倍数,3的倍数特征是:各个数位上的和是3的倍数,这个数就是3的倍数。
16.4
【分析】由于每行的人数×每列的人数=总人数,先找出72的因数,可以一对一对的找,进而根据题意确定可能每行排的人数和排的列数。
【详解】72的因数有:1,2,3,4,6,8,9,12,18,24,36,72。
因为每列或每行不少于3人,且每行的人数要比每列的人数少,因此符合这些条件的因数有:3,4,5,8,9,12,18,24。
每列24人,排3行;
每列18人,排4行;
每列12人,排6行;
每列9人,排8行。
一共有4种排法。
某表演队72人需要安排队列,要求每列或每行不少于3人且每行的人数要比每列的人数少,那么有4种排法。
【点睛】熟练掌握求一个数的因数的方法是解答本题的关键。
17.×
【分析】一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。根据求一个数的因数的方法求出12的因数;再根据质数的意义,一个自然数如果只有1和它本身两个因数,这样的数叫做质数。据此解答即可。
【详解】12的因数有1、2、3、4、6、12。
在这些因数中质数有2和3两个。
因此题干中的结论是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握求一个数的因数的方法及应用,质数的意义及应用。
18.×
【分析】找一个因数的方法:把一个因数写出两个整数相乘的形式,这两个整数就是这个数的因数,根据此方法即可找出这个数的所有因数。
【详解】由分析可知:
找因数是通过乘法进行寻找,原题说法错误。
故答案为:×
【点睛】本题主要考查找因数的方法,学会找因数的方法并灵活运用。
19.√
【分析】求一个数倍数的方法:用这个数分别乘自然数:1、2、3、4、5、……,就得到这个数的1倍、2倍、3倍、4倍、5倍、……据此求出100以内15的所有倍数即可。
【详解】15×1=15
15×2=30
15×3=45
15×4=60
15×5=75
15×6=90
15×7=105
100以内15的倍数有:15、30、45、60、75、90,共有6个。
故答案为:√
【点睛】列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。
20.×
【分析】根据合数的意义:除了1和它本身还有别的因数的数是合数;据此解答。
【详解】如3个连续的自然数:8、9、10(答案不唯一),都是合数;3个连续的自然数有可能都是合数。
原题干说法错误。
故答案为:×
【点睛】熟练掌握合数的意义是解答本题的关键。
21.见详解
【分析】根据质数与合数的意义,在自然数中,除了1和它本身外,没有别的因数的数为质数;除了1和它本身,还有别的因数的数为合数,据此解答。
【详解】
【点睛】本题考查质数与合数的意义,根据质数与合数的意义进行解答。
22.
【解析】略
23.这个六位数是920042
【分析】根据题意,逐一判断出每个数位上的数字各是多少,然后求出这个六位数是多少即可。
【详解】因为个位上是最小的质数
所以个位上是2
因为十位上是最小的合数
所以十位上是4
因为万位上的数既是质数又是偶数
所以万位上是2
因为十万位上的数是一位数中最大的自然数
所以十万位上是9
所以这个六位数是920042。
答:这个六位数是920042。
【点睛】(1)此题主要考查了整数的读法和写法,要熟练掌握,解答此题的关键是逐一判断出每个数位上的数字各是多少;
(2)此题还考查了奇数、偶数的特征,以及质数和合数的特征,要熟练掌握。
24.42人;11只
【分析】因为每人折纸鹤的只数乘这个班师生人数,可得一共折了多少只纸鹤,可得每人折纸鹤的只数和这个班师生人数都是473的因数,找出473的因数。再根据实际情况合理选定师生人数,最后再从师生人数中减去李老师1个人的人数即得这个班的学生人数。
【详解】473=11×43
根据实际情况可得学生有43―1=42(人)
答:这个班有学生42人,每人折纸鹤11只。
【点睛】本题主要考查了找一个数的因数的方法,关键是找出473的因数。
25.7号和13号
【分析】只有1和它本身两个因数的数叫做质数,据此分别写出和是20的两个数,再进行判断。
【详解】
在这几组加数中,只有3、17与7、13这两组数都是质数,又因为差不超过10,所以只有7、13符合题意。
答:他们的座位号分别是7号和13号。
【点睛】本题考查质数的应用。根据质数的意义找出符合题意的数是解题的关键。
26.2行、4行、8行、16行;4种
【分析】把32名同学平均分成若干行,那么行数和每行的人数相乘的积是32,根据找因数的方法,可以一对一的找,有多少个因数就有多少种排法,再结合题目进行分析即可。
【详解】由分析可得:
32=1×32,即每行1人,排32行,不符合题意;或者每行32人,排1行,不符合题意。
32=2×16,即每行2人,排16行;或每行16人,排2行;
32=4×8,即每行4人,排8行;或每行8人,排4行;
答:可以排2行、4行、8行、16行。共有4种排法。
【点睛】本题考查了找一个数因数的方法,解答此题的关键是把32分解因数,再对分解出来的因数结合题目进行分析,看是否需要排除。
27.如果每2个包装成一袋,不能正好包完;如果每5个包装成一袋,能正好包完
【分析】根据2的倍数特征:个位上是0、2、4,6,8的数都是2的倍数;5的倍数特征:个位上的数是0或5的数,是5的倍数,用225除以2,如果没有余数,正好包完,如果有余数,不能正好包完;同样再用225÷5,如果没有余数,正好包完,如果有余数,不能正好包完;据此解答。
【详解】225÷2=112(袋)……1(个),225不是2的倍数,
如果每2个包装成一袋,不能正好包完。
225÷5=45(袋),225是5的倍数;
如果每5个包装成一袋,能正好包完。
答:如果每2个包装成一袋,不能正好包完;如果每5个包装成一袋,能正好包完。
【点睛】熟练掌握2的倍数特征和5的倍数特征是解答本题的关键。
28.每5个装一袋,不能正好装完;每2个装一袋,能正好装完
【分析】根据2的倍数特征:个位上是0、2、4,6,8的数都是2的倍数;5的倍数特征:个位上的数是0或5的数,是5的倍数,再根据能被2,5整除的数的特征进行判断是否正好整完。
【详解】64÷5=12(袋)……4(个),64不能被5整除,不是5的倍数,不能正好装完;
64÷2=32(袋),64能被2整数,是2的倍数,能装好装完。
答:每5个装一袋,不能正好装完,每2个装一袋,能正好装完。
【点睛】熟练掌握2、5的倍数特征是解答本题的关键。
29.422
【分析】一个数,除了1和它本身,还有其他因数的数,叫做合数,最小的合数是4;一个数,只要1和它本身两个因数,这样的数叫做质数,最小的质数是2,据此解答。
【详解】最小的合数是4,百位上的数是4;
4÷2=2;十位上的数是2;
最小的质数是2,个位上的数是2。
这个数是422。
答:这个三位数是422。
【点睛】熟练掌握质数和合数的意义是解答本题的关键。
30.见详解
【分析】根据题意,只要求出每箱装饮料的数量是80的因数,即可解答。
【详解】①4瓶装:80÷4=20(个),可以用每箱4瓶装的包装盒;需要20个包装盒;
②5瓶装:80÷5=16(个),可以用每箱5瓶装的包装盒;需要16个包装盒;
③10瓶装:80÷10=8(个),可以用每箱10瓶装的包装盒;需要8个包装盒;
④12瓶装:80÷12≈6.6(个),不可以用每箱12瓶装的包装盒。
表如下:
包装方式 4瓶 5瓶 10瓶
包装盒数量 20个 16个 8个
【点睛】熟练掌握因数与倍数的关键是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
