国庆节作业:第四章 图形的相似训练试卷(含答案)
文档属性
| 名称 | 国庆节作业:第四章 图形的相似训练试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-28 16:35:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
国庆节作业:《相似图形》训练试卷
选择题
1.下列各组中的四条线段成比例的是( )
A.1,1,2,3 B.1,2,3,4 C.2,3,4,5 D.2,3,6,9
2.若,则下列变形错误的是( )
A. B. C. D.
3.如图,,若,,,则等于( )
A.5 B.6 C.7 D.9
4.如图,已知,那么添加下列一个条件后,不能判定的是( )
A. B. C. D.
5.如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与相似的三角形是( )
A.B.C. D.
6.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上,
已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,
则树高AB =( )m.
A.3.5 B.4 C.4.5 D.5
7.如图,在中,,且,被、分成三部分,
且三部分面积分别为,,,则 )
A.1:1:1 B.1:2:3 C.1:3:5 D.1:4:9
8 . 图1是装了液体的高脚杯示意图(数据如图),
用去一部分液体后如图2所示,此时液面( )cm
A.1 B.2 C.3 D.4
如图,在中,,点D为线段上一动点(不与点B,C重合),
连接,作,交线段于点E.
下面是某学习小组根据题意得到的结论:
甲同学:;
乙同学:若,则;
丙同学:当时,D为的中点.
则下列说法正确的是( )
A.只有甲同学正确 B.乙和丙同学都正确
C.甲和丙同学正确 D.三个同学都正确
10 . 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,
延长EF交边AB于点G,连接DG、BF,给出下列结论:
①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
填空题(本大题共有6个小题,每小题3分,共18分)
1.如果,那么的值为 .
2.为了估计河的宽度,在河的对岸选定一个目标作为点A.再在河的这一边选定点B和C,
使,然后再选定点E,使,用视线确定与交于点D.
此时,测得,,,则两岸间的距离是 .
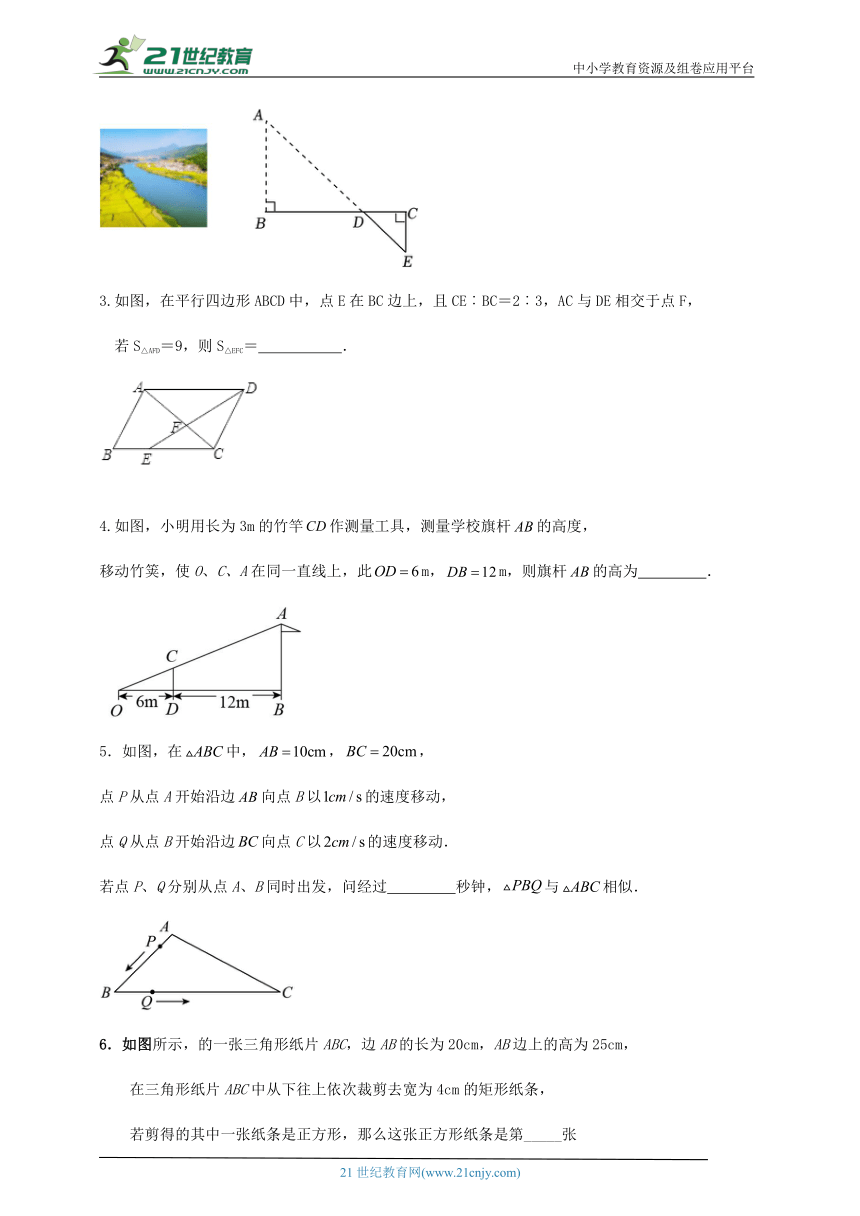
3.如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,
若S△AFD=9,则S△EFC= .
4.如图,小明用长为3m的竹竿作测量工具,测量学校旗杆的高度,
移动竹 ,使O、C、A在同一直线上,此m,m,则旗杆的高为 .
如图,在中,,,
点P从点A开始沿边向点B以的速度移动,
点Q从点B开始沿边向点C以的速度移动.
若点P、Q分别从点A、B同时出发,问经过 秒钟,与相似.
6.如图所示,的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,
在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,
若剪得的其中一张纸条是正方形,那么这张正方形纸条是第_____张
三、解答题
1.已知,且,求值.
2.如图, ,,,,求的长.
3.如图,,且,求证:.
4.在中,,,点是边上一点,
过点作,交于点,求证:.
5.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
6.如图所示,在等腰三角形ABC中,底边BC=60,高AD=40,四边形PQRS是正方形.
(1) △ASR与△ABC相似吗 为什么
(2)求正方形PQRS的边长.
7.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
8.如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm. P、Q分别为AB、BC上的动点,
点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,
移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
(1)当t为何值时,△BPQ与△ABC相似; (2)当t为何值时,△BPQ是等腰三角形.
9.【问题发现】
(1)如图1,在等腰直角中,点D是斜边上任意一点,在的右侧作等腰直角,
使,,连接,则和的数量关系为 ;
【拓展延伸】
如图2,在等腰中,,点D是边上任意一点(不与点B,C重合),
在的右侧作等腰,使,,
连接,则(1)中的结论是否仍然成立,并说明理由;
【归纳应用】
在(2)的条件下,若,,点D是射线上任意一点,
请直接写出当时的长.
国庆节作业:《相似图形》训练试卷 解答
选择题
1.下列各组中的四条线段成比例的是( )
A.1,1,2,3 B.1,2,3,4 C.2,3,4,5 D.2,3,6,9
【答案】D
2.若,则下列变形错误的是( )
A. B. C. D.
【答案】D
3.如图,,若,,,则等于( )
A.5 B.6 C.7 D.9
【答案】B
4.如图,已知,那么添加下列一个条件后,不能判定的是( )
A. B. C. D.
【答案】D
5.如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与相似的三角形是( )
A.B.C. D.
【答案】C
6.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上,
已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,
则树高AB =( )m.
A.3.5 B.4 C.4.5 D.5
【答案】D
7.如图,在中,,且,被、分成三部分,
且三部分面积分别为,,,则 )
A.1:1:1 B.1:2:3 C.1:3:5 D.1:4:9
【答案】C
8 . 图1是装了液体的高脚杯示意图(数据如图),
用去一部分液体后如图2所示,此时液面( )cm
A.1 B.2 C.3 D.4
【答案】C
9.如图,在中,,点D为线段上一动点(不与点B,C重合),
连接,作,交线段于点E.
下面是某学习小组根据题意得到的结论:
甲同学:;
乙同学:若,则;
丙同学:当时,D为的中点.
则下列说法正确的是( )
A.只有甲同学正确 B.乙和丙同学都正确
C.甲和丙同学正确 D.三个同学都正确
【答案】D
10 . 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,
延长EF交边AB于点G,连接DG、BF,给出下列结论:
①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【答案】C
填空题(本大题共有6个小题,每小题3分,共18分)
1.如果,那么的值为 .
【答案】
2.为了估计河的宽度,在河的对岸选定一个目标作为点A.再在河的这一边选定点B和C,
使,然后再选定点E,使,用视线确定与交于点D.
此时,测得,,,则两岸间的距离是 .
【答案】
3.如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,
若S△AFD=9,则S△EFC= .
【答案】4
4.如图,小明用长为3m的竹竿作测量工具,测量学校旗杆的高度,
移动竹 ,使O、C、A在同一直线上,此m,m,则旗杆的高为 .
【答案】9
5 .如图,在中,,,
点P从点A开始沿边向点B以的速度移动,
点Q从点B开始沿边向点C以的速度移动.
若点P、Q分别从点A、B同时出发,问经过 秒钟,与相似.
【答案】2或5
6.如图所示,的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,
在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,
若剪得的其中一张纸条是正方形,那么这张正方形纸条是第_____张
【答案】5
三、解答题
1.已知,且,求值.
解:设,
,,,
,
,
,
,
的值为.
2.如图, ,,,,求的长.
解:∵,,
∴;
∵,
∴,
即:;
∴的长为15.
3.如图,,且,求证:.
证明: ,
.
又,
,
即,
∴.
4.在中,,,点是边上一点,
过点作,交于点,求证:.
证明:如图所示:
,,
为等腰直角三角形,
,
,
,
,
,
,
.
5.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
解:(1)证明:∵AB=AC
∴∠B=∠C
∵∠ADC=∠B+∠BAD
∠ADC=∠ADE+∠CDE
∵∠ADE=∠B
∴∠BAD=∠CDE
∴△ABD∽△CDE
(2)∵AB=AC,AC=12
∴AB=12
由(1)知,△ABD∽△CDE
∴=
即=
∴BD=3或8
6.如图所示,在等腰三角形ABC中,底边BC=60,高AD=40,四边形PQRS是正方形.
(1) △ASR与△ABC相似吗 为什么
(2)求正方形PQRS的边长.
解:(1)∵四边形PQRS是正方形,
∴SR∥PQ,
∴∠ASR=∠ABC,∠ARS=∠ACB,
∴△ASR∽△ABC;
(2)设正方形的边长为x,则SR=x,SR=DE=x,AE=40﹣x,
∵△ASR∽△ABC,
∴AE:AD=SR:BC,
∵BC=60,AD=40,
∴(40﹣x):40=x:60,
∴x=24,
即正方形的边长为24.
7.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
解:(1)证明:如图所示:
∵四边形ABCD是平行四边形
∴∠B=∠ADC
∵∠AFE=∠B,∴∠AFE=∠ADC
∵∠AFE=∠1+∠2,∠ADC=∠3+∠2
∴∠1+∠2=∠3+∠2,即∠1=∠3
∴∠DAF=∠CDE
证明:∵四边形ABCD是平行四边形
∴AD∥BC,∴∠2=∠4
由(1)得∠1=∠3 ∴△ADF∽△DEC
∵AE⊥BC,∴AE⊥AD
∴DE=
由(2)可知:△ADF∽△DEC,CD=AB=7
∴ ∴
∴AF=
8.如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm. P、Q分别为AB、BC上的动点,
点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,
移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
(1)当t为何值时,△BPQ与△ABC相似; (2)当t为何值时,△BPQ是等腰三角形.
解:(1)∵在△ABC中,∠C=90°,AC=3cm,BC=4cm.
∴AB=(cm).
∵△BPQ和△ABC有公共角∠B,
∴①当时,△BPQ∽△BCA,
由此可得: ,
解得: ;
②当时,△BPQ∽△BAC,
由此可得: ,
解得: ;
∴当或时,△BPQ与△ABC相似;
①如图1,当BP=BQ时,△BPQ是等腰三角形,
由题意可得: ,解得: ;
②如图2,当BQ=PQ时,过点Q作QE⊥AB于点E,
则BE=PE=BP=,∠BEQ=∠C=90°,
又∵∠B=∠B,∴△BEQ∽△BCA,
∴,即 ,解得: ;
③如图3,当PB=PQ时,过点P作PE⊥BC于点E,
则BE=EQ= ,∠BEP=∠C=90°,
又∵∠B=∠B,∴△BEP∽△BCA,
∴,即,解得: ;
综上所述,当, , 时,△BPQ是等腰三角形.
9.【问题发现】
(1)如图1,在等腰直角中,点D是斜边上任意一点,在的右侧作等腰直角,
使,,连接,则和的数量关系为 ;
【拓展延伸】
如图2,在等腰中,,点D是边上任意一点(不与点B,C重合),
在的右侧作等腰,使,,
连接,则(1)中的结论是否仍然成立,并说明理由;
【归纳应用】
在(2)的条件下,若,,点D是射线上任意一点,
请直接写出当时的长.
解:(1)相等,∵和都是等腰直角三角形,
∴,
∴,
即,
∴,
∴,
故答案为:相等;
(2)成立,
理由:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴∠;
(3)当点D在线段上时,如图2,
由(2)知,,
∴,
∴,
∴.
当点D在线段的延长线上时,如图3,
∵,
∴,
∵,
∴,
∵,
∴,
∴∠BAD=∠CAE,
∵,,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
综上可知,的长为2或6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
国庆节作业:《相似图形》训练试卷
选择题
1.下列各组中的四条线段成比例的是( )
A.1,1,2,3 B.1,2,3,4 C.2,3,4,5 D.2,3,6,9
2.若,则下列变形错误的是( )
A. B. C. D.
3.如图,,若,,,则等于( )
A.5 B.6 C.7 D.9
4.如图,已知,那么添加下列一个条件后,不能判定的是( )
A. B. C. D.
5.如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与相似的三角形是( )
A.B.C. D.
6.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上,
已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,
则树高AB =( )m.
A.3.5 B.4 C.4.5 D.5
7.如图,在中,,且,被、分成三部分,
且三部分面积分别为,,,则 )
A.1:1:1 B.1:2:3 C.1:3:5 D.1:4:9
8 . 图1是装了液体的高脚杯示意图(数据如图),
用去一部分液体后如图2所示,此时液面( )cm
A.1 B.2 C.3 D.4
如图,在中,,点D为线段上一动点(不与点B,C重合),
连接,作,交线段于点E.
下面是某学习小组根据题意得到的结论:
甲同学:;
乙同学:若,则;
丙同学:当时,D为的中点.
则下列说法正确的是( )
A.只有甲同学正确 B.乙和丙同学都正确
C.甲和丙同学正确 D.三个同学都正确
10 . 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,
延长EF交边AB于点G,连接DG、BF,给出下列结论:
①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
填空题(本大题共有6个小题,每小题3分,共18分)
1.如果,那么的值为 .
2.为了估计河的宽度,在河的对岸选定一个目标作为点A.再在河的这一边选定点B和C,
使,然后再选定点E,使,用视线确定与交于点D.
此时,测得,,,则两岸间的距离是 .
3.如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,
若S△AFD=9,则S△EFC= .
4.如图,小明用长为3m的竹竿作测量工具,测量学校旗杆的高度,
移动竹 ,使O、C、A在同一直线上,此m,m,则旗杆的高为 .
如图,在中,,,
点P从点A开始沿边向点B以的速度移动,
点Q从点B开始沿边向点C以的速度移动.
若点P、Q分别从点A、B同时出发,问经过 秒钟,与相似.
6.如图所示,的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,
在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,
若剪得的其中一张纸条是正方形,那么这张正方形纸条是第_____张
三、解答题
1.已知,且,求值.
2.如图, ,,,,求的长.
3.如图,,且,求证:.
4.在中,,,点是边上一点,
过点作,交于点,求证:.
5.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
6.如图所示,在等腰三角形ABC中,底边BC=60,高AD=40,四边形PQRS是正方形.
(1) △ASR与△ABC相似吗 为什么
(2)求正方形PQRS的边长.
7.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
8.如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm. P、Q分别为AB、BC上的动点,
点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,
移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
(1)当t为何值时,△BPQ与△ABC相似; (2)当t为何值时,△BPQ是等腰三角形.
9.【问题发现】
(1)如图1,在等腰直角中,点D是斜边上任意一点,在的右侧作等腰直角,
使,,连接,则和的数量关系为 ;
【拓展延伸】
如图2,在等腰中,,点D是边上任意一点(不与点B,C重合),
在的右侧作等腰,使,,
连接,则(1)中的结论是否仍然成立,并说明理由;
【归纳应用】
在(2)的条件下,若,,点D是射线上任意一点,
请直接写出当时的长.
国庆节作业:《相似图形》训练试卷 解答
选择题
1.下列各组中的四条线段成比例的是( )
A.1,1,2,3 B.1,2,3,4 C.2,3,4,5 D.2,3,6,9
【答案】D
2.若,则下列变形错误的是( )
A. B. C. D.
【答案】D
3.如图,,若,,,则等于( )
A.5 B.6 C.7 D.9
【答案】B
4.如图,已知,那么添加下列一个条件后,不能判定的是( )
A. B. C. D.
【答案】D
5.如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与相似的三角形是( )
A.B.C. D.
【答案】C
6.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上,
已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,
则树高AB =( )m.
A.3.5 B.4 C.4.5 D.5
【答案】D
7.如图,在中,,且,被、分成三部分,
且三部分面积分别为,,,则 )
A.1:1:1 B.1:2:3 C.1:3:5 D.1:4:9
【答案】C
8 . 图1是装了液体的高脚杯示意图(数据如图),
用去一部分液体后如图2所示,此时液面( )cm
A.1 B.2 C.3 D.4
【答案】C
9.如图,在中,,点D为线段上一动点(不与点B,C重合),
连接,作,交线段于点E.
下面是某学习小组根据题意得到的结论:
甲同学:;
乙同学:若,则;
丙同学:当时,D为的中点.
则下列说法正确的是( )
A.只有甲同学正确 B.乙和丙同学都正确
C.甲和丙同学正确 D.三个同学都正确
【答案】D
10 . 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,
延长EF交边AB于点G,连接DG、BF,给出下列结论:
①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【答案】C
填空题(本大题共有6个小题,每小题3分,共18分)
1.如果,那么的值为 .
【答案】
2.为了估计河的宽度,在河的对岸选定一个目标作为点A.再在河的这一边选定点B和C,
使,然后再选定点E,使,用视线确定与交于点D.
此时,测得,,,则两岸间的距离是 .
【答案】
3.如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,
若S△AFD=9,则S△EFC= .
【答案】4
4.如图,小明用长为3m的竹竿作测量工具,测量学校旗杆的高度,
移动竹 ,使O、C、A在同一直线上,此m,m,则旗杆的高为 .
【答案】9
5 .如图,在中,,,
点P从点A开始沿边向点B以的速度移动,
点Q从点B开始沿边向点C以的速度移动.
若点P、Q分别从点A、B同时出发,问经过 秒钟,与相似.
【答案】2或5
6.如图所示,的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,
在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,
若剪得的其中一张纸条是正方形,那么这张正方形纸条是第_____张
【答案】5
三、解答题
1.已知,且,求值.
解:设,
,,,
,
,
,
,
的值为.
2.如图, ,,,,求的长.
解:∵,,
∴;
∵,
∴,
即:;
∴的长为15.
3.如图,,且,求证:.
证明: ,
.
又,
,
即,
∴.
4.在中,,,点是边上一点,
过点作,交于点,求证:.
证明:如图所示:
,,
为等腰直角三角形,
,
,
,
,
,
,
.
5.如图,在△ABC中,AB=AC,D为BC边上一点,E为AC边上一点,且∠ADE=∠B.
(1)求证:△ABD∽△DCE;
(2)若AC=12,BC=11,CE=2,求BD的长.
解:(1)证明:∵AB=AC
∴∠B=∠C
∵∠ADC=∠B+∠BAD
∠ADC=∠ADE+∠CDE
∵∠ADE=∠B
∴∠BAD=∠CDE
∴△ABD∽△CDE
(2)∵AB=AC,AC=12
∴AB=12
由(1)知,△ABD∽△CDE
∴=
即=
∴BD=3或8
6.如图所示,在等腰三角形ABC中,底边BC=60,高AD=40,四边形PQRS是正方形.
(1) △ASR与△ABC相似吗 为什么
(2)求正方形PQRS的边长.
解:(1)∵四边形PQRS是正方形,
∴SR∥PQ,
∴∠ASR=∠ABC,∠ARS=∠ACB,
∴△ASR∽△ABC;
(2)设正方形的边长为x,则SR=x,SR=DE=x,AE=40﹣x,
∵△ASR∽△ABC,
∴AE:AD=SR:BC,
∵BC=60,AD=40,
∴(40﹣x):40=x:60,
∴x=24,
即正方形的边长为24.
7.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
解:(1)证明:如图所示:
∵四边形ABCD是平行四边形
∴∠B=∠ADC
∵∠AFE=∠B,∴∠AFE=∠ADC
∵∠AFE=∠1+∠2,∠ADC=∠3+∠2
∴∠1+∠2=∠3+∠2,即∠1=∠3
∴∠DAF=∠CDE
证明:∵四边形ABCD是平行四边形
∴AD∥BC,∴∠2=∠4
由(1)得∠1=∠3 ∴△ADF∽△DEC
∵AE⊥BC,∴AE⊥AD
∴DE=
由(2)可知:△ADF∽△DEC,CD=AB=7
∴ ∴
∴AF=
8.如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm. P、Q分别为AB、BC上的动点,
点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,
移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
(1)当t为何值时,△BPQ与△ABC相似; (2)当t为何值时,△BPQ是等腰三角形.
解:(1)∵在△ABC中,∠C=90°,AC=3cm,BC=4cm.
∴AB=(cm).
∵△BPQ和△ABC有公共角∠B,
∴①当时,△BPQ∽△BCA,
由此可得: ,
解得: ;
②当时,△BPQ∽△BAC,
由此可得: ,
解得: ;
∴当或时,△BPQ与△ABC相似;
①如图1,当BP=BQ时,△BPQ是等腰三角形,
由题意可得: ,解得: ;
②如图2,当BQ=PQ时,过点Q作QE⊥AB于点E,
则BE=PE=BP=,∠BEQ=∠C=90°,
又∵∠B=∠B,∴△BEQ∽△BCA,
∴,即 ,解得: ;
③如图3,当PB=PQ时,过点P作PE⊥BC于点E,
则BE=EQ= ,∠BEP=∠C=90°,
又∵∠B=∠B,∴△BEP∽△BCA,
∴,即,解得: ;
综上所述,当, , 时,△BPQ是等腰三角形.
9.【问题发现】
(1)如图1,在等腰直角中,点D是斜边上任意一点,在的右侧作等腰直角,
使,,连接,则和的数量关系为 ;
【拓展延伸】
如图2,在等腰中,,点D是边上任意一点(不与点B,C重合),
在的右侧作等腰,使,,
连接,则(1)中的结论是否仍然成立,并说明理由;
【归纳应用】
在(2)的条件下,若,,点D是射线上任意一点,
请直接写出当时的长.
解:(1)相等,∵和都是等腰直角三角形,
∴,
∴,
即,
∴,
∴,
故答案为:相等;
(2)成立,
理由:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴∠;
(3)当点D在线段上时,如图2,
由(2)知,,
∴,
∴,
∴.
当点D在线段的延长线上时,如图3,
∵,
∴,
∵,
∴,
∵,
∴,
∴∠BAD=∠CAE,
∵,,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
综上可知,的长为2或6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
