第十一章 三角形单元测试卷(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年八年级数学上册《第11章 三角形》单元测试卷(人教版)
一、选择题(每小题4分,满分40分)
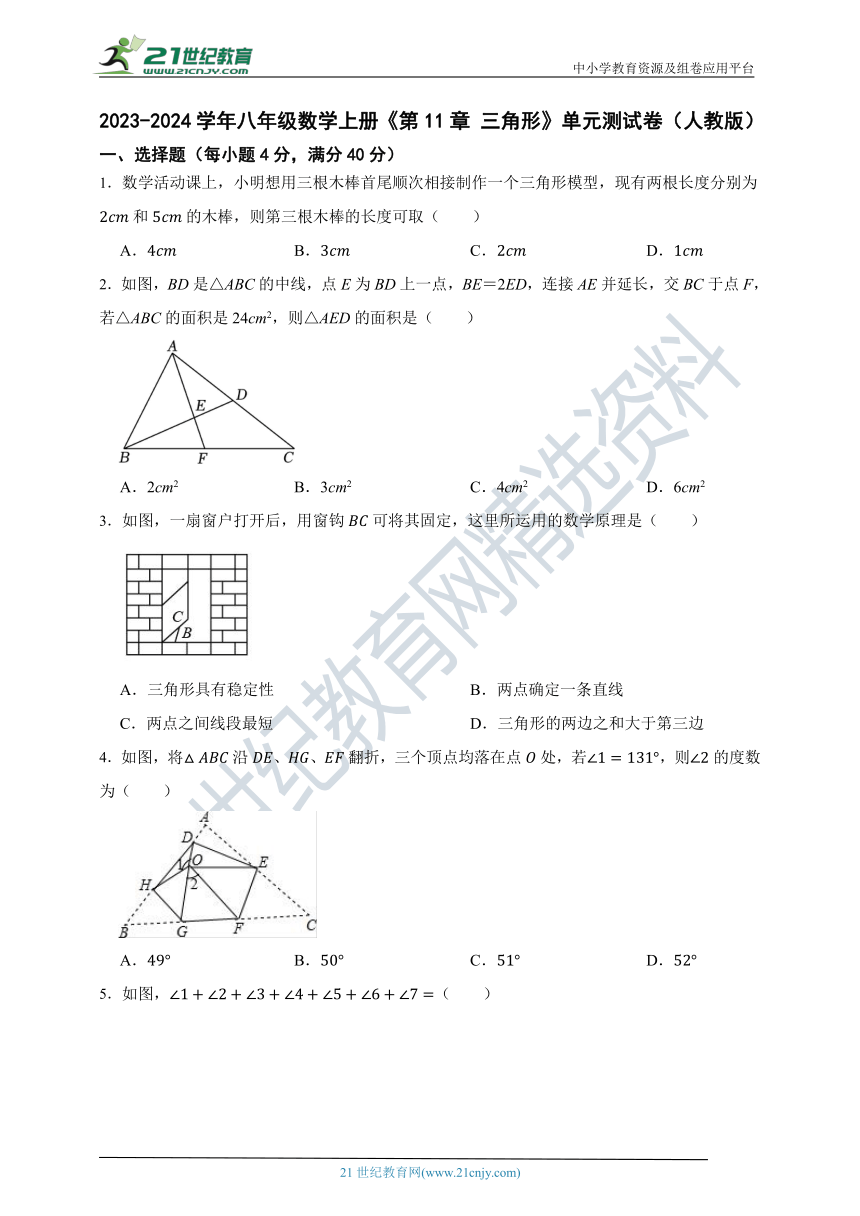
1.数学活动课上,小明想用三根木棒首尾顺次相接制作一个三角形模型,现有两根长度分别为和的木棒,则第三根木棒的长度可取( )
A. B. C. D.
2.如图,BD是△ABC的中线,点E为BD上一点,BE=2ED,连接AE并延长,交BC于点F,若△ABC的面积是24cm2,则△AED的面积是( )
A.2cm2 B.3cm2 C.4cm2 D.6cm2
3.如图,一扇窗户打开后,用窗钩可将其固定,这里所运用的数学原理是( )
A.三角形具有稳定性 B.两点确定一条直线
C.两点之间线段最短 D.三角形的两边之和大于第三边
4.如图,将沿、、翻折,三个顶点均落在点处,若,则的度数为( )
A. B. C. D.
5.如图,( )
A.480 B.500° C.540° D.600°
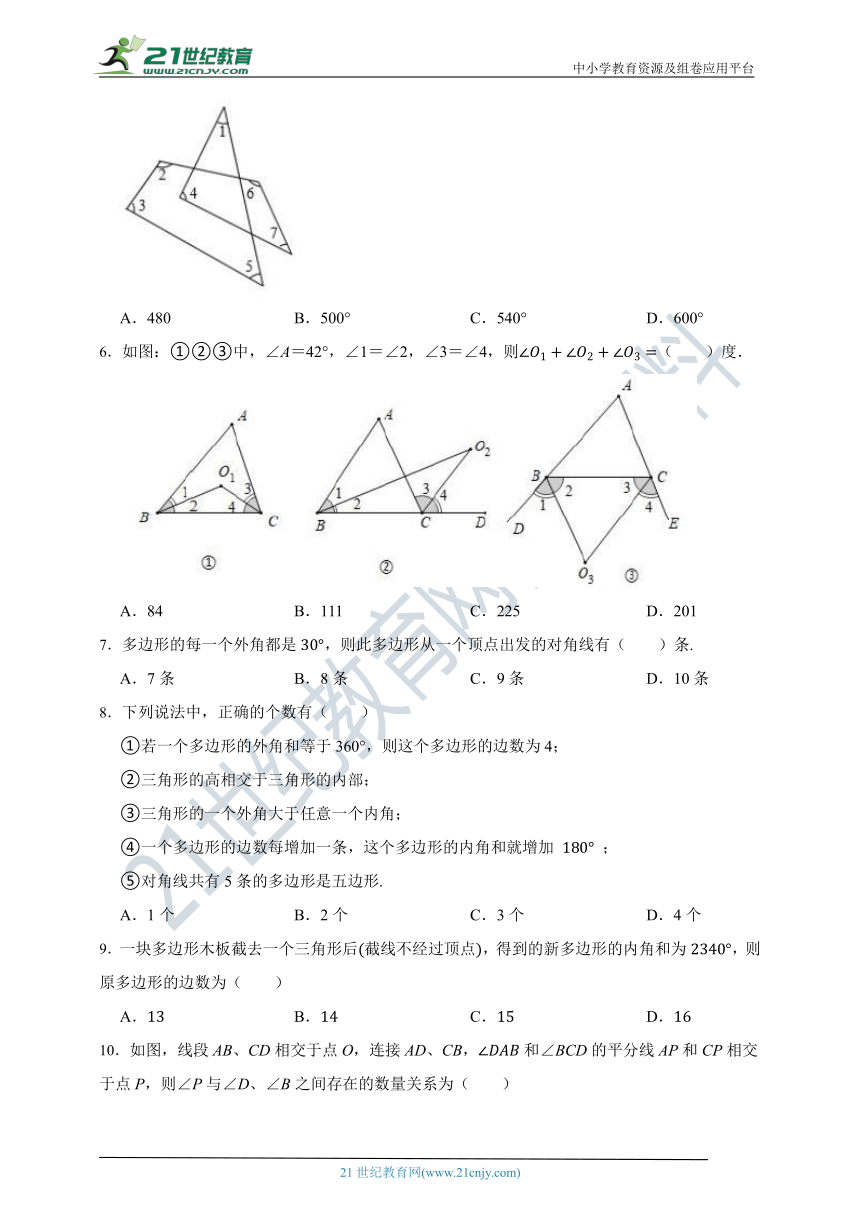
6.如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则( )度.
A.84 B.111 C.225 D.201
7.多边形的每一个外角都是,则此多边形从一个顶点出发的对角线有( )条.
A.7条 B.8条 C.9条 D.10条
8.下列说法中,正确的个数有( )
①若一个多边形的外角和等于360°,则这个多边形的边数为4;
②三角形的高相交于三角形的内部;
③三角形的一个外角大于任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加 ;
⑤对角线共有5条的多边形是五边形.
A.1个 B.2个 C.3个 D.4个
9.一块多边形木板截去一个三角形后截线不经过顶点,得到的新多边形的内角和为,则原多边形的边数为( )
A. B. C. D.
10.如图,线段AB、CD相交于点O,连接AD、CB,和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A. B.
C. D.
二、填空题(每小题5分,满分20分)
11.如图,将一副三角板的两个直角重合,使点在上,点在上,已知,,则的度数是 .
12.根据如图所表示的已知角的度数,求出其中的度数为 .
13.如图,△ABC中,E为BC边上一点,,点D为AC的中点,连接DE、AE,取DE的中点F,连接AF,若四边形ABEF的面积是6,则△ABC的面积是 .
14.探究与发现:如图,在中,,点D在边上,点E在边上,且,连接.
(1)当时,求 .
(2)当点D在(点除外)边上运动时,试猜想与的数量关系为 .
三、解答题(满分90分)
15.(8分)已知从m边形的一个顶点出发可以画4条对角线;从n边形的一个顶点出发的所有对角线把n边形分成6个三角形.求的值.
16.(8分)已知三角形的三边长分别为a,b,c,化简:.
17.(8分)如图,在中,是的角平分线,是边上的高,相交于点O,如果,求的度数.
18.(8分)如图,中,BE为AC边上的高,CD平分,CD、BE相交于点F.若,,求的度数.
19.(10分)如图,在△ABC中,∠ACB=90°,CA=CB.点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于点D,且∠CDE=60°,求∠DCE的度数.
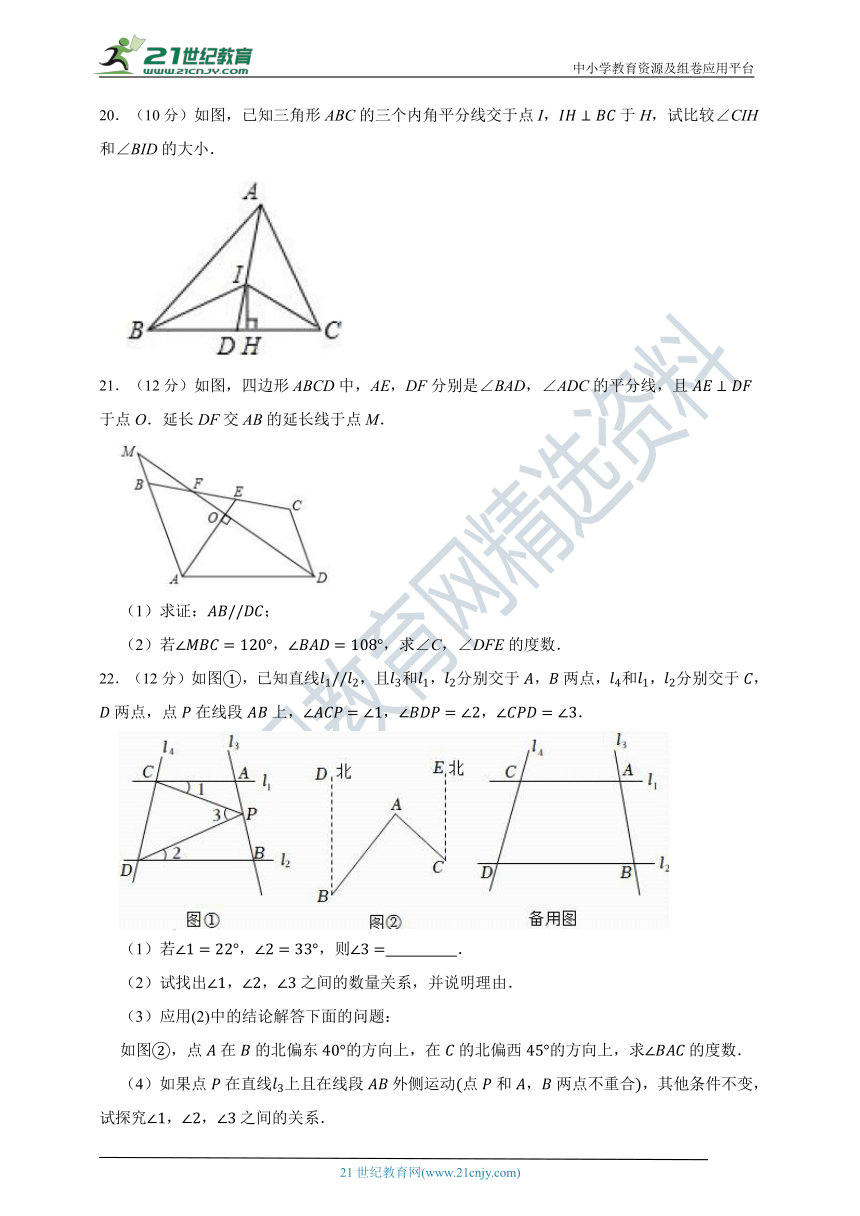
20.(10分)如图,已知三角形ABC的三个内角平分线交于点I,于H,试比较∠CIH和∠BID的大小.
21.(12分)如图,四边形ABCD中,AE,DF分别是∠BAD,∠ADC的平分线,且于点O.延长DF交AB的延长线于点M.
(1)求证:;
(2)若,,求∠C,∠DFE的度数.
22.(12分)如图,已知直线,且和,分别交于,两点,和,分别交于,两点,点在线段上,,,.
(1)若,,则 .
(2)试找出,,之间的数量关系,并说明理由.
(3)应用(2)中的结论解答下面的问题:
如图,点在的北偏东的方向上,在的北偏西的方向上,求的度数.
(4)如果点在直线上且在线段外侧运动点和,两点不重合,其他条件不变,试探究,,之间的关系.
23.(14分)(1)已知:如图1,P为△ADC内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,如果∠A=60°,那么∠P的度数;如果∠A=90°,那么∠P的度数;如果∠A=x°,则∠P的度数;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E的数量关系
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
(5)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:
答案解析部分
1.【答案】A
【知识点】三角形三边关系
【解析】【解答】解:∵三角形模型,现有两根长度分别为和的木棒,设第三边的长度为x,
∴第三边的长度取值范围为:.
∴长度的取值可能为4,5,6,
故答案为:A.
【分析】根据三角形的第三边大于两边之差,小于两边之和,即可求出第三边的取值范围,从而求出答案.
2.【答案】C
【知识点】三角形的角平分线、中线和高
【解析】【解答】解:∵BD是△ABC的中线,△ABC的面积是24cm2,
∴S△ABD=S△BCD=12,
∵BE=2ED,
∴S△AED=2S△AED,
∵S△AED+S△AED=S△ABD,
∴△AED的面积是4,
故答案为:C.
【分析】根据三角形的中线将三角形分成两个面积相等的三角形可得S△ABD=S△BCD=12,结合题意可得S△AED=2S△AED,即可求解.
3.【答案】A
【知识点】三角形的稳定性
【解析】【解答】解:一扇窗户打开后,用窗钩可将其固定,这里所运用的几何原理是三角形的稳定性,
故答案为:A.
【分析】利用三角形的稳定性求解即可。
4.【答案】A
【知识点】三角形内角和定理;翻折变换(折叠问题)
【解析】【解答】解:∵△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,
∴∠A=∠DOE,∠B=∠HOG,∠EOF=∠C,
∴∠DOE+∠HOG+∠EOF=∠A+∠B+∠C=180°,
∵∠DOE+∠HOG+∠EOF+∠1+∠2=360°,
∴∠2=360°-(∠DOE+∠HOG+∠EOF+∠1)=360°-(180°+131°)=49°.
故答案为:A.
【分析】由翻折可得∠A=∠DOE,∠B=∠HOG,∠EOF=∠C,从而根据三角形内角和定理可得∠DOE+∠HOG+∠EOF=180°,进而根据周角定义可算出∠2的度数.
5.【答案】C
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解。如图,连接AD,EF,AF、DE交于O。
∵∠AOD=∠EOF,
∴∠OAD+∠ODA=∠OEF+∠OFE,
在四边形ABCD中,∠BAD+∠B+∠C+∠ADC=360°,
∴∠OAD+∠2+∠3+∠5+∠1+∠ODA=360°,
∴∠2+∠3+∠5+∠1+∠OEF+∠OFE=360°,
在△EFG中,∠FEG+∠EFG+∠G=180°,
∴∠2+∠3+∠5+∠1+∠OEF+∠OFE+∠FEG+∠EFG+∠G=540°,
∴∠1+∠2+∠3+∠5+∠OEF+∠FEG+∠OFE+∠EFG+∠7=540°,
∴∠1+∠2+∠3+∠5+∠4+∠6+∠7=540°,
即∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
故答案为:C。
【分析】连接AD,EF,可以把这7个角,分别归纳在四边形ABCD和△EFG中,从而可求得它们的和为360°+180°=540°。
6.【答案】D
【知识点】三角形内角和定理;三角形的外角性质
【解析】【解答】
解:①
②
③∠O3=180°-(∠2+∠3);
∴∠O1+∠O2+∠O3=180°+21°=201°。
故答案为:D。
【分析】根据三角形内角和定理及三角形外角和内角的关系得:从而得出∠O1+∠O2+∠O3=201°。
7.【答案】C
【知识点】多边形的对角线;多边形内角与外角
【解析】【解答】解:∵多边形的每一个外角都是30°,
∵多边形的外角和为360°,
∴此多边形的边数为:,
∴从一个顶点出发的对角线共有(条).
故答案为:C.
【分析】由于任何多边形的外角和都是360°,故用360°除以每一个外角的度数即可得出多边形的边数,进而根据过n边形一个顶点可引(n-3)条对角线即可得出答案.
8.【答案】B
【知识点】三角形的角平分线、中线和高;三角形的外角性质;多边形的对角线;多边形内角与外角
【解析】【解答】解:①任意多边形的外角和等于360°,故原说法错误,不符合题意;
②只有锐角三角形的高相交于三角形的内部,故原说法错误,不符合题意;
③根据三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和,得三角形的一个外角大于任意一个于它不相邻的内角,故原说法错误,不符合题意;
④根据多边形内角和公式: ,得一个多边形的边数每增加一条,这个多边形的内角和就增加180°,故原说法正确,符合题意;
⑤n边形的对角线条数为: ,当n=5时, ,故原说法正确,符合题意;
综上,正确个数有2个.
故答案为:B.
【分析】任意多边形的外角和等于360°,据此判断①;只有锐角三角形的高相交于三角形的内部,据此判断②;根据外角的性质可判断③;根据多边形的内角和公式可判断④;n边形的对角线条数为: ,然后令n=5,求出对应的值,据此判断⑤.
9.【答案】B
【知识点】多边形内角与外角
【解析】【解答】解:设原多边形为n边形,
又由题知截线不经过顶点,
∴原n边形被截后所得的新多边形的边数为(n+1),
则(n+1-2)·180°=2340°,
解得n=14;
故答案为:B.
【分析】可设原多边形为n边形,又由题知截线不经过顶点,所以原n边形被截后所得的新多边形的边数为(n+1),再根据多边形内角和公式(n-2)·180°列方程解出n即可即.
10.【答案】B
【知识点】三角形内角和定理;三角形的外角性质;对顶角及其性质;角平分线的定义
【解析】【解答】解:在△AOD中:∠D=180°-∠DAO-∠AOD,
在△BOC中:∠B=180°-∠BCO-∠BOC,
∴∠B+∠D=180°-∠DAO-∠AOD+180°-∠BCO-∠BOC=360°-∠DAO-∠BCO-∠AOD-∠BOC,
∵AP、CP分别平分∠DAB和∠BCD,
∴∠DAO=2∠PAO,∠BCO=2∠PCO,
又∠AOD=∠BOC,
∴∠B+∠D=360°-2∠PAO-2∠PCO-2∠AOD=2(180°-∠PAO-∠PCO-∠AOD),
AP、CD的交点标为点E,
在△CPE中,
∠P=180°-∠PCO-∠CEP,
∵∠CEP=∠AOD+∠PAO,
∴∠P=180°-∠PCO-∠PAO-∠AOD,
∴∠P=(∠B+∠D)。
故答案为:B。
【分析】首先根据三角形内角和定理分别得出∠B=180°-∠BCO-∠BOC,∠D=180°-∠DAO-∠AOD,再根据角平分线的定义和对顶角的性质得出∠B+∠D=2(180°-∠PAO-∠PCO-∠AOD),然后在△CPE中,得出∠P=180°-∠PCO-∠CEP,再根据三角形外角的性质,得出∠P=180°-∠PCO-∠PAO-∠AOD,从而得出结论∠P=(∠B+∠D)。
11.【答案】165°
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解:∵△ABC中,∠A=45°,∠C=90°,
∴∠ABC=45°,
∵△DEC中,∠E=30°,∠C=90°,
∴∠EDC=60°,
∴∠BFD=360°-∠ABC-∠C-∠EDC=360°-45°-60°-90°=165°.
故答案为:165°.
【分析】先根据三角形的内角和定理算出∠ABC与∠EDC的度数,进而根据四边形的内角和定理算出∠BFD的度数.
12.【答案】50°
【知识点】多边形内角与外角
【解析】【解答】解:图中角的外角为,
,
故答案为:50°.
【分析】利用多边形外角和求解即可。
13.【答案】12
【知识点】三角形的面积;线段的中点
【解析】【解答】解:∵CE=2BE,
∴S△ACE=2S△ABE,
∵点D是AC的中点,
∴S△ACE=2S△DCE,
∴S△ABE=S△DCE,
∵点F是DE的中点,
∴S△AEF=S△ADF,
∴S△ABE+S△AEF=S△DCE+S△ADF=,
即S四边形ABEF=,
∴=2S四边形ABEF=2×6=12.
故第1空答案为:12。
【分析】首先得出△ACE的面积等于△ABE面积的2倍,△ACE的面积也等于△CDE面积的2倍,故而得出△ABE的面积等于△CDE的面积;又根据点F是中点,可得出△AEF的面积等于△ADF的面积,从而得出△ABC的面积是四边形ABEF面积的2倍,即可得出答案。
14.【答案】(1)30°
(2)
【知识点】角的运算;三角形的外角性质
【解析】【解答】解:(1)是的外角,
∴,,
∴,
∴;
(2),
理由如下:设,
∴,,
∴,
∴,
∴.
故答案为:,.
【分析】(1)先求出,,再利用角的运算可得;
(2)设,则,再求出,即可得到,从而得解。
15.【答案】解:∵从m边形的一个顶点出发可以画4条对角线;从n边形的一个顶点出发的所有对角线把n边形分成6个三角形.
∴m=4+3=7,n=6+2=8,
,
当m=7,n=8时,原式.
【知识点】多边形的对角线
【解析】【分析】根据多边形的对角线可求出m、n的值,再代入计算即可.
16.【答案】解:由题意得:,
,
,
,
,
.
【知识点】整式的加减运算;三角形三边关系
【解析】【分析】根据三角形三边的关系去掉绝对值,再合并同类项即可。
17.【答案】解:∵是边上的高,
∴.
∴.
∵是的角平分线,
∴.
∴.
【知识点】余角、补角及其性质;三角形的角平分线、中线和高;角平分线的定义
【解析】【分析】根据高线的概念可得∠AEB=90°,则∠OAE=90°-∠AOE=20°,由角平分线的概念可得∠BAC=2∠OAE=40°,然后根据∠ABE=90°-∠BAC进行计算.
18.【答案】解:在中,,,
,
平分,
,
为边上的高,
,
.
【知识点】角的运算;三角形的角平分线、中线和高
【解析】【分析】根据三角形的角平分线、中线和高,以及角的运算法则即可得出答案。
19.【答案】解:∵CA=CB,CE=CA,
∴BC=CE,∠CAE=∠CEA,
∵CD平分∠ACB交AE于D,且∠CDE=60°,
∴∠ACD=∠DCB=45°,∠DAC+∠ACD=∠EDC=60°,
∴∠DAC=∠CEA=15°,
∴∠ACE=150°,
∴∠BCE=60°,
∴∠DCE=∠BCD+∠BCE=105°.
【知识点】角的运算;角平分线的定义
【解析】【分析】先利用等腰三角形的性质得出BC=CE,∠CAE=∠CEA,在利用外角的性质得出∠BCE的度数,进而利用等边三角形的判定得出答案。
20.【答案】解:因为AI、BI、CI为三角形ABC的角平分线,
所以,
.
所以
.
所以.
又因为,,
,
,
所以.
所以和是相等的关系.
【知识点】三角形内角和定理;三角形的外角性质;角平分线的定义
【解析】【分析】首先根据角平分线的定义,可得=90°,得出:,再根据三角形外角的性质得出:,根据三角形内角和定理,得出,从而得出结论:∠BID=∠CIH。
21.【答案】(1)证明:∵AE,DF分别是∠BAD,∠ADC的平分线,
∴,,
∵,
∴.
∴,
∴,
∴;
(2)解:∵
∴.
∵,
∴∠C=120°,
∵∠BAD=108°,
∴∠ADC=72°,
∴
∴.
【知识点】平行线的判定与性质;三角形内角和定理;角平分线的定义
【解析】【分析】(1)根据三角形内角和定理,可求得 ,再根据角平分线的定义求得,然后根据平行线的判定定理即可得出AB∥DC;
(2)首先根据两直线平行,内错角相等,可求得∠C=120°;根据两直线平行,同旁内角互补,得出∠ADC=72°,再根据角平分线的定义得出∠CDF=36°,进一步根据三角形内角和定理求得∠DFE=180°-120°-36°=24°。
22.【答案】(1)55°
(2)解:,理由如下:
,
,
在中,,
.
(3)解:如图,过点作,则,
则;
(4)解:当点在的外侧时,如图,过作,交于,
,
,
,
,
,
,
,,,
;
当点在的外侧时,如图,过作,交于,
,
,
,
,
,
,
,,,
.
综上,或.
【知识点】平行线的判定与性质;三角形内角和定理
【解析】【解答】(1)解:, , ∵在中,, , ,, .
【分析】(1)根据平行线的性质推出,利用三角形的内角和定理和等量转化即可求出,从而求出度数;
(2)利用第(1)问的方法即可推出 ,,之间的数量关系 ;
(3)根据平行线的性质和等量转化即可求出度数;
(4)分情况讨论,当点在的外侧时,作,从而推出和,通过等量转化和 ,,即可求出,,之间的数量关系 ;当点在的外侧时,作,运用第一种情况相同的方法即可推出 ,,之间的数量关系 .
23.【答案】解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠ACD
=180°﹣(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+∠A,
∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+ )°;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B);
(3)五边形ABCDEF的内角和为:(5﹣2) 180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠EDC﹣∠BCD
=180°﹣(∠EDC+∠BCD)
=180°﹣(540°﹣∠A﹣∠B﹣∠E)
=(∠A+∠B+∠E)﹣90°,
即∠P=(∠A+∠B+∠E)﹣90°.
(4)六边形ABCDEF的内角和为:(6﹣2) 180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠EDC﹣∠BCD
=180°﹣(∠EDC+∠BCD)
=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F)
=(∠A+∠B+∠E+∠F)﹣180°,
即∠P=(∠A+∠B+∠E+∠F)﹣180°.
(5)同(1)可得,∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
故答案为:120,135,(90+);(∠A+∠B);∠P=(∠A+∠B+∠E)﹣90°;∠P=(∠A+∠B+∠E+∠F)﹣180°;,∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
【知识点】多边形内角与外角
【解析】【分析】(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;
(2)根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理(1)解答即可;
(3)根据五边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(4)根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(5)根据n边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年八年级数学上册《第11章 三角形》单元测试卷(人教版)
一、选择题(每小题4分,满分40分)
1.数学活动课上,小明想用三根木棒首尾顺次相接制作一个三角形模型,现有两根长度分别为和的木棒,则第三根木棒的长度可取( )
A. B. C. D.
2.如图,BD是△ABC的中线,点E为BD上一点,BE=2ED,连接AE并延长,交BC于点F,若△ABC的面积是24cm2,则△AED的面积是( )
A.2cm2 B.3cm2 C.4cm2 D.6cm2
3.如图,一扇窗户打开后,用窗钩可将其固定,这里所运用的数学原理是( )
A.三角形具有稳定性 B.两点确定一条直线
C.两点之间线段最短 D.三角形的两边之和大于第三边
4.如图,将沿、、翻折,三个顶点均落在点处,若,则的度数为( )
A. B. C. D.
5.如图,( )
A.480 B.500° C.540° D.600°
6.如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则( )度.
A.84 B.111 C.225 D.201
7.多边形的每一个外角都是,则此多边形从一个顶点出发的对角线有( )条.
A.7条 B.8条 C.9条 D.10条
8.下列说法中,正确的个数有( )
①若一个多边形的外角和等于360°,则这个多边形的边数为4;
②三角形的高相交于三角形的内部;
③三角形的一个外角大于任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加 ;
⑤对角线共有5条的多边形是五边形.
A.1个 B.2个 C.3个 D.4个
9.一块多边形木板截去一个三角形后截线不经过顶点,得到的新多边形的内角和为,则原多边形的边数为( )
A. B. C. D.
10.如图,线段AB、CD相交于点O,连接AD、CB,和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A. B.
C. D.
二、填空题(每小题5分,满分20分)
11.如图,将一副三角板的两个直角重合,使点在上,点在上,已知,,则的度数是 .
12.根据如图所表示的已知角的度数,求出其中的度数为 .
13.如图,△ABC中,E为BC边上一点,,点D为AC的中点,连接DE、AE,取DE的中点F,连接AF,若四边形ABEF的面积是6,则△ABC的面积是 .
14.探究与发现:如图,在中,,点D在边上,点E在边上,且,连接.
(1)当时,求 .
(2)当点D在(点除外)边上运动时,试猜想与的数量关系为 .
三、解答题(满分90分)
15.(8分)已知从m边形的一个顶点出发可以画4条对角线;从n边形的一个顶点出发的所有对角线把n边形分成6个三角形.求的值.
16.(8分)已知三角形的三边长分别为a,b,c,化简:.
17.(8分)如图,在中,是的角平分线,是边上的高,相交于点O,如果,求的度数.
18.(8分)如图,中,BE为AC边上的高,CD平分,CD、BE相交于点F.若,,求的度数.
19.(10分)如图,在△ABC中,∠ACB=90°,CA=CB.点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于点D,且∠CDE=60°,求∠DCE的度数.
20.(10分)如图,已知三角形ABC的三个内角平分线交于点I,于H,试比较∠CIH和∠BID的大小.
21.(12分)如图,四边形ABCD中,AE,DF分别是∠BAD,∠ADC的平分线,且于点O.延长DF交AB的延长线于点M.
(1)求证:;
(2)若,,求∠C,∠DFE的度数.
22.(12分)如图,已知直线,且和,分别交于,两点,和,分别交于,两点,点在线段上,,,.
(1)若,,则 .
(2)试找出,,之间的数量关系,并说明理由.
(3)应用(2)中的结论解答下面的问题:
如图,点在的北偏东的方向上,在的北偏西的方向上,求的度数.
(4)如果点在直线上且在线段外侧运动点和,两点不重合,其他条件不变,试探究,,之间的关系.
23.(14分)(1)已知:如图1,P为△ADC内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,如果∠A=60°,那么∠P的度数;如果∠A=90°,那么∠P的度数;如果∠A=x°,则∠P的度数;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E的数量关系
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
(5)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:
答案解析部分
1.【答案】A
【知识点】三角形三边关系
【解析】【解答】解:∵三角形模型,现有两根长度分别为和的木棒,设第三边的长度为x,
∴第三边的长度取值范围为:.
∴长度的取值可能为4,5,6,
故答案为:A.
【分析】根据三角形的第三边大于两边之差,小于两边之和,即可求出第三边的取值范围,从而求出答案.
2.【答案】C
【知识点】三角形的角平分线、中线和高
【解析】【解答】解:∵BD是△ABC的中线,△ABC的面积是24cm2,
∴S△ABD=S△BCD=12,
∵BE=2ED,
∴S△AED=2S△AED,
∵S△AED+S△AED=S△ABD,
∴△AED的面积是4,
故答案为:C.
【分析】根据三角形的中线将三角形分成两个面积相等的三角形可得S△ABD=S△BCD=12,结合题意可得S△AED=2S△AED,即可求解.
3.【答案】A
【知识点】三角形的稳定性
【解析】【解答】解:一扇窗户打开后,用窗钩可将其固定,这里所运用的几何原理是三角形的稳定性,
故答案为:A.
【分析】利用三角形的稳定性求解即可。
4.【答案】A
【知识点】三角形内角和定理;翻折变换(折叠问题)
【解析】【解答】解:∵△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,
∴∠A=∠DOE,∠B=∠HOG,∠EOF=∠C,
∴∠DOE+∠HOG+∠EOF=∠A+∠B+∠C=180°,
∵∠DOE+∠HOG+∠EOF+∠1+∠2=360°,
∴∠2=360°-(∠DOE+∠HOG+∠EOF+∠1)=360°-(180°+131°)=49°.
故答案为:A.
【分析】由翻折可得∠A=∠DOE,∠B=∠HOG,∠EOF=∠C,从而根据三角形内角和定理可得∠DOE+∠HOG+∠EOF=180°,进而根据周角定义可算出∠2的度数.
5.【答案】C
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解。如图,连接AD,EF,AF、DE交于O。
∵∠AOD=∠EOF,
∴∠OAD+∠ODA=∠OEF+∠OFE,
在四边形ABCD中,∠BAD+∠B+∠C+∠ADC=360°,
∴∠OAD+∠2+∠3+∠5+∠1+∠ODA=360°,
∴∠2+∠3+∠5+∠1+∠OEF+∠OFE=360°,
在△EFG中,∠FEG+∠EFG+∠G=180°,
∴∠2+∠3+∠5+∠1+∠OEF+∠OFE+∠FEG+∠EFG+∠G=540°,
∴∠1+∠2+∠3+∠5+∠OEF+∠FEG+∠OFE+∠EFG+∠7=540°,
∴∠1+∠2+∠3+∠5+∠4+∠6+∠7=540°,
即∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
故答案为:C。
【分析】连接AD,EF,可以把这7个角,分别归纳在四边形ABCD和△EFG中,从而可求得它们的和为360°+180°=540°。
6.【答案】D
【知识点】三角形内角和定理;三角形的外角性质
【解析】【解答】
解:①
②
③∠O3=180°-(∠2+∠3);
∴∠O1+∠O2+∠O3=180°+21°=201°。
故答案为:D。
【分析】根据三角形内角和定理及三角形外角和内角的关系得:从而得出∠O1+∠O2+∠O3=201°。
7.【答案】C
【知识点】多边形的对角线;多边形内角与外角
【解析】【解答】解:∵多边形的每一个外角都是30°,
∵多边形的外角和为360°,
∴此多边形的边数为:,
∴从一个顶点出发的对角线共有(条).
故答案为:C.
【分析】由于任何多边形的外角和都是360°,故用360°除以每一个外角的度数即可得出多边形的边数,进而根据过n边形一个顶点可引(n-3)条对角线即可得出答案.
8.【答案】B
【知识点】三角形的角平分线、中线和高;三角形的外角性质;多边形的对角线;多边形内角与外角
【解析】【解答】解:①任意多边形的外角和等于360°,故原说法错误,不符合题意;
②只有锐角三角形的高相交于三角形的内部,故原说法错误,不符合题意;
③根据三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和,得三角形的一个外角大于任意一个于它不相邻的内角,故原说法错误,不符合题意;
④根据多边形内角和公式: ,得一个多边形的边数每增加一条,这个多边形的内角和就增加180°,故原说法正确,符合题意;
⑤n边形的对角线条数为: ,当n=5时, ,故原说法正确,符合题意;
综上,正确个数有2个.
故答案为:B.
【分析】任意多边形的外角和等于360°,据此判断①;只有锐角三角形的高相交于三角形的内部,据此判断②;根据外角的性质可判断③;根据多边形的内角和公式可判断④;n边形的对角线条数为: ,然后令n=5,求出对应的值,据此判断⑤.
9.【答案】B
【知识点】多边形内角与外角
【解析】【解答】解:设原多边形为n边形,
又由题知截线不经过顶点,
∴原n边形被截后所得的新多边形的边数为(n+1),
则(n+1-2)·180°=2340°,
解得n=14;
故答案为:B.
【分析】可设原多边形为n边形,又由题知截线不经过顶点,所以原n边形被截后所得的新多边形的边数为(n+1),再根据多边形内角和公式(n-2)·180°列方程解出n即可即.
10.【答案】B
【知识点】三角形内角和定理;三角形的外角性质;对顶角及其性质;角平分线的定义
【解析】【解答】解:在△AOD中:∠D=180°-∠DAO-∠AOD,
在△BOC中:∠B=180°-∠BCO-∠BOC,
∴∠B+∠D=180°-∠DAO-∠AOD+180°-∠BCO-∠BOC=360°-∠DAO-∠BCO-∠AOD-∠BOC,
∵AP、CP分别平分∠DAB和∠BCD,
∴∠DAO=2∠PAO,∠BCO=2∠PCO,
又∠AOD=∠BOC,
∴∠B+∠D=360°-2∠PAO-2∠PCO-2∠AOD=2(180°-∠PAO-∠PCO-∠AOD),
AP、CD的交点标为点E,
在△CPE中,
∠P=180°-∠PCO-∠CEP,
∵∠CEP=∠AOD+∠PAO,
∴∠P=180°-∠PCO-∠PAO-∠AOD,
∴∠P=(∠B+∠D)。
故答案为:B。
【分析】首先根据三角形内角和定理分别得出∠B=180°-∠BCO-∠BOC,∠D=180°-∠DAO-∠AOD,再根据角平分线的定义和对顶角的性质得出∠B+∠D=2(180°-∠PAO-∠PCO-∠AOD),然后在△CPE中,得出∠P=180°-∠PCO-∠CEP,再根据三角形外角的性质,得出∠P=180°-∠PCO-∠PAO-∠AOD,从而得出结论∠P=(∠B+∠D)。
11.【答案】165°
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解:∵△ABC中,∠A=45°,∠C=90°,
∴∠ABC=45°,
∵△DEC中,∠E=30°,∠C=90°,
∴∠EDC=60°,
∴∠BFD=360°-∠ABC-∠C-∠EDC=360°-45°-60°-90°=165°.
故答案为:165°.
【分析】先根据三角形的内角和定理算出∠ABC与∠EDC的度数,进而根据四边形的内角和定理算出∠BFD的度数.
12.【答案】50°
【知识点】多边形内角与外角
【解析】【解答】解:图中角的外角为,
,
故答案为:50°.
【分析】利用多边形外角和求解即可。
13.【答案】12
【知识点】三角形的面积;线段的中点
【解析】【解答】解:∵CE=2BE,
∴S△ACE=2S△ABE,
∵点D是AC的中点,
∴S△ACE=2S△DCE,
∴S△ABE=S△DCE,
∵点F是DE的中点,
∴S△AEF=S△ADF,
∴S△ABE+S△AEF=S△DCE+S△ADF=,
即S四边形ABEF=,
∴=2S四边形ABEF=2×6=12.
故第1空答案为:12。
【分析】首先得出△ACE的面积等于△ABE面积的2倍,△ACE的面积也等于△CDE面积的2倍,故而得出△ABE的面积等于△CDE的面积;又根据点F是中点,可得出△AEF的面积等于△ADF的面积,从而得出△ABC的面积是四边形ABEF面积的2倍,即可得出答案。
14.【答案】(1)30°
(2)
【知识点】角的运算;三角形的外角性质
【解析】【解答】解:(1)是的外角,
∴,,
∴,
∴;
(2),
理由如下:设,
∴,,
∴,
∴,
∴.
故答案为:,.
【分析】(1)先求出,,再利用角的运算可得;
(2)设,则,再求出,即可得到,从而得解。
15.【答案】解:∵从m边形的一个顶点出发可以画4条对角线;从n边形的一个顶点出发的所有对角线把n边形分成6个三角形.
∴m=4+3=7,n=6+2=8,
,
当m=7,n=8时,原式.
【知识点】多边形的对角线
【解析】【分析】根据多边形的对角线可求出m、n的值,再代入计算即可.
16.【答案】解:由题意得:,
,
,
,
,
.
【知识点】整式的加减运算;三角形三边关系
【解析】【分析】根据三角形三边的关系去掉绝对值,再合并同类项即可。
17.【答案】解:∵是边上的高,
∴.
∴.
∵是的角平分线,
∴.
∴.
【知识点】余角、补角及其性质;三角形的角平分线、中线和高;角平分线的定义
【解析】【分析】根据高线的概念可得∠AEB=90°,则∠OAE=90°-∠AOE=20°,由角平分线的概念可得∠BAC=2∠OAE=40°,然后根据∠ABE=90°-∠BAC进行计算.
18.【答案】解:在中,,,
,
平分,
,
为边上的高,
,
.
【知识点】角的运算;三角形的角平分线、中线和高
【解析】【分析】根据三角形的角平分线、中线和高,以及角的运算法则即可得出答案。
19.【答案】解:∵CA=CB,CE=CA,
∴BC=CE,∠CAE=∠CEA,
∵CD平分∠ACB交AE于D,且∠CDE=60°,
∴∠ACD=∠DCB=45°,∠DAC+∠ACD=∠EDC=60°,
∴∠DAC=∠CEA=15°,
∴∠ACE=150°,
∴∠BCE=60°,
∴∠DCE=∠BCD+∠BCE=105°.
【知识点】角的运算;角平分线的定义
【解析】【分析】先利用等腰三角形的性质得出BC=CE,∠CAE=∠CEA,在利用外角的性质得出∠BCE的度数,进而利用等边三角形的判定得出答案。
20.【答案】解:因为AI、BI、CI为三角形ABC的角平分线,
所以,
.
所以
.
所以.
又因为,,
,
,
所以.
所以和是相等的关系.
【知识点】三角形内角和定理;三角形的外角性质;角平分线的定义
【解析】【分析】首先根据角平分线的定义,可得=90°,得出:,再根据三角形外角的性质得出:,根据三角形内角和定理,得出,从而得出结论:∠BID=∠CIH。
21.【答案】(1)证明:∵AE,DF分别是∠BAD,∠ADC的平分线,
∴,,
∵,
∴.
∴,
∴,
∴;
(2)解:∵
∴.
∵,
∴∠C=120°,
∵∠BAD=108°,
∴∠ADC=72°,
∴
∴.
【知识点】平行线的判定与性质;三角形内角和定理;角平分线的定义
【解析】【分析】(1)根据三角形内角和定理,可求得 ,再根据角平分线的定义求得,然后根据平行线的判定定理即可得出AB∥DC;
(2)首先根据两直线平行,内错角相等,可求得∠C=120°;根据两直线平行,同旁内角互补,得出∠ADC=72°,再根据角平分线的定义得出∠CDF=36°,进一步根据三角形内角和定理求得∠DFE=180°-120°-36°=24°。
22.【答案】(1)55°
(2)解:,理由如下:
,
,
在中,,
.
(3)解:如图,过点作,则,
则;
(4)解:当点在的外侧时,如图,过作,交于,
,
,
,
,
,
,
,,,
;
当点在的外侧时,如图,过作,交于,
,
,
,
,
,
,
,,,
.
综上,或.
【知识点】平行线的判定与性质;三角形内角和定理
【解析】【解答】(1)解:, , ∵在中,, , ,, .
【分析】(1)根据平行线的性质推出,利用三角形的内角和定理和等量转化即可求出,从而求出度数;
(2)利用第(1)问的方法即可推出 ,,之间的数量关系 ;
(3)根据平行线的性质和等量转化即可求出度数;
(4)分情况讨论,当点在的外侧时,作,从而推出和,通过等量转化和 ,,即可求出,,之间的数量关系 ;当点在的外侧时,作,运用第一种情况相同的方法即可推出 ,,之间的数量关系 .
23.【答案】解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠ACD
=180°﹣(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+∠A,
∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+ )°;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B);
(3)五边形ABCDEF的内角和为:(5﹣2) 180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠EDC﹣∠BCD
=180°﹣(∠EDC+∠BCD)
=180°﹣(540°﹣∠A﹣∠B﹣∠E)
=(∠A+∠B+∠E)﹣90°,
即∠P=(∠A+∠B+∠E)﹣90°.
(4)六边形ABCDEF的内角和为:(6﹣2) 180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠EDC﹣∠BCD
=180°﹣(∠EDC+∠BCD)
=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F)
=(∠A+∠B+∠E+∠F)﹣180°,
即∠P=(∠A+∠B+∠E+∠F)﹣180°.
(5)同(1)可得,∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
故答案为:120,135,(90+);(∠A+∠B);∠P=(∠A+∠B+∠E)﹣90°;∠P=(∠A+∠B+∠E+∠F)﹣180°;,∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
【知识点】多边形内角与外角
【解析】【分析】(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;
(2)根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理(1)解答即可;
(3)根据五边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(4)根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(5)根据n边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
