3.1.1一元一次方程课件
文档属性
| 名称 | 3.1.1一元一次方程课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 674.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-14 16:09:31 | ||
图片预览





文档简介
课件23张PPT。3.1.1一元一次方程等式方程我回顾,我思考1+2=3
5=7-2
3+b=2b+1
4+x=7
0.7x=1400
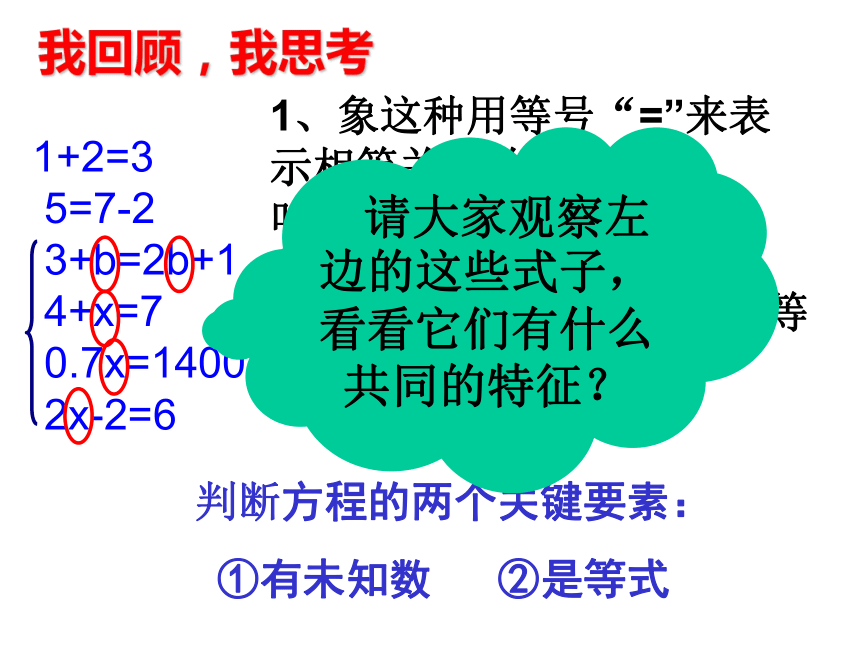
2x-2=61、象这种用等号“=”来表示相等关系的式子,叫 。2、象这样含有未知数的等式叫做 。判断方程的两个关键要素:
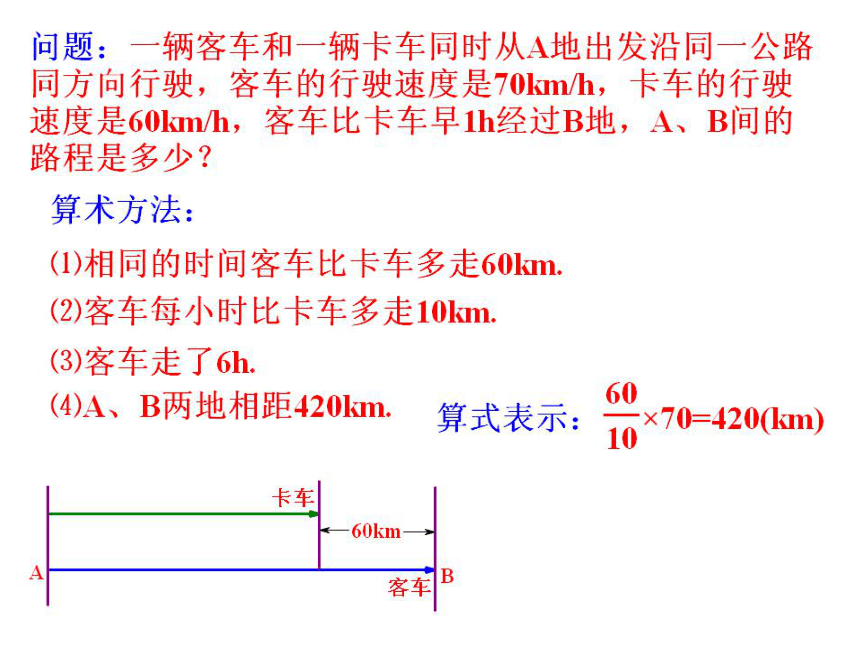
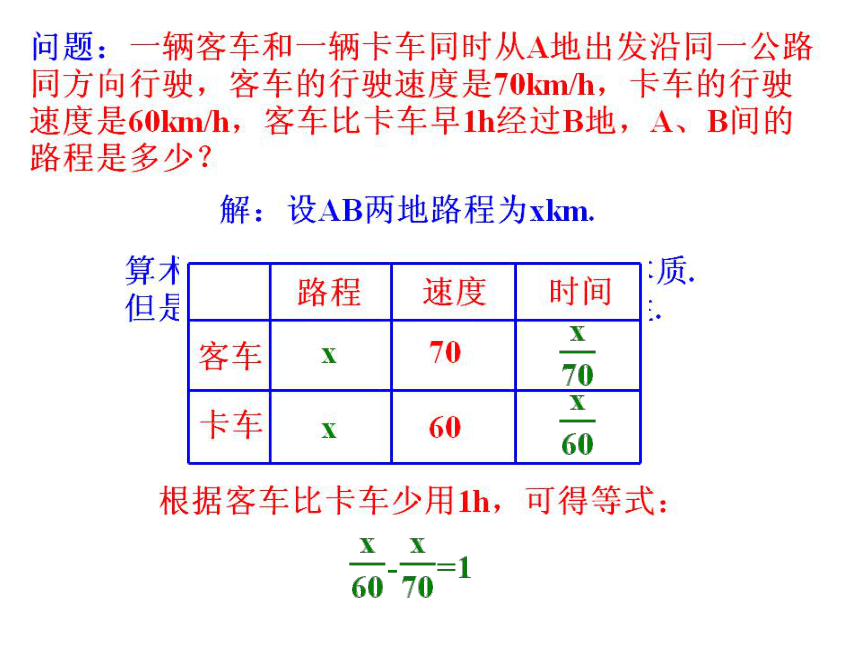
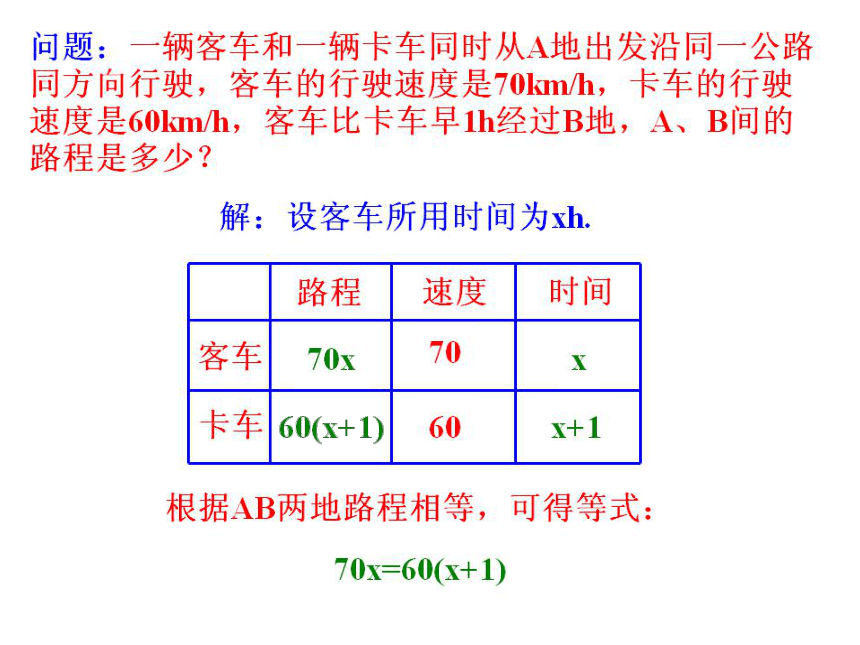
①有未知数 ②是等式 请大家观察左边的这些式子,看看它们有什么共同的特征?3、判断下列各式哪些是方程?√×√×√√√×我回顾,我思考①1+2=3 ( ) ②1+2x=4 ( )③x+y=2 ( ) ④x+1 ( )⑤x2-1=0 ( ) ⑥6a+8=3 ( )⑦ ( ) ⑧5x+2≥0 ( )讨论交流算术方法: 列出的算式表示解题的计算过程,其中只能 用已知数.对于较复杂的问题,列算式比较困难.
列方程(代数方法): 方程是根据题中的等量关系列出的等式.其中既含已知数,又含未未知数.使问题的已知量与未知量之间的关系很容易表示,解决问题就比较方便.所以,从算术到方程是数学的进步.根据下列问题,设未知数并列出方程:(1)用一根长为24cm的铁丝围成一个正方形,正方形的边长是多少?(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少个月,这台计算机的使用时间达到规定的检修时间2450?(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?我探究,我发现 4x=24,
1700+150x=2450,
0.52x-(1-0.52)x=80③等号两边都是整式;①都只含有一个未知数;②未知数的次数都是1;④都是方程。下面的三个方程:有什么共同点?我探究,我发现练习二:判断下列式子是不是一元一次
方程?
①2x+9=50 ( ) ②x+y=9 ( )
③3x2-4+x=0 ( ) ④6y+4=y+8 ( )
⑤2 +x=9 ( ) ⑥x+2 ( )
⑦ ( ) ⑧3x+x+1=5 ( )
小试身手注意:一元一次方程中,只含有一个未知数,且未知数的次数都是1,等号两边都是整式。√√×√××√×思考想一想:⑴使得方程4x=24成立的x的值为多少?当x=6时,方程4x=24成立。(2)使得方程5x+2=12成立的x的值为多少?当x=2时,方程5x+2=12成立。方程的解:使方程中等号左右两边相等的未知数的值叫方程的解。x=1和x=5哪一个是方程1700+150x=2450的解? 实践练习解:当x=1时 方程的左边=1700+150×1
=1700+150=1850方程的左边≠右边,所以x=1不是方程1700+150x=2450的解。当x=5时方程的左边=1700+150×5=2450方程的左边=右边,所以x=5是方程1700+150x=2450的解。1、方程(a+6)x2 +3x-8=7是关于x的一元一次方程,则a= _____。2、列方程:某数χ的相反数比它的 大1,求某数。 -63、一元一次方程2x-3=5的解是( )
A、4 B、5 C、6 D、7A我掌握,我巩固4、x=2是下列哪个方程的解? .
(1) 3x-1=2x+1
(2) 3x+1=2x-1
(3) 3x+2x-2=0
(4) x-2=0
(1)(4) 5、根据下列问题,设未知数,列出方程:(1)、环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?(2)、甲种铅笔每枝0.3元,乙种铅笔每枝0.6元,用9元钱买了两种铅笔共20枝,两种铅笔各买了多少枝?(3)、一个梯形的下底比上底多2㎝,高是5㎝,面积是40㎝2,求上底. 智力闯关,谁是英雄第一关 是一元一次方程,则k=_______第二关: 是一元一次方程,则k=______第三关 : 是一元一次方程,则k=__: 第四关: 是一元一次方程,则k =____21或-1-1-2一种方法——列方程解决实际问题的方法;
三个概念——方程、一元一次方程、方程
的解;我收获,我总结1、通过本节的学习你有什么收获? 2、在这部分学习中,你还有什么困难?感悟 1、在一卷公元前1600年左右遗留下来的古埃及草卷中, 记载着一些数学问题.其中一个翻译过来就是“啊哈,它的全部,它的七分之一, 其和等于19”.你能求出问题中的“它”吗?请你能根据题意列出方程.设 :“它”为x,列出方程: x+ =19挑战时刻百羊问题:
2、我国明代数学家程大为曾提出过这样一个有趣问题。有一个人赶着一群羊在前面走,另一个人牵着一头羊跟在后面。后面的人问赶羊的人说:“你这群羊有一百只吗?”赶羊的人回答:“我如果再得这么一群羊,再得这么一群羊的一半,又再得这群羊的四分之一,把你牵的羊也给我,我恰好有一百只。”请问这群羊有多少头? 解:设这群羊有x只, 可列出方程:
x+x+ + +1=100上有20头、 下有52足,问鸡兔各有多少?自主探索~~~鸡兔同笼 思 维 拓 宽请看一例 2004年夏季奥运会上,我国获得32枚金牌。其中跳水队获得6枚金牌,比射击队获得金牌数的2倍少2枚。射击队获得多少枚金牌?跳水队比射 击队的 2倍 少2
枚
6=2x-2如果设射击队获得的金牌数为x练一练(根据下列问题中的条件列出方程)设这件衣服的原价为x元,
可列出方程 。 练一练(根据下列问题中的条件列出方程)2008年北京奥运会
的足球分赛场---秦
皇岛市奥体中心体
育场,其足球场的
周长为344米,长和
宽之差为36米,这
个足球场的长与宽
分别是多少米?设这个足球场的宽为x米,则长
为(x+36)米,可列出方程
。
5=7-2
3+b=2b+1
4+x=7
0.7x=1400
2x-2=61、象这种用等号“=”来表示相等关系的式子,叫 。2、象这样含有未知数的等式叫做 。判断方程的两个关键要素:
①有未知数 ②是等式 请大家观察左边的这些式子,看看它们有什么共同的特征?3、判断下列各式哪些是方程?√×√×√√√×我回顾,我思考①1+2=3 ( ) ②1+2x=4 ( )③x+y=2 ( ) ④x+1 ( )⑤x2-1=0 ( ) ⑥6a+8=3 ( )⑦ ( ) ⑧5x+2≥0 ( )讨论交流算术方法: 列出的算式表示解题的计算过程,其中只能 用已知数.对于较复杂的问题,列算式比较困难.
列方程(代数方法): 方程是根据题中的等量关系列出的等式.其中既含已知数,又含未未知数.使问题的已知量与未知量之间的关系很容易表示,解决问题就比较方便.所以,从算术到方程是数学的进步.根据下列问题,设未知数并列出方程:(1)用一根长为24cm的铁丝围成一个正方形,正方形的边长是多少?(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少个月,这台计算机的使用时间达到规定的检修时间2450?(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?我探究,我发现 4x=24,
1700+150x=2450,
0.52x-(1-0.52)x=80③等号两边都是整式;①都只含有一个未知数;②未知数的次数都是1;④都是方程。下面的三个方程:有什么共同点?我探究,我发现练习二:判断下列式子是不是一元一次
方程?
①2x+9=50 ( ) ②x+y=9 ( )
③3x2-4+x=0 ( ) ④6y+4=y+8 ( )
⑤2 +x=9 ( ) ⑥x+2 ( )
⑦ ( ) ⑧3x+x+1=5 ( )
小试身手注意:一元一次方程中,只含有一个未知数,且未知数的次数都是1,等号两边都是整式。√√×√××√×思考想一想:⑴使得方程4x=24成立的x的值为多少?当x=6时,方程4x=24成立。(2)使得方程5x+2=12成立的x的值为多少?当x=2时,方程5x+2=12成立。方程的解:使方程中等号左右两边相等的未知数的值叫方程的解。x=1和x=5哪一个是方程1700+150x=2450的解? 实践练习解:当x=1时 方程的左边=1700+150×1
=1700+150=1850方程的左边≠右边,所以x=1不是方程1700+150x=2450的解。当x=5时方程的左边=1700+150×5=2450方程的左边=右边,所以x=5是方程1700+150x=2450的解。1、方程(a+6)x2 +3x-8=7是关于x的一元一次方程,则a= _____。2、列方程:某数χ的相反数比它的 大1,求某数。 -63、一元一次方程2x-3=5的解是( )
A、4 B、5 C、6 D、7A我掌握,我巩固4、x=2是下列哪个方程的解? .
(1) 3x-1=2x+1
(2) 3x+1=2x-1
(3) 3x+2x-2=0
(4) x-2=0
(1)(4) 5、根据下列问题,设未知数,列出方程:(1)、环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?(2)、甲种铅笔每枝0.3元,乙种铅笔每枝0.6元,用9元钱买了两种铅笔共20枝,两种铅笔各买了多少枝?(3)、一个梯形的下底比上底多2㎝,高是5㎝,面积是40㎝2,求上底. 智力闯关,谁是英雄第一关 是一元一次方程,则k=_______第二关: 是一元一次方程,则k=______第三关 : 是一元一次方程,则k=__: 第四关: 是一元一次方程,则k =____21或-1-1-2一种方法——列方程解决实际问题的方法;
三个概念——方程、一元一次方程、方程
的解;我收获,我总结1、通过本节的学习你有什么收获? 2、在这部分学习中,你还有什么困难?感悟 1、在一卷公元前1600年左右遗留下来的古埃及草卷中, 记载着一些数学问题.其中一个翻译过来就是“啊哈,它的全部,它的七分之一, 其和等于19”.你能求出问题中的“它”吗?请你能根据题意列出方程.设 :“它”为x,列出方程: x+ =19挑战时刻百羊问题:
2、我国明代数学家程大为曾提出过这样一个有趣问题。有一个人赶着一群羊在前面走,另一个人牵着一头羊跟在后面。后面的人问赶羊的人说:“你这群羊有一百只吗?”赶羊的人回答:“我如果再得这么一群羊,再得这么一群羊的一半,又再得这群羊的四分之一,把你牵的羊也给我,我恰好有一百只。”请问这群羊有多少头? 解:设这群羊有x只, 可列出方程:
x+x+ + +1=100上有20头、 下有52足,问鸡兔各有多少?自主探索~~~鸡兔同笼 思 维 拓 宽请看一例 2004年夏季奥运会上,我国获得32枚金牌。其中跳水队获得6枚金牌,比射击队获得金牌数的2倍少2枚。射击队获得多少枚金牌?跳水队比射 击队的 2倍 少2
枚
6=2x-2如果设射击队获得的金牌数为x练一练(根据下列问题中的条件列出方程)设这件衣服的原价为x元,
可列出方程 。 练一练(根据下列问题中的条件列出方程)2008年北京奥运会
的足球分赛场---秦
皇岛市奥体中心体
育场,其足球场的
周长为344米,长和
宽之差为36米,这
个足球场的长与宽
分别是多少米?设这个足球场的宽为x米,则长
为(x+36)米,可列出方程
。
