物理人教版(2019)选择性必修第二册1.3带电粒子在匀强磁场中的运动课件(共16张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册1.3带电粒子在匀强磁场中的运动课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-29 16:11:11 | ||
图片预览






文档简介
(共16张PPT)
第一章 安培力与洛伦兹力
第3节 带电粒子在匀强磁场中的运动
在现代科学技术中,常常要研究带电粒子在磁场中的运动。如果沿着与磁场垂直的方向发射一束带电粒子,请猜想这束粒子在匀强磁场中的运动径迹?
情境与思考
F
思考2:洛伦兹力的方向总与速度方向?
思考1:由于是匀强磁场,洛伦兹力大小?
不变
垂直
思考3:洛伦兹力只会改变粒子速度的 ,
不改变速度的 ,故粒子将做
方向
大小
匀速圆周运动
洛伦兹力对电荷做功吗?
不做功
实验:用洛伦兹力演示仪观察运动的电子在磁场中的偏转
励磁线圈
电子枪
加速极电压
②励磁线圈:
①加速电场:
励磁线圈侧视图
改变电子束出射的速度
能在两线圈之间产生平行于两线圈中心连线的匀强磁场
2. 给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由读者指向纸面的磁场。
实验:用洛伦兹力演示仪观察运动的电子在磁场中的偏转
分别预测下列情况下带电粒子的运动径迹:
1. 不加磁场。
3. 保持出射电子的速度不变,改变磁感应强度。
4. 保持磁感应强度不变,改变出射电子的速度大小和方向。
2. 给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由读者指向纸面的磁场。
实验:用洛伦兹力演示仪观察运动的电子在磁场中的偏转
实验后可知下列情况下带电粒子的运动径迹:
1. 不加磁场。
直线
匀速圆周运动
励磁电流增大时B增大,圆周运动的半径减小;
反之半径增大。
加大加速极电压时电子速度增大,圆周运动的半径
增大;反之半径减小。
3. 保持出射电子的速度不变,改变磁感应强度。
4. 保持磁感应强度不变,改变出射电子的速度大小和方向。
B ↑
r ↓
v ↑
r ↑
带电粒子在匀强磁场中的运动
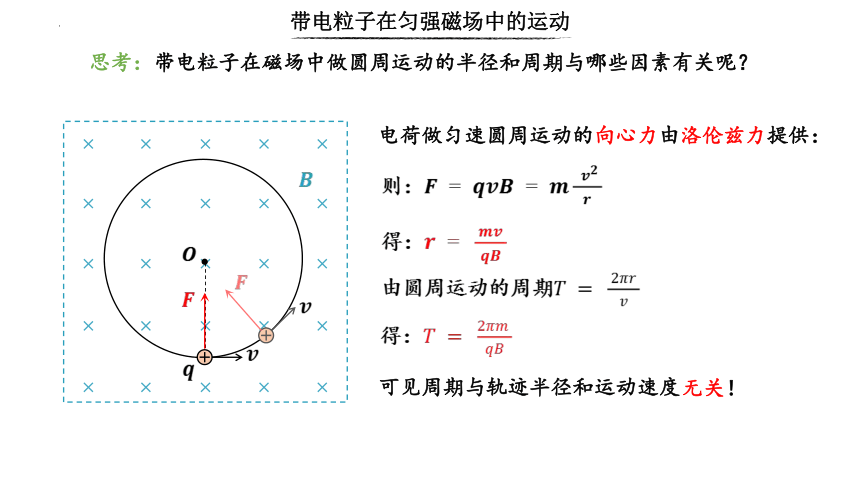
思考:带电粒子在磁场中做圆周运动的半径和周期与哪些因素有关呢?
电荷做匀速圆周运动的向心力由洛伦兹力提供:
则:
得:
由圆周运动的周期
得:
可见周期与轨迹半径和运动速度
无关!
带电粒子在匀强磁场中的运动
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例1. 一个质量为1.67×10-27kg、电荷量为1.6×10-19C的带电粒子,以5×105m/s的初速度沿与磁场垂直的方向射入磁感应强度为0.2T的匀强磁场。求:
(1)粒子所受的重力和洛伦兹力的大小之比;
(2)粒子在磁场中运动的轨道半径;
(3)粒子做匀速圆周运动的周期。
1.03×10-12,洛伦兹力远大于重力
2.61×10-2m
3.28×10-7s
P
Q
v0
v0
B
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间
O
1. 圆心的确定
(1)已知入射方向和出射方向:
作入射速度和出射速度的垂线,
两垂线交点即圆周运动的圆心
作入射速度垂线和弦的中垂线,
交点即圆周运动的圆心
P
Q
v0
B
O
(2)已知入射方向和出射点的位置:
2. 半径的确定
方法一:已知物理量(q、m、B、v),利用公式求半径
方法二:已知其他几何量利用数学图形知识求半径,一般利用几何知识,常用
解三角形的方法
3. 运动时间的确定
利用圆心角与弦切角的关系,或者四边形内角和等计算出圆心角的大小,
由公式可求出运动时间:
(θ单位为度)
(θ单位为弧度)
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间
圆心角(α)等于偏向角(φ) ,并等于AB弦与切线的夹角(弦切角θ)的2倍:
α = φ = 2θ
带电粒子在匀强磁场中的运动
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例1. 正方形容器处于匀强磁场中,一群速率不同的α粒子沿a→d方向垂直射入匀强磁场中,有的从b孔射出,有的从c孔射出,则从b、c射出的α粒子在磁场中的:
(1)速度之比vb∶vc =
1∶2
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
(2)加速度之比ab∶ac =
(3)运动时间之比tb∶tc =
1∶2
2∶1
×
×
×
×
×
×
×
×
×
a
d
c
b
带电粒子在匀强磁场中的运动
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例2. 如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B,宽度为d的匀强磁场中,穿过磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是________,穿过磁场的时间是________。
2dBe/v
πd/3v
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
磁场边界为直线的问题
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例3. 如图,一足够长的矩形区域abcd内存在磁感应强度为B、方向垂直纸面向里的匀强磁场。现从矩形区域的ab边的中点O处,垂直磁场射入一速度方向跟ab边夹角为30 °的带正电的粒子。已知粒子质量为m,电量为q,ad边长为L,重力影响不计。试求:
(1)粒子能从ab边射出磁场的v0的大小范围;
(2)粒子在磁场中运动的最长时间是多少?
(1)< r ≤ L
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
R1
30°
R2
O1
O2
< v0 ≤
(2) r ≤ R1时,圆心角为(2π-2θ),tM=
磁场边界为圆周的问题
例4. 如图所示,半径r=0.6m的圆形虚线区域内,存在一磁感应强度为B=0.5T的垂直于纸面向外的匀强磁场,有一带电量为q=2×10-10C、质量为m=2×10-15kg的不计重力的粒子进入磁场,问:
(1)若粒子从a点以v0= ×104m/s的速度沿aO方向射入磁场,则它在场中运动的时间和通过的路程各为多大?
(2)若从b点以速度v0=3×104m/s沿与aO平行的bc(c为Od的中点)方向射入,则情况又如何?
①找圆心
②定半径
③确定运动时间:
或
圆心角(α)等于偏向角(φ) ,并等于AB弦与切线的夹角(弦切角θ)的2倍:
α = φ = 2θ
θ1=120°
t1=×10-5 s
s1= m
θ2=60°
t2=×10-5 s
s2= m
“磁聚焦”问题
当带电粒子在磁场中的轨迹半径与磁场区域的半径相等时:
一束速度相等、平行的粒子垂直射入圆形区域的磁场,它们将交于磁场边界上一点。
从圆形区域磁场的边界上一点垂直磁场发散射出的、速率相等的粒子,将从磁场平行射出。
磁场范围确定的问题
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例5. 一匀强磁场,磁场方向垂直于xOy平面,在xOy平面上,磁场分布在一个圆形区域内。一个质量为m、电荷量为q的带电粒子,有原点O以大小为v、方向沿x正方向的初速度开始射入磁场。后来粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示。不计重力的影响。求:
(1)磁场的磁感应强度B的大小;
(2)xOy平面上磁场区域的最小面积S。
B =
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
S =
y
x
P
L
30°
)
v
O
r
r
A
同学们,下课!
第一章 安培力与洛伦兹力
第3节 带电粒子在匀强磁场中的运动
在现代科学技术中,常常要研究带电粒子在磁场中的运动。如果沿着与磁场垂直的方向发射一束带电粒子,请猜想这束粒子在匀强磁场中的运动径迹?
情境与思考
F
思考2:洛伦兹力的方向总与速度方向?
思考1:由于是匀强磁场,洛伦兹力大小?
不变
垂直
思考3:洛伦兹力只会改变粒子速度的 ,
不改变速度的 ,故粒子将做
方向
大小
匀速圆周运动
洛伦兹力对电荷做功吗?
不做功
实验:用洛伦兹力演示仪观察运动的电子在磁场中的偏转
励磁线圈
电子枪
加速极电压
②励磁线圈:
①加速电场:
励磁线圈侧视图
改变电子束出射的速度
能在两线圈之间产生平行于两线圈中心连线的匀强磁场
2. 给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由读者指向纸面的磁场。
实验:用洛伦兹力演示仪观察运动的电子在磁场中的偏转
分别预测下列情况下带电粒子的运动径迹:
1. 不加磁场。
3. 保持出射电子的速度不变,改变磁感应强度。
4. 保持磁感应强度不变,改变出射电子的速度大小和方向。
2. 给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由读者指向纸面的磁场。
实验:用洛伦兹力演示仪观察运动的电子在磁场中的偏转
实验后可知下列情况下带电粒子的运动径迹:
1. 不加磁场。
直线
匀速圆周运动
励磁电流增大时B增大,圆周运动的半径减小;
反之半径增大。
加大加速极电压时电子速度增大,圆周运动的半径
增大;反之半径减小。
3. 保持出射电子的速度不变,改变磁感应强度。
4. 保持磁感应强度不变,改变出射电子的速度大小和方向。
B ↑
r ↓
v ↑
r ↑
带电粒子在匀强磁场中的运动
思考:带电粒子在磁场中做圆周运动的半径和周期与哪些因素有关呢?
电荷做匀速圆周运动的向心力由洛伦兹力提供:
则:
得:
由圆周运动的周期
得:
可见周期与轨迹半径和运动速度
无关!
带电粒子在匀强磁场中的运动
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例1. 一个质量为1.67×10-27kg、电荷量为1.6×10-19C的带电粒子,以5×105m/s的初速度沿与磁场垂直的方向射入磁感应强度为0.2T的匀强磁场。求:
(1)粒子所受的重力和洛伦兹力的大小之比;
(2)粒子在磁场中运动的轨道半径;
(3)粒子做匀速圆周运动的周期。
1.03×10-12,洛伦兹力远大于重力
2.61×10-2m
3.28×10-7s
P
Q
v0
v0
B
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间
O
1. 圆心的确定
(1)已知入射方向和出射方向:
作入射速度和出射速度的垂线,
两垂线交点即圆周运动的圆心
作入射速度垂线和弦的中垂线,
交点即圆周运动的圆心
P
Q
v0
B
O
(2)已知入射方向和出射点的位置:
2. 半径的确定
方法一:已知物理量(q、m、B、v),利用公式求半径
方法二:已知其他几何量利用数学图形知识求半径,一般利用几何知识,常用
解三角形的方法
3. 运动时间的确定
利用圆心角与弦切角的关系,或者四边形内角和等计算出圆心角的大小,
由公式可求出运动时间:
(θ单位为度)
(θ单位为弧度)
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间
圆心角(α)等于偏向角(φ) ,并等于AB弦与切线的夹角(弦切角θ)的2倍:
α = φ = 2θ
带电粒子在匀强磁场中的运动
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例1. 正方形容器处于匀强磁场中,一群速率不同的α粒子沿a→d方向垂直射入匀强磁场中,有的从b孔射出,有的从c孔射出,则从b、c射出的α粒子在磁场中的:
(1)速度之比vb∶vc =
1∶2
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
(2)加速度之比ab∶ac =
(3)运动时间之比tb∶tc =
1∶2
2∶1
×
×
×
×
×
×
×
×
×
a
d
c
b
带电粒子在匀强磁场中的运动
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例2. 如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B,宽度为d的匀强磁场中,穿过磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是________,穿过磁场的时间是________。
2dBe/v
πd/3v
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
磁场边界为直线的问题
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例3. 如图,一足够长的矩形区域abcd内存在磁感应强度为B、方向垂直纸面向里的匀强磁场。现从矩形区域的ab边的中点O处,垂直磁场射入一速度方向跟ab边夹角为30 °的带正电的粒子。已知粒子质量为m,电量为q,ad边长为L,重力影响不计。试求:
(1)粒子能从ab边射出磁场的v0的大小范围;
(2)粒子在磁场中运动的最长时间是多少?
(1)< r ≤ L
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
R1
30°
R2
O1
O2
< v0 ≤
(2) r ≤ R1时,圆心角为(2π-2θ),tM=
磁场边界为圆周的问题
例4. 如图所示,半径r=0.6m的圆形虚线区域内,存在一磁感应强度为B=0.5T的垂直于纸面向外的匀强磁场,有一带电量为q=2×10-10C、质量为m=2×10-15kg的不计重力的粒子进入磁场,问:
(1)若粒子从a点以v0= ×104m/s的速度沿aO方向射入磁场,则它在场中运动的时间和通过的路程各为多大?
(2)若从b点以速度v0=3×104m/s沿与aO平行的bc(c为Od的中点)方向射入,则情况又如何?
①找圆心
②定半径
③确定运动时间:
或
圆心角(α)等于偏向角(φ) ,并等于AB弦与切线的夹角(弦切角θ)的2倍:
α = φ = 2θ
θ1=120°
t1=×10-5 s
s1= m
θ2=60°
t2=×10-5 s
s2= m
“磁聚焦”问题
当带电粒子在磁场中的轨迹半径与磁场区域的半径相等时:
一束速度相等、平行的粒子垂直射入圆形区域的磁场,它们将交于磁场边界上一点。
从圆形区域磁场的边界上一点垂直磁场发散射出的、速率相等的粒子,将从磁场平行射出。
磁场范围确定的问题
1. 电荷做匀速圆周运动的向心力由洛伦兹力提供:
得:
2. 由圆周运动的周期
得:
例5. 一匀强磁场,磁场方向垂直于xOy平面,在xOy平面上,磁场分布在一个圆形区域内。一个质量为m、电荷量为q的带电粒子,有原点O以大小为v、方向沿x正方向的初速度开始射入磁场。后来粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示。不计重力的影响。求:
(1)磁场的磁感应强度B的大小;
(2)xOy平面上磁场区域的最小面积S。
B =
3. 带电粒子在磁场中运动情况的研究方法
①找圆心
②定半径
③确定运动时间:
或
S =
y
x
P
L
30°
)
v
O
r
r
A
同学们,下课!
