13.3.2 等边三角形一课一练(含解析)
文档属性
| 名称 | 13.3.2 等边三角形一课一练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 11:04:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.3.2 等边三角形一课一练
一、填空题
1.如上图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD=
二、单选题
2.如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是( )
A.BP是∠ABC的平分线 B.AD=BD
C. D.CD=BD
3.如图,在中,,则的面积为( )
A.4 B.6 C.8 D.16
4.若等边△ABC的边长为2,那么△ABC的面积为( )
A. B.2 C.3 D.4
5.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,则AC长为( )
A.4 B.2 C.1 D.
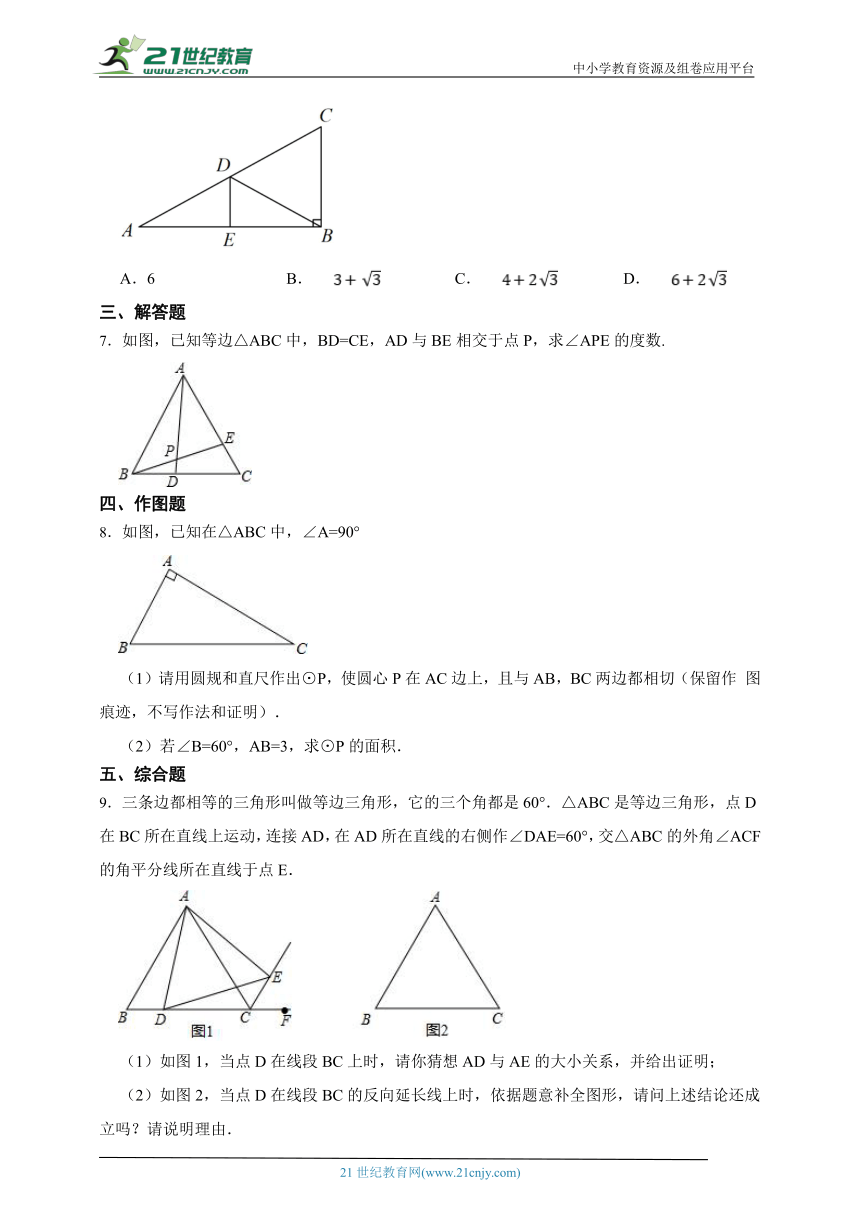
6.如图,在中,,,,点D是边AC的中点,点E是边AB的中点,则的周长是( )
A.6 B. C. D.
三、解答题
7.如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,求∠APE的度数.
四、作图题
8.如图,已知在△ABC中,∠A=90°
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作 图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
五、综合题
9.三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.
六、实践探究题
10.根据要求回答问题:
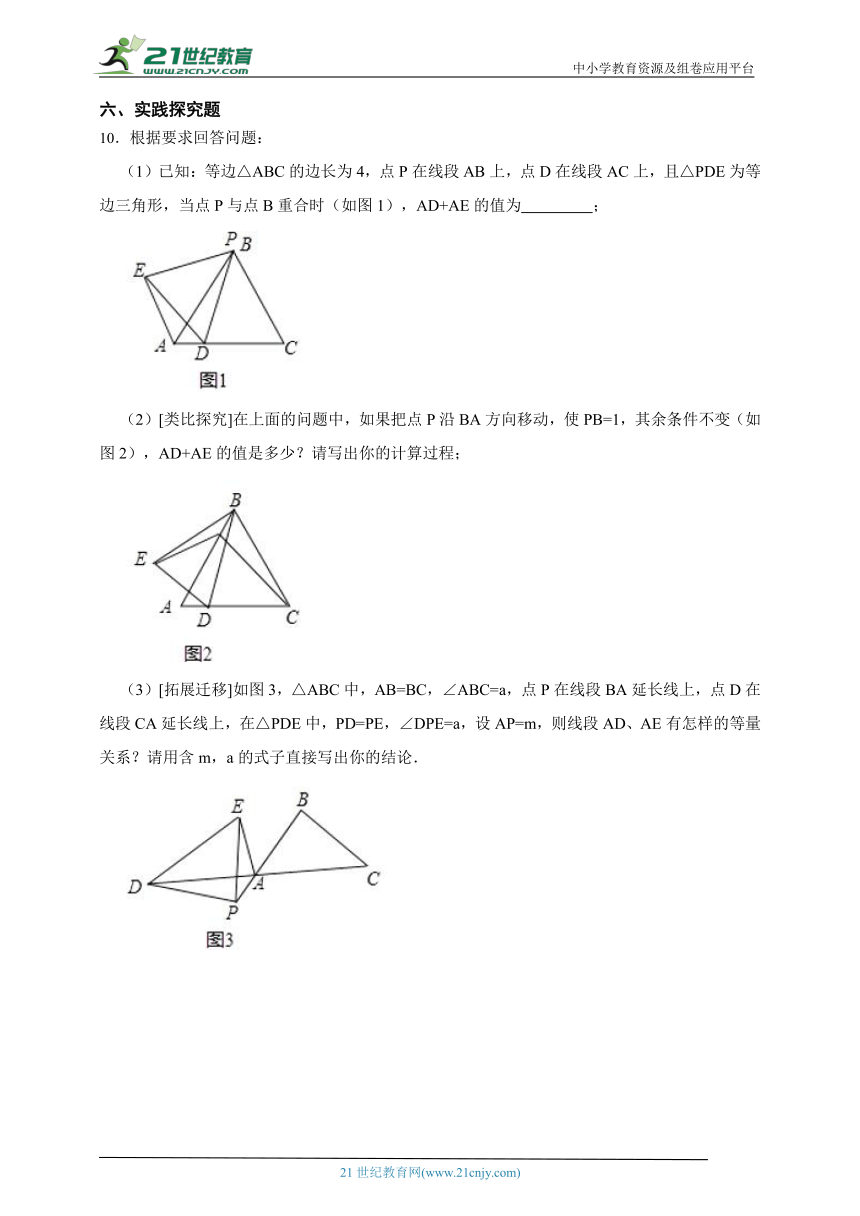
(1)已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为 ;
(2)[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程;
(3)[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论.
答案解析部分
1.【答案】3
【解析】【解答】如图,过点P作PE⊥OA于E,
∵∠AOB=30°,OP平分∠AOB,
∴∠AOP=∠BOP=15°.
∵PC∥OB,
∴∠BOP=∠OPC=15°,
∴∠PCE=∠AOP+∠OPC=15°+15°=30°,
又∵PC=6,
∴PE=PC=3,
∵∠AOP=∠BOP,PD⊥OB于D,PE⊥OA于E,
∴PD=PE=3,
故答案为3.
【分析】过点P作PE⊥OA于E,先求出∠PCE=∠AOP+∠OPC=15°+15°=30°,再利用含30°角的直角三角形的性质可得PE=PC=3,再根据PD=PE即可得到答案。
2.【答案】C
【解析】【解答】解:根据作图可得BD平分∠ABC,故A正确;
∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∴∠ABD=30°=∠A,
∴AD=BD,故B正确;
∵∠CBD=∠ABC=30°,
∴BD=2CD,故D;
∴AD=2CD,
∴S△ABD=2S△CBD,故C错误.
故答案为:C.
【分析】根据作图即可判断A,根据角平分线的性质即可判断B,根据含30度角的直角三角形的性质,即可判断CD,
3.【答案】A
【解析】【解答】解:如图,
过点C作CD⊥AB交BA的延长线于D,
∵∠B=∠ACB=15°,AB=AC=4,
∴∠CAD=∠B+∠ACB=15°+15°=30°,
∴CD=AC=×4=2,
∴△ABC的面积=AB CD=×4×2=4,
故答案为:A.
【分析】过点C作CD⊥AB交BA的延长线于D,先求出∠CAD=∠B+∠ACB=15°+15°=30°,再利用含30°角的直角三角形的性质求出CD的长,最后利用三角形的面积公式可得答案。
4.【答案】A
【解析】【解答】解:过点A作AD⊥BC,交BC于点D,如图,
因为是等边三角形,
所以可知BD=CD= BC=1,
在Rt△ABD中,由勾股定理可知AD= ,
所以 ,
故选:A.
【分析】利用等边三角形的三线合一,作出一边上的高,再利用勾股定理求出高的长度,即可计算出三角形的面积.
5.【答案】C
【解析】【解答】解:∵在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,
∴AC= AB=1.
故选C.
【分析】根据直角三角形30°角所对的直角边等于斜边的一半得出AC= AB=1.
6.【答案】B
【解析】【解答】在Rt△ABC中,∠A=30°,BC=2,
∴AC=2BC=4,
则,
即.
∵点D,E是AC,AB的中点,
∴AD=2,,DE是△ABC的中位线,
∴,,
∴DE⊥AB,
∴DE是AB的垂直平分线,
∴BD=AD=2,
∴△BDE的周长=.
故答案为:B.
【分析】根据含30°角的直角三角形的性质可得AC=2BC=4,利用勾股定理求出AB的长,再结合DE是AB的垂直平分线,可得BD=AD=2,最后利用三角形的周长公式计算即可。
7.【答案】解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中, ,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE.
∵∠APE=∠ABP+∠BAP,
∴∠APE=∠ABP+∠CBE=∠ABC=60°.
【解析】【分析】根据等边三角形的性质可得AB=BC,∠ABC=∠C=60°,根据“SAS”可得△ABD≌△BCE,可得∠BAD=∠CBE.根据三角形外角的性质可得∠APE=∠ABP+∠BAP=∠ABP+∠CBE=∠ABC,从而求出结论.
8.【答案】(1)解:如图所示,则⊙P为所求作的圆.
(2)解:∵∠B=60°,BP平分∠ABC,
∴∠ABP=30°, ∴AP= ,∴S⊙P=3π
【解析】【分析】(1)根据角平分线上的点到角两边的距离相等,作出∠ABC的角平分线,交AC于点P,以点P为圆心,PA的长为半径,画圆,该圆就是所求的圆;
(2)根据角平分线的定义得出∠ABP=30°,根据含30 直角三角形的边之间的关系得出AP 的长,再根据圆的面积计算方法即可算出答案。
9.【答案】(1)结论:AD=AE.
理由:如图,在AB上取一点M,使BM=BD,连接MD.
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠2+∠ADE=∠1+∠B
∴∠1=∠2.
又∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中,
,
∴△AMD≌△DCE(ASA).
∴AD=DE.
(2)正确.
证明:延长BA到M,使AM=CD,
与(1)相同,可证△BDM是等边三角形,
∵∠CDE=∠ADB+∠ADE=∠ADB+60°,
∠MAD=∠B+∠ADB=∠ADB+60°,
∴∠CDE=∠MAD,
同理可证,△AMD≌△DCE,
∴AD=DE.
【解析】【分析】(1)在AB上取一点M,使BM=BD,连接MD.则△BDM是等边三角形,则易证AM=DC,根据ASA即可证得△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得;(2)延长BA到M,使AM=CD,与(1)相同,可证△BDM是等边三角形,然后证明△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得.
10.【答案】(1)4
(2)解:AD+AE=3
理由:如图2中,作PK∥BC交AC于K.连接AE.
易证△PAK是等边三角形,
由上面题目可知.AE+AD=AK=3
(3)解:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.
易证∠APK=∠DPE=α,
∵PD=PE,PK=PA,
∴∠DPK=∠EPA,
∴△PDK≌△PEA,
∴DK=AE,
∴AD﹣AE=AK=2AJ=2 m sin .
∴AD﹣AE=2m sin
【解析】【解答】(1)解:如图1中,
∵△PDE.△PAC都是等边三角形,
∴PE=PD,PA=PC,∠EPD=∠APC=60°,
∴∠EPA=∠DPC,
∴△EPA≌△DPC,
∴AE=CD,
∴AD+AE=AD+DC=AC=4.
【分析】(1)只要证明△EPA≌△DPC,即可推出AE=CD,可得AD+AE=AD+DC=AC=4;(2)[类比探究]:如图2中,作PK∥BC交AC于K.连接AE.利用(1)中的结论即可解决问题;(3)[拓展迁移]:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.由△PDK≌△PEA,推出DK=AE,推出AD﹣AE=AK=2AJ=2 m sin 即可解决问题;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
13.3.2 等边三角形一课一练
一、填空题
1.如上图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD=
二、单选题
2.如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是( )
A.BP是∠ABC的平分线 B.AD=BD
C. D.CD=BD
3.如图,在中,,则的面积为( )
A.4 B.6 C.8 D.16
4.若等边△ABC的边长为2,那么△ABC的面积为( )
A. B.2 C.3 D.4
5.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,则AC长为( )
A.4 B.2 C.1 D.
6.如图,在中,,,,点D是边AC的中点,点E是边AB的中点,则的周长是( )
A.6 B. C. D.
三、解答题
7.如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,求∠APE的度数.
四、作图题
8.如图,已知在△ABC中,∠A=90°
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作 图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
五、综合题
9.三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.
六、实践探究题
10.根据要求回答问题:
(1)已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为 ;
(2)[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程;
(3)[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论.
答案解析部分
1.【答案】3
【解析】【解答】如图,过点P作PE⊥OA于E,
∵∠AOB=30°,OP平分∠AOB,
∴∠AOP=∠BOP=15°.
∵PC∥OB,
∴∠BOP=∠OPC=15°,
∴∠PCE=∠AOP+∠OPC=15°+15°=30°,
又∵PC=6,
∴PE=PC=3,
∵∠AOP=∠BOP,PD⊥OB于D,PE⊥OA于E,
∴PD=PE=3,
故答案为3.
【分析】过点P作PE⊥OA于E,先求出∠PCE=∠AOP+∠OPC=15°+15°=30°,再利用含30°角的直角三角形的性质可得PE=PC=3,再根据PD=PE即可得到答案。
2.【答案】C
【解析】【解答】解:根据作图可得BD平分∠ABC,故A正确;
∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∴∠ABD=30°=∠A,
∴AD=BD,故B正确;
∵∠CBD=∠ABC=30°,
∴BD=2CD,故D;
∴AD=2CD,
∴S△ABD=2S△CBD,故C错误.
故答案为:C.
【分析】根据作图即可判断A,根据角平分线的性质即可判断B,根据含30度角的直角三角形的性质,即可判断CD,
3.【答案】A
【解析】【解答】解:如图,
过点C作CD⊥AB交BA的延长线于D,
∵∠B=∠ACB=15°,AB=AC=4,
∴∠CAD=∠B+∠ACB=15°+15°=30°,
∴CD=AC=×4=2,
∴△ABC的面积=AB CD=×4×2=4,
故答案为:A.
【分析】过点C作CD⊥AB交BA的延长线于D,先求出∠CAD=∠B+∠ACB=15°+15°=30°,再利用含30°角的直角三角形的性质求出CD的长,最后利用三角形的面积公式可得答案。
4.【答案】A
【解析】【解答】解:过点A作AD⊥BC,交BC于点D,如图,
因为是等边三角形,
所以可知BD=CD= BC=1,
在Rt△ABD中,由勾股定理可知AD= ,
所以 ,
故选:A.
【分析】利用等边三角形的三线合一,作出一边上的高,再利用勾股定理求出高的长度,即可计算出三角形的面积.
5.【答案】C
【解析】【解答】解:∵在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,
∴AC= AB=1.
故选C.
【分析】根据直角三角形30°角所对的直角边等于斜边的一半得出AC= AB=1.
6.【答案】B
【解析】【解答】在Rt△ABC中,∠A=30°,BC=2,
∴AC=2BC=4,
则,
即.
∵点D,E是AC,AB的中点,
∴AD=2,,DE是△ABC的中位线,
∴,,
∴DE⊥AB,
∴DE是AB的垂直平分线,
∴BD=AD=2,
∴△BDE的周长=.
故答案为:B.
【分析】根据含30°角的直角三角形的性质可得AC=2BC=4,利用勾股定理求出AB的长,再结合DE是AB的垂直平分线,可得BD=AD=2,最后利用三角形的周长公式计算即可。
7.【答案】解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中, ,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE.
∵∠APE=∠ABP+∠BAP,
∴∠APE=∠ABP+∠CBE=∠ABC=60°.
【解析】【分析】根据等边三角形的性质可得AB=BC,∠ABC=∠C=60°,根据“SAS”可得△ABD≌△BCE,可得∠BAD=∠CBE.根据三角形外角的性质可得∠APE=∠ABP+∠BAP=∠ABP+∠CBE=∠ABC,从而求出结论.
8.【答案】(1)解:如图所示,则⊙P为所求作的圆.
(2)解:∵∠B=60°,BP平分∠ABC,
∴∠ABP=30°, ∴AP= ,∴S⊙P=3π
【解析】【分析】(1)根据角平分线上的点到角两边的距离相等,作出∠ABC的角平分线,交AC于点P,以点P为圆心,PA的长为半径,画圆,该圆就是所求的圆;
(2)根据角平分线的定义得出∠ABP=30°,根据含30 直角三角形的边之间的关系得出AP 的长,再根据圆的面积计算方法即可算出答案。
9.【答案】(1)结论:AD=AE.
理由:如图,在AB上取一点M,使BM=BD,连接MD.
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠2+∠ADE=∠1+∠B
∴∠1=∠2.
又∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中,
,
∴△AMD≌△DCE(ASA).
∴AD=DE.
(2)正确.
证明:延长BA到M,使AM=CD,
与(1)相同,可证△BDM是等边三角形,
∵∠CDE=∠ADB+∠ADE=∠ADB+60°,
∠MAD=∠B+∠ADB=∠ADB+60°,
∴∠CDE=∠MAD,
同理可证,△AMD≌△DCE,
∴AD=DE.
【解析】【分析】(1)在AB上取一点M,使BM=BD,连接MD.则△BDM是等边三角形,则易证AM=DC,根据ASA即可证得△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得;(2)延长BA到M,使AM=CD,与(1)相同,可证△BDM是等边三角形,然后证明△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得.
10.【答案】(1)4
(2)解:AD+AE=3
理由:如图2中,作PK∥BC交AC于K.连接AE.
易证△PAK是等边三角形,
由上面题目可知.AE+AD=AK=3
(3)解:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.
易证∠APK=∠DPE=α,
∵PD=PE,PK=PA,
∴∠DPK=∠EPA,
∴△PDK≌△PEA,
∴DK=AE,
∴AD﹣AE=AK=2AJ=2 m sin .
∴AD﹣AE=2m sin
【解析】【解答】(1)解:如图1中,
∵△PDE.△PAC都是等边三角形,
∴PE=PD,PA=PC,∠EPD=∠APC=60°,
∴∠EPA=∠DPC,
∴△EPA≌△DPC,
∴AE=CD,
∴AD+AE=AD+DC=AC=4.
【分析】(1)只要证明△EPA≌△DPC,即可推出AE=CD,可得AD+AE=AD+DC=AC=4;(2)[类比探究]:如图2中,作PK∥BC交AC于K.连接AE.利用(1)中的结论即可解决问题;(3)[拓展迁移]:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.由△PDK≌△PEA,推出DK=AE,推出AD﹣AE=AK=2AJ=2 m sin 即可解决问题;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
