13.4 课题学习 最短路径问题一课一练(含解析)
文档属性
| 名称 | 13.4 课题学习 最短路径问题一课一练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 787.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 11:05:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
13.4课题学习 最短路径问题一课一练
一、单选题
1.如图,中,,垂直平分,点P为直线上一动点,则的最小值为( )
A.3 B.5 C.6 D.7
2.数学课上,老师提出如下问题:
如图1,点P、Q是直线l同侧的两点,请你在直线l上确定一个点R.使 的周长最小.小明的作法如下,如图2:
( 1 )作点Q关于直线l的对称点 ;
( 2 )连接 ,交直线l于点R;
( 3 )连接RQ、PQ.
那么点R就是使 的周长最小的点.
老师说,小明的做法正确.接着.老师问同学们,小明这种作法应用了哪些我们学过的定理呢?有四位同学分别说了一个定理,下面的A,B,C,D四个答案分别代表了四个同学所说的定理,其中小明没有应用到的定理是( )
A.如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线
B.等腰三角形底边上的高也是顶角的角平分线
C.线段垂直平分线上的点到线段两个端点的距离相等
D.两点之间,线段最短
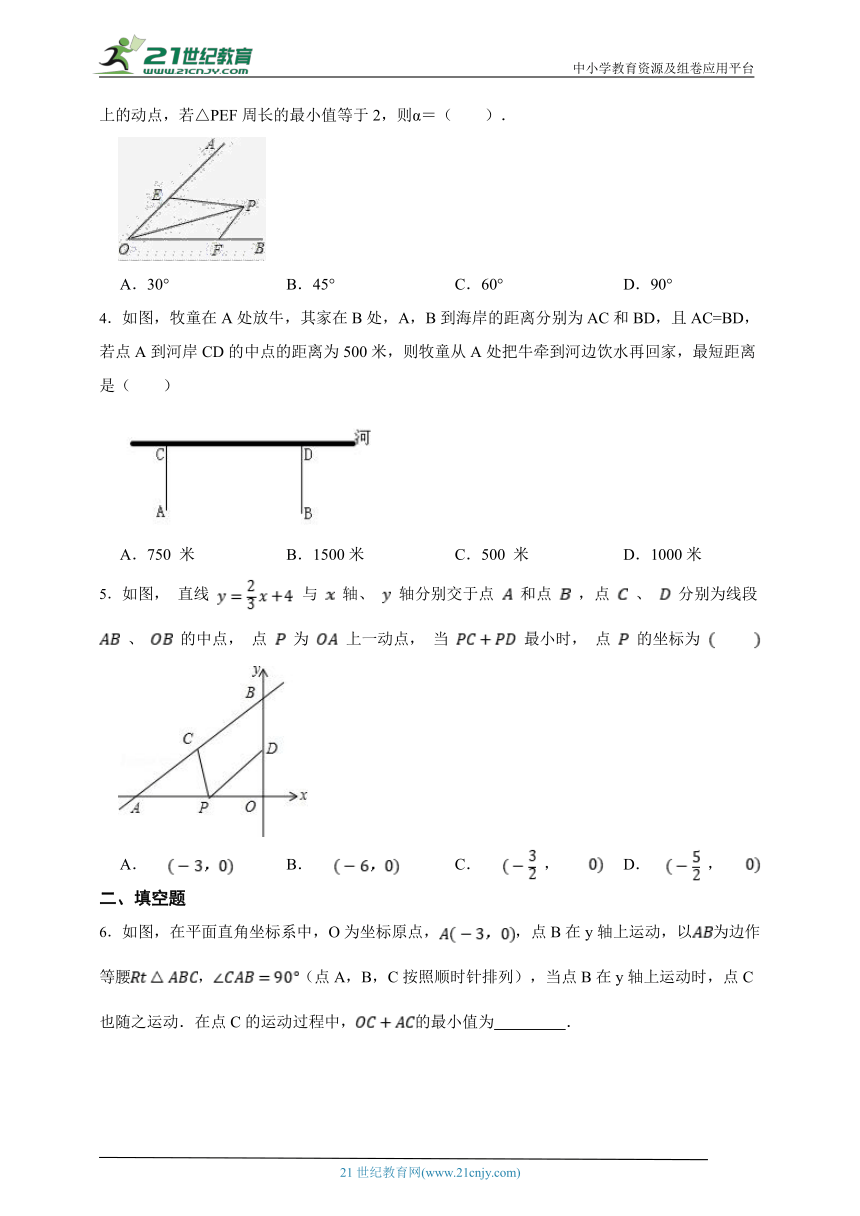
3.已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( ).
A.30° B.45° C.60° D.90°
4.如图,牧童在A处放牛,其家在B处,A,B到海岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )
A.750 米 B.1500米 C.500 米 D.1000米
5.如图, 直线 与 轴、 轴分别交于点 和点 ,点 、 分别为线段 、 的中点, 点 为 上一动点, 当 最小时, 点 的坐标为
A. B. C. , D. ,
二、填空题
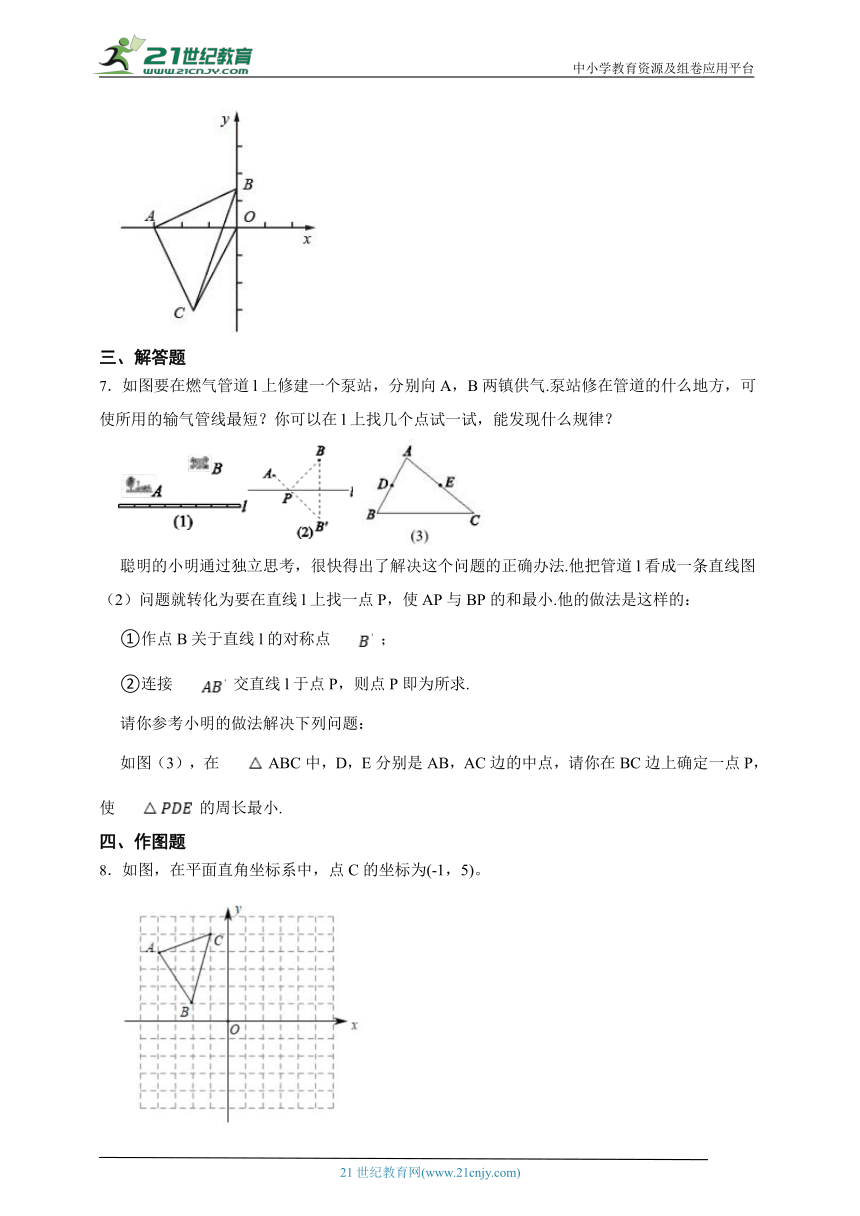
6.如图,在平面直角坐标系中,O为坐标原点,,点B在y轴上运动,以为边作等腰,(点A,B,C按照顺时针排列),当点B在y轴上运动时,点C也随之运动.在点C的运动过程中,的最小值为 .
三、解答题
7.如图要在燃气管道l上修建一个泵站,分别向A,B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律?
聪明的小明通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线图(2)问题就转化为要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点 ;
②连接 交直线l于点P,则点P即为所求.
请你参考小明的做法解决下列问题:
如图(3),在 ABC中,D,E分别是AB,AC边的中点,请你在BC边上确定一点P,使 的周长最小.
四、作图题
8.如图,在平面直角坐标系中,点C的坐标为(-1,5)。
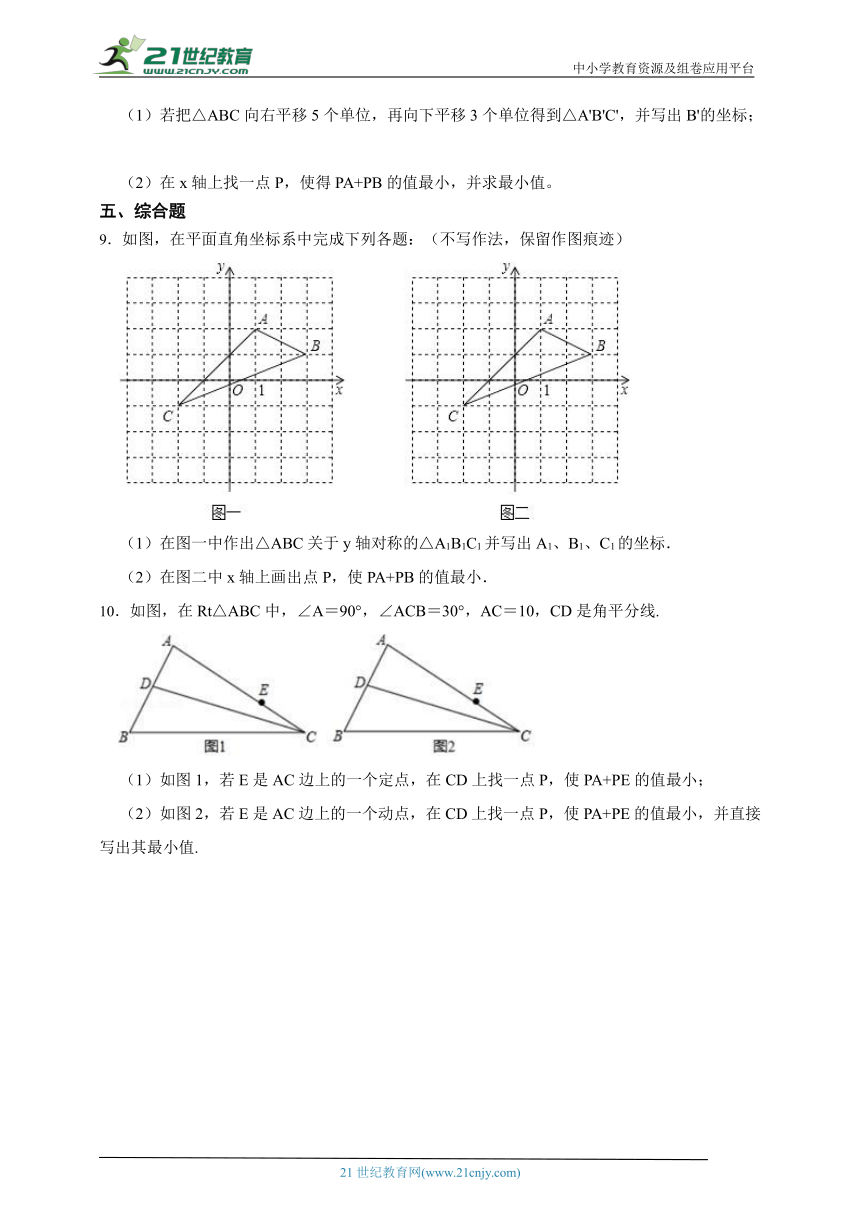
(1)若把△ABC向右平移5个单位,再向下平移3个单位得到△A'B'C',并写出B'的坐标;
(2)在x轴上找一点P,使得PA+PB的值最小,并求最小值。
五、综合题
9.如图,在平面直角坐标系中完成下列各题:(不写作法,保留作图痕迹)
(1)在图一中作出△ABC关于y轴对称的△A1B1C1并写出A1、B1、C1的坐标.
(2)在图二中x轴上画出点P,使PA+PB的值最小.
10.如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.
答案解析部分
1.【答案】B
【解析】【解答】解:∵垂直平分,
∴关于对称,
设交于D,
∴当P和D重合时,的值最小,最小值等于的长,
的最小值是5.
故答案为:B.
【分析】设交于D,当P和D重合时,的值最小,最小值等于的长,再求解即可。
2.【答案】B
【解析】【解答】解:作点Q关于直线l的对称点 ,可得直线l是 的垂直平分线,用到定理为:如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线,故A不符合题意;
由 ,用到的定理为:线段垂直平分线上的点到线段两个端点的距离相等,故C不符合题意;
从而得出QR+PR= +PR
根据两点之间线段最短,可得 的长即为QR+PR的最小值,故D不符合题意;
没有用到B选项定理,故B符合题意.
故答案为:B.
【分析】根据轴对称的性质可得直线l是 的垂直平分线,从而判断A选项;然后得出 ,从而判断C选项;最后根据两点之间线段最短可得 的长即为QR+PR的最小值,从而判断D选项,即可得出结论.
3.【答案】A
【解析】解答:如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=OP=2,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,
∴OC=OD=CD=2,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故选A.
分析:设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=2可求出α的度数.
4.【答案】D
【解析】【解答】解:作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.
由题意:AC=BD,所以A′C=BD,
所以CM=DM,M为CD的中点,
易得△A′CM≌△BDM,
∴A′M=BM
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=2A′M=1000米.
故最短距离是1000米.
故答案为:D.
【分析】根据轴对称的性质和“两点之间线段最短”,连接A′B,得到最短距离为A′B,再根据全等三角形的性质和A到河岸CD的中点的距离为500米,即可求出A'B的值.
5.【答案】C
【解析】【解答】解:(方法一)如图所示
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y= x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= x+4中y=0,则 x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段A
B、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(-3,2),D′(0,-2),
∴有 ,解得: ,
∴直线CD′的解析式为y= ,
令y= 中y=0,则0= 解得:x= ,
∴点P的坐标为 .
故答案为:C.
(方法二)如图所示
连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y= 中x=0,则y=4,
∴点B的坐标为(0,4);
令y= 中y=0,则 =0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为( ).
故答案为:C.
【分析】(方法一)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
(方法二)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,根据三角形中位线定理即可得出点P为线段CD′的中点,由此即可得出点P的坐标.
6.【答案】
【解析】【解答】如图,过点A作直线l⊥x轴,过C,B作CD⊥l于点D,BE⊥l于点E,
∵∠DCA+∠CAD=90°,∠EAB+∠CAD=180°-90°=90°,
∴∠DCA=∠EAB,
又∵∠CDA=∠AEB=90°,AB=AC,
∴ CDA≌ AEB(AAS),
∴BE=AD,
∵,
∴AD=BE=OA=3,
作点A关于CD的对称点A′,连接
,则点
在直线l上,
,
,
∴,
∵在 COA′中,
∴当O,C,A′三点共线时,
有最小值=OA′,此时,OA′=
,
∴最小值=
.
故答案是:
.
【分析】过点A作直线l⊥x轴,过C,B作CD⊥l于点D,BE⊥l于点E,再利用“AAS”证明 CDA≌ AEB可得BE=AD,再作点A关于CD的对称点A′,连接
,则点
在直线l上,
,
,当O,C,A′三点共线时,
有最小值=OA′,此时,OA′=
,即可得到答案。
7.【答案】解:如图所示:
的周长
为 的中位线
,DE为定值
要使 的周长最小
则 的和最小
根据小明的做法,
过点D作关于BC的对称点F,连接EF与线段BC交于P点,
则此时 的和最小,此时 的周长最小.
【解析】【分析】由于DE为定值,只需 的和最小,根据材料提供的方法作图即可,过点D作关于BC的对称点F,连接EF与线段BC交于P点.
8.【答案】(1)解:△A'B'C'如图所示,点B'的坐标为(3,-2);
(2)解:作点A关于x轴的对称点A1,
∴A1的坐标为(-4,-4),
连接BA1,交x轴于点P,则PA+PB=PA1+PB=BA1,点P即为所求.
此时PA+PB的值最小,
最小值=.
【解析】【分析】(1)分别作出A、B、C的对应点A'、B'、C',顺次连接各顶点即可;
(2)作点A关于x轴的对称点A1,连接BA1,交x轴于点P,根据两点之间线段最短,点P即为所求. 把线段BA1放到两直角边分别为5和2个单位长度的直角三角形中,作为斜边,因此BA1即为 PA+PB 的最小值,长度为.
9.【答案】(1)解:如图一所示;
,
由图可知,A1(﹣1,2),B1(﹣3,1),C1(2,﹣1)
(2)解:如图二所示.
【解析】【分析】(1)画出各点关于y轴的对称点,再顺次连接并写出各点坐标即可;(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则点P即为所求点.
10.【答案】(1)解:如图,
过D作DF⊥BC于F,过F作EF⊥AC交CD于P,
则此时,PA+PE的值最小;
点P即为所求
(2)解:如图,过D作DF⊥BC于F,过F作EF⊥AC交CD于P,
则此时,PA+PE的值最小;
PA+PE的最小值=EF,
∵CD是角平分线,∠BAC=90°,
∴DA=DF,
即点A与点F关于CD对称,
∴CF=AC=10,
∵∠ACB=30°,
∴EF= CF=5.
【解析】【分析】(1) 过D作DF⊥BC于F,过F作EF⊥AC交CD于P, 由轴对称的性质可知: 此时PA+PE的值最小,即点P为所求 ;
(2)过D作DF⊥BC于F,过F作EF⊥AC交CD于P,由(1)知此时PA+PE的值最小,由角平分线的性质可得DA=DF,由轴对称的性质可得 CF=AC,再根据直角三角形中30度角所对的直角边等于斜边的一半可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
13.4课题学习 最短路径问题一课一练
一、单选题
1.如图,中,,垂直平分,点P为直线上一动点,则的最小值为( )
A.3 B.5 C.6 D.7
2.数学课上,老师提出如下问题:
如图1,点P、Q是直线l同侧的两点,请你在直线l上确定一个点R.使 的周长最小.小明的作法如下,如图2:
( 1 )作点Q关于直线l的对称点 ;
( 2 )连接 ,交直线l于点R;
( 3 )连接RQ、PQ.
那么点R就是使 的周长最小的点.
老师说,小明的做法正确.接着.老师问同学们,小明这种作法应用了哪些我们学过的定理呢?有四位同学分别说了一个定理,下面的A,B,C,D四个答案分别代表了四个同学所说的定理,其中小明没有应用到的定理是( )
A.如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线
B.等腰三角形底边上的高也是顶角的角平分线
C.线段垂直平分线上的点到线段两个端点的距离相等
D.两点之间,线段最短
3.已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( ).
A.30° B.45° C.60° D.90°
4.如图,牧童在A处放牛,其家在B处,A,B到海岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )
A.750 米 B.1500米 C.500 米 D.1000米
5.如图, 直线 与 轴、 轴分别交于点 和点 ,点 、 分别为线段 、 的中点, 点 为 上一动点, 当 最小时, 点 的坐标为
A. B. C. , D. ,
二、填空题
6.如图,在平面直角坐标系中,O为坐标原点,,点B在y轴上运动,以为边作等腰,(点A,B,C按照顺时针排列),当点B在y轴上运动时,点C也随之运动.在点C的运动过程中,的最小值为 .
三、解答题
7.如图要在燃气管道l上修建一个泵站,分别向A,B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律?
聪明的小明通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线图(2)问题就转化为要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点 ;
②连接 交直线l于点P,则点P即为所求.
请你参考小明的做法解决下列问题:
如图(3),在 ABC中,D,E分别是AB,AC边的中点,请你在BC边上确定一点P,使 的周长最小.
四、作图题
8.如图,在平面直角坐标系中,点C的坐标为(-1,5)。
(1)若把△ABC向右平移5个单位,再向下平移3个单位得到△A'B'C',并写出B'的坐标;
(2)在x轴上找一点P,使得PA+PB的值最小,并求最小值。
五、综合题
9.如图,在平面直角坐标系中完成下列各题:(不写作法,保留作图痕迹)
(1)在图一中作出△ABC关于y轴对称的△A1B1C1并写出A1、B1、C1的坐标.
(2)在图二中x轴上画出点P,使PA+PB的值最小.
10.如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.
答案解析部分
1.【答案】B
【解析】【解答】解:∵垂直平分,
∴关于对称,
设交于D,
∴当P和D重合时,的值最小,最小值等于的长,
的最小值是5.
故答案为:B.
【分析】设交于D,当P和D重合时,的值最小,最小值等于的长,再求解即可。
2.【答案】B
【解析】【解答】解:作点Q关于直线l的对称点 ,可得直线l是 的垂直平分线,用到定理为:如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线,故A不符合题意;
由 ,用到的定理为:线段垂直平分线上的点到线段两个端点的距离相等,故C不符合题意;
从而得出QR+PR= +PR
根据两点之间线段最短,可得 的长即为QR+PR的最小值,故D不符合题意;
没有用到B选项定理,故B符合题意.
故答案为:B.
【分析】根据轴对称的性质可得直线l是 的垂直平分线,从而判断A选项;然后得出 ,从而判断C选项;最后根据两点之间线段最短可得 的长即为QR+PR的最小值,从而判断D选项,即可得出结论.
3.【答案】A
【解析】解答:如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=OP=2,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,
∴OC=OD=CD=2,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故选A.
分析:设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=2可求出α的度数.
4.【答案】D
【解析】【解答】解:作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.
由题意:AC=BD,所以A′C=BD,
所以CM=DM,M为CD的中点,
易得△A′CM≌△BDM,
∴A′M=BM
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=2A′M=1000米.
故最短距离是1000米.
故答案为:D.
【分析】根据轴对称的性质和“两点之间线段最短”,连接A′B,得到最短距离为A′B,再根据全等三角形的性质和A到河岸CD的中点的距离为500米,即可求出A'B的值.
5.【答案】C
【解析】【解答】解:(方法一)如图所示
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y= x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= x+4中y=0,则 x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段A
B、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(-3,2),D′(0,-2),
∴有 ,解得: ,
∴直线CD′的解析式为y= ,
令y= 中y=0,则0= 解得:x= ,
∴点P的坐标为 .
故答案为:C.
(方法二)如图所示
连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y= 中x=0,则y=4,
∴点B的坐标为(0,4);
令y= 中y=0,则 =0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为( ).
故答案为:C.
【分析】(方法一)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
(方法二)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,根据三角形中位线定理即可得出点P为线段CD′的中点,由此即可得出点P的坐标.
6.【答案】
【解析】【解答】如图,过点A作直线l⊥x轴,过C,B作CD⊥l于点D,BE⊥l于点E,
∵∠DCA+∠CAD=90°,∠EAB+∠CAD=180°-90°=90°,
∴∠DCA=∠EAB,
又∵∠CDA=∠AEB=90°,AB=AC,
∴ CDA≌ AEB(AAS),
∴BE=AD,
∵,
∴AD=BE=OA=3,
作点A关于CD的对称点A′,连接
,则点
在直线l上,
,
,
∴,
∵在 COA′中,
∴当O,C,A′三点共线时,
有最小值=OA′,此时,OA′=
,
∴最小值=
.
故答案是:
.
【分析】过点A作直线l⊥x轴,过C,B作CD⊥l于点D,BE⊥l于点E,再利用“AAS”证明 CDA≌ AEB可得BE=AD,再作点A关于CD的对称点A′,连接
,则点
在直线l上,
,
,当O,C,A′三点共线时,
有最小值=OA′,此时,OA′=
,即可得到答案。
7.【答案】解:如图所示:
的周长
为 的中位线
,DE为定值
要使 的周长最小
则 的和最小
根据小明的做法,
过点D作关于BC的对称点F,连接EF与线段BC交于P点,
则此时 的和最小,此时 的周长最小.
【解析】【分析】由于DE为定值,只需 的和最小,根据材料提供的方法作图即可,过点D作关于BC的对称点F,连接EF与线段BC交于P点.
8.【答案】(1)解:△A'B'C'如图所示,点B'的坐标为(3,-2);
(2)解:作点A关于x轴的对称点A1,
∴A1的坐标为(-4,-4),
连接BA1,交x轴于点P,则PA+PB=PA1+PB=BA1,点P即为所求.
此时PA+PB的值最小,
最小值=.
【解析】【分析】(1)分别作出A、B、C的对应点A'、B'、C',顺次连接各顶点即可;
(2)作点A关于x轴的对称点A1,连接BA1,交x轴于点P,根据两点之间线段最短,点P即为所求. 把线段BA1放到两直角边分别为5和2个单位长度的直角三角形中,作为斜边,因此BA1即为 PA+PB 的最小值,长度为.
9.【答案】(1)解:如图一所示;
,
由图可知,A1(﹣1,2),B1(﹣3,1),C1(2,﹣1)
(2)解:如图二所示.
【解析】【分析】(1)画出各点关于y轴的对称点,再顺次连接并写出各点坐标即可;(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则点P即为所求点.
10.【答案】(1)解:如图,
过D作DF⊥BC于F,过F作EF⊥AC交CD于P,
则此时,PA+PE的值最小;
点P即为所求
(2)解:如图,过D作DF⊥BC于F,过F作EF⊥AC交CD于P,
则此时,PA+PE的值最小;
PA+PE的最小值=EF,
∵CD是角平分线,∠BAC=90°,
∴DA=DF,
即点A与点F关于CD对称,
∴CF=AC=10,
∵∠ACB=30°,
∴EF= CF=5.
【解析】【分析】(1) 过D作DF⊥BC于F,过F作EF⊥AC交CD于P, 由轴对称的性质可知: 此时PA+PE的值最小,即点P为所求 ;
(2)过D作DF⊥BC于F,过F作EF⊥AC交CD于P,由(1)知此时PA+PE的值最小,由角平分线的性质可得DA=DF,由轴对称的性质可得 CF=AC,再根据直角三角形中30度角所对的直角边等于斜边的一半可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
