第2章 整式的加减 学情分析卷(含答案)2023--2024学年人教版七年级数学上册
文档属性
| 名称 | 第2章 整式的加减 学情分析卷(含答案)2023--2024学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 47.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 23:48:55 | ||
图片预览


文档简介
整式的加减学情分析卷
(原卷+答案)
时间:_____ 满分:120分
1.用式子表示“m的2倍与n的和的平方”正确的是( )
A.2m+n2 B.(m+2n)2
C.(2m+n)2 D.2(m+n)
2.下列各组单项式中,不是同类项的是( )
A.-a2与2a2 B.2与0
C.2ab2与2a2b D.-mn与2nm
3.关于单项式-xy2z3,下列说法正确的是( )
A.系数是1,次数是5
B.系数是-1,次数是6
C.系数是1,次数是6
D.系数是-1,次数是5
4.计算-2(4a-b)的结果是( )
A.-8a-b B.-8a+b
C.-8a+2b D.-8a-2b
5.下列运算正确的是( )
A.6a-2a=4 B.a3-a2=a
C.2ab-ba=ab D.a2b-ab2=0
6.若多项式3x|m|y2+(m+2)x-1是四次三项式,则m的值为( )
A.2 B.-2 C.±2 D.±1
7.下列去括号中正确的是( )
A.-(x-y)=x-y
B.2(x-y)=2x-y
C.-(x-y-z)=-y+z-x
D.-(x+y-z)=-x-y+z
8.已知2a-ab-1=0,则6a-3ab-2的值是( )
A.-5 B.-1 C.-3 D.1
9.如果M=x2+6x+22,N=-x2+6x-3,那么M与N的大小关系是( )
A.M>N B.M<N
C.M=N D.无法确定
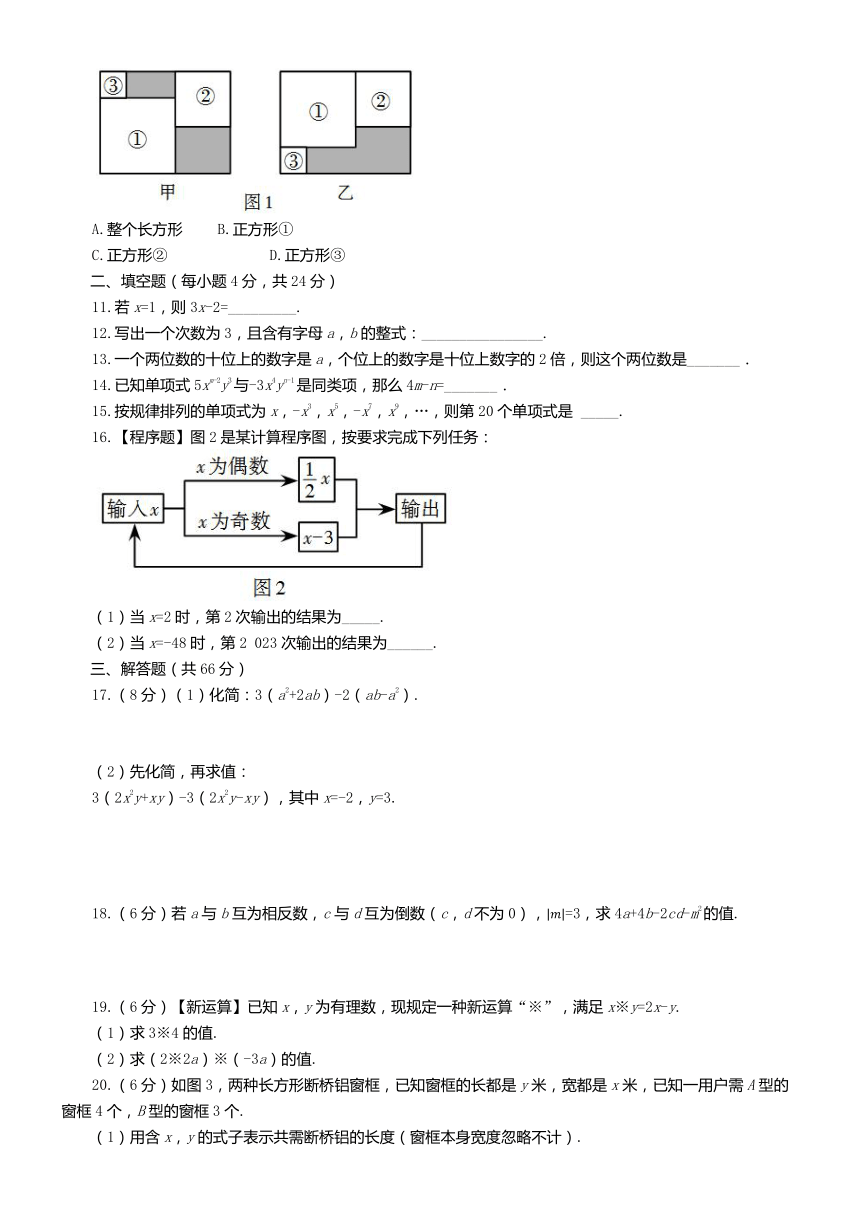
10.三张大小不一的正方形纸片按图1甲和图1乙的方式分别放置于相同的长方形中,它们既不重叠又无空隙,记图1甲中阴影部分的周长之和为m,图1乙中阴影部分的周长为n,要求m与n的差,只需知道一个图形的周长,这个图形是( )
A.整个长方形 B.正方形①
C.正方形② D.正方形③
(每小题4分,共24分)
11.若x=1,则3x-2=_________.
12.写出一个次数为3,且含有字母a,b的整式:________________.
13.一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是_______.
14.已知单项式5xm-2y3与-3x4yn-1是同类项,那么4m-n=_______.
15.按规律排列的单项式为x,-x3,x5,-x7,x9,…,则第20个单项式是 _____.
16.【程序题】图2是某计算程序图,按要求完成下列任务:
(1)当x=2时,第2次输出的结果为_____.
(2)当x=-48时,第2 023次输出的结果为______.
(共66分)
17.(8分)(1)化简:3(a2+2ab)-2(ab-a2).
(2)先化简,再求值:
3(2x2y+xy)-3(2x2y-xy),其中x=-2,y=3.
18.(6分)若a与b互为相反数,c与d互为倒数(c,d不为0),=3,求4a+4b-2cd-m2的值.
19.(6分)【新运算】已知x,y为有理数,现规定一种新运算“※”,满足x※y=2x-y.
(1)求3※4的值.
(2)求(2※2a)※(-3a)的值.
20.(6分)如图3,两种长方形断桥铝窗框,已知窗框的长都是y米,宽都是x米,已知一用户需A型的窗框4个,B型的窗框3个.
(1)用含x,y的式子表示共需断桥铝的长度(窗框本身宽度忽略不计).
(2)若1米断桥铝的平均费用为200元,则当x=1.5,y=2.5时,(1)中断桥铝的总费用为多少元?
21.(8分)如图4,用图案来表示关于a和b的多项式,图案1表示的多项式为4a+b.已知图案中的字母a和b的数量有着一定的规律:
归纳变化规律,解决下列问题:
(1)图案4表示的多项式为___________,图案n表示的多项式为__________(用含n的式子表示).
(2)设图案6表示的多项式为A,图案7表示的多项式为B,化简B-2A.
22.(10分)【探究题】(2023年安徽安庆期中)观察下列等式:
第1个等式:12=13;
第2个等式:(1+2)2=13+23;
第3个等式:(1+2+3)2=13+23+33;
第4个等式:(1+2+3+4)2=13+23+33+43;
……
按照以上规律,解决下列问题:
(1)写出第5个等式:________________.
(2)写出第n(n为正整数)个等式:_______________________________________(用含n的式子表示).
(3)利用你发现的规律计算113+123+133+ +203的值.
23.(10分)已知多项式A=2x2+my-12,B=nx2-3y+6.
(1)若(m+2)2+=0,化简:A-B.
(2)若A+B的结果中不含x2项及y项,求m+n+mn的值.
24.(12分)【新情境】某商家销售一款定价为1 200元的空调和300元的电扇.“五一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一台空调送一台电扇;
方案二:空调和电扇都按定价的90%付款.
现某客户要到该卖场购买空调6台,电扇x台(x>6).
(1)若该客户按方案一购买,则需付款________元;若该客户按方案二购买,则需付款_________元.(用含x的式子表示)
(2)若x=10,通过计算说明此时按哪种方案购买较为合算.
(3)当x=10时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算需付款多少元.
参考答案
一、1.C【提示】m的2倍为2m,与n的和是2m+n,然后平方为(2m+n)2.故选C.
2.C【提示】在2ab2中,a,b的指数分别为1,2,在2a2b中,a,b的指数分别为2,1,相同字母的指数不同,故不是同类项.
3.B【提示】单项式-xy2z3的系数是-1,次数是1+2+3=6.
4.C【提示】-2(4a-b)=-8a+2b.
5.C【提示】A.6a-2a=4a,本选项错误;
B.a3与-a2不是同类项,不能合并,本选项错误;
C.2ab-ba=ab,本选项正确;
D.a2b与-ab2不是同类项,不能合并,本选项错误.
6.A【提示】因为多项式3x|m|y2+(m+2)x-1是四次三项式,所以|m|+2=4且m+2≠0.所以m=2.
7.D【提示】A.-(x-y)=-x+y,本选项错误;
B.2(x-y)=2x-2y,本选项错误;
C.-(x-y-z)=-x+y+z,本选项错误;
D.-(x+y-z)=-x-y+z,本选项正确.
8.D【提示】6a-3ab-2=3(2a-ab-1)+1=0+1=1.
9.A【提示】因为M-N=x2+6x+22-(-x2+6x-3)=x2+6x+22+x2-6x+3=2x2+25.
又因为x2≥0,所以2x2+25>0.所以M>N.
10.D【提示】设正方形①的边长为a,正方形②的边长为b,正方形③的边长为c,则m=2(a-c)+2b+2c+2(a+c-b)=4a+2c;n=2(a+b-c)+2(a+c-b)=4a.
所以m-n=4a+2c-4a=2c.故选D.
二、11.1【提示】当x=1时,3x-2=3-2=1.
12.a2b(答案不唯一)【提示】答案不唯一.如a2b.
13.12a【提示】由十位上的数字是a,个位上的数字是十位上数字的2倍,则个位上的数字是2a.
所以这个两位数是10a+2a=12a.
14.20【提示】由已知,得m-2=4,n-1=3.
所以m=6,n=4.所以4m-n=4×6-4=24-4=20.
15.-x39 【提示】根据前几项可以得出规律,奇数项为正,偶数项为负,第n个单项式为(-1)n+1·x2n-1,则第20个单项式是(-1)21×x39=-x39.
16.(1)-2 (2)-6【提示】(1)当x=2时,第1次输出的结果为1;第2次输出的结果为-2.
(2)当x=-48时,
第1次输出的结果为-24;
第2次输出的结果为-12;
第3次输出的结果为-6;
第4次输出的结果为-3;
第5次输出的结果为-6;
……
所以从第3次开始,第奇数次输出的结果为-6,第偶数次输出的结果为-3.
所以第2 023次输出的结果为-6.
三、17.(1)原式=3a2+6ab-2ab+2a2=5a2+4ab.
(2)原式=6x2y+3xy-6x2y+3xy=6xy.
当x=-2,y=3时,原式=6×(-2)×3=-36.
18.根据题意,得a+b=0,cd=1,m2=9.
原式=4(a+b)-2cd-m2=4×0-2×1-9=0-2-9=-11.
19.(1)3※4=2×3-4=6-4=2.
(2)2※2a=2×2-2a=4-2a,
(4-2a)※(-3a)=2(4-2a)-(-3a)=8-4a+3a=8-a.
20.(1)由题意,得4(3x+2y)+3(2x+2y)=18x+14y.
所以共需断桥铝的长度为(18x+14y)米.
(2)当x=1.5,y=2.5时,
18x+14y=18×1.5+14×2.5=27+35=62,
200×62=12 400(元).
所以(1)中断桥铝的总费用为12 400元.
21.(1)图案4表示的多项式为25a+16b,图案n表示的多项式为(n+1)2a+n2b.
故分别填25a+16b;(n+1)2a+n2b.
(2)因为A=49a+36b,B=64a+49b,
所以B-2A=64a+49b-2(49a+36b)
=64a+49b-98a-72b
=-34a-23b.
22.(1)(1+2+3+4+5)2=13+23+33+43+53.
(2)(1+2+3+4+5+…+n)2=13+23+33+43+53+…+n3.
(3)113+123+133+…+203
=13+23+33+43+53+…+203-(13+23+33+43+53+…+103)
=(1+2+3+…+20)2-(1+2+3+…+10)2
=2102-552
=41 075.
23.(1)A-B=(2x2+my-12)-(nx2-3y+6)
=2x2+my-12-nx2+3y-6
=(2-n)x2+(m+3)y-18.
因为(m+2)2+|n-3|=0,
所以m+2=0,n-3=0.
所以m=-2,n=3.
所以原式=-x2+y-18.
(2)A+B=(2x2+my-12)+(nx2-3y+6)
=2x2+my-12+nx2-3y+6
=(n+2)x2+(m-3)y-6.
因为A+B的结果中不含x2项及y项,
所以n+2=0,m-3=0.
所以m=3,n=-2.
所以m+n+mn=3-2+3×(-2)=1-6=-5.
24.(1)按方案一购买,需付款:
1 200×6+300(x-6)=(5 400+300x)元;
按方案二购买,需付款:
1 200×6×90%+300x×90%=(6 480+270x)元.
故分别填(5 400+300x);(6 480+270x).
(2)当x=10时,
方案一:5 400+300×10=8 400(元),
方案二:6 480+270×10=9 180(元).
因为8 400<9 180,
所以此时按方案一购买较为合算.
(3)先按方案一买6台空调,送6台电扇,再按方案二买4台电扇,需付款:
6×1 200+4×300×90%=8 280(元).
答:先按方案一买6台空调,再按方案二买4台电扇更为省钱;需付款8 280元.
(原卷+答案)
时间:_____ 满分:120分
1.用式子表示“m的2倍与n的和的平方”正确的是( )
A.2m+n2 B.(m+2n)2
C.(2m+n)2 D.2(m+n)
2.下列各组单项式中,不是同类项的是( )
A.-a2与2a2 B.2与0
C.2ab2与2a2b D.-mn与2nm
3.关于单项式-xy2z3,下列说法正确的是( )
A.系数是1,次数是5
B.系数是-1,次数是6
C.系数是1,次数是6
D.系数是-1,次数是5
4.计算-2(4a-b)的结果是( )
A.-8a-b B.-8a+b
C.-8a+2b D.-8a-2b
5.下列运算正确的是( )
A.6a-2a=4 B.a3-a2=a
C.2ab-ba=ab D.a2b-ab2=0
6.若多项式3x|m|y2+(m+2)x-1是四次三项式,则m的值为( )
A.2 B.-2 C.±2 D.±1
7.下列去括号中正确的是( )
A.-(x-y)=x-y
B.2(x-y)=2x-y
C.-(x-y-z)=-y+z-x
D.-(x+y-z)=-x-y+z
8.已知2a-ab-1=0,则6a-3ab-2的值是( )
A.-5 B.-1 C.-3 D.1
9.如果M=x2+6x+22,N=-x2+6x-3,那么M与N的大小关系是( )
A.M>N B.M<N
C.M=N D.无法确定
10.三张大小不一的正方形纸片按图1甲和图1乙的方式分别放置于相同的长方形中,它们既不重叠又无空隙,记图1甲中阴影部分的周长之和为m,图1乙中阴影部分的周长为n,要求m与n的差,只需知道一个图形的周长,这个图形是( )
A.整个长方形 B.正方形①
C.正方形② D.正方形③
(每小题4分,共24分)
11.若x=1,则3x-2=_________.
12.写出一个次数为3,且含有字母a,b的整式:________________.
13.一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是_______.
14.已知单项式5xm-2y3与-3x4yn-1是同类项,那么4m-n=_______.
15.按规律排列的单项式为x,-x3,x5,-x7,x9,…,则第20个单项式是 _____.
16.【程序题】图2是某计算程序图,按要求完成下列任务:
(1)当x=2时,第2次输出的结果为_____.
(2)当x=-48时,第2 023次输出的结果为______.
(共66分)
17.(8分)(1)化简:3(a2+2ab)-2(ab-a2).
(2)先化简,再求值:
3(2x2y+xy)-3(2x2y-xy),其中x=-2,y=3.
18.(6分)若a与b互为相反数,c与d互为倒数(c,d不为0),=3,求4a+4b-2cd-m2的值.
19.(6分)【新运算】已知x,y为有理数,现规定一种新运算“※”,满足x※y=2x-y.
(1)求3※4的值.
(2)求(2※2a)※(-3a)的值.
20.(6分)如图3,两种长方形断桥铝窗框,已知窗框的长都是y米,宽都是x米,已知一用户需A型的窗框4个,B型的窗框3个.
(1)用含x,y的式子表示共需断桥铝的长度(窗框本身宽度忽略不计).
(2)若1米断桥铝的平均费用为200元,则当x=1.5,y=2.5时,(1)中断桥铝的总费用为多少元?
21.(8分)如图4,用图案来表示关于a和b的多项式,图案1表示的多项式为4a+b.已知图案中的字母a和b的数量有着一定的规律:
归纳变化规律,解决下列问题:
(1)图案4表示的多项式为___________,图案n表示的多项式为__________(用含n的式子表示).
(2)设图案6表示的多项式为A,图案7表示的多项式为B,化简B-2A.
22.(10分)【探究题】(2023年安徽安庆期中)观察下列等式:
第1个等式:12=13;
第2个等式:(1+2)2=13+23;
第3个等式:(1+2+3)2=13+23+33;
第4个等式:(1+2+3+4)2=13+23+33+43;
……
按照以上规律,解决下列问题:
(1)写出第5个等式:________________.
(2)写出第n(n为正整数)个等式:_______________________________________(用含n的式子表示).
(3)利用你发现的规律计算113+123+133+ +203的值.
23.(10分)已知多项式A=2x2+my-12,B=nx2-3y+6.
(1)若(m+2)2+=0,化简:A-B.
(2)若A+B的结果中不含x2项及y项,求m+n+mn的值.
24.(12分)【新情境】某商家销售一款定价为1 200元的空调和300元的电扇.“五一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一台空调送一台电扇;
方案二:空调和电扇都按定价的90%付款.
现某客户要到该卖场购买空调6台,电扇x台(x>6).
(1)若该客户按方案一购买,则需付款________元;若该客户按方案二购买,则需付款_________元.(用含x的式子表示)
(2)若x=10,通过计算说明此时按哪种方案购买较为合算.
(3)当x=10时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算需付款多少元.
参考答案
一、1.C【提示】m的2倍为2m,与n的和是2m+n,然后平方为(2m+n)2.故选C.
2.C【提示】在2ab2中,a,b的指数分别为1,2,在2a2b中,a,b的指数分别为2,1,相同字母的指数不同,故不是同类项.
3.B【提示】单项式-xy2z3的系数是-1,次数是1+2+3=6.
4.C【提示】-2(4a-b)=-8a+2b.
5.C【提示】A.6a-2a=4a,本选项错误;
B.a3与-a2不是同类项,不能合并,本选项错误;
C.2ab-ba=ab,本选项正确;
D.a2b与-ab2不是同类项,不能合并,本选项错误.
6.A【提示】因为多项式3x|m|y2+(m+2)x-1是四次三项式,所以|m|+2=4且m+2≠0.所以m=2.
7.D【提示】A.-(x-y)=-x+y,本选项错误;
B.2(x-y)=2x-2y,本选项错误;
C.-(x-y-z)=-x+y+z,本选项错误;
D.-(x+y-z)=-x-y+z,本选项正确.
8.D【提示】6a-3ab-2=3(2a-ab-1)+1=0+1=1.
9.A【提示】因为M-N=x2+6x+22-(-x2+6x-3)=x2+6x+22+x2-6x+3=2x2+25.
又因为x2≥0,所以2x2+25>0.所以M>N.
10.D【提示】设正方形①的边长为a,正方形②的边长为b,正方形③的边长为c,则m=2(a-c)+2b+2c+2(a+c-b)=4a+2c;n=2(a+b-c)+2(a+c-b)=4a.
所以m-n=4a+2c-4a=2c.故选D.
二、11.1【提示】当x=1时,3x-2=3-2=1.
12.a2b(答案不唯一)【提示】答案不唯一.如a2b.
13.12a【提示】由十位上的数字是a,个位上的数字是十位上数字的2倍,则个位上的数字是2a.
所以这个两位数是10a+2a=12a.
14.20【提示】由已知,得m-2=4,n-1=3.
所以m=6,n=4.所以4m-n=4×6-4=24-4=20.
15.-x39 【提示】根据前几项可以得出规律,奇数项为正,偶数项为负,第n个单项式为(-1)n+1·x2n-1,则第20个单项式是(-1)21×x39=-x39.
16.(1)-2 (2)-6【提示】(1)当x=2时,第1次输出的结果为1;第2次输出的结果为-2.
(2)当x=-48时,
第1次输出的结果为-24;
第2次输出的结果为-12;
第3次输出的结果为-6;
第4次输出的结果为-3;
第5次输出的结果为-6;
……
所以从第3次开始,第奇数次输出的结果为-6,第偶数次输出的结果为-3.
所以第2 023次输出的结果为-6.
三、17.(1)原式=3a2+6ab-2ab+2a2=5a2+4ab.
(2)原式=6x2y+3xy-6x2y+3xy=6xy.
当x=-2,y=3时,原式=6×(-2)×3=-36.
18.根据题意,得a+b=0,cd=1,m2=9.
原式=4(a+b)-2cd-m2=4×0-2×1-9=0-2-9=-11.
19.(1)3※4=2×3-4=6-4=2.
(2)2※2a=2×2-2a=4-2a,
(4-2a)※(-3a)=2(4-2a)-(-3a)=8-4a+3a=8-a.
20.(1)由题意,得4(3x+2y)+3(2x+2y)=18x+14y.
所以共需断桥铝的长度为(18x+14y)米.
(2)当x=1.5,y=2.5时,
18x+14y=18×1.5+14×2.5=27+35=62,
200×62=12 400(元).
所以(1)中断桥铝的总费用为12 400元.
21.(1)图案4表示的多项式为25a+16b,图案n表示的多项式为(n+1)2a+n2b.
故分别填25a+16b;(n+1)2a+n2b.
(2)因为A=49a+36b,B=64a+49b,
所以B-2A=64a+49b-2(49a+36b)
=64a+49b-98a-72b
=-34a-23b.
22.(1)(1+2+3+4+5)2=13+23+33+43+53.
(2)(1+2+3+4+5+…+n)2=13+23+33+43+53+…+n3.
(3)113+123+133+…+203
=13+23+33+43+53+…+203-(13+23+33+43+53+…+103)
=(1+2+3+…+20)2-(1+2+3+…+10)2
=2102-552
=41 075.
23.(1)A-B=(2x2+my-12)-(nx2-3y+6)
=2x2+my-12-nx2+3y-6
=(2-n)x2+(m+3)y-18.
因为(m+2)2+|n-3|=0,
所以m+2=0,n-3=0.
所以m=-2,n=3.
所以原式=-x2+y-18.
(2)A+B=(2x2+my-12)+(nx2-3y+6)
=2x2+my-12+nx2-3y+6
=(n+2)x2+(m-3)y-6.
因为A+B的结果中不含x2项及y项,
所以n+2=0,m-3=0.
所以m=3,n=-2.
所以m+n+mn=3-2+3×(-2)=1-6=-5.
24.(1)按方案一购买,需付款:
1 200×6+300(x-6)=(5 400+300x)元;
按方案二购买,需付款:
1 200×6×90%+300x×90%=(6 480+270x)元.
故分别填(5 400+300x);(6 480+270x).
(2)当x=10时,
方案一:5 400+300×10=8 400(元),
方案二:6 480+270×10=9 180(元).
因为8 400<9 180,
所以此时按方案一购买较为合算.
(3)先按方案一买6台空调,送6台电扇,再按方案二买4台电扇,需付款:
6×1 200+4×300×90%=8 280(元).
答:先按方案一买6台空调,再按方案二买4台电扇更为省钱;需付款8 280元.
