23.1 图形的旋转 提升练习(含解析)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 23.1 图形的旋转 提升练习(含解析)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 758.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 23:48:16 | ||
图片预览


文档简介
23.1 图形的旋转(提升练习)
一.选择题
1.下列图形分别绕某个点旋转120°后不能与自身重合的是( )
A. B. C. D.
2.在平面直角坐标系中,将点P(4,3)绕原点旋转180°后,得到对应点Q的坐标是( )
A.(4,﹣3) B.(﹣4,3) C.(3,4) D.(﹣4,﹣3)
3.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB=CB′,则∠C′的度数为( )
A.18° B.20° C.24° D.28°
4.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
5.如图,将平行四边形ABCD绕点A逆时针旋转到平行四边形A′B′C′D′的位置,使点B'落在BC上,B′C′与CD交于点E,若AB=3,BC=4,BB′=1,则CE的长为( )
A. B. C. D.1
6.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.则下列结论不正确的是( )
A.∠EAF=45° B.△EBF为等腰直角三角形
C.AE平分∠DAF D.BE+CD>ED
第3题图 第4题图 第5题图 第6题图
7.如图,在4×4的正方形网格中,△MPN绕某点旋转一定的角度,得到△M'P'N',其旋转中心是( )
A.点A B.点B C.点C D.点D
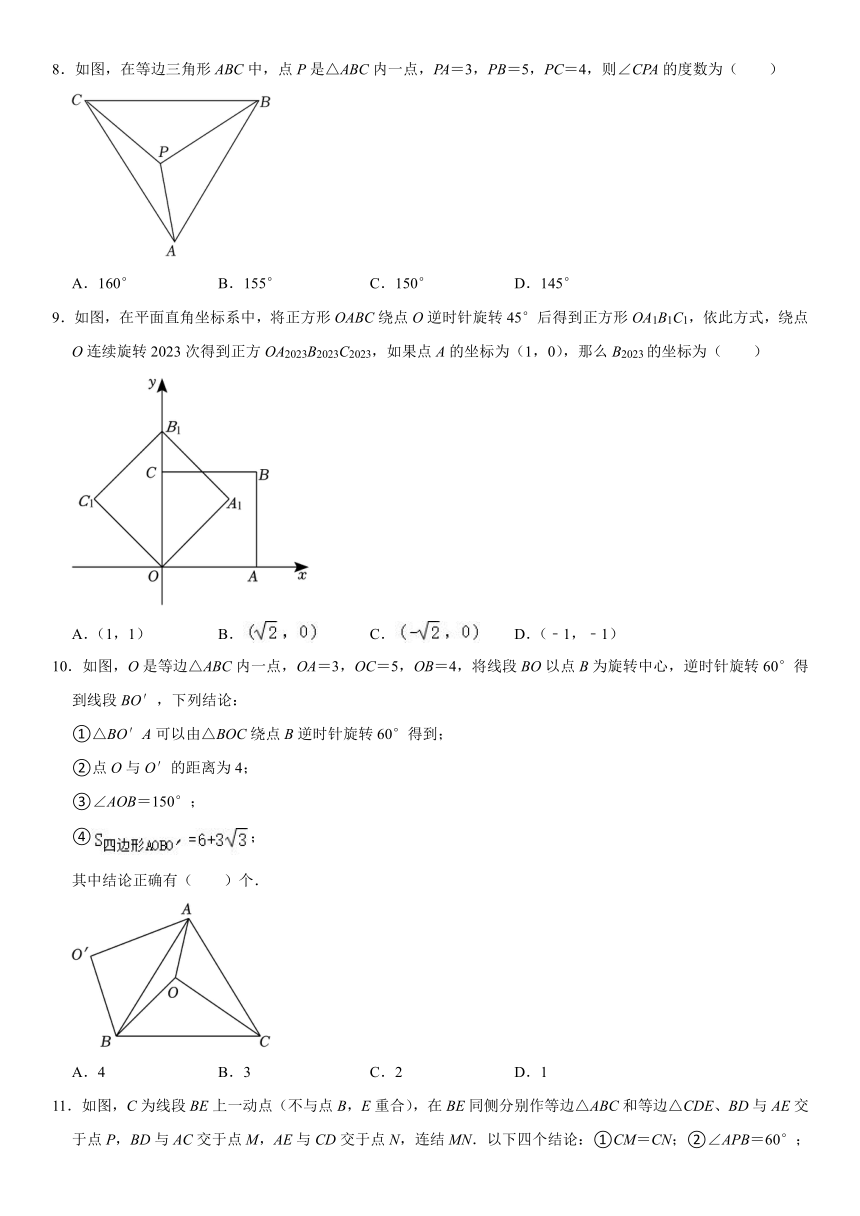
8.如图,在等边三角形ABC中,点P是△ABC内一点,PA=3,PB=5,PC=4,则∠CPA的度数为( )
A.160° B.155° C.150° D.145°
9.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2023次得到正方OA2023B2023C2023,如果点A的坐标为(1,0),那么B2023的坐标为( )
A.(1,1) B. C. D.(﹣1,﹣1)
10.如图,O是等边△ABC内一点,OA=3,OC=5,OB=4,将线段BO以点B为旋转中心,逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④;
其中结论正确有( )个.
A.4 B.3 C.2 D.1
11.如图,C为线段BE上一动点(不与点B,E重合),在BE同侧分别作等边△ABC和等边△CDE、BD与AE交于点P,BD与AC交于点M,AE与CD交于点N,连结MN.以下四个结论:①CM=CN;②∠APB=60°;③PA+PC=PB;④PC平分∠BPE,恒成立的结论有( )
A.①②④ B.①②③④ C.①③④ D.①④
12.如图,已知△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转n°(0<n<∠BAC)得到△ADE,AD交于点F,DE交BC,AC于点G,H,则以下结论:
①△ABF≌△AEH;
②连接AG,FH,则AG⊥FH;
③当AD⊥BC时,DF的长度最大;
④当H点是DE的中点时,四边形AFGH的面积等于AF×GH.
其中正确的个数有( )
A.4个 B.3个 C.5个 D.1个
二.填空题
13.如图,在等腰△ABC中,AB=AC,∠C=25°,将△ABC绕点B逆时针旋转至△DBE且点A的对应点D落在CA延长线上,则∠CBE= .
14.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:
①OD=OE;
②S△ODE=S△BDE;
③四边形ODBE的面积始终等于;
④△BDE周长的最小值为6.
上述结论中正确的有 (写出序号).
15.如图,在平面直角坐标系中,点B的坐标是(﹣3,2),OA=1,将点B绕点A顺时针旋转90°得到点C,则点C的坐标是 .
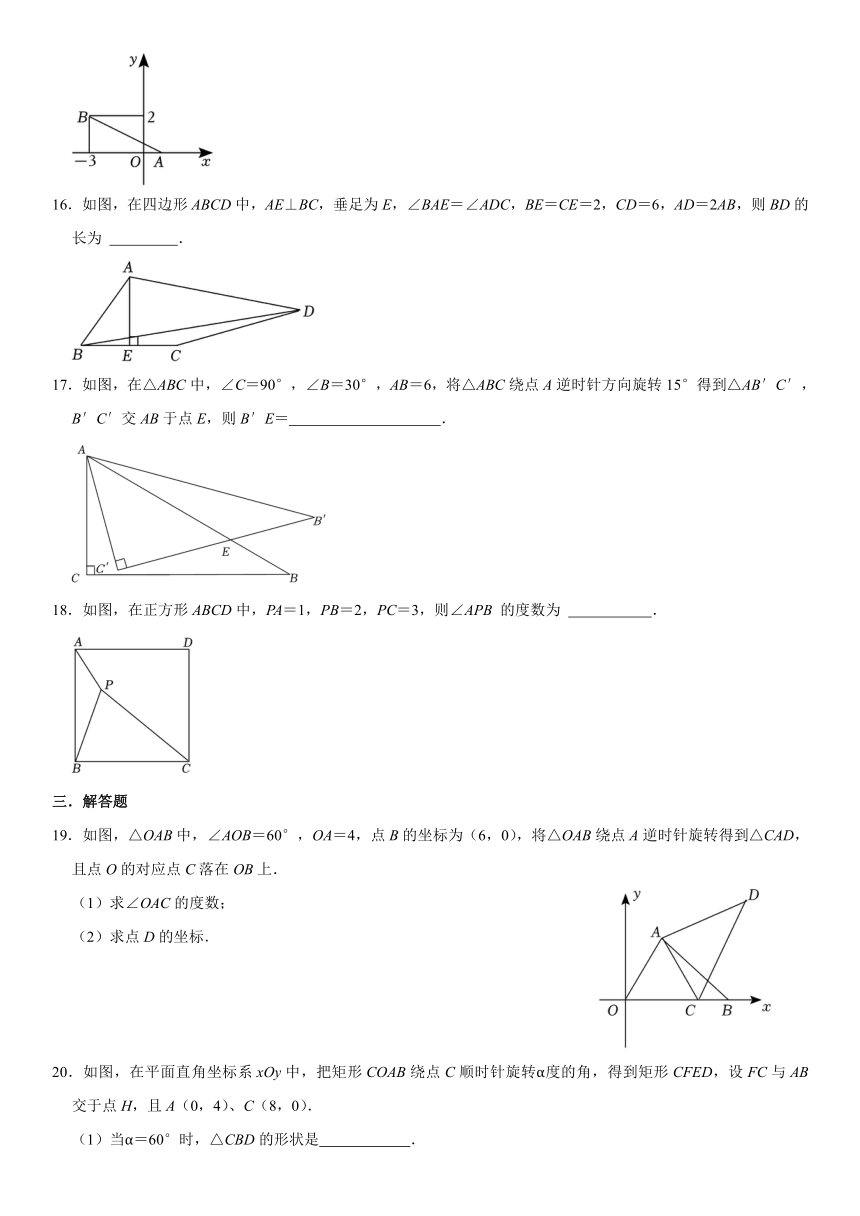
16.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=6,AD=2AB,则BD的长为 .
17.如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
18.如图,在正方形ABCD中,PA=1,PB=2,PC=3,则∠APB 的度数为 .
三.解答题
19.如图,△OAB中,∠AOB=60°,OA=4,点B的坐标为(6,0),将△OAB绕点A逆时针旋转得到△CAD,且点O的对应点C落在OB上.
(1)求∠OAC的度数;
(2)求点D的坐标.
20.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α度的角,得到矩形CFED,设FC与AB交于点H,且A(0,4)、C(8,0).
(1)当α=60°时,△CBD的形状是 .
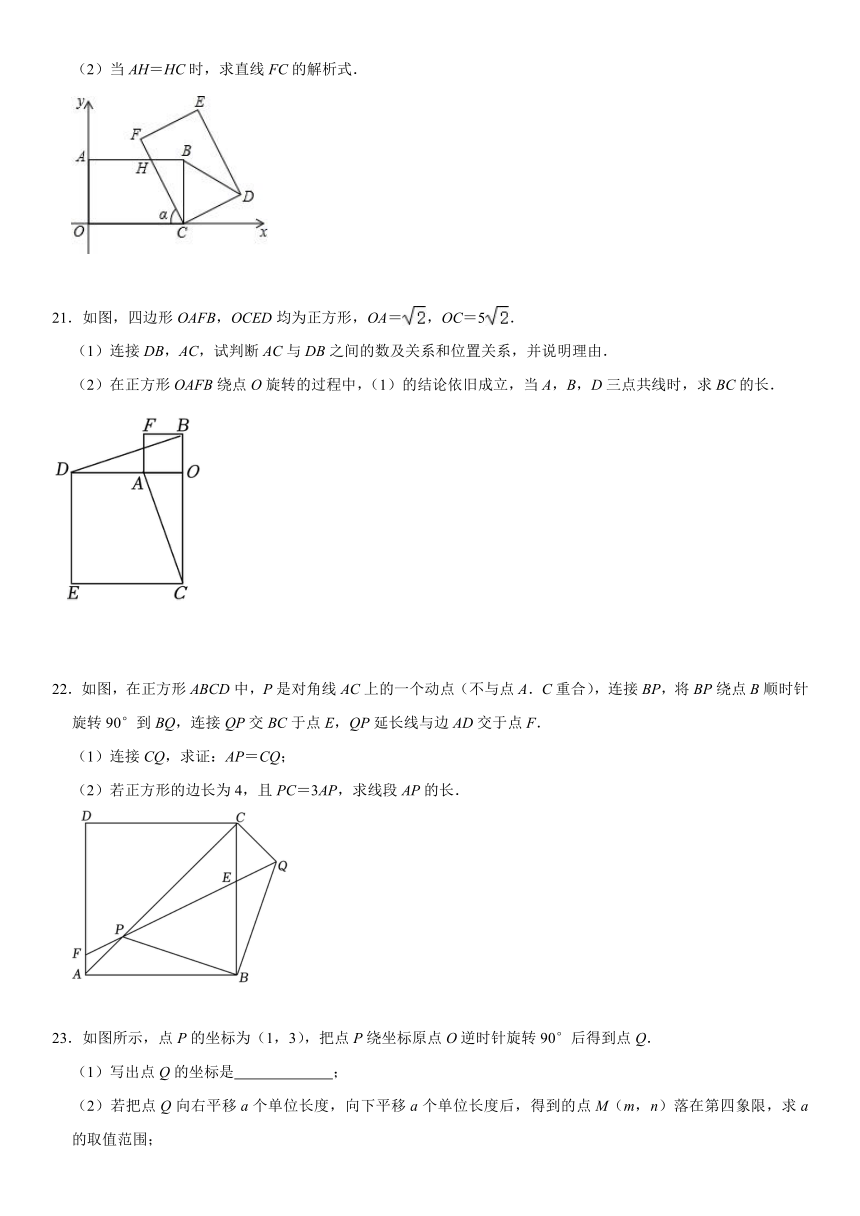
(2)当AH=HC时,求直线FC的解析式.
21.如图,四边形OAFB,OCED均为正方形,OA=,OC=5.
(1)连接DB,AC,试判断AC与DB之间的数及关系和位置关系,并说明理由.
(2)在正方形OAFB绕点O旋转的过程中,(1)的结论依旧成立,当A,B,D三点共线时,求BC的长.
22.如图,在正方形ABCD中,P是对角线AC上的一个动点(不与点A.C重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP交BC于点E,QP延长线与边AD交于点F.
(1)连接CQ,求证:AP=CQ;
(2)若正方形的边长为4,且PC=3AP,求线段AP的长.
23.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 ;
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围;
(3)在(2)条件下,当a取何值,代数式m2+2n+5取得最小值.
24.如图1,在△ABC中,BA=BC,D、E是AC边上的两点,且满足∠DBE=∠ABC.以点B为旋转中心,将△CBE按逆时针方向旋转得到△ABF,连接DF.
(1)求证:DF=DE;
(2)如图2,若AB⊥BC,其他条件不变.求证:DE2=AD2+EC2.
25.如图,四边形ABCD是正方形,连接AC,将△ABC绕点A逆时针旋转α得△AEF,连接CF,O为CF的中点,连接OE,OD.
(1)如图1,当α=45°时,求证:OE=OD;
(2)如图2,当45°<α<90°时,(1)OE=OD还成立吗?请说明理由.
26.如图,将一个含45°角的三角尺的直角顶点放在点M(8,8)处,三角尺的两边分别交x轴、y轴的正半轴于A,B两点.
(1)求OA+OB的值;
(2)把三角尺绕点M旋转,在旋转的过程中保持AP平分∠OAB,AP交OM于P,PN⊥x轴于N.下列两个结论:①PN+AB的值不变;②PN+AB的值不变,其中只有一个正确,请选择正确的结论,直接写出其值.
27.如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM+CN=BD.
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?
若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
28.如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为a.
(1)当点D′恰好落在EF边上时,求旋转角a的值;
(2)如图2,G为BC中点,且0°<a<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角a的值;若不能说明理由.
23.1 图形的旋转(提升练习)
一.选择题
1.下列图形分别绕某个点旋转120°后不能与自身重合的是( )
A. B. C. D.
【解答】解:A、等边三角形绕它的中心旋转120°能与本身重合,本选项不符合题意.
B、圆绕圆心旋转任意角度能与本身重合,本选项不符合题意.
C、这个图形绕中心性质120°能与本身重合,本选项不符合题意.
D、五角星绕中心旋转72°与本身重合,本选项符合题意.
故选:D.
2.在平面直角坐标系中,将点P(4,3)绕原点旋转180°后,得到对应点Q的坐标是( )
A.(4,﹣3) B.(﹣4,3) C.(3,4) D.(﹣4,﹣3)
【解答】解:∵将点P(4,3)绕原点O旋转180°后,得到的对应点Q,
∴点Q和点P关于原点对称,
∵点P的坐标为(4,3),
∴点Q的坐标是(﹣4,﹣3).
故选:D.
3.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB=CB′,则∠C′的度数为( )
A.18° B.20° C.24° D.28°
【解答】解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣108°,
∴∠C=24°,
∴∠C'=∠C=24°,
故选:C.
4.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
【解答】解:如图,过点A作AE⊥OB于E,过点A′作A′H⊥x轴于H.
∵B(2,0),△AOB是等边三角形,
∴OA=OB=AB=2,
∵AE⊥OB,
∴OE=EB=1,
∴AE===,
∵A′H⊥OH,
∴∠A′HO=∠AEO=∠AOA′=90°,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(﹣,1),
故选:C.
5.如图,将平行四边形ABCD绕点A逆时针旋转到平行四边形A′B′C′D′的位置,使点B'落在BC上,B′C′与CD交于点E,若AB=3,BC=4,BB′=1,则CE的长为( )
A. B. C. D.1
【解答】解:如图,连接DD',
由旋转可知,∠BAB′=∠DAD′,AB′=AB=3,AD′=AD=4,
∴△BAB′∽△DAD′,
∴AB:BB′=AD:DD′=3:1,∠AD′D=∠AB′B=∠B,
∴DD′=,
又∵∠AD′C′=∠AB′C′=∠B,∠AD′D=∠B=∠AB′B,
∴∠AD′C′=∠AD′D,即点D′,D,C′在同一条直线上,
∴DC′=,
又∠C′=∠ECB′,∠DEC′=∠B′EC,
∴△CEB′∽△C'ED,
∴B′E:DE=CE:C′E=B′C:DC′,即B′E:DE=CE:C′E=3:,
设CE=x,B'E=y,
∴x:(4﹣y)=y:(3﹣x)=3:,
∴x=,
∴CE=,
故选:A.
6.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.则下列结论不正确的是( )
A.∠EAF=45° B.△EBF为等腰直角三角形
C.AE平分∠DAF D.BE+CD>ED
【解答】解:∵△ADC绕点A顺时针旋转90°后,得到△AFB,
∴△ADC≌△AFB,∠FAD=90°,AD=AF,BF=CD,
∵∠DAE=45°,
∴∠EAF=90°﹣∠DAE=45°,所以A正确,不符合题意;
∴∠DAE=∠EAF,
∴AE平分∠DAF,所以C正确,不符合题意;
,
∴△AED≌△AEF(SAS),
∴ED=EF,
∵BE+BF>EF,
∴BE+CD>ED,
所以D正确,不符合题意;
在Rt△ABC中,AB=AC,
∴∠ABC=∠ACB=45°,
∵△ADC≌△AFB,
∴∠ACD=∠ABF=45°,
∵∠ABF+∠ABE=∠ACD+∠ABC=90°,
∴△EBF为直角三角形,
但是BE、CD不一定相等,所以BE、BF不一定相等,所以B不正确,符合题意.
故选:B.
7.如图,在4×4的正方形网格中,△MPN绕某点旋转一定的角度,得到△M'P'N',其旋转中心是( )
A.点A B.点B C.点C D.点D
【解答】解:如图,由旋转可知:P和P'为对应点,N和N'为对应点,
连接PP'、NN',作PP'、NN'的垂直平分线,
可得:点B为旋转中心,
故选:B.
8.如图,在等边三角形ABC中,点P是△ABC内一点,PA=3,PB=5,PC=4,则∠CPA的度数为( )
A.160° B.155° C.150° D.145°
【解答】解:如图,将△ACP绕点A顺时针旋转60°,得到△ABE,连接PE,
∴△ACP≌△ABE,∠PAE=60°,
∴AP=AE=3,CP=BE=4,∠AEB=∠APC,
∴△PAE是等边三角形,
∴PE=AE=3,∠AEP=60°,
∵PB2=25,PE2+BE2=9+16=25,
∴PB2=PE2+BE2,
∴∠PEB=90°,
∴∠AEB=150°=∠APC,
故选:C.
9.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2023次得到正方OA2023B2023C2023,如果点A的坐标为(1,0),那么B2023的坐标为( )
A.(1,1) B. C. D.(﹣1,﹣1)
【解答】解:∵点A的坐标为(1,0),
∴OA=1,
∵四边形OABC是正方形,
∴∠OAB=90°,AB=OA=1,
∴B(2,2),
连接OB,如图:
由勾股定理得:,
由旋转的性质得:,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴,B2(﹣1,1),,B4(﹣1,﹣1),,B6(1,﹣1),,…,
发现是8次一循环,则2023÷8=252…7,
∴点B2023的坐标为,
故选:B.
10.如图,O是等边△ABC内一点,OA=3,OC=5,OB=4,将线段BO以点B为旋转中心,逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④;
其中结论正确有( )个.
A.4 B.3 C.2 D.1
【解答】解:连接OO′,
∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC,
∵将线段BO以点B为旋转中心,逆时针旋转60°得到线段BO′,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到;
故①是正确的;
∵OB=OB,∠OBO′=60°,
∴△O′BO是等边三角形,
∴OO′=OB=4,
故②是正确的;
∵△O′BO是等边三角形,
∴∠O′OB=60°,
∵OO′=OB=4,AO=3,AO′=OC=5,
∴∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=150°,
故③是正确的;
④S四边形AOBO′=S△AOO′+S△OO′B=(4×4×+4×3)=4+6,
故③是错误的,
故选:B.
11.如图,C为线段BE上一动点(不与点B,E重合),在BE同侧分别作等边△ABC和等边△CDE、BD与AE交于点P,BD与AC交于点M,AE与CD交于点N,连结MN.以下四个结论:①CM=CN;②∠APB=60°;③PA+PC=PB;④PC平分∠BPE,恒成立的结论有( )
A.①②④ B.①②③④ C.①③④ D.①④
【解答】解:∵△ABC和△DCE都为等边三角形,
∴CA=CB,∠ACB=60°,CD=CE,∠DCE=60°,
∴∠BCD=∠ACE=120°,
在△BCD和△ACE中,
,
∴△BCD≌△ACE(SAS),
∴∠CBD=∠CAE,
∵∠AMP=∠CMB,
∴∠APM=∠BCM=60°,
即∠APB=60°,所以②正确;
∵∠ACB=∠DCE=60°,
∴∠ACN=60°,
在△BCM和△ACN中,
,
∴△BCM≌△ACN(ASA),
∴CM=CN,所以①正确;
过C点作CH⊥BD于H点,CQ⊥AE于Q点,如图,
∵△BCD≌△ACE,
∴CH=CQ,
∴PC平分∠BPE,所以④正确;
∵∠APB=60°,
∴∠BPE=120°,
∴∠BPC=60°,
在PB上截取PG=PC,如图,则△PCG为等边三角形,
∴CG=PG=PC,∠PGC=60°,
∵∠APC=∠APB+∠BPC=120°,∠BGC=180°﹣∠PGC=120°,
∴∠APC=∠BGC,
在△BCG和△ACP中,
,
∴△BCG≌△ACP(AAS),
∴BG=AP,
∴PA+PC=BG+PG=PB,所以③正确.
故选:B.
12.如图,已知△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转n°(0<n<∠BAC)得到△ADE,AD交于点F,DE交BC,AC于点G,H,则以下结论:
①△ABF≌△AEH;
②连接AG,FH,则AG⊥FH;
③当AD⊥BC时,DF的长度最大;
④当H点是DE的中点时,四边形AFGH的面积等于AF×GH.
其中正确的个数有( )
A.4个 B.3个 C.5个 D.1个
【解答】解:①∵AB=AC,
∴∠B=∠C,
由旋转得AB=AC=AE,∠BAF=∠HAE,∠B=∠C=∠E,
∴△ABF≌△AEH(ASA),故①正确;
②连接AG、FH,
∵△ABF≌△AEH,
∴∠AFB=∠AHE,AF=AH,
∵∠AFB=∠DFG,∠AHE=∠CHG,
∴∠DFG=∠CHG,
∵AD=AB=AC,∴DF=CH,
又∵∠DGF=∠CGH,
∴△DFG≌△CHG(AAS),
∴FG=GH,
∴AG垂直平分FH,故②正确;
③∵DF=AD﹣AF,AD是定长,
∴AF最小时,DF最长,
∴AD⊥BC时,DF的长度最大,故③正确;
④∵AD=AE,
∴当点H是DE的中点时,有AH⊥DE,
∵AF=AH,FG=GH,AG=AG,
∴△AFG≌△AHG(SSS),
∴S四边形AFGH=2S△AGH=2×GH×AH=GH×AF,故④正确.
故选:A.
二.填空题
13.如图,在等腰△ABC中,AB=AC,∠C=25°,将△ABC绕点B逆时针旋转至△DBE且点A的对应点D落在CA延长线上,则∠CBE= 80° .
【解答】解:∵AB=AC,
∴∠C=∠ABC=25°,
∴∠BAD=50°,
∵将△ABC绕点B逆时针旋转至△DBE,
∴AB=BD,∠ABC=∠DBE=25°,∠CBE=∠DBE,
∴∠BDA=∠BAD=50°,
∴∠DBA=80°,
∴∠CBE=∠DBE=80°,
故答案为:80°.
14.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:
①OD=OE;
②S△ODE=S△BDE;
③四边形ODBE的面积始终等于;
④△BDE周长的最小值为6.
上述结论中正确的有 ①③④ (写出序号).
【解答】解:连接OB、OC,如图,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O是△ABC的中心,
∴OB=OC,OB、OC分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=∠OCB=30°,
∴∠BOC=120°,即∠BOE+∠COE=120°,
而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE,
在△BOD和△COE中
∴△BOD≌△COE(ASA),
∴BD=CE,OD=OE,所以①正确;
∴S△BOD=S△COE,
∴四边形ODBE的面积=S△OBC=S△ABC==,所以③正确;
作OH⊥DE,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°,
∴OH=OE,HE=OH=OE,
∴DE=OE,
∴S△ODE= OE OE=OE2,
即S△ODE随OE的变化而变化,
而四边形ODBE的面积为定值,
∴S△ODE≠S△BDE;所以②错误;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=4+OE,
当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=,
∴△BDE周长的最小值=4+2=6,所以④正确.
故答案为①③④.
15.如图,在平面直角坐标系中,点B的坐标是(﹣3,2),OA=1,将点B绕点A顺时针旋转90°得到点C,则点C的坐标是 (3,4) .
【解答】解:如图,过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,则∠ADC=∠AEB=90°,
∴∠BAE+∠ABE=90°,
根据题意得:AC=AB,∠BAC=90°,
∴∠BAE+∠CAD=90°,
∴∠ABE=∠CAD,
∴△ABE≌△CAD,
∴AD=BE,CD=AE,
∵点B的坐标是(﹣3,2),
∴OE=3,AD=BE=2,
∵OA=1,
∴OD=3,CD=AE=4,
∴点C的坐标为(3,4).
故答案为:(3,4).
16.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=6,AD=2AB,则BD的长为 10 .
【解答】解:如图,连接AC,
∵AE⊥BC,BE=CE,
∴AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG,
∴BD=CG,∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴ADG,
∵AD=2AB,∴DG=2BC,
∵BE=CE=2,
∴BC=4,∴DG=8,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADC+∠ADG=90°,∴∠GDC=90°°,
∴CG==10,
∴BD=CG=10,
故答案为:10.
17.如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= 3﹣3 .
【解答】解:在△ABC中,∵∠C=90°,∠B=30°,AB=6,
∴AC=3,BC=3,∠CAB=60°,
∵将△ABC绕点A逆时针方向旋转15°得到△AB′C′,
∴△ABC≌△AB′C′,∠C'AE=45°,
∴AC=AC'=C'E=3,BC=B'C'=3,
∴B'E=B'C'﹣C'E=3﹣3.
18.如图,在正方形ABCD中,PA=1,PB=2,PC=3,则∠APB 的度数为 135° .
【解答】解:将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP',
则△ABP'≌△CBP,AP'=CP=3,BP'=BP=2,∠PBP'=90°,
∴∠BPP'=45°,
根据勾股定理得,P'P===2,
∵AP=1,
∴AP2+P'P2=1+8=9,
又∵P'A2=32=9,
∴AP2+P'P2=P'A2,
∴△APP'是直角三角形,且∠APP'=90°,
∴∠APB=∠APP'+∠BPP'=90°+45°=135°.
故答案为:135°.
三.解答题
19.如图,△OAB中,∠AOB=60°,OA=4,点B的坐标为(6,0),将△OAB绕点A逆时针旋转得到△CAD,且点O的对应点C落在OB上.
(1)求∠OAC的度数;
(2)求点D的坐标.
【解答】解:(1)由旋转的性质可知AO=AC=4,
∵∠AOB=60°,
∴△AOC是等边三角形,
∴∠OAC=60°;
(2)如图,过点D作DE⊥x轴于点E.
∵B(6,0),
∴OB=6,
由旋转的性质可知OB=CD=6,∠ACD=∠AOB=60°,
∵△AOC是等边三角形,
∴OC=OA=4,∠ACO=60°,
∴∠DCE=60°,
∴CE=CD=3,DE=3,
∴OE=OC+CE=4+3=7,
∴D(7,3).
20.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α度的角,得到矩形CFED,设FC与AB交于点H,且A(0,4)、C(8,0).
(1)当α=60°时,△CBD的形状是 等边三角形 .
(2)当AH=HC时,求直线FC的解析式.
【解答】解:(1)∵矩形COAB绕点C顺时针旋转60度的角,得到矩形CFED,
∴∠BCD=60°,CB=CD,
∴△CBD为等边三角形;
(2)∵A(0,4)、C(8,0),
∴OA=BC=4,OC=AB=8,
设AH=HC=x,则BH=8﹣x,CB=4,
在Rt△CBH中,
∵CH2=BH2+BC2,
∴x2=(8﹣x)2+42,解得x=5,
∴H点的坐标为(5,4),
设直线FC的解析式为y=kx+b,
把C(8,0)、H(5,4)代入得,解得,
∴直线FC的解析式为.
21.如图,四边形OAFB,OCED均为正方形,OA=,OC=5.
(1)连接DB,AC,试判断AC与DB之间的数及关系和位置关系,并说明理由.
(2)在正方形OAFB绕点O旋转的过程中,(1)的结论依旧成立,当A,B,D三点共线时,求BC的长.
【解答】解:(1)DB=AC,DB⊥AC,理由如下:
如图,延长CA交BD与点G,
∵四边形OAFB,OCED均为正方形,
∴OB=OA,OD=OC,
∠AOB=∠COD=90°,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴BD=AC,∠DBO=∠CAO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,
∴∠CGB=90°,
∴DB⊥AC;
(2)①如图,连接OF交AB于点H,AC交DO于点M,
∵四边形OAFB为正方形,
∴OF⊥AB,
OH=FH=BH=AH===1,AB=2AH=2,
在Rt△DOH中,DH===7,
∴BD=DH+BH=7+1=8,
∴BD=AC=8,
∵DB⊥AC,
∴∠BAC=90°,
在Rt△ABC中,BC===;
②如图,连接OF交AB于点K,AD交OC于点N,
同理可得:DK=7,BK=1,AB=2,
∴BD=DK﹣BK=7﹣1=6,
∴AC=BD=6,
在Rt△ABC中,BC===.
综上,BC=或.
22.如图,在正方形ABCD中,P是对角线AC上的一个动点(不与点A.C重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP交BC于点E,QP延长线与边AD交于点F.
(1)连接CQ,求证:AP=CQ;
(2)若正方形的边长为4,且PC=3AP,求线段AP的长.
【解答】解:如图,过点P作PM⊥AB于M,
(1)由题意得:PB=QB,∠PBQ=∠2+∠3=90°,
∵四边形ABCD是正方形,
∴AB=CB,∠ABC=∠1+∠2=90°,
∴∠1=∠3,
在△APB和△CQB中,
∴△ABP≌△CBQ(SAS),
∴AP=CQ;
(2)由(1)知:∠ABC=90°,AB=CB;
在Rt△ABC中,∠ABC=90°,
∴AC===4,
又∵PC=3AP,
∴AC=AP+PC=AP+3AP=4AP=4
∴AP=,
故线段AP的长为.
23.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 (﹣3,1) ;
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围;
(3)在(2)条件下,当a取何值,代数式m2+2n+5取得最小值.
【解答】解:(1)由题意:Q(﹣3,1).
(2)把点Q(﹣3,1)向右平移a个单位长度,向下平移a个单位长度后,
得到的点M的坐标为(﹣3+a,1﹣a),而M在第四象限,则有,
解得a>3,
即a的范围为a>3.
(3)由(2)得,m=﹣3+a,n=1﹣a
∴m2+2n+5=(a﹣3)2+2(1﹣a)+5
=a2﹣6a+9+2﹣2a+5=a2﹣8a+16=(a﹣4)2
∵(a﹣4)2≥0,
∴当a=4时,代数式m2+2n+5的最小值为0.
24.如图1,在△ABC中,BA=BC,D、E是AC边上的两点,且满足∠DBE=∠ABC.以点B为旋转中心,将△CBE按逆时针方向旋转得到△ABF,连接DF.
(1)求证:DF=DE;
(2)如图2,若AB⊥BC,其他条件不变.求证:DE2=AD2+EC2.
【解答】(1)证明:∵∠DBE=∠ABC,
∴∠ABD+∠CBE=∠DBE=∠ABC,
∵△ABF由△CBE旋转而成,
∴BE=BF,∠ABF=∠CBE,
∴∠DBF=∠DBE,
在△DBE与△DBF中,
,
∴△DBE≌△DBF(SAS),
∴DF=DE;
(2)证明:∵将△CBE按逆时针方向旋转得到△ABF,
∴BA=BC,∠ABC=90°,
∴∠BAC=∠BCE=45°,
∴图形旋转后点C与点A重合,CE与AF重合,
∴AF=EC,
∴∠FAB=∠BCE=45°,
∴∠DAF=90°,
在Rt△ADF中,DF2=AF2+AD2,
∵AF=EC,
∴DF2=EC2+AD2,
同(1)可得DE=DF,
∴DE2=AD2+EC2.
25.如图,四边形ABCD是正方形,连接AC,将△ABC绕点A逆时针旋转α得△AEF,连接CF,O为CF的中点,连接OE,OD.
(1)如图1,当α=45°时,求证:OE=OD;
(2)如图2,当45°<α<90°时,(1)OE=OD还成立吗?请说明理由.
【解答】解:(1)由旋转的性质得:AF=AC,∠AEF=∠B=90°,AE=AB
∴∠FEC=90°
又∵O为CF的中点,
∴
同理:
∴OE=OD.
(2)当45°<α<90°时,OE=OD成立,理由如下:
连接CE,DF,如图所示:
在正方形ABCD中,AB=AD
∴AD=AE
∵O为CF的中点,
∴OC=OF
∵AF=AC
∴∠ACF=∠AFC
∵∠DAC=∠EAF
∴∠DAC﹣∠DAE=∠EAF﹣∠DAE
∴∠EAC=∠DAF
在△ACE和△AFD中,
∵AF=AC,∠EAC=∠DAF,AD=AE
∴△ACE≌△AFD(SAS)
∴CE=DF,∠ECA=∠DFA
又∵∠ACF=∠AFC
∴∠ACF﹣∠ECA=∠AFC﹣∠DFA
∴∠ECO=∠DFO
在△EOC和△DOF中,
∵EC=DF,∠ECO=∠DFO,CO=FO
∴△EOC≌△DOF(SAS)
∴EO=DO.
26.如图,将一个含45°角的三角尺的直角顶点放在点M(8,8)处,三角尺的两边分别交x轴、y轴的正半轴于A,B两点.
(1)求OA+OB的值;
(2)把三角尺绕点M旋转,在旋转的过程中保持AP平分∠OAB,AP交OM于P,PN⊥x轴于N.下列两个结论:①PN+AB的值不变;②PN+AB的值不变,其中只有一个正确,请选择正确的结论,直接写出其值.
【解答】证明:(1)作ME⊥x轴于E,MF⊥y轴于F,
∵M(8,8),
∴ME=MF=8,
∵∠AMF+∠AME=∠AMF+∠BMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
,
∴△AME≌△BMF(ASA),
∴AE=BF,
∴OA+OB=OA+OF+BF=OA+OF+AE=OE+OF=16;
(2)解:①ON+AB的值不会发生变化正确,
理由如下:过P作PQ⊥ME于Q,延长PQ到R,使QR=PQ,连接MR,
∵△AEM≌△BFM,
∴MB=MA,
∵∠AMB=90°,
∴∠MBA=∠MAB=45°,
∵OM平分∠AOB,AP平分∠BAO,∠BOA=90°,
∴∠MOA=45°,∠BAP=∠PAO,
∴∠MOA+∠PAO=∠MAB+∠BAP,
即∠MAP=∠MPA,
∴MP=MA,
∵∠MOE=45°,ME=OE=2,
∴∠OME=45°,
∵PR⊥ME,PQ=QR,
∴MP=MR,
∴MB=MP=MA=MR,
∴∠RMQ=∠PMQ=45°,
∴∠PMR=90°=∠BMA,
在△BMA和△PMR中,
,
∴△BMA≌△PMR(SAS),
∴AB=PR,
∴ON+AB=ON+PR=ON+PQ=OE=8,
即ON+AB的值不会发生变化.
27.如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM+CN=BD.
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?
若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
【解答】解:(1)结论BM+CN=BD成立,理由如下:
过点D作DE∥AC交AB于E,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥AC,
∴∠BED=∠A=60°,∠BDE=∠C=60°,
∴∠B=∠BED=∠BDE=60°,
∴△BDE是等边三角形,∠EDC=120°,
∴BD=BE=DE,∠EDN+∠CDN=120°,
∵∠EDM+∠EDN=∠MDN=120°,
∴∠CDN=∠EDM,
∵D是BC边的中点,
∴DE=BD=CD,
在△CDN和△EDM中,,
∴△CDN≌△EDM(ASA),
∴CN=EM,
∴BD=BE=BM+EM=BM+CN;
(2)上述结论不成立,BM,CN,BD之间的数量关系为:BM﹣CN=BD;理由如下:
过点D作DE∥AC交AB于E,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠NCD=120°,
∵DE∥AC,
∴∠BED=∠A=60°,∠BDE=∠ACB=60°,
∴∠B=∠BED=∠BDE=60°,
∴△BDE是等边三角形,∠MED=∠EDC=120°,
∴BD=BE=DE,∠NCD=∠MED,∠EDM+∠CDM=120°,
∵∠CDN+∠CDM=∠MDN=120°,
∴∠CDN=∠EDM,
∵D是BC边的中点,
∴DE=BD=CD,
在△CDN和△EDM中,,
∴△CDN≌△EDM(ASA),
∴CN=EM,
∴BD=BE=BM﹣EM=BM﹣CN,
∴BM﹣CN=BD.
28.如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为a.
(1)当点D′恰好落在EF边上时,求旋转角a的值;
(2)如图2,G为BC中点,且0°<a<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角a的值;若不能说明理由.
【解答】(1)解:∵长方形CEFD绕点C顺时针旋转至CE′F′D′,
∴CD′=CD=2,
在Rt△CED′中,CD′=2,CE=1,
∴∠CD′E=30°,
∵CD∥EF,
∴∠α=30°;
(2)证明:∵G为BC中点,
∴CG=1,
∴CG=CE,
∵长方形CEFD绕点C顺时针旋转至CE′F′D′,
∴∠D′CE′=∠DCE=90°,CE=CE′=CG,
∴∠GCD′=∠DCE′=90°+α,
在△GCD′和△E′CD中
,
∴△GCD′≌△E′CD(SAS),
∴GD′=E′D;
(3)解:能.理由如下:
∵四边形ABCD为正方形,
∴CB=CD,
∵CD=CD′,
∴△BCD′与△DCD′为腰相等的两等腰三角形,
当∠BCD′=∠DCD′时,△BCD′≌△DCD′,
当△BCD′与△DCD′为钝角三角形时,则旋转角α==135°,
当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′=∠BCD=45°
则α=360°﹣=315°,
即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.
一.选择题
1.下列图形分别绕某个点旋转120°后不能与自身重合的是( )
A. B. C. D.
2.在平面直角坐标系中,将点P(4,3)绕原点旋转180°后,得到对应点Q的坐标是( )
A.(4,﹣3) B.(﹣4,3) C.(3,4) D.(﹣4,﹣3)
3.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB=CB′,则∠C′的度数为( )
A.18° B.20° C.24° D.28°
4.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
5.如图,将平行四边形ABCD绕点A逆时针旋转到平行四边形A′B′C′D′的位置,使点B'落在BC上,B′C′与CD交于点E,若AB=3,BC=4,BB′=1,则CE的长为( )
A. B. C. D.1
6.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.则下列结论不正确的是( )
A.∠EAF=45° B.△EBF为等腰直角三角形
C.AE平分∠DAF D.BE+CD>ED
第3题图 第4题图 第5题图 第6题图
7.如图,在4×4的正方形网格中,△MPN绕某点旋转一定的角度,得到△M'P'N',其旋转中心是( )
A.点A B.点B C.点C D.点D
8.如图,在等边三角形ABC中,点P是△ABC内一点,PA=3,PB=5,PC=4,则∠CPA的度数为( )
A.160° B.155° C.150° D.145°
9.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2023次得到正方OA2023B2023C2023,如果点A的坐标为(1,0),那么B2023的坐标为( )
A.(1,1) B. C. D.(﹣1,﹣1)
10.如图,O是等边△ABC内一点,OA=3,OC=5,OB=4,将线段BO以点B为旋转中心,逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④;
其中结论正确有( )个.
A.4 B.3 C.2 D.1
11.如图,C为线段BE上一动点(不与点B,E重合),在BE同侧分别作等边△ABC和等边△CDE、BD与AE交于点P,BD与AC交于点M,AE与CD交于点N,连结MN.以下四个结论:①CM=CN;②∠APB=60°;③PA+PC=PB;④PC平分∠BPE,恒成立的结论有( )
A.①②④ B.①②③④ C.①③④ D.①④
12.如图,已知△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转n°(0<n<∠BAC)得到△ADE,AD交于点F,DE交BC,AC于点G,H,则以下结论:
①△ABF≌△AEH;
②连接AG,FH,则AG⊥FH;
③当AD⊥BC时,DF的长度最大;
④当H点是DE的中点时,四边形AFGH的面积等于AF×GH.
其中正确的个数有( )
A.4个 B.3个 C.5个 D.1个
二.填空题
13.如图,在等腰△ABC中,AB=AC,∠C=25°,将△ABC绕点B逆时针旋转至△DBE且点A的对应点D落在CA延长线上,则∠CBE= .
14.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:
①OD=OE;
②S△ODE=S△BDE;
③四边形ODBE的面积始终等于;
④△BDE周长的最小值为6.
上述结论中正确的有 (写出序号).
15.如图,在平面直角坐标系中,点B的坐标是(﹣3,2),OA=1,将点B绕点A顺时针旋转90°得到点C,则点C的坐标是 .
16.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=6,AD=2AB,则BD的长为 .
17.如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
18.如图,在正方形ABCD中,PA=1,PB=2,PC=3,则∠APB 的度数为 .
三.解答题
19.如图,△OAB中,∠AOB=60°,OA=4,点B的坐标为(6,0),将△OAB绕点A逆时针旋转得到△CAD,且点O的对应点C落在OB上.
(1)求∠OAC的度数;
(2)求点D的坐标.
20.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α度的角,得到矩形CFED,设FC与AB交于点H,且A(0,4)、C(8,0).
(1)当α=60°时,△CBD的形状是 .
(2)当AH=HC时,求直线FC的解析式.
21.如图,四边形OAFB,OCED均为正方形,OA=,OC=5.
(1)连接DB,AC,试判断AC与DB之间的数及关系和位置关系,并说明理由.
(2)在正方形OAFB绕点O旋转的过程中,(1)的结论依旧成立,当A,B,D三点共线时,求BC的长.
22.如图,在正方形ABCD中,P是对角线AC上的一个动点(不与点A.C重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP交BC于点E,QP延长线与边AD交于点F.
(1)连接CQ,求证:AP=CQ;
(2)若正方形的边长为4,且PC=3AP,求线段AP的长.
23.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 ;
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围;
(3)在(2)条件下,当a取何值,代数式m2+2n+5取得最小值.
24.如图1,在△ABC中,BA=BC,D、E是AC边上的两点,且满足∠DBE=∠ABC.以点B为旋转中心,将△CBE按逆时针方向旋转得到△ABF,连接DF.
(1)求证:DF=DE;
(2)如图2,若AB⊥BC,其他条件不变.求证:DE2=AD2+EC2.
25.如图,四边形ABCD是正方形,连接AC,将△ABC绕点A逆时针旋转α得△AEF,连接CF,O为CF的中点,连接OE,OD.
(1)如图1,当α=45°时,求证:OE=OD;
(2)如图2,当45°<α<90°时,(1)OE=OD还成立吗?请说明理由.
26.如图,将一个含45°角的三角尺的直角顶点放在点M(8,8)处,三角尺的两边分别交x轴、y轴的正半轴于A,B两点.
(1)求OA+OB的值;
(2)把三角尺绕点M旋转,在旋转的过程中保持AP平分∠OAB,AP交OM于P,PN⊥x轴于N.下列两个结论:①PN+AB的值不变;②PN+AB的值不变,其中只有一个正确,请选择正确的结论,直接写出其值.
27.如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM+CN=BD.
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?
若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
28.如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为a.
(1)当点D′恰好落在EF边上时,求旋转角a的值;
(2)如图2,G为BC中点,且0°<a<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角a的值;若不能说明理由.
23.1 图形的旋转(提升练习)
一.选择题
1.下列图形分别绕某个点旋转120°后不能与自身重合的是( )
A. B. C. D.
【解答】解:A、等边三角形绕它的中心旋转120°能与本身重合,本选项不符合题意.
B、圆绕圆心旋转任意角度能与本身重合,本选项不符合题意.
C、这个图形绕中心性质120°能与本身重合,本选项不符合题意.
D、五角星绕中心旋转72°与本身重合,本选项符合题意.
故选:D.
2.在平面直角坐标系中,将点P(4,3)绕原点旋转180°后,得到对应点Q的坐标是( )
A.(4,﹣3) B.(﹣4,3) C.(3,4) D.(﹣4,﹣3)
【解答】解:∵将点P(4,3)绕原点O旋转180°后,得到的对应点Q,
∴点Q和点P关于原点对称,
∵点P的坐标为(4,3),
∴点Q的坐标是(﹣4,﹣3).
故选:D.
3.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB=CB′,则∠C′的度数为( )
A.18° B.20° C.24° D.28°
【解答】解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣108°,
∴∠C=24°,
∴∠C'=∠C=24°,
故选:C.
4.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
【解答】解:如图,过点A作AE⊥OB于E,过点A′作A′H⊥x轴于H.
∵B(2,0),△AOB是等边三角形,
∴OA=OB=AB=2,
∵AE⊥OB,
∴OE=EB=1,
∴AE===,
∵A′H⊥OH,
∴∠A′HO=∠AEO=∠AOA′=90°,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(﹣,1),
故选:C.
5.如图,将平行四边形ABCD绕点A逆时针旋转到平行四边形A′B′C′D′的位置,使点B'落在BC上,B′C′与CD交于点E,若AB=3,BC=4,BB′=1,则CE的长为( )
A. B. C. D.1
【解答】解:如图,连接DD',
由旋转可知,∠BAB′=∠DAD′,AB′=AB=3,AD′=AD=4,
∴△BAB′∽△DAD′,
∴AB:BB′=AD:DD′=3:1,∠AD′D=∠AB′B=∠B,
∴DD′=,
又∵∠AD′C′=∠AB′C′=∠B,∠AD′D=∠B=∠AB′B,
∴∠AD′C′=∠AD′D,即点D′,D,C′在同一条直线上,
∴DC′=,
又∠C′=∠ECB′,∠DEC′=∠B′EC,
∴△CEB′∽△C'ED,
∴B′E:DE=CE:C′E=B′C:DC′,即B′E:DE=CE:C′E=3:,
设CE=x,B'E=y,
∴x:(4﹣y)=y:(3﹣x)=3:,
∴x=,
∴CE=,
故选:A.
6.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.则下列结论不正确的是( )
A.∠EAF=45° B.△EBF为等腰直角三角形
C.AE平分∠DAF D.BE+CD>ED
【解答】解:∵△ADC绕点A顺时针旋转90°后,得到△AFB,
∴△ADC≌△AFB,∠FAD=90°,AD=AF,BF=CD,
∵∠DAE=45°,
∴∠EAF=90°﹣∠DAE=45°,所以A正确,不符合题意;
∴∠DAE=∠EAF,
∴AE平分∠DAF,所以C正确,不符合题意;
,
∴△AED≌△AEF(SAS),
∴ED=EF,
∵BE+BF>EF,
∴BE+CD>ED,
所以D正确,不符合题意;
在Rt△ABC中,AB=AC,
∴∠ABC=∠ACB=45°,
∵△ADC≌△AFB,
∴∠ACD=∠ABF=45°,
∵∠ABF+∠ABE=∠ACD+∠ABC=90°,
∴△EBF为直角三角形,
但是BE、CD不一定相等,所以BE、BF不一定相等,所以B不正确,符合题意.
故选:B.
7.如图,在4×4的正方形网格中,△MPN绕某点旋转一定的角度,得到△M'P'N',其旋转中心是( )
A.点A B.点B C.点C D.点D
【解答】解:如图,由旋转可知:P和P'为对应点,N和N'为对应点,
连接PP'、NN',作PP'、NN'的垂直平分线,
可得:点B为旋转中心,
故选:B.
8.如图,在等边三角形ABC中,点P是△ABC内一点,PA=3,PB=5,PC=4,则∠CPA的度数为( )
A.160° B.155° C.150° D.145°
【解答】解:如图,将△ACP绕点A顺时针旋转60°,得到△ABE,连接PE,
∴△ACP≌△ABE,∠PAE=60°,
∴AP=AE=3,CP=BE=4,∠AEB=∠APC,
∴△PAE是等边三角形,
∴PE=AE=3,∠AEP=60°,
∵PB2=25,PE2+BE2=9+16=25,
∴PB2=PE2+BE2,
∴∠PEB=90°,
∴∠AEB=150°=∠APC,
故选:C.
9.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2023次得到正方OA2023B2023C2023,如果点A的坐标为(1,0),那么B2023的坐标为( )
A.(1,1) B. C. D.(﹣1,﹣1)
【解答】解:∵点A的坐标为(1,0),
∴OA=1,
∵四边形OABC是正方形,
∴∠OAB=90°,AB=OA=1,
∴B(2,2),
连接OB,如图:
由勾股定理得:,
由旋转的性质得:,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴,B2(﹣1,1),,B4(﹣1,﹣1),,B6(1,﹣1),,…,
发现是8次一循环,则2023÷8=252…7,
∴点B2023的坐标为,
故选:B.
10.如图,O是等边△ABC内一点,OA=3,OC=5,OB=4,将线段BO以点B为旋转中心,逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④;
其中结论正确有( )个.
A.4 B.3 C.2 D.1
【解答】解:连接OO′,
∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC,
∵将线段BO以点B为旋转中心,逆时针旋转60°得到线段BO′,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到;
故①是正确的;
∵OB=OB,∠OBO′=60°,
∴△O′BO是等边三角形,
∴OO′=OB=4,
故②是正确的;
∵△O′BO是等边三角形,
∴∠O′OB=60°,
∵OO′=OB=4,AO=3,AO′=OC=5,
∴∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=150°,
故③是正确的;
④S四边形AOBO′=S△AOO′+S△OO′B=(4×4×+4×3)=4+6,
故③是错误的,
故选:B.
11.如图,C为线段BE上一动点(不与点B,E重合),在BE同侧分别作等边△ABC和等边△CDE、BD与AE交于点P,BD与AC交于点M,AE与CD交于点N,连结MN.以下四个结论:①CM=CN;②∠APB=60°;③PA+PC=PB;④PC平分∠BPE,恒成立的结论有( )
A.①②④ B.①②③④ C.①③④ D.①④
【解答】解:∵△ABC和△DCE都为等边三角形,
∴CA=CB,∠ACB=60°,CD=CE,∠DCE=60°,
∴∠BCD=∠ACE=120°,
在△BCD和△ACE中,
,
∴△BCD≌△ACE(SAS),
∴∠CBD=∠CAE,
∵∠AMP=∠CMB,
∴∠APM=∠BCM=60°,
即∠APB=60°,所以②正确;
∵∠ACB=∠DCE=60°,
∴∠ACN=60°,
在△BCM和△ACN中,
,
∴△BCM≌△ACN(ASA),
∴CM=CN,所以①正确;
过C点作CH⊥BD于H点,CQ⊥AE于Q点,如图,
∵△BCD≌△ACE,
∴CH=CQ,
∴PC平分∠BPE,所以④正确;
∵∠APB=60°,
∴∠BPE=120°,
∴∠BPC=60°,
在PB上截取PG=PC,如图,则△PCG为等边三角形,
∴CG=PG=PC,∠PGC=60°,
∵∠APC=∠APB+∠BPC=120°,∠BGC=180°﹣∠PGC=120°,
∴∠APC=∠BGC,
在△BCG和△ACP中,
,
∴△BCG≌△ACP(AAS),
∴BG=AP,
∴PA+PC=BG+PG=PB,所以③正确.
故选:B.
12.如图,已知△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转n°(0<n<∠BAC)得到△ADE,AD交于点F,DE交BC,AC于点G,H,则以下结论:
①△ABF≌△AEH;
②连接AG,FH,则AG⊥FH;
③当AD⊥BC时,DF的长度最大;
④当H点是DE的中点时,四边形AFGH的面积等于AF×GH.
其中正确的个数有( )
A.4个 B.3个 C.5个 D.1个
【解答】解:①∵AB=AC,
∴∠B=∠C,
由旋转得AB=AC=AE,∠BAF=∠HAE,∠B=∠C=∠E,
∴△ABF≌△AEH(ASA),故①正确;
②连接AG、FH,
∵△ABF≌△AEH,
∴∠AFB=∠AHE,AF=AH,
∵∠AFB=∠DFG,∠AHE=∠CHG,
∴∠DFG=∠CHG,
∵AD=AB=AC,∴DF=CH,
又∵∠DGF=∠CGH,
∴△DFG≌△CHG(AAS),
∴FG=GH,
∴AG垂直平分FH,故②正确;
③∵DF=AD﹣AF,AD是定长,
∴AF最小时,DF最长,
∴AD⊥BC时,DF的长度最大,故③正确;
④∵AD=AE,
∴当点H是DE的中点时,有AH⊥DE,
∵AF=AH,FG=GH,AG=AG,
∴△AFG≌△AHG(SSS),
∴S四边形AFGH=2S△AGH=2×GH×AH=GH×AF,故④正确.
故选:A.
二.填空题
13.如图,在等腰△ABC中,AB=AC,∠C=25°,将△ABC绕点B逆时针旋转至△DBE且点A的对应点D落在CA延长线上,则∠CBE= 80° .
【解答】解:∵AB=AC,
∴∠C=∠ABC=25°,
∴∠BAD=50°,
∵将△ABC绕点B逆时针旋转至△DBE,
∴AB=BD,∠ABC=∠DBE=25°,∠CBE=∠DBE,
∴∠BDA=∠BAD=50°,
∴∠DBA=80°,
∴∠CBE=∠DBE=80°,
故答案为:80°.
14.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:
①OD=OE;
②S△ODE=S△BDE;
③四边形ODBE的面积始终等于;
④△BDE周长的最小值为6.
上述结论中正确的有 ①③④ (写出序号).
【解答】解:连接OB、OC,如图,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O是△ABC的中心,
∴OB=OC,OB、OC分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=∠OCB=30°,
∴∠BOC=120°,即∠BOE+∠COE=120°,
而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE,
在△BOD和△COE中
∴△BOD≌△COE(ASA),
∴BD=CE,OD=OE,所以①正确;
∴S△BOD=S△COE,
∴四边形ODBE的面积=S△OBC=S△ABC==,所以③正确;
作OH⊥DE,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°,
∴OH=OE,HE=OH=OE,
∴DE=OE,
∴S△ODE= OE OE=OE2,
即S△ODE随OE的变化而变化,
而四边形ODBE的面积为定值,
∴S△ODE≠S△BDE;所以②错误;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=4+OE,
当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=,
∴△BDE周长的最小值=4+2=6,所以④正确.
故答案为①③④.
15.如图,在平面直角坐标系中,点B的坐标是(﹣3,2),OA=1,将点B绕点A顺时针旋转90°得到点C,则点C的坐标是 (3,4) .
【解答】解:如图,过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,则∠ADC=∠AEB=90°,
∴∠BAE+∠ABE=90°,
根据题意得:AC=AB,∠BAC=90°,
∴∠BAE+∠CAD=90°,
∴∠ABE=∠CAD,
∴△ABE≌△CAD,
∴AD=BE,CD=AE,
∵点B的坐标是(﹣3,2),
∴OE=3,AD=BE=2,
∵OA=1,
∴OD=3,CD=AE=4,
∴点C的坐标为(3,4).
故答案为:(3,4).
16.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=6,AD=2AB,则BD的长为 10 .
【解答】解:如图,连接AC,
∵AE⊥BC,BE=CE,
∴AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG,
∴BD=CG,∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴ADG,
∵AD=2AB,∴DG=2BC,
∵BE=CE=2,
∴BC=4,∴DG=8,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADC+∠ADG=90°,∴∠GDC=90°°,
∴CG==10,
∴BD=CG=10,
故答案为:10.
17.如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= 3﹣3 .
【解答】解:在△ABC中,∵∠C=90°,∠B=30°,AB=6,
∴AC=3,BC=3,∠CAB=60°,
∵将△ABC绕点A逆时针方向旋转15°得到△AB′C′,
∴△ABC≌△AB′C′,∠C'AE=45°,
∴AC=AC'=C'E=3,BC=B'C'=3,
∴B'E=B'C'﹣C'E=3﹣3.
18.如图,在正方形ABCD中,PA=1,PB=2,PC=3,则∠APB 的度数为 135° .
【解答】解:将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP',
则△ABP'≌△CBP,AP'=CP=3,BP'=BP=2,∠PBP'=90°,
∴∠BPP'=45°,
根据勾股定理得,P'P===2,
∵AP=1,
∴AP2+P'P2=1+8=9,
又∵P'A2=32=9,
∴AP2+P'P2=P'A2,
∴△APP'是直角三角形,且∠APP'=90°,
∴∠APB=∠APP'+∠BPP'=90°+45°=135°.
故答案为:135°.
三.解答题
19.如图,△OAB中,∠AOB=60°,OA=4,点B的坐标为(6,0),将△OAB绕点A逆时针旋转得到△CAD,且点O的对应点C落在OB上.
(1)求∠OAC的度数;
(2)求点D的坐标.
【解答】解:(1)由旋转的性质可知AO=AC=4,
∵∠AOB=60°,
∴△AOC是等边三角形,
∴∠OAC=60°;
(2)如图,过点D作DE⊥x轴于点E.
∵B(6,0),
∴OB=6,
由旋转的性质可知OB=CD=6,∠ACD=∠AOB=60°,
∵△AOC是等边三角形,
∴OC=OA=4,∠ACO=60°,
∴∠DCE=60°,
∴CE=CD=3,DE=3,
∴OE=OC+CE=4+3=7,
∴D(7,3).
20.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α度的角,得到矩形CFED,设FC与AB交于点H,且A(0,4)、C(8,0).
(1)当α=60°时,△CBD的形状是 等边三角形 .
(2)当AH=HC时,求直线FC的解析式.
【解答】解:(1)∵矩形COAB绕点C顺时针旋转60度的角,得到矩形CFED,
∴∠BCD=60°,CB=CD,
∴△CBD为等边三角形;
(2)∵A(0,4)、C(8,0),
∴OA=BC=4,OC=AB=8,
设AH=HC=x,则BH=8﹣x,CB=4,
在Rt△CBH中,
∵CH2=BH2+BC2,
∴x2=(8﹣x)2+42,解得x=5,
∴H点的坐标为(5,4),
设直线FC的解析式为y=kx+b,
把C(8,0)、H(5,4)代入得,解得,
∴直线FC的解析式为.
21.如图,四边形OAFB,OCED均为正方形,OA=,OC=5.
(1)连接DB,AC,试判断AC与DB之间的数及关系和位置关系,并说明理由.
(2)在正方形OAFB绕点O旋转的过程中,(1)的结论依旧成立,当A,B,D三点共线时,求BC的长.
【解答】解:(1)DB=AC,DB⊥AC,理由如下:
如图,延长CA交BD与点G,
∵四边形OAFB,OCED均为正方形,
∴OB=OA,OD=OC,
∠AOB=∠COD=90°,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴BD=AC,∠DBO=∠CAO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,
∴∠CGB=90°,
∴DB⊥AC;
(2)①如图,连接OF交AB于点H,AC交DO于点M,
∵四边形OAFB为正方形,
∴OF⊥AB,
OH=FH=BH=AH===1,AB=2AH=2,
在Rt△DOH中,DH===7,
∴BD=DH+BH=7+1=8,
∴BD=AC=8,
∵DB⊥AC,
∴∠BAC=90°,
在Rt△ABC中,BC===;
②如图,连接OF交AB于点K,AD交OC于点N,
同理可得:DK=7,BK=1,AB=2,
∴BD=DK﹣BK=7﹣1=6,
∴AC=BD=6,
在Rt△ABC中,BC===.
综上,BC=或.
22.如图,在正方形ABCD中,P是对角线AC上的一个动点(不与点A.C重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP交BC于点E,QP延长线与边AD交于点F.
(1)连接CQ,求证:AP=CQ;
(2)若正方形的边长为4,且PC=3AP,求线段AP的长.
【解答】解:如图,过点P作PM⊥AB于M,
(1)由题意得:PB=QB,∠PBQ=∠2+∠3=90°,
∵四边形ABCD是正方形,
∴AB=CB,∠ABC=∠1+∠2=90°,
∴∠1=∠3,
在△APB和△CQB中,
∴△ABP≌△CBQ(SAS),
∴AP=CQ;
(2)由(1)知:∠ABC=90°,AB=CB;
在Rt△ABC中,∠ABC=90°,
∴AC===4,
又∵PC=3AP,
∴AC=AP+PC=AP+3AP=4AP=4
∴AP=,
故线段AP的长为.
23.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 (﹣3,1) ;
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围;
(3)在(2)条件下,当a取何值,代数式m2+2n+5取得最小值.
【解答】解:(1)由题意:Q(﹣3,1).
(2)把点Q(﹣3,1)向右平移a个单位长度,向下平移a个单位长度后,
得到的点M的坐标为(﹣3+a,1﹣a),而M在第四象限,则有,
解得a>3,
即a的范围为a>3.
(3)由(2)得,m=﹣3+a,n=1﹣a
∴m2+2n+5=(a﹣3)2+2(1﹣a)+5
=a2﹣6a+9+2﹣2a+5=a2﹣8a+16=(a﹣4)2
∵(a﹣4)2≥0,
∴当a=4时,代数式m2+2n+5的最小值为0.
24.如图1,在△ABC中,BA=BC,D、E是AC边上的两点,且满足∠DBE=∠ABC.以点B为旋转中心,将△CBE按逆时针方向旋转得到△ABF,连接DF.
(1)求证:DF=DE;
(2)如图2,若AB⊥BC,其他条件不变.求证:DE2=AD2+EC2.
【解答】(1)证明:∵∠DBE=∠ABC,
∴∠ABD+∠CBE=∠DBE=∠ABC,
∵△ABF由△CBE旋转而成,
∴BE=BF,∠ABF=∠CBE,
∴∠DBF=∠DBE,
在△DBE与△DBF中,
,
∴△DBE≌△DBF(SAS),
∴DF=DE;
(2)证明:∵将△CBE按逆时针方向旋转得到△ABF,
∴BA=BC,∠ABC=90°,
∴∠BAC=∠BCE=45°,
∴图形旋转后点C与点A重合,CE与AF重合,
∴AF=EC,
∴∠FAB=∠BCE=45°,
∴∠DAF=90°,
在Rt△ADF中,DF2=AF2+AD2,
∵AF=EC,
∴DF2=EC2+AD2,
同(1)可得DE=DF,
∴DE2=AD2+EC2.
25.如图,四边形ABCD是正方形,连接AC,将△ABC绕点A逆时针旋转α得△AEF,连接CF,O为CF的中点,连接OE,OD.
(1)如图1,当α=45°时,求证:OE=OD;
(2)如图2,当45°<α<90°时,(1)OE=OD还成立吗?请说明理由.
【解答】解:(1)由旋转的性质得:AF=AC,∠AEF=∠B=90°,AE=AB
∴∠FEC=90°
又∵O为CF的中点,
∴
同理:
∴OE=OD.
(2)当45°<α<90°时,OE=OD成立,理由如下:
连接CE,DF,如图所示:
在正方形ABCD中,AB=AD
∴AD=AE
∵O为CF的中点,
∴OC=OF
∵AF=AC
∴∠ACF=∠AFC
∵∠DAC=∠EAF
∴∠DAC﹣∠DAE=∠EAF﹣∠DAE
∴∠EAC=∠DAF
在△ACE和△AFD中,
∵AF=AC,∠EAC=∠DAF,AD=AE
∴△ACE≌△AFD(SAS)
∴CE=DF,∠ECA=∠DFA
又∵∠ACF=∠AFC
∴∠ACF﹣∠ECA=∠AFC﹣∠DFA
∴∠ECO=∠DFO
在△EOC和△DOF中,
∵EC=DF,∠ECO=∠DFO,CO=FO
∴△EOC≌△DOF(SAS)
∴EO=DO.
26.如图,将一个含45°角的三角尺的直角顶点放在点M(8,8)处,三角尺的两边分别交x轴、y轴的正半轴于A,B两点.
(1)求OA+OB的值;
(2)把三角尺绕点M旋转,在旋转的过程中保持AP平分∠OAB,AP交OM于P,PN⊥x轴于N.下列两个结论:①PN+AB的值不变;②PN+AB的值不变,其中只有一个正确,请选择正确的结论,直接写出其值.
【解答】证明:(1)作ME⊥x轴于E,MF⊥y轴于F,
∵M(8,8),
∴ME=MF=8,
∵∠AMF+∠AME=∠AMF+∠BMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
,
∴△AME≌△BMF(ASA),
∴AE=BF,
∴OA+OB=OA+OF+BF=OA+OF+AE=OE+OF=16;
(2)解:①ON+AB的值不会发生变化正确,
理由如下:过P作PQ⊥ME于Q,延长PQ到R,使QR=PQ,连接MR,
∵△AEM≌△BFM,
∴MB=MA,
∵∠AMB=90°,
∴∠MBA=∠MAB=45°,
∵OM平分∠AOB,AP平分∠BAO,∠BOA=90°,
∴∠MOA=45°,∠BAP=∠PAO,
∴∠MOA+∠PAO=∠MAB+∠BAP,
即∠MAP=∠MPA,
∴MP=MA,
∵∠MOE=45°,ME=OE=2,
∴∠OME=45°,
∵PR⊥ME,PQ=QR,
∴MP=MR,
∴MB=MP=MA=MR,
∴∠RMQ=∠PMQ=45°,
∴∠PMR=90°=∠BMA,
在△BMA和△PMR中,
,
∴△BMA≌△PMR(SAS),
∴AB=PR,
∴ON+AB=ON+PR=ON+PQ=OE=8,
即ON+AB的值不会发生变化.
27.如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM+CN=BD.
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?
若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
【解答】解:(1)结论BM+CN=BD成立,理由如下:
过点D作DE∥AC交AB于E,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥AC,
∴∠BED=∠A=60°,∠BDE=∠C=60°,
∴∠B=∠BED=∠BDE=60°,
∴△BDE是等边三角形,∠EDC=120°,
∴BD=BE=DE,∠EDN+∠CDN=120°,
∵∠EDM+∠EDN=∠MDN=120°,
∴∠CDN=∠EDM,
∵D是BC边的中点,
∴DE=BD=CD,
在△CDN和△EDM中,,
∴△CDN≌△EDM(ASA),
∴CN=EM,
∴BD=BE=BM+EM=BM+CN;
(2)上述结论不成立,BM,CN,BD之间的数量关系为:BM﹣CN=BD;理由如下:
过点D作DE∥AC交AB于E,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠NCD=120°,
∵DE∥AC,
∴∠BED=∠A=60°,∠BDE=∠ACB=60°,
∴∠B=∠BED=∠BDE=60°,
∴△BDE是等边三角形,∠MED=∠EDC=120°,
∴BD=BE=DE,∠NCD=∠MED,∠EDM+∠CDM=120°,
∵∠CDN+∠CDM=∠MDN=120°,
∴∠CDN=∠EDM,
∵D是BC边的中点,
∴DE=BD=CD,
在△CDN和△EDM中,,
∴△CDN≌△EDM(ASA),
∴CN=EM,
∴BD=BE=BM﹣EM=BM﹣CN,
∴BM﹣CN=BD.
28.如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为a.
(1)当点D′恰好落在EF边上时,求旋转角a的值;
(2)如图2,G为BC中点,且0°<a<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角a的值;若不能说明理由.
【解答】(1)解:∵长方形CEFD绕点C顺时针旋转至CE′F′D′,
∴CD′=CD=2,
在Rt△CED′中,CD′=2,CE=1,
∴∠CD′E=30°,
∵CD∥EF,
∴∠α=30°;
(2)证明:∵G为BC中点,
∴CG=1,
∴CG=CE,
∵长方形CEFD绕点C顺时针旋转至CE′F′D′,
∴∠D′CE′=∠DCE=90°,CE=CE′=CG,
∴∠GCD′=∠DCE′=90°+α,
在△GCD′和△E′CD中
,
∴△GCD′≌△E′CD(SAS),
∴GD′=E′D;
(3)解:能.理由如下:
∵四边形ABCD为正方形,
∴CB=CD,
∵CD=CD′,
∴△BCD′与△DCD′为腰相等的两等腰三角形,
当∠BCD′=∠DCD′时,△BCD′≌△DCD′,
当△BCD′与△DCD′为钝角三角形时,则旋转角α==135°,
当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′=∠BCD=45°
则α=360°﹣=315°,
即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.
同课章节目录
