12.3 角的平分线的性质 提升练习 (含解析)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 12.3 角的平分线的性质 提升练习 (含解析)2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 502.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 23:49:58 | ||
图片预览



文档简介
12.3 角的平分线的性质(提升练习)
一.选择题
1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,CD=3,则△ABD的面积为( )
A.60 B.30 C.15 D.10
2.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P且与AB垂直.若AD=8,BC=10,则△BCP的面积为( )
A.16 B.20 C.40 D.80
3.如图,AD是△ABC中∠BAC的平分线,DE⊥AB,交AB于点E,DF⊥AC,交AC于点F.若S△ABC=7,DE=2,AB=4,则AC的长是( )
A.4 B.3 C.6 D.5
4.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.12 C.8 D.6
5.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是∠ABC的平分线,BE交AD于点F,下面说法:①∠BAD=∠C;②AE=AF;③∠CAD=2∠CBE;④S△BCE=BC AE.其中正确的说法有( )个.
A.1 B.2 C.3 D.4
6.如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO的面积为30,则△ACO的面积为( )
A.18 B.20 C.22 D.24
7.在Rt△ABC中,∠C=90°,小丽进行如图步骤尺规作图,根据操作,对下列判断正确的序号是( )
①AD平分∠BAC
②AD是△ABC的中线
③S△ADC=S△ABD④S△ADC=2S△ADG
A.①②③④ B.③④ C.②③ D.②③④
8.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
9.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为从N.现有四个结论:
①CP平分∠ACF;
②∠BPC=∠BAC;
③∠APC=90°﹣∠ABC;
④S△APM+S△CPN>S△APC.
其中结论正确的是( )(填写结论的编号)
A.①②③ B.①②③④ C.②③④ D.①③④
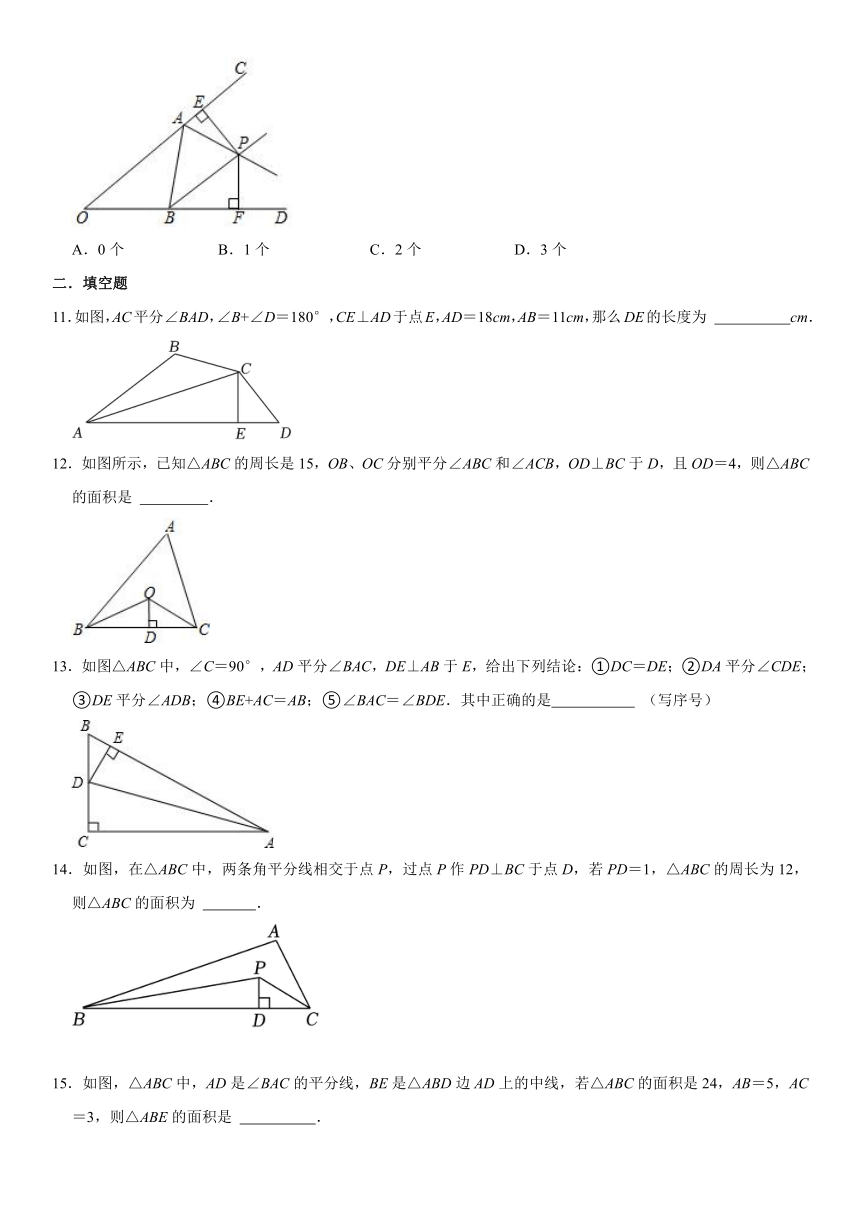
10.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
11.如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD于点E,AD=18cm,AB=11cm,那么DE的长度为 cm.
12.如图所示,已知△ABC的周长是15,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 .
13.如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是 (写序号)
14.如图,在△ABC中,两条角平分线相交于点P,过点P作PD⊥BC于点D,若PD=1,△ABC的周长为12,则△ABC的面积为 .
15.如图,△ABC中,AD是∠BAC的平分线,BE是△ABD边AD上的中线,若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是 .
16.如图,在四边形ABCD中,∠A=90°,AD=10,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP的最小值为 .
三.解答题
17.如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)若AB=20,AC=16,DE=6,求S△ABC.
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
19.如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
20.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
21.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
22.如图,△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,EF⊥BC,FM⊥AC,垂足分别是D,F,M,求证:FM=FD.
23.如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.
(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:AO平分∠BAC.
(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
24.如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
25.已知直线EF与直线AB、CD分别交于E、F两点,∠BEF和∠DFE的角平分线交于点P,且∠BEP+∠DFP=90°.
(1)求证:AB∥CD;
(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;
(3)如图3,若∠BEP=60°,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时开始旋转,当射线EP1∥FP2时,求满足条件的t的值为多少.
12.3 角的平分线的性质(提升练习)
一.选择题
1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,CD=3,则△ABD的面积为( )
A.60 B.30 C.15 D.10
【解答】解:过点D作DE⊥AB,垂足为E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC=3,
∵AB=10,
∴△ABD的面积=AB DE=×10×3=15,
故选:C.
2.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P且与AB垂直.若AD=8,BC=10,则△BCP的面积为( )
A.16 B.20 C.40 D.80
【解答】解:过P作PE⊥BC于E,
∵AB∥CD,
∴∠BAP+∠CDP=180°,
∵AD⊥AB,
∴∠BAP=90°,∴∠CDP=90°,
即AD⊥CD,
∵PE⊥BC,BP和CP分别平分∠ABC和∠BCD,
∴PA=PE,PE=PD,
∴PA=PD,
∵AD=8,
∴PE=PD=AP=4,
∵BC=10,
∴△BCP的面积为==20.
故选:B.
3.如图,AD是△ABC中∠BAC的平分线,DE⊥AB,交AB于点E,DF⊥AC,交AC于点F.若S△ABC=7,DE=2,AB=4,则AC的长是( )
A.4 B.3 C.6 D.5
【解答】解:∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴7=×4×2+×AC×2,
解得AC=3.
故选:B.
4.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.12 C.8 D.6
【解答】解:过点D作DE⊥BC,交BC于点E,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴DA=DE=3,
∴.
故选:A.
5.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是∠ABC的平分线,BE交AD于点F,下面说法:①∠BAD=∠C;②AE=AF;③∠CAD=2∠CBE;④S△BCE=BC AE.其中正确的说法有( )个.
A.1 B.2 C.3 D.4
【解答】解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠BAC=90°,AD是BC边上的高,
∴∠ABC+∠C=90°,∠CAD+∠C=90°,∠ABD+∠BAD=90°
∴∠ABC=∠CAD,∠C=∠BAD,
∴∠CAD=2∠CBE.
故①③符合题意.
∵∠BAC=90°,AD是BC边上的高,
∴∠ABE+∠AEB=90°,∠CBE+∠BFD=90°,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠BFD=∠AFE,
∴∠AEB=∠AFE,
∴AE=AF.
故②符合题意.
如图,过点E作EP⊥BC于P,
∵∠BAC=90°,BE是∠ABC的平分线,
∴AE=EP,
S△BCE=BC EP=BC AE,
故④符合题意.
故选:D.
6.如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO的面积为30,则△ACO的面积为( )
A.18 B.20 C.22 D.24
【解答】解:∵点O是三条角平分线的交点,
∴点O到AB,AC的距离相等,
∴△AOB、△AOC面积的比=AB:AC=10:8=5:4.
∵△ABO的面积为30,
∴△ACO的面积为24.
故选:D.
7.在Rt△ABC中,∠C=90°,小丽进行如图步骤尺规作图,根据操作,对下列判断正确的序号是( )
①AD平分∠BAC
②AD是△ABC的中线
③S△ADC=S△ABD④S△ADC=2S△ADG
A.①②③④ B.③④ C.②③ D.②③④
【解答】解:由作法得DG垂直平分BC,
∴DG⊥BC,BD=CD,
∴AD为△ABC的中线,所以①错误;
∵EF是线段BC的垂直平分线,
∴D是线段BC的中点,
∴AD是△ABC的中线,所以②正确;
∵∠C=90°,
∴DG∥AC,
∴DG为△ABC的中位线,
∴AC=2DG,
BG=AG,
∴S△ADC=S△ABD,所以③正确;
S△ADG=S△BDG,
∴S△ADC=2S△ADG,所以④正确.
故选:D.
8.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
【解答】解:∵OP平分∠AOB,PA⊥OA,PB⊥OB,
∴PA=PB,故A选项正确;
在△AOP和△BOP中,
,
∴△AOP≌△BOP(HL),
∴∠APO=∠BPO,OA=OB,故B、C选项正确;
由等腰三角形三线合一的性质,OP垂直平分AB,AB不一定垂直平分OP,故D选项错误.
故选:D.
9.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为从N.现有四个结论:
①CP平分∠ACF;
②∠BPC=∠BAC;
③∠APC=90°﹣∠ABC;
④S△APM+S△CPN>S△APC.
其中结论正确的是( )(填写结论的编号)
A.①②③ B.①②③④ C.②③④ D.①③④
【解答】解:①作PD⊥AC于D,
∵BP平分∠ABC,AP平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上(到角的两边距离相等的点在角的平分线上),
∴CP平分∠ACF,
故①正确;
②∵BP平分∠ABC,CP平分∠ACF,
∴∠ABC=2∠PBC,∠ACF=2∠PCF,
∵∠ACF=∠ABC+∠BAC,∠PCF=∠PBC+∠BPC,
∴∠BAC=2∠BPC,
∴∠BPC=∠BAC,
故②正确;
③∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
∵PM=PN=PD,
∴∠APD=∠MPD,∠CPD=∠NPD,
∴∠APC=∠MPN=90°﹣∠ABC,
故③正确;
④∵AP=AP,PM=PD.CP=CP,PD=PN,
∴Rt△APM≌Rt△APD(HL),Rt△CPN≌Rt△CPD(HL),
∵S△APD=S△APM,S△CPD=S△CPN,
∴S△APM+S△CPN=S△APC,
故④不正确.
综上所述,①②③正确.
故选:A.
10.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:(1)证明:作PH⊥AB于H,
∵AP是∠CAB的平分线,
∴∠PAE=∠PAH,
在△PEA和△PHA中,
,
∴△PEA≌△PHA(AAS),
∴PE=PH,
∵BP平分∠ABD,且PH⊥BA,PF⊥BD,
∴PF=PH,∴PE=PF,∴(1)正确;
(2)与(1)可知:PE=PF,
又∵PE⊥OC于E,PF⊥OD于F,
∴点P在∠COD的平分线上,∴(2)正确;
(3)∵∠O+∠OEP+∠EPF+∠OFP=360°,
又∵∠OEP+∠OFP=90°+90°=180°,
∴∠O+∠EPF=180°,
即∠O+∠EPA+∠HPA+∠HPB+∠FPB=180°,
由(1)知:△PEA≌△PHA,
∴∠EPA=∠HPA,
同理:∠FPB=∠HPB,
∴∠O+2(∠HPA+∠HPB)=180°,即∠O+2∠APB=180°,
∴∠APB=90°﹣,∴(3)错误;
故选:C.
二.填空题
11.如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD于点E,AD=18cm,AB=11cm,那么DE的长度为 3.5 cm.
【解答】解:过C点作CF⊥AB于F,如图,
∵AC平分∠BAD,CE⊥AD,CF⊥AB,
∴CF=CE,
在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AF=AE,
∵∠ABC+∠D=180°,∠ABC+∠CBF=180°,
∴∠CBF=∠D,
在△CBF和△CDE中,
,
∴△CBF≌△CDE(AAS),
∴BF=DE,
∵AF=AE,
∴AB+BF=AD﹣DE,
即11+DE=18﹣DE,
∴DE=3.5cm.
故答案为:3.5.
12.如图所示,已知△ABC的周长是15,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 30 .
【解答】解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC,
∴OE=OD=4,OF=OD=4,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×4×AB+×4×BC+×4×AC
=2(AB+BC+AC)=2×15=30.
故答案为30.
13.如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是 ①②④⑤ (写序号)
【解答】解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,故①正确;
在Rt△ACD和Rt△AED中,,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE,AC=AE,
∴DA平分∠CDE,故②正确;
BE+AC=BE+AE=AB,故④正确;
∵∠BAC+∠B=90°,
∠BDE+∠B=90°,
∴∠BAC=∠BDE,故⑤正确;
∵∠ADE+∠BAD=90°,而∠BAD≠∠B,
∴∠BDE≠∠ADE,
∴DE平分∠ADB错误,故③错误;
综上所述,正确的有①②④⑤.
故答案为:①②④⑤.
14.如图,在△ABC中,两条角平分线相交于点P,过点P作PD⊥BC于点D,若PD=1,△ABC的周长为12,则△ABC的面积为 6 .
【解答】解:连接PA,过点P分别作AB,AC的垂线段PE,PF,
∵BP,CP是△ABC的角平分线,PD⊥BC,
∴PD=PE=PF=1,
∵△ABC的周长为12,
∴AB+BC+AC=12,
∴S△ABC=S△PAB+S△PBC+S△PAC
==
==6,
故答案为:6.
15.如图,△ABC中,AD是∠BAC的平分线,BE是△ABD边AD上的中线,若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是 7.5 .
【解答】解:过点D作DF⊥AB,垂足为F,过点D作DG⊥AC,垂足为G,
∵AD是∠BAC的平分线,DF⊥AB,DG⊥AC,
∴DF=DG,
∵AB=5,AC=3,
∴===,
∵△ABC的面积是24,
∴△ABD的面积=△ABC的面积=×24=15,
∵BE是△ABD边AD上的中线,
∴△ABE的面积=△ABD的面积=7.5,
故答案为:7.5.
16.如图,在四边形ABCD中,∠A=90°,AD=10,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP的最小值为 10 .
【解答】解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,
∴AD=DP,又AD=10,
∴DP=10.
故答案为:10.
三.解答题
17.如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)若AB=20,AC=16,DE=6,求S△ABC.
【解答】解:(1)∵∠B=40°,∠C=76°,
∴∠BAC=180°﹣40°﹣76°=64°,
∵AD是△ABC的角平分线,
∴,
∵DE⊥AB,
∴∠EDA=90°﹣∠DAE=58°.
(2)过点D作DF⊥AC于点F,
∵AD是△ABC的角平分线,DF⊥AC,DE⊥AB,
∴DF=DE=6,
∴.
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
【解答】解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∵∠ABC=60°,∠ACB=40°
∴∠OBC=30°,∠OCB=20°,
∴∠COB=180°﹣(30°+20°)=130°;
(2)过O作OD⊥AB于D点,OE⊥AC于E,OF⊥BC于F,连接AO,如图,
∵∠ABC=60°,OB=4
∴∠OBD=30°,
∴OD=OB=2,
∵∠ABC和∠ACB的平分线相交于点O,
∴OE=OF=OD=2,
∵S△ABC=S△AOB+S△AOC+S△BOC
=×2×AB+×2×AC+×2×BC=AB+BC+AC,
又∵△ABC的周长为16,
∴S△ABC=16.
19.如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
【解答】解:(1)点P是线段CD的中点.理由如下:
过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
(2)过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC.
在△PBE与△PBC中,
,
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
,
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°﹣2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°﹣∠APD=35°.
20.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
【解答】(1)证明:过点O作OM⊥AB,
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2)解:∵在Rt△ABC中,AC=5,BC=12,
∴AB===13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴,
解得:,
∴CE=2,
∴OE=2.
21.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
【解答】(1)证明:
过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴=∠DEB+∠ABC,
∴∠DEB=(∠CDA﹣∠ABC)=∠BAD=30°.
22.如图,△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,EF⊥BC,FM⊥AC,垂足分别是D,F,M,求证:FM=FD.
【解答】证明:作EH⊥AD于H,
则四边形FDFE是矩形,
∴DF=HE,
∵BE平分∠ABC,EF⊥BC,∠BAC=90°,
∴EA=EF,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠HAE=∠MEF,
在△HAE和△MEF中,
,
∴△HAE≌△MEF,
∴EH=MF,
∴FM=FD.
23.如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.
(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:AO平分∠BAC.
(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
【解答】(1)解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC+∠ACB=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°;
(2)证明:过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F,
∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,
∴OD=OE,OD=OF,
∴OE=OF,
∴OA平分∠BAC;
(3)证明:∵OC平分∠ACB,CP平分∠ACD,
∴∠ACO=∠ACB,∠ACP=∠ACD,
∴∠OCP=∠ACO+∠ACP=∠ACB+∠ACD=∠BCD=×180°=90°,
∴OC⊥CP.
24.如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
【解答】(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
25.已知直线EF与直线AB、CD分别交于E、F两点,∠BEF和∠DFE的角平分线交于点P,且∠BEP+∠DFP=90°.
(1)求证:AB∥CD;
(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;
(3)如图3,若∠BEP=60°,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时开始旋转,当射线EP1∥FP2时,求满足条件的t的值为多少.
【解答】解:(1)∵∠BEF和∠DFE的角平分线交于点P,
∴∠EBF=2∠BEP,∠DFE=2∠DFP,
∴∠EBF+∠DFE=2(∠BEP+∠DFP)=2×90°=180°,
∴AB∥CD.
(2)∵∠BEP+∠DFP=90°,又AB∥CD.
∴∠P=180﹣(∠PEF+∠PFE)=180°﹣(∠BEP+∠DFP)=90°,
由外角性质得:∠Q=∠MFQ﹣∠MEQ
=∠MFP﹣∠MEP
=(∠MFP﹣∠MEP)
=,
∵∠P=90°,
∴∠Q==45°.
(3)当FP2在EF右侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t+60°,∠EFP2=3t+30°,
∴15t+60°+3t+30°=180,
解得t=5.
当FP2在EF左侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t﹣60°,∠EFP2=3t﹣30°,
∴15t﹣60°+3t﹣30°=180°,
解得t=15.
综上分析,t=5或t=15时,EP1∥FP2.
一.选择题
1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,CD=3,则△ABD的面积为( )
A.60 B.30 C.15 D.10
2.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P且与AB垂直.若AD=8,BC=10,则△BCP的面积为( )
A.16 B.20 C.40 D.80
3.如图,AD是△ABC中∠BAC的平分线,DE⊥AB,交AB于点E,DF⊥AC,交AC于点F.若S△ABC=7,DE=2,AB=4,则AC的长是( )
A.4 B.3 C.6 D.5
4.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.12 C.8 D.6
5.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是∠ABC的平分线,BE交AD于点F,下面说法:①∠BAD=∠C;②AE=AF;③∠CAD=2∠CBE;④S△BCE=BC AE.其中正确的说法有( )个.
A.1 B.2 C.3 D.4
6.如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO的面积为30,则△ACO的面积为( )
A.18 B.20 C.22 D.24
7.在Rt△ABC中,∠C=90°,小丽进行如图步骤尺规作图,根据操作,对下列判断正确的序号是( )
①AD平分∠BAC
②AD是△ABC的中线
③S△ADC=S△ABD④S△ADC=2S△ADG
A.①②③④ B.③④ C.②③ D.②③④
8.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
9.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为从N.现有四个结论:
①CP平分∠ACF;
②∠BPC=∠BAC;
③∠APC=90°﹣∠ABC;
④S△APM+S△CPN>S△APC.
其中结论正确的是( )(填写结论的编号)
A.①②③ B.①②③④ C.②③④ D.①③④
10.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
11.如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD于点E,AD=18cm,AB=11cm,那么DE的长度为 cm.
12.如图所示,已知△ABC的周长是15,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 .
13.如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是 (写序号)
14.如图,在△ABC中,两条角平分线相交于点P,过点P作PD⊥BC于点D,若PD=1,△ABC的周长为12,则△ABC的面积为 .
15.如图,△ABC中,AD是∠BAC的平分线,BE是△ABD边AD上的中线,若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是 .
16.如图,在四边形ABCD中,∠A=90°,AD=10,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP的最小值为 .
三.解答题
17.如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)若AB=20,AC=16,DE=6,求S△ABC.
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
19.如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
20.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
21.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
22.如图,△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,EF⊥BC,FM⊥AC,垂足分别是D,F,M,求证:FM=FD.
23.如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.
(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:AO平分∠BAC.
(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
24.如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
25.已知直线EF与直线AB、CD分别交于E、F两点,∠BEF和∠DFE的角平分线交于点P,且∠BEP+∠DFP=90°.
(1)求证:AB∥CD;
(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;
(3)如图3,若∠BEP=60°,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时开始旋转,当射线EP1∥FP2时,求满足条件的t的值为多少.
12.3 角的平分线的性质(提升练习)
一.选择题
1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,CD=3,则△ABD的面积为( )
A.60 B.30 C.15 D.10
【解答】解:过点D作DE⊥AB,垂足为E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC=3,
∵AB=10,
∴△ABD的面积=AB DE=×10×3=15,
故选:C.
2.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P且与AB垂直.若AD=8,BC=10,则△BCP的面积为( )
A.16 B.20 C.40 D.80
【解答】解:过P作PE⊥BC于E,
∵AB∥CD,
∴∠BAP+∠CDP=180°,
∵AD⊥AB,
∴∠BAP=90°,∴∠CDP=90°,
即AD⊥CD,
∵PE⊥BC,BP和CP分别平分∠ABC和∠BCD,
∴PA=PE,PE=PD,
∴PA=PD,
∵AD=8,
∴PE=PD=AP=4,
∵BC=10,
∴△BCP的面积为==20.
故选:B.
3.如图,AD是△ABC中∠BAC的平分线,DE⊥AB,交AB于点E,DF⊥AC,交AC于点F.若S△ABC=7,DE=2,AB=4,则AC的长是( )
A.4 B.3 C.6 D.5
【解答】解:∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴7=×4×2+×AC×2,
解得AC=3.
故选:B.
4.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.12 C.8 D.6
【解答】解:过点D作DE⊥BC,交BC于点E,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴DA=DE=3,
∴.
故选:A.
5.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是∠ABC的平分线,BE交AD于点F,下面说法:①∠BAD=∠C;②AE=AF;③∠CAD=2∠CBE;④S△BCE=BC AE.其中正确的说法有( )个.
A.1 B.2 C.3 D.4
【解答】解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠BAC=90°,AD是BC边上的高,
∴∠ABC+∠C=90°,∠CAD+∠C=90°,∠ABD+∠BAD=90°
∴∠ABC=∠CAD,∠C=∠BAD,
∴∠CAD=2∠CBE.
故①③符合题意.
∵∠BAC=90°,AD是BC边上的高,
∴∠ABE+∠AEB=90°,∠CBE+∠BFD=90°,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠BFD=∠AFE,
∴∠AEB=∠AFE,
∴AE=AF.
故②符合题意.
如图,过点E作EP⊥BC于P,
∵∠BAC=90°,BE是∠ABC的平分线,
∴AE=EP,
S△BCE=BC EP=BC AE,
故④符合题意.
故选:D.
6.如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO的面积为30,则△ACO的面积为( )
A.18 B.20 C.22 D.24
【解答】解:∵点O是三条角平分线的交点,
∴点O到AB,AC的距离相等,
∴△AOB、△AOC面积的比=AB:AC=10:8=5:4.
∵△ABO的面积为30,
∴△ACO的面积为24.
故选:D.
7.在Rt△ABC中,∠C=90°,小丽进行如图步骤尺规作图,根据操作,对下列判断正确的序号是( )
①AD平分∠BAC
②AD是△ABC的中线
③S△ADC=S△ABD④S△ADC=2S△ADG
A.①②③④ B.③④ C.②③ D.②③④
【解答】解:由作法得DG垂直平分BC,
∴DG⊥BC,BD=CD,
∴AD为△ABC的中线,所以①错误;
∵EF是线段BC的垂直平分线,
∴D是线段BC的中点,
∴AD是△ABC的中线,所以②正确;
∵∠C=90°,
∴DG∥AC,
∴DG为△ABC的中位线,
∴AC=2DG,
BG=AG,
∴S△ADC=S△ABD,所以③正确;
S△ADG=S△BDG,
∴S△ADC=2S△ADG,所以④正确.
故选:D.
8.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
【解答】解:∵OP平分∠AOB,PA⊥OA,PB⊥OB,
∴PA=PB,故A选项正确;
在△AOP和△BOP中,
,
∴△AOP≌△BOP(HL),
∴∠APO=∠BPO,OA=OB,故B、C选项正确;
由等腰三角形三线合一的性质,OP垂直平分AB,AB不一定垂直平分OP,故D选项错误.
故选:D.
9.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为从N.现有四个结论:
①CP平分∠ACF;
②∠BPC=∠BAC;
③∠APC=90°﹣∠ABC;
④S△APM+S△CPN>S△APC.
其中结论正确的是( )(填写结论的编号)
A.①②③ B.①②③④ C.②③④ D.①③④
【解答】解:①作PD⊥AC于D,
∵BP平分∠ABC,AP平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上(到角的两边距离相等的点在角的平分线上),
∴CP平分∠ACF,
故①正确;
②∵BP平分∠ABC,CP平分∠ACF,
∴∠ABC=2∠PBC,∠ACF=2∠PCF,
∵∠ACF=∠ABC+∠BAC,∠PCF=∠PBC+∠BPC,
∴∠BAC=2∠BPC,
∴∠BPC=∠BAC,
故②正确;
③∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
∵PM=PN=PD,
∴∠APD=∠MPD,∠CPD=∠NPD,
∴∠APC=∠MPN=90°﹣∠ABC,
故③正确;
④∵AP=AP,PM=PD.CP=CP,PD=PN,
∴Rt△APM≌Rt△APD(HL),Rt△CPN≌Rt△CPD(HL),
∵S△APD=S△APM,S△CPD=S△CPN,
∴S△APM+S△CPN=S△APC,
故④不正确.
综上所述,①②③正确.
故选:A.
10.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:(1)证明:作PH⊥AB于H,
∵AP是∠CAB的平分线,
∴∠PAE=∠PAH,
在△PEA和△PHA中,
,
∴△PEA≌△PHA(AAS),
∴PE=PH,
∵BP平分∠ABD,且PH⊥BA,PF⊥BD,
∴PF=PH,∴PE=PF,∴(1)正确;
(2)与(1)可知:PE=PF,
又∵PE⊥OC于E,PF⊥OD于F,
∴点P在∠COD的平分线上,∴(2)正确;
(3)∵∠O+∠OEP+∠EPF+∠OFP=360°,
又∵∠OEP+∠OFP=90°+90°=180°,
∴∠O+∠EPF=180°,
即∠O+∠EPA+∠HPA+∠HPB+∠FPB=180°,
由(1)知:△PEA≌△PHA,
∴∠EPA=∠HPA,
同理:∠FPB=∠HPB,
∴∠O+2(∠HPA+∠HPB)=180°,即∠O+2∠APB=180°,
∴∠APB=90°﹣,∴(3)错误;
故选:C.
二.填空题
11.如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD于点E,AD=18cm,AB=11cm,那么DE的长度为 3.5 cm.
【解答】解:过C点作CF⊥AB于F,如图,
∵AC平分∠BAD,CE⊥AD,CF⊥AB,
∴CF=CE,
在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AF=AE,
∵∠ABC+∠D=180°,∠ABC+∠CBF=180°,
∴∠CBF=∠D,
在△CBF和△CDE中,
,
∴△CBF≌△CDE(AAS),
∴BF=DE,
∵AF=AE,
∴AB+BF=AD﹣DE,
即11+DE=18﹣DE,
∴DE=3.5cm.
故答案为:3.5.
12.如图所示,已知△ABC的周长是15,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 30 .
【解答】解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC,
∴OE=OD=4,OF=OD=4,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×4×AB+×4×BC+×4×AC
=2(AB+BC+AC)=2×15=30.
故答案为30.
13.如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是 ①②④⑤ (写序号)
【解答】解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,故①正确;
在Rt△ACD和Rt△AED中,,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE,AC=AE,
∴DA平分∠CDE,故②正确;
BE+AC=BE+AE=AB,故④正确;
∵∠BAC+∠B=90°,
∠BDE+∠B=90°,
∴∠BAC=∠BDE,故⑤正确;
∵∠ADE+∠BAD=90°,而∠BAD≠∠B,
∴∠BDE≠∠ADE,
∴DE平分∠ADB错误,故③错误;
综上所述,正确的有①②④⑤.
故答案为:①②④⑤.
14.如图,在△ABC中,两条角平分线相交于点P,过点P作PD⊥BC于点D,若PD=1,△ABC的周长为12,则△ABC的面积为 6 .
【解答】解:连接PA,过点P分别作AB,AC的垂线段PE,PF,
∵BP,CP是△ABC的角平分线,PD⊥BC,
∴PD=PE=PF=1,
∵△ABC的周长为12,
∴AB+BC+AC=12,
∴S△ABC=S△PAB+S△PBC+S△PAC
==
==6,
故答案为:6.
15.如图,△ABC中,AD是∠BAC的平分线,BE是△ABD边AD上的中线,若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是 7.5 .
【解答】解:过点D作DF⊥AB,垂足为F,过点D作DG⊥AC,垂足为G,
∵AD是∠BAC的平分线,DF⊥AB,DG⊥AC,
∴DF=DG,
∵AB=5,AC=3,
∴===,
∵△ABC的面积是24,
∴△ABD的面积=△ABC的面积=×24=15,
∵BE是△ABD边AD上的中线,
∴△ABE的面积=△ABD的面积=7.5,
故答案为:7.5.
16.如图,在四边形ABCD中,∠A=90°,AD=10,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP的最小值为 10 .
【解答】解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,
∴AD=DP,又AD=10,
∴DP=10.
故答案为:10.
三.解答题
17.如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)若AB=20,AC=16,DE=6,求S△ABC.
【解答】解:(1)∵∠B=40°,∠C=76°,
∴∠BAC=180°﹣40°﹣76°=64°,
∵AD是△ABC的角平分线,
∴,
∵DE⊥AB,
∴∠EDA=90°﹣∠DAE=58°.
(2)过点D作DF⊥AC于点F,
∵AD是△ABC的角平分线,DF⊥AC,DE⊥AB,
∴DF=DE=6,
∴.
18.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
【解答】解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∵∠ABC=60°,∠ACB=40°
∴∠OBC=30°,∠OCB=20°,
∴∠COB=180°﹣(30°+20°)=130°;
(2)过O作OD⊥AB于D点,OE⊥AC于E,OF⊥BC于F,连接AO,如图,
∵∠ABC=60°,OB=4
∴∠OBD=30°,
∴OD=OB=2,
∵∠ABC和∠ACB的平分线相交于点O,
∴OE=OF=OD=2,
∵S△ABC=S△AOB+S△AOC+S△BOC
=×2×AB+×2×AC+×2×BC=AB+BC+AC,
又∵△ABC的周长为16,
∴S△ABC=16.
19.如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
【解答】解:(1)点P是线段CD的中点.理由如下:
过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
(2)过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC.
在△PBE与△PBC中,
,
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
,
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°﹣2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°﹣∠APD=35°.
20.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
【解答】(1)证明:过点O作OM⊥AB,
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2)解:∵在Rt△ABC中,AC=5,BC=12,
∴AB===13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴,
解得:,
∴CE=2,
∴OE=2.
21.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
【解答】(1)证明:
过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴=∠DEB+∠ABC,
∴∠DEB=(∠CDA﹣∠ABC)=∠BAD=30°.
22.如图,△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,EF⊥BC,FM⊥AC,垂足分别是D,F,M,求证:FM=FD.
【解答】证明:作EH⊥AD于H,
则四边形FDFE是矩形,
∴DF=HE,
∵BE平分∠ABC,EF⊥BC,∠BAC=90°,
∴EA=EF,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠HAE=∠MEF,
在△HAE和△MEF中,
,
∴△HAE≌△MEF,
∴EH=MF,
∴FM=FD.
23.如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.
(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:AO平分∠BAC.
(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
【解答】(1)解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC+∠ACB=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°;
(2)证明:过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F,
∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,
∴OD=OE,OD=OF,
∴OE=OF,
∴OA平分∠BAC;
(3)证明:∵OC平分∠ACB,CP平分∠ACD,
∴∠ACO=∠ACB,∠ACP=∠ACD,
∴∠OCP=∠ACO+∠ACP=∠ACB+∠ACD=∠BCD=×180°=90°,
∴OC⊥CP.
24.如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
【解答】(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
25.已知直线EF与直线AB、CD分别交于E、F两点,∠BEF和∠DFE的角平分线交于点P,且∠BEP+∠DFP=90°.
(1)求证:AB∥CD;
(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;
(3)如图3,若∠BEP=60°,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时开始旋转,当射线EP1∥FP2时,求满足条件的t的值为多少.
【解答】解:(1)∵∠BEF和∠DFE的角平分线交于点P,
∴∠EBF=2∠BEP,∠DFE=2∠DFP,
∴∠EBF+∠DFE=2(∠BEP+∠DFP)=2×90°=180°,
∴AB∥CD.
(2)∵∠BEP+∠DFP=90°,又AB∥CD.
∴∠P=180﹣(∠PEF+∠PFE)=180°﹣(∠BEP+∠DFP)=90°,
由外角性质得:∠Q=∠MFQ﹣∠MEQ
=∠MFP﹣∠MEP
=(∠MFP﹣∠MEP)
=,
∵∠P=90°,
∴∠Q==45°.
(3)当FP2在EF右侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t+60°,∠EFP2=3t+30°,
∴15t+60°+3t+30°=180,
解得t=5.
当FP2在EF左侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t﹣60°,∠EFP2=3t﹣30°,
∴15t﹣60°+3t﹣30°=180°,
解得t=15.
综上分析,t=5或t=15时,EP1∥FP2.
