新人教版5年级上册 3.6 循环小数 教学课件(35张PPT)
文档属性
| 名称 | 新人教版5年级上册 3.6 循环小数 教学课件(35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 29.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-30 15:07:32 | ||
图片预览











文档简介
(共35张PPT)
3.6 循环小数
第三单元 小数除法
新人教版五年级上册
教学目标
1.学习目标描述:理解循环小数、有限小数、无限小数和循环节的意义,能用简便记法表示循环小数。经历循环小数的探究过程,培养观察、比较、分析与概括的能力。
2.学习内容分析:引导探究商循环出现的原因是因为余数重复出现,理解循环小数的意义。在计算的基础上,观察比较两道例题的商,使学生看到循环小数的两种情况。通过自学方式,学会循环节和循环小数的简便记法。
在合作探究中,以算一算、想一想的方式理解有限小数和无限小数。
3.学习核心素养分析:在学习过程中,感受数学知识的无穷奥秘,体验发现知识的快乐,激发学习的兴趣。
从前有座山,
山上有座庙,
庙里有个老和尚,
他对小和尚说,
从前有座山,
山上有座庙,
庙里有个老和尚,
他对小和尚说
......
从前有座山,
山上有座庙,
庙里有个老和尚,
他对小和尚说,
依次不断地重复
课前导入
春
夏
秋
冬
课前导入
白天黑夜交替出现
课前导入
一个星期的七天的排列顺序,
一年12个月的排序,
……
像这样“依次不断重复出现”的现象叫做“循环”。
在数学中也存在这样的“循环”现象。
课前导入
怎样列式?
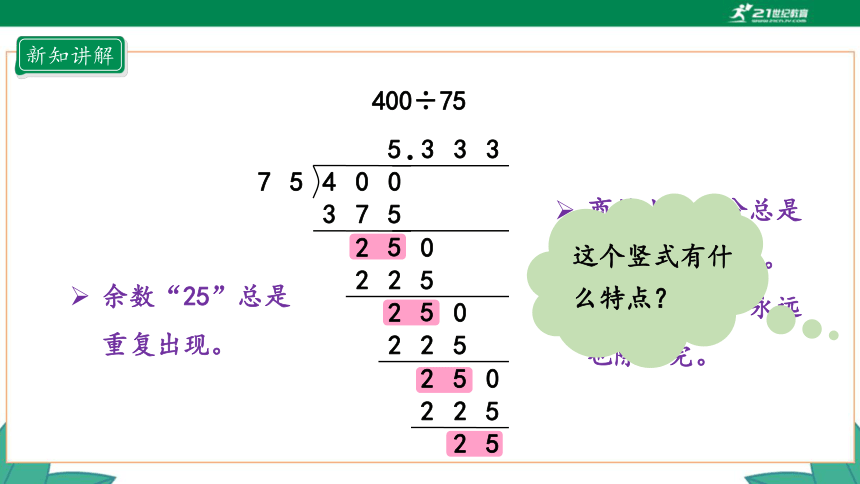
400÷75
王鹏跑400 m用时75秒,他平均每秒跑多少米?
新知讲解
探
究
活
动
列竖式计算400÷75。
观察竖式计算的过程,看看你有什么发现?
小组交流你的发现,看看谁说得又对又全。
想一想:怎样表示这种“永远也除不完”的商?这样的商有什么特点?
新知讲解
5
5
400÷75
5
7
5
4
0
0
3
7
5
5
2
0
2
2
5
2
0
2
2
5
2
0
2
2
5
2
5
3
3
3
商的小数部分总是重复出现“3”。
继续除下去,永远也除不完。
余数“25”总是重复出现。
这个竖式有什么特点?
新知讲解
小
组
交
流
设问:为什么商的小数部分总是重复出现“3”?
它和每次出现的余数有什么关系?
猜想:如果继续除下去,商的第四位小数是多少?
第五位呢?
验证:接着往下除,看看你的猜想对不对。
反思:我们可以怎样表示400÷75的商?
新知讲解
400÷75
=5.333…
表示永远也除不完的商
5
5
5
7
5
4
0
0
3
7
5
5
2
0
2
2
5
2
0
2
2
5
2
0
2
2
5
2
5
3
3
3
新知讲解
28÷18=
78.6÷11=
探究活动
1.列竖式计算这两个算式,计算到商的第三位小数。
2.观察每一步计算的余数,看看有什么特点。
3.继续除出两位小数,与前几步比较,猜一猜继续除下去,商会怎样。
新知讲解
0
0
1
1
8
2
8
1
8
0
0
1
9
0
1
0
0
9
0
1
9
0
1
0
28÷18=
5
5
5
1.555…
还需要继续往下除吗?为什么?
新知讲解
78.6÷11=
7.14545…
像这样的算式除到哪一位就可以不除了?
7
1
1
1
7
8
6
7
7
6
1
1
1
0
0
5
4
4
6
5
5
5
0
0
0
5
4
4
6
5
5
5
4
5
4
5
新知讲解
5.333…
1.555…
7.14545…
这些商有什么特点?
小数部分从第一位起,数字“3”依次不断重复出现。
小数部分从第一位起,数字“5”依次不断重复出现。
小数部分从第二位起,数字“45”依次不断重复出现。
尝试写出几个循环小数,同桌互相判断写的是否正确。
循环小数
新知讲解
5.333…
1.555…
7.14545…
一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫作循环小数。
什么是循环小数?
新知讲解
自
学
指
导
自学教材第34页“做一做”以上内容,思考问题:
(1)什么是循环节?
(2)怎样用简便方法表示循环小数?
(3)尝试找出下面几个小数的循环节,并用简便
形式写出它们。
9.999… 0.586586… 5.23636…
新知讲解
9.999…
0.586586…
5.23636…
一个循环小数的小数部分,
依次不断重复出现的数字,
就是这个循环小数的循环节。
什么是循环节?
循环节是9
循环节是586
循环节是36
新知讲解
9.999…
0.586586…
5.23636…
读作:九点九,九循环
写作:
读作:零点五八六,五八六循环
写作:
读作:五点二三六,三六循环
写作:
你会读循环小数吗?
新知讲解
15÷16=
1.5÷7=
探究活动
1.列竖式计算这两个算式。
2.观察这两个算式的商,想一想:
两个数相除,如果不能得到整数商,所得的商会有
哪些情况?
新知讲解
15÷16=
1.5÷7=
0.9375
小数部分的位数有限的小数是有限小数。
小数部分的位数无限的小数是无限小数。
新知讲解
小
组
交
流
循环小数是有限小数还是无限小数?为什么?
循环小数、有限小数和无限小数之间的关系是怎样的?
新知讲解
循环小数、有限小数和无限小数之间的关系
小数
有限小数
无限小数
循环小数
无限不循环小数
新知讲解
1.填一填。
(1)像0.555…、2.3636…、3.2534534…那样,从小数部分的某一位起,一个数字或几个数字(
),这样的小数叫作循环小数。
知识点1
认识循环小数
依次不断
重复出现
课堂练习
(2)循环小数0.555…、2.3636…、3.2534534…的循环节分别是( )、( )和( )。
5
36
534
解析:一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。
新知讲解
(3)用循环小数的简便记法表示下面各小数。
0.999…( ) 0.450450…( )
1.13838…( ) 2.37543754…( )
0.9
0.450
1.138
2.3754
解析:写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个圆点。
新知讲解
(4)求循环小数的近似数。(保留两位小数)
2.9494…≈( ) 0.0183≈( )
0.999…≈( ) 7.275≈( )
2.95
0.02
1.00
7.28
解析:0.999…保留两位小数,因为千分位是9,所以需向百分位进1,百分位上的9加上进上来的1,是10,需再向十分位进1,十分位上的9加上进上来的1,是10,需再向个位进1,所以0.999…保留两位小数是1.00。
新知讲解
2.分一分。
知识点2
认识有限小数和无限小数
新知讲解
有限小数: _____________________________。
无限小数: _____________________________
_____________。
循环小数: _____________________________。
3.1515、8.4、1.777、0.54
7.385612…、6.1、2.333…、
6.1、2.333…、0.212、4.916
0.212、4.916
解析:根据有限小数、无限小数、循环小数的定义分类。
新知讲解
3.3÷14的商的小数部分第100位上的数字是几?前50位上的数字的和是多少?
提升点1
循环小数中的周期问题
3÷14=0.2142857
(100-1)÷6=16……3 (50-1)÷6=8……1
(1+4+2+8+5+7)×8+2+1=219
答:3÷14的商的小数部分第100位上的数字是2,前50位上的数字的和是219。
新知讲解
解析:本题考查的知识点是循环小数。
3÷14=0.2142857,十分位后以142857为一个组合无限循环。(100-1)÷6=16……3,第100位上的数字是第17个循环节中的第3个数字,即2。
(50-1)÷6=8……1,第50位上的数字是第9个循环节中的第1个数字,即1,所以商的前50位上的数字的和是(1+4+2+8+5+7)×8+2+1=219。
新知讲解
4.梦梦在比较循环小数的大小时,把循环节上面的小圆点漏写了,写成了下面的不等式,请补上小圆点使不等式成立。(每个数都是循环小数)
2.3435<2.3435<2.3435<2.3435
提升点2
根据排列顺序确定循环节
新知讲解
解析:根据写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个圆
点,可以得到四个循环小数:2.3435,2.3435,2.3435,2.3435。再根据小数大小比较的方法得出结果。
2.3435<2.3435<2.3435<2.3435
新知讲解
在小数1.80528102007上加两个循环点,能得到的最小的循环小数是多少?最大的循环小数是多少?请写出来。
最小:1.80528102007
最大:1.80528102007
新知讲解
点拨:要求最小的循环小数,首先找出小数部分最小的数字为0,再看0后面一位上的数字,有5、2、0、7。其中0最小,所以最小的循环小数是1.80528102007;要求最大的循环小数,首先找出小数部分最大的数字为8,再看8后面一位上的数
字,有0、1。其中1较大,所以最大的循环小数是1.80528102007。
新知讲解
3.6 循环小数
第三单元 小数除法
新人教版五年级上册
教学目标
1.学习目标描述:理解循环小数、有限小数、无限小数和循环节的意义,能用简便记法表示循环小数。经历循环小数的探究过程,培养观察、比较、分析与概括的能力。
2.学习内容分析:引导探究商循环出现的原因是因为余数重复出现,理解循环小数的意义。在计算的基础上,观察比较两道例题的商,使学生看到循环小数的两种情况。通过自学方式,学会循环节和循环小数的简便记法。
在合作探究中,以算一算、想一想的方式理解有限小数和无限小数。
3.学习核心素养分析:在学习过程中,感受数学知识的无穷奥秘,体验发现知识的快乐,激发学习的兴趣。
从前有座山,
山上有座庙,
庙里有个老和尚,
他对小和尚说,
从前有座山,
山上有座庙,
庙里有个老和尚,
他对小和尚说
......
从前有座山,
山上有座庙,
庙里有个老和尚,
他对小和尚说,
依次不断地重复
课前导入
春
夏
秋
冬
课前导入
白天黑夜交替出现
课前导入
一个星期的七天的排列顺序,
一年12个月的排序,
……
像这样“依次不断重复出现”的现象叫做“循环”。
在数学中也存在这样的“循环”现象。
课前导入
怎样列式?
400÷75
王鹏跑400 m用时75秒,他平均每秒跑多少米?
新知讲解
探
究
活
动
列竖式计算400÷75。
观察竖式计算的过程,看看你有什么发现?
小组交流你的发现,看看谁说得又对又全。
想一想:怎样表示这种“永远也除不完”的商?这样的商有什么特点?
新知讲解
5
5
400÷75
5
7
5
4
0
0
3
7
5
5
2
0
2
2
5
2
0
2
2
5
2
0
2
2
5
2
5
3
3
3
商的小数部分总是重复出现“3”。
继续除下去,永远也除不完。
余数“25”总是重复出现。
这个竖式有什么特点?
新知讲解
小
组
交
流
设问:为什么商的小数部分总是重复出现“3”?
它和每次出现的余数有什么关系?
猜想:如果继续除下去,商的第四位小数是多少?
第五位呢?
验证:接着往下除,看看你的猜想对不对。
反思:我们可以怎样表示400÷75的商?
新知讲解
400÷75
=5.333…
表示永远也除不完的商
5
5
5
7
5
4
0
0
3
7
5
5
2
0
2
2
5
2
0
2
2
5
2
0
2
2
5
2
5
3
3
3
新知讲解
28÷18=
78.6÷11=
探究活动
1.列竖式计算这两个算式,计算到商的第三位小数。
2.观察每一步计算的余数,看看有什么特点。
3.继续除出两位小数,与前几步比较,猜一猜继续除下去,商会怎样。
新知讲解
0
0
1
1
8
2
8
1
8
0
0
1
9
0
1
0
0
9
0
1
9
0
1
0
28÷18=
5
5
5
1.555…
还需要继续往下除吗?为什么?
新知讲解
78.6÷11=
7.14545…
像这样的算式除到哪一位就可以不除了?
7
1
1
1
7
8
6
7
7
6
1
1
1
0
0
5
4
4
6
5
5
5
0
0
0
5
4
4
6
5
5
5
4
5
4
5
新知讲解
5.333…
1.555…
7.14545…
这些商有什么特点?
小数部分从第一位起,数字“3”依次不断重复出现。
小数部分从第一位起,数字“5”依次不断重复出现。
小数部分从第二位起,数字“45”依次不断重复出现。
尝试写出几个循环小数,同桌互相判断写的是否正确。
循环小数
新知讲解
5.333…
1.555…
7.14545…
一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫作循环小数。
什么是循环小数?
新知讲解
自
学
指
导
自学教材第34页“做一做”以上内容,思考问题:
(1)什么是循环节?
(2)怎样用简便方法表示循环小数?
(3)尝试找出下面几个小数的循环节,并用简便
形式写出它们。
9.999… 0.586586… 5.23636…
新知讲解
9.999…
0.586586…
5.23636…
一个循环小数的小数部分,
依次不断重复出现的数字,
就是这个循环小数的循环节。
什么是循环节?
循环节是9
循环节是586
循环节是36
新知讲解
9.999…
0.586586…
5.23636…
读作:九点九,九循环
写作:
读作:零点五八六,五八六循环
写作:
读作:五点二三六,三六循环
写作:
你会读循环小数吗?
新知讲解
15÷16=
1.5÷7=
探究活动
1.列竖式计算这两个算式。
2.观察这两个算式的商,想一想:
两个数相除,如果不能得到整数商,所得的商会有
哪些情况?
新知讲解
15÷16=
1.5÷7=
0.9375
小数部分的位数有限的小数是有限小数。
小数部分的位数无限的小数是无限小数。
新知讲解
小
组
交
流
循环小数是有限小数还是无限小数?为什么?
循环小数、有限小数和无限小数之间的关系是怎样的?
新知讲解
循环小数、有限小数和无限小数之间的关系
小数
有限小数
无限小数
循环小数
无限不循环小数
新知讲解
1.填一填。
(1)像0.555…、2.3636…、3.2534534…那样,从小数部分的某一位起,一个数字或几个数字(
),这样的小数叫作循环小数。
知识点1
认识循环小数
依次不断
重复出现
课堂练习
(2)循环小数0.555…、2.3636…、3.2534534…的循环节分别是( )、( )和( )。
5
36
534
解析:一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。
新知讲解
(3)用循环小数的简便记法表示下面各小数。
0.999…( ) 0.450450…( )
1.13838…( ) 2.37543754…( )
0.9
0.450
1.138
2.3754
解析:写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个圆点。
新知讲解
(4)求循环小数的近似数。(保留两位小数)
2.9494…≈( ) 0.0183≈( )
0.999…≈( ) 7.275≈( )
2.95
0.02
1.00
7.28
解析:0.999…保留两位小数,因为千分位是9,所以需向百分位进1,百分位上的9加上进上来的1,是10,需再向十分位进1,十分位上的9加上进上来的1,是10,需再向个位进1,所以0.999…保留两位小数是1.00。
新知讲解
2.分一分。
知识点2
认识有限小数和无限小数
新知讲解
有限小数: _____________________________。
无限小数: _____________________________
_____________。
循环小数: _____________________________。
3.1515、8.4、1.777、0.54
7.385612…、6.1、2.333…、
6.1、2.333…、0.212、4.916
0.212、4.916
解析:根据有限小数、无限小数、循环小数的定义分类。
新知讲解
3.3÷14的商的小数部分第100位上的数字是几?前50位上的数字的和是多少?
提升点1
循环小数中的周期问题
3÷14=0.2142857
(100-1)÷6=16……3 (50-1)÷6=8……1
(1+4+2+8+5+7)×8+2+1=219
答:3÷14的商的小数部分第100位上的数字是2,前50位上的数字的和是219。
新知讲解
解析:本题考查的知识点是循环小数。
3÷14=0.2142857,十分位后以142857为一个组合无限循环。(100-1)÷6=16……3,第100位上的数字是第17个循环节中的第3个数字,即2。
(50-1)÷6=8……1,第50位上的数字是第9个循环节中的第1个数字,即1,所以商的前50位上的数字的和是(1+4+2+8+5+7)×8+2+1=219。
新知讲解
4.梦梦在比较循环小数的大小时,把循环节上面的小圆点漏写了,写成了下面的不等式,请补上小圆点使不等式成立。(每个数都是循环小数)
2.3435<2.3435<2.3435<2.3435
提升点2
根据排列顺序确定循环节
新知讲解
解析:根据写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个圆
点,可以得到四个循环小数:2.3435,2.3435,2.3435,2.3435。再根据小数大小比较的方法得出结果。
2.3435<2.3435<2.3435<2.3435
新知讲解
在小数1.80528102007上加两个循环点,能得到的最小的循环小数是多少?最大的循环小数是多少?请写出来。
最小:1.80528102007
最大:1.80528102007
新知讲解
点拨:要求最小的循环小数,首先找出小数部分最小的数字为0,再看0后面一位上的数字,有5、2、0、7。其中0最小,所以最小的循环小数是1.80528102007;要求最大的循环小数,首先找出小数部分最大的数字为8,再看8后面一位上的数
字,有0、1。其中1较大,所以最大的循环小数是1.80528102007。
新知讲解
