第4章几何图形初步 检测题(有答案)2023-2024学年度人教版数学七年级上册
文档属性
| 名称 | 第4章几何图形初步 检测题(有答案)2023-2024学年度人教版数学七年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 405.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 00:00:00 | ||
图片预览




文档简介
第4章检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
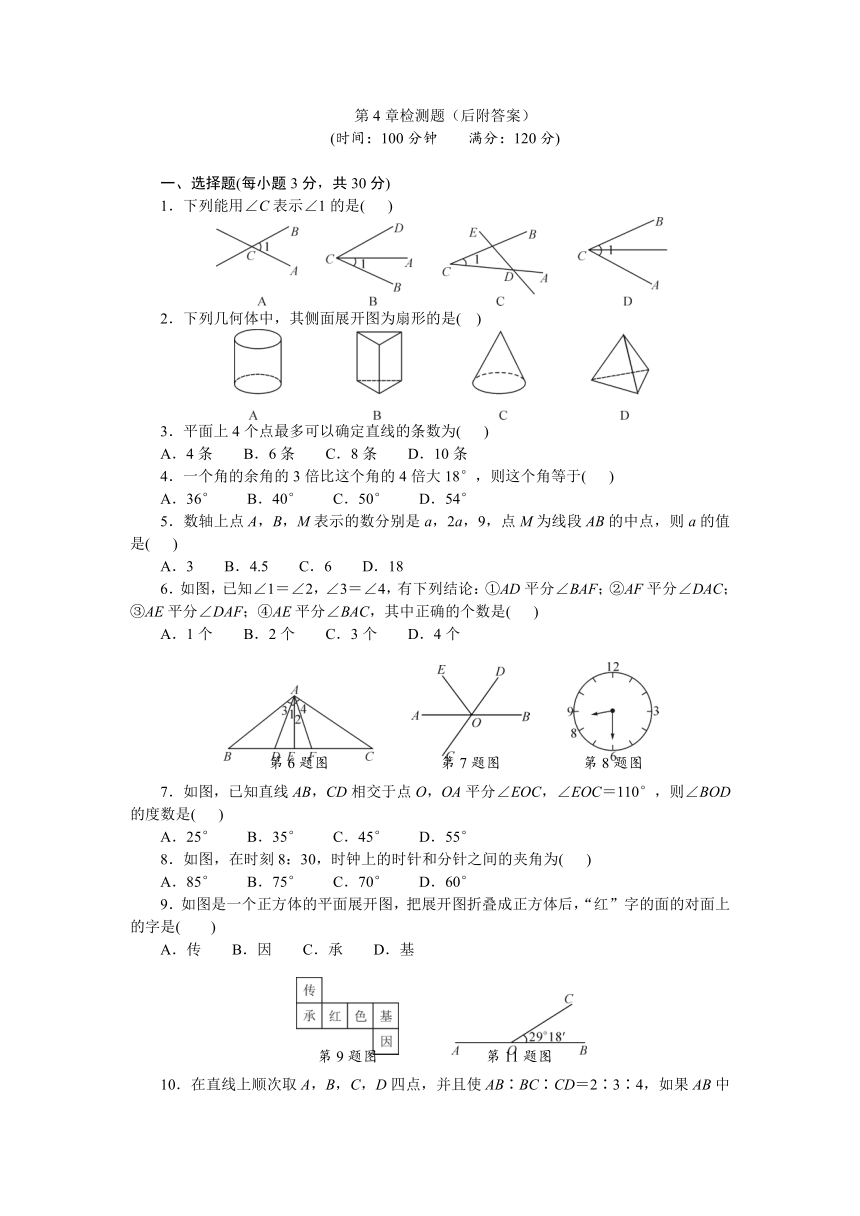
1.下列能用∠C表示∠1的是( )
2.下列几何体中,其侧面展开图为扇形的是( )
3.平面上4个点最多可以确定直线的条数为( )
A.4条 B.6条 C.8条 D.10条
4.一个角的余角的3倍比这个角的4倍大18°,则这个角等于( )
A.36° B.40° C.50° D.54°
5.数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( )
A.3 B.4.5 C.6 D.18
6.如图,已知∠1=∠2,∠3=∠4,有下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AE平分∠BAC,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第7题图)) eq \o(\s\up7(),\s\do5(第8题图))
7.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
8.如图,在时刻8:30,时钟上的时针和分针之间的夹角为( )
A.85° B.75° C.70° D.60°
9.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( )
A.传 B.因 C.承 D.基
eq \o(\s\up7(),\s\do5(第9题图)) eq \o(\s\up7(),\s\do5(第11题图))
10.在直线上顺次取A,B,C,D四点,并且使AB∶BC∶CD=2∶3∶4,如果AB中点M与CD中点N的距离是12 cm,那么CD的长是( )
A.4 cm B.6 cm C.8 cm D.24 cm
二、填空题(每小题3分,共15分)
11.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为____.
12.如图,数轴上A,B两点所表示的数分别是-4和2,点C是线段AB的中点,则点C所表示的数是__ _.
13.计算:(1)53°19′42″+16°40′18″=__ __;
(2)23°15′16″×5=__ __.
14.如图是由一副三角板拼成的两个图形,则:
(1)在第一个图形中,∠ACD=__ __,∠ABD=__ _;
(2)在第二个图形中,∠BAG=__ __,∠AGC=__ __.
15.已知A,B,C三点都在数轴上,点A在数轴上对应的数为2,且AB=5,BC=3,则点C在数轴上对应的数为__ __.
三、解答题(共75分)
16.(8分)如图是由七块相同的小正方体搭成的立体图形,请画出这个图形分别从正面看、从左面看和从上面看得到的平面图形.
17.(9分)已知∠1与∠2互为补角,∠2的度数的一半比∠1大45°,求∠1与∠2的度数.
18.(9分)画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个点?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
19.(9分)如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=AB,点E是AC的中点,点D是AB的中点,求DE的长.
20.(9分)如图,点M在线段AB上,线段BM与AM的长度之比为5∶4,点N为线段AM的中点.
(1)若AB=27 cm,求BN的长.
(2)在线段AB上作出一点E,满足MB=3EB,若ME=t,求AB的长(用含t的代数式表示).
21.(10分)如图,点A,O,B在同一条直线上,∠COB与∠BOD互余,OE,OF分别是∠AOC,∠AOD的平分线,求∠EOF的度数.
22.(10分)如图,将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由.
23.(11分)探索新知:
如图①,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线________这个角的“巧分线”;(填“是”或“不是”)
(2)如图②,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=________;(用含α的代数式表示)
深入研究:
(3)如图②,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请求出当射线PQ是∠MPN的“巧分线”时t的值.
答案:
第4章检测题(教师版)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列能用∠C表示∠1的是( C )
2.下列几何体中,其侧面展开图为扇形的是( C )
3.平面上4个点最多可以确定直线的条数为( B )
A.4条 B.6条 C.8条 D.10条
4.一个角的余角的3倍比这个角的4倍大18°,则这个角等于( A )
A.36° B.40° C.50° D.54°
5.数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( C )
A.3 B.4.5 C.6 D.18
6.如图,已知∠1=∠2,∠3=∠4,有下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AE平分∠BAC,其中正确的个数是( B )
A.1个 B.2个 C.3个 D.4个
eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第7题图)) eq \o(\s\up7(),\s\do5(第8题图))
7.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( D )
A.25° B.35° C.45° D.55°
8.如图,在时刻8:30,时钟上的时针和分针之间的夹角为( B )
A.85° B.75° C.70° D.60°
9.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( D )
A.传 B.因 C.承 D.基
eq \o(\s\up7(),\s\do5(第9题图)) eq \o(\s\up7(),\s\do5(第11题图))
10.在直线上顺次取A,B,C,D四点,并且使AB∶BC∶CD=2∶3∶4,如果AB中点M与CD中点N的距离是12 cm,那么CD的长是( C )
A.4 cm B.6 cm C.8 cm D.24 cm
二、填空题(每小题3分,共15分)
11.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为__150°42′__.
12.如图,数轴上A,B两点所表示的数分别是-4和2,点C是线段AB的中点,则点C所表示的数是__-1__.
13.计算:(1)53°19′42″+16°40′18″=__70°__;
(2)23°15′16″×5=__116°16′20″__.
14.如图是由一副三角板拼成的两个图形,则:
(1)在第一个图形中,∠ACD=__75°__,∠ABD=__135°__;
(2)在第二个图形中,∠BAG=__45°__,∠AGC=__105°__.
15.已知A,B,C三点都在数轴上,点A在数轴上对应的数为2,且AB=5,BC=3,则点C在数轴上对应的数为__-6或0或4或10__.
三、解答题(共75分)
16.(8分)如图是由七块相同的小正方体搭成的立体图形,请画出这个图形分别从正面看、从左面看和从上面看得到的平面图形.
解:
17.(9分)已知∠1与∠2互为补角,∠2的度数的一半比∠1大45°,求∠1与∠2的度数.
解:∠1=30°,∠2=150°
18.(9分)画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个点?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
解:(1)如图:
(2)线段DC的中点是点A,AB=CD (3)因为BC=AB=×2=1 (cm),所以AC=AB+BC=2+1=3 (cm).又因为AD=AC=3 cm,所以BD=DA+AB=3+2=5 (cm)
19.(9分)如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=AB,点E是AC的中点,点D是AB的中点,求DE的长.
解:因为AB=24 cm,BC=AB=
×24=9(cm),所以AC=33 cm,又因为E是AC的中点,则AE=AC=16.5 cm,又因为D是AB的中点,则AD=AB=12 cm,所以DE=AE-AD=16.5-12=4.5(cm)
20.(9分)如图,点M在线段AB上,线段BM与AM的长度之比为5∶4,点N为线段AM的中点.
(1)若AB=27 cm,求BN的长.
(2)在线段AB上作出一点E,满足MB=3EB,若ME=t,求AB的长(用含t的代数式表示).
解:(1)由题知BM∶AM=5∶4,设BM=5x cm,AM=4x cm,∴AB=BM+AM=9x cm,∵AB=27 cm,∴9x=27,∴x=3.∴AM=12 cm,BM=15 cm.∵点N是线段AM的中点,∴MN=AM=6 cm,∴BN=BM+MN=15+6=21(cm) (2)∵BM∶AM=5∶4,∴AM=BM,∵BM=3EB,∴ME=BM=t,∴BM=t,∵AB=AM+BM=BM+BM=BM,∴AB=×t=t
21.(10分)如图,点A,O,B在同一条直线上,∠COB与∠BOD互余,OE,OF分别是∠AOC,∠AOD的平分线,求∠EOF的度数.
解:由∠COB与∠BOD互余得∠COD=90°,所以∠AOC+∠AOD=360°-90°=270°,又因为OE,OF分别是∠AOC,∠AOD的平分线,所以∠EOF=(∠AOC+∠AOD)=×270°=135°
22.(10分)如图,将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由.
解:(1)∠ACE=∠BCD,理由略 (2)因为∠DCE=30°,∠ACD=90°,∴∠ACE=∠ACD-∠DCE=90°-30°=60°,所以∠ACB=∠ACE+∠BCE=90°+60°=150° (3)猜想∠ACB+∠DCE=180°,理由:因为∠ACB=∠ACE+∠ECB,∠ACD=∠ACE+∠DCE,所以∠ACB+∠DCE=∠ACE+∠ECB+∠ACD-∠ACE=∠ECB+∠ACD=90°+90°=180°
23.(11分)探索新知:
如图①,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线________这个角的“巧分线”;(填“是”或“不是”)
(2)如图②,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=________;(用含α的代数式表示)
深入研究:
(3)如图②,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请求出当射线PQ是∠MPN的“巧分线”时t的值.
解:(1)是 (2)α或α或α (3)依题意有:①10t=(5t+60),解得t=2.4;②10t=(5t+60),解得t=4;③10t=(5t+60),解得t=6.故当t为2.4或4或6时,射线PQ是∠MPN的“巧分线”
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列能用∠C表示∠1的是( )
2.下列几何体中,其侧面展开图为扇形的是( )
3.平面上4个点最多可以确定直线的条数为( )
A.4条 B.6条 C.8条 D.10条
4.一个角的余角的3倍比这个角的4倍大18°,则这个角等于( )
A.36° B.40° C.50° D.54°
5.数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( )
A.3 B.4.5 C.6 D.18
6.如图,已知∠1=∠2,∠3=∠4,有下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AE平分∠BAC,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第7题图)) eq \o(\s\up7(),\s\do5(第8题图))
7.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
8.如图,在时刻8:30,时钟上的时针和分针之间的夹角为( )
A.85° B.75° C.70° D.60°
9.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( )
A.传 B.因 C.承 D.基
eq \o(\s\up7(),\s\do5(第9题图)) eq \o(\s\up7(),\s\do5(第11题图))
10.在直线上顺次取A,B,C,D四点,并且使AB∶BC∶CD=2∶3∶4,如果AB中点M与CD中点N的距离是12 cm,那么CD的长是( )
A.4 cm B.6 cm C.8 cm D.24 cm
二、填空题(每小题3分,共15分)
11.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为____.
12.如图,数轴上A,B两点所表示的数分别是-4和2,点C是线段AB的中点,则点C所表示的数是__ _.
13.计算:(1)53°19′42″+16°40′18″=__ __;
(2)23°15′16″×5=__ __.
14.如图是由一副三角板拼成的两个图形,则:
(1)在第一个图形中,∠ACD=__ __,∠ABD=__ _;
(2)在第二个图形中,∠BAG=__ __,∠AGC=__ __.
15.已知A,B,C三点都在数轴上,点A在数轴上对应的数为2,且AB=5,BC=3,则点C在数轴上对应的数为__ __.
三、解答题(共75分)
16.(8分)如图是由七块相同的小正方体搭成的立体图形,请画出这个图形分别从正面看、从左面看和从上面看得到的平面图形.
17.(9分)已知∠1与∠2互为补角,∠2的度数的一半比∠1大45°,求∠1与∠2的度数.
18.(9分)画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个点?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
19.(9分)如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=AB,点E是AC的中点,点D是AB的中点,求DE的长.
20.(9分)如图,点M在线段AB上,线段BM与AM的长度之比为5∶4,点N为线段AM的中点.
(1)若AB=27 cm,求BN的长.
(2)在线段AB上作出一点E,满足MB=3EB,若ME=t,求AB的长(用含t的代数式表示).
21.(10分)如图,点A,O,B在同一条直线上,∠COB与∠BOD互余,OE,OF分别是∠AOC,∠AOD的平分线,求∠EOF的度数.
22.(10分)如图,将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由.
23.(11分)探索新知:
如图①,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线________这个角的“巧分线”;(填“是”或“不是”)
(2)如图②,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=________;(用含α的代数式表示)
深入研究:
(3)如图②,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请求出当射线PQ是∠MPN的“巧分线”时t的值.
答案:
第4章检测题(教师版)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列能用∠C表示∠1的是( C )
2.下列几何体中,其侧面展开图为扇形的是( C )
3.平面上4个点最多可以确定直线的条数为( B )
A.4条 B.6条 C.8条 D.10条
4.一个角的余角的3倍比这个角的4倍大18°,则这个角等于( A )
A.36° B.40° C.50° D.54°
5.数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( C )
A.3 B.4.5 C.6 D.18
6.如图,已知∠1=∠2,∠3=∠4,有下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AE平分∠BAC,其中正确的个数是( B )
A.1个 B.2个 C.3个 D.4个
eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第7题图)) eq \o(\s\up7(),\s\do5(第8题图))
7.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( D )
A.25° B.35° C.45° D.55°
8.如图,在时刻8:30,时钟上的时针和分针之间的夹角为( B )
A.85° B.75° C.70° D.60°
9.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( D )
A.传 B.因 C.承 D.基
eq \o(\s\up7(),\s\do5(第9题图)) eq \o(\s\up7(),\s\do5(第11题图))
10.在直线上顺次取A,B,C,D四点,并且使AB∶BC∶CD=2∶3∶4,如果AB中点M与CD中点N的距离是12 cm,那么CD的长是( C )
A.4 cm B.6 cm C.8 cm D.24 cm
二、填空题(每小题3分,共15分)
11.如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为__150°42′__.
12.如图,数轴上A,B两点所表示的数分别是-4和2,点C是线段AB的中点,则点C所表示的数是__-1__.
13.计算:(1)53°19′42″+16°40′18″=__70°__;
(2)23°15′16″×5=__116°16′20″__.
14.如图是由一副三角板拼成的两个图形,则:
(1)在第一个图形中,∠ACD=__75°__,∠ABD=__135°__;
(2)在第二个图形中,∠BAG=__45°__,∠AGC=__105°__.
15.已知A,B,C三点都在数轴上,点A在数轴上对应的数为2,且AB=5,BC=3,则点C在数轴上对应的数为__-6或0或4或10__.
三、解答题(共75分)
16.(8分)如图是由七块相同的小正方体搭成的立体图形,请画出这个图形分别从正面看、从左面看和从上面看得到的平面图形.
解:
17.(9分)已知∠1与∠2互为补角,∠2的度数的一半比∠1大45°,求∠1与∠2的度数.
解:∠1=30°,∠2=150°
18.(9分)画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个点?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
解:(1)如图:
(2)线段DC的中点是点A,AB=CD (3)因为BC=AB=×2=1 (cm),所以AC=AB+BC=2+1=3 (cm).又因为AD=AC=3 cm,所以BD=DA+AB=3+2=5 (cm)
19.(9分)如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=AB,点E是AC的中点,点D是AB的中点,求DE的长.
解:因为AB=24 cm,BC=AB=
×24=9(cm),所以AC=33 cm,又因为E是AC的中点,则AE=AC=16.5 cm,又因为D是AB的中点,则AD=AB=12 cm,所以DE=AE-AD=16.5-12=4.5(cm)
20.(9分)如图,点M在线段AB上,线段BM与AM的长度之比为5∶4,点N为线段AM的中点.
(1)若AB=27 cm,求BN的长.
(2)在线段AB上作出一点E,满足MB=3EB,若ME=t,求AB的长(用含t的代数式表示).
解:(1)由题知BM∶AM=5∶4,设BM=5x cm,AM=4x cm,∴AB=BM+AM=9x cm,∵AB=27 cm,∴9x=27,∴x=3.∴AM=12 cm,BM=15 cm.∵点N是线段AM的中点,∴MN=AM=6 cm,∴BN=BM+MN=15+6=21(cm) (2)∵BM∶AM=5∶4,∴AM=BM,∵BM=3EB,∴ME=BM=t,∴BM=t,∵AB=AM+BM=BM+BM=BM,∴AB=×t=t
21.(10分)如图,点A,O,B在同一条直线上,∠COB与∠BOD互余,OE,OF分别是∠AOC,∠AOD的平分线,求∠EOF的度数.
解:由∠COB与∠BOD互余得∠COD=90°,所以∠AOC+∠AOD=360°-90°=270°,又因为OE,OF分别是∠AOC,∠AOD的平分线,所以∠EOF=(∠AOC+∠AOD)=×270°=135°
22.(10分)如图,将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由.
解:(1)∠ACE=∠BCD,理由略 (2)因为∠DCE=30°,∠ACD=90°,∴∠ACE=∠ACD-∠DCE=90°-30°=60°,所以∠ACB=∠ACE+∠BCE=90°+60°=150° (3)猜想∠ACB+∠DCE=180°,理由:因为∠ACB=∠ACE+∠ECB,∠ACD=∠ACE+∠DCE,所以∠ACB+∠DCE=∠ACE+∠ECB+∠ACD-∠ACE=∠ECB+∠ACD=90°+90°=180°
23.(11分)探索新知:
如图①,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线________这个角的“巧分线”;(填“是”或“不是”)
(2)如图②,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=________;(用含α的代数式表示)
深入研究:
(3)如图②,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请求出当射线PQ是∠MPN的“巧分线”时t的值.
解:(1)是 (2)α或α或α (3)依题意有:①10t=(5t+60),解得t=2.4;②10t=(5t+60),解得t=4;③10t=(5t+60),解得t=6.故当t为2.4或4或6时,射线PQ是∠MPN的“巧分线”
