相似三角形判定复习
图片预览






文档简介
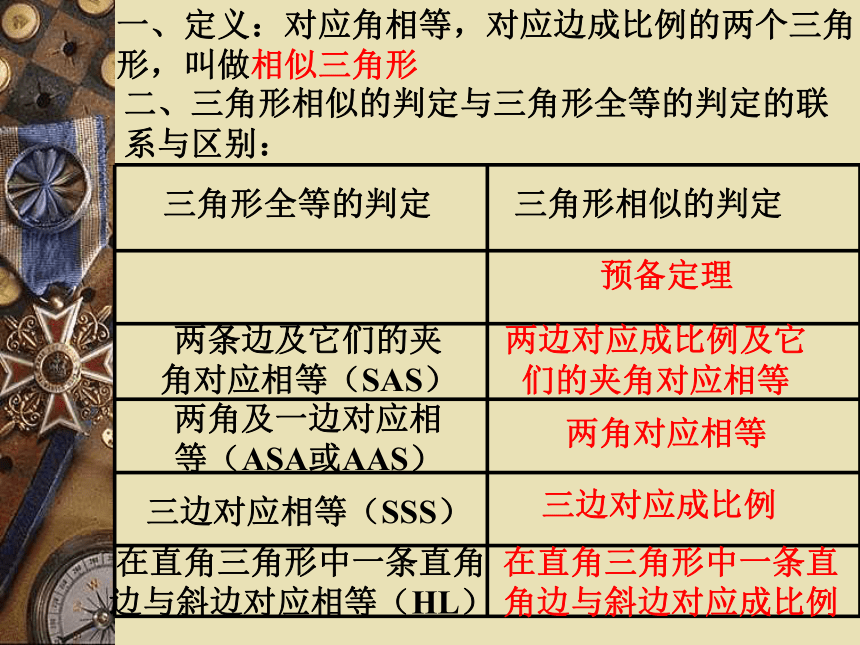
课件20张PPT。如何判定三角形相似一、定义:对应角相等,对应边成比例的两个三角形,叫做相似三角形二、三角形相似的判定与三角形全等的判定的联系与区别: 三角形全等的判定三角形相似的判定预备定理两条边及它们的夹角对应相等(SAS)两边对应成比例及它们的夹角对应相等两角及一边对应相等(ASA或AAS)两角对应相等三边对应相等(SSS)三边对应成比例在直角三角形中一条直角边与斜边对应相等(HL)在直角三角形中一条直角边与斜边对应成比例判定三角形相似的思路三、判定三角形相似的一般思维程序 1.有平行截线用预备定理2.有一组对角相等,找⑴另一组对角相等⑵夹这角的两边成比例3.有两边对应成比例,找⑴夹角相等⑵第三边成比例⑶有一对直角4.直角三角形 ,找⑴一对锐角相等⑵两条直角边对应成比例⑶斜边、直角边对应成比例5.等腰三角形,找 ⑴顶角相等
⑶底和腰成比例⑵一对底角相等四、过关训练1、下列判断中,正确的有
(A)有两边对应成比例,且有一个角对应相等 的两个三角形相似;
(B)有一个锐角相等的两个等腰三角形相似;
(C)有一个锐角对应相等的两个直角三角形相似;
(D)任意两个等腰直角三角形都相似。(C) (D)2、如果一个三角形的一条高分这个三角形为两个相似三角形,那么这个三角形是
(A)等腰三角形 (B)任意三角形
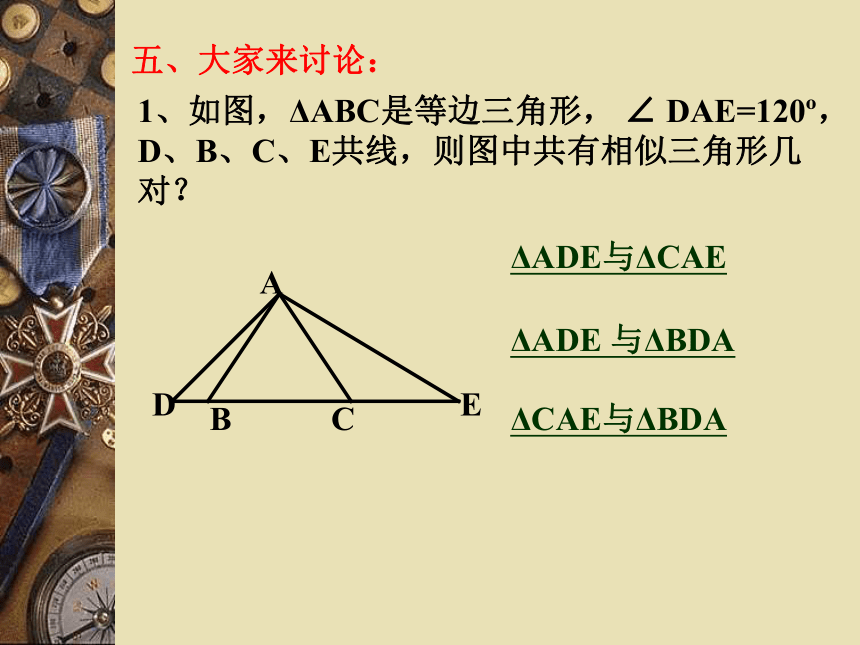
(C)直角三角形 (D)直角三角形或等腰三角形(D)五、大家来讨论:
1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?
ΔADE与ΔCAE
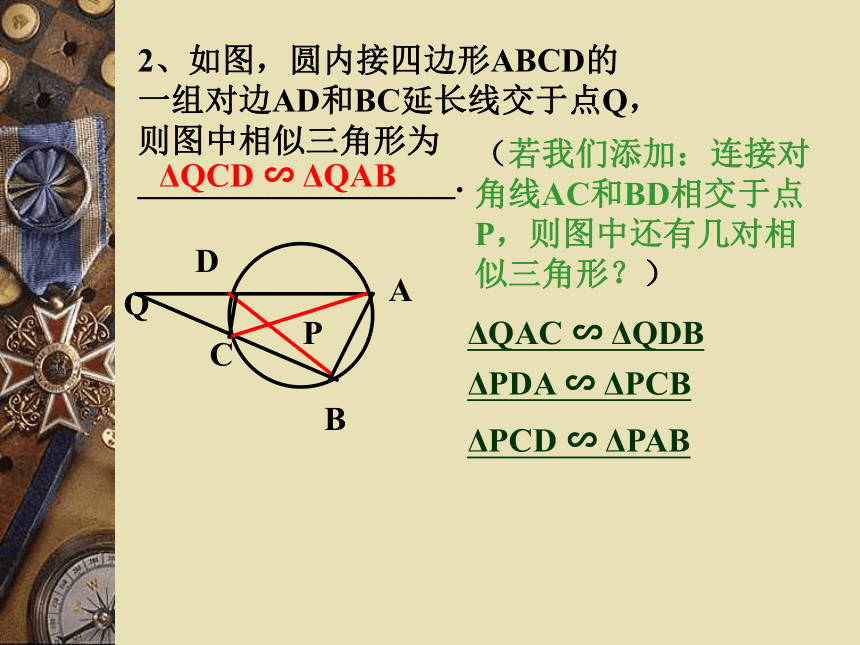
ΔADE 与ΔBDAΔCAE与ΔBDA2、如图,圆内接四边形ABCD的一组对边AD和BC延长线交于点Q,则图中相似三角形为___________________.DQBCAΔQCD ∽ ΔQAB(若我们添加:连接对角线AC和BD相交于点P,则图中还有几对相似三角形?) ΔQAC ∽ ΔQDBΔPDA ∽ ΔPCB
ΔPCD ∽ ΔPAB
六、小结: 由三角形全等的研究到三角形相似的研究,实质上是对几何中保距变换的研究进入保角变换的研究,全等三角形与相似三角形的共性是角的关系仍然保持对应相等(即保角变换),而对应边的关系,则由相等飞跃到只需对应成比例(非保距变换),在这一点上相似三角形比全等三角形的条件削弱了,因此判定上相应地可比全等三角形的判定条件减少了,但注意这里只削弱了边的相等关系,因此研究相似三角形比研究全等三角形更具有一般性,体现在方法上也就更加灵活多变了。作业:书 P149、6、7 、 P160、21、 P162、29、(选做)谢谢大家,再见! 问题:(如图)已知DE∥AB.若要证△CED∽△CAB,需用什么定理?
ABCED问题:(如图)已知∠D=∠B,若要证△ABC∽△ADE,还需要找什么条件?① 找 ∠DAE=∠BACDOBECA
问题:(如图)已知若要证△ABC∽△ADB,还需找什么条件?
ABCD①找 ∠BAC=∠DAB③找 ∠ABC=∠ADB=RT∠问题:(如图)在RT △ ABC中,∠C=RT∠,DE⊥AB,若要证△ADE∽△ABC,还需找什么条件?ABCE①找∠DAE=∠BAC或∠ABC=∠ADED问题:(如图)已知△ABC与△DEF都是等腰三角形。若要证△ABC∽△DEF,还需找什么条件?ACBDFE①找∠A=∠D②找∠B=∠E或∠C=∠FA1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?
证明:在等边三角形ΔABC中
∠ACB= ∠ ABC =∠ BAC∠ACE= 120o
∠ DAE=120o∠ACE= ∠ DAE∠ AED= ∠ CEAΔ ADE ∽ ΔCAE1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?
证明:在等边三角形ΔABC中
∠ACB= ∠ ABC =∠ BAC∠ABD= 120o
∠ DAE=120o
∠ABD= ∠ DAE∠ ADE= ∠ BDAΔ ADE ∽ ΔBDA
DABCE1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?证明:在等边三角形ΔABC中
∠ACB= ∠ ABC =∠ BAC
∠ACE= ∠ BDA= 120o
∠ DAE=120o∠DAB+∠ EAC=60o∠DAB+∠ ADB=60o
∠ADB=∠ EACΔ CAE∽ Δ BDADBCAQΔQAC ∽ ΔQDB
证明:∠AQC= ∠ BQD ∠QAC= ∠ QBD
DQBCAP证明:∠ADB= ∠ BCA ∠DAC= ∠ CBDΔPDA∽ ΔPCB
DQBCAP证明:∠CDB= ∠CAB ∠DCA= ∠ABDΔPCD∽ ΔPAB
⑶底和腰成比例⑵一对底角相等四、过关训练1、下列判断中,正确的有
(A)有两边对应成比例,且有一个角对应相等 的两个三角形相似;
(B)有一个锐角相等的两个等腰三角形相似;
(C)有一个锐角对应相等的两个直角三角形相似;
(D)任意两个等腰直角三角形都相似。(C) (D)2、如果一个三角形的一条高分这个三角形为两个相似三角形,那么这个三角形是
(A)等腰三角形 (B)任意三角形
(C)直角三角形 (D)直角三角形或等腰三角形(D)五、大家来讨论:
1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?
ΔADE与ΔCAE
ΔADE 与ΔBDAΔCAE与ΔBDA2、如图,圆内接四边形ABCD的一组对边AD和BC延长线交于点Q,则图中相似三角形为___________________.DQBCAΔQCD ∽ ΔQAB(若我们添加:连接对角线AC和BD相交于点P,则图中还有几对相似三角形?) ΔQAC ∽ ΔQDBΔPDA ∽ ΔPCB
ΔPCD ∽ ΔPAB
六、小结: 由三角形全等的研究到三角形相似的研究,实质上是对几何中保距变换的研究进入保角变换的研究,全等三角形与相似三角形的共性是角的关系仍然保持对应相等(即保角变换),而对应边的关系,则由相等飞跃到只需对应成比例(非保距变换),在这一点上相似三角形比全等三角形的条件削弱了,因此判定上相应地可比全等三角形的判定条件减少了,但注意这里只削弱了边的相等关系,因此研究相似三角形比研究全等三角形更具有一般性,体现在方法上也就更加灵活多变了。作业:书 P149、6、7 、 P160、21、 P162、29、(选做)谢谢大家,再见! 问题:(如图)已知DE∥AB.若要证△CED∽△CAB,需用什么定理?
ABCED问题:(如图)已知∠D=∠B,若要证△ABC∽△ADE,还需要找什么条件?① 找 ∠DAE=∠BACDOBECA
问题:(如图)已知若要证△ABC∽△ADB,还需找什么条件?
ABCD①找 ∠BAC=∠DAB③找 ∠ABC=∠ADB=RT∠问题:(如图)在RT △ ABC中,∠C=RT∠,DE⊥AB,若要证△ADE∽△ABC,还需找什么条件?ABCE①找∠DAE=∠BAC或∠ABC=∠ADED问题:(如图)已知△ABC与△DEF都是等腰三角形。若要证△ABC∽△DEF,还需找什么条件?ACBDFE①找∠A=∠D②找∠B=∠E或∠C=∠FA1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?
证明:在等边三角形ΔABC中
∠ACB= ∠ ABC =∠ BAC∠ACE= 120o
∠ DAE=120o∠ACE= ∠ DAE∠ AED= ∠ CEAΔ ADE ∽ ΔCAE1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?
证明:在等边三角形ΔABC中
∠ACB= ∠ ABC =∠ BAC∠ABD= 120o
∠ DAE=120o
∠ABD= ∠ DAE∠ ADE= ∠ BDAΔ ADE ∽ ΔBDA
DABCE1、如图,ΔABC是等边三角形, ∠ DAE=120o,D、B、C、E共线,则图中共有相似三角形几对?证明:在等边三角形ΔABC中
∠ACB= ∠ ABC =∠ BAC
∠ACE= ∠ BDA= 120o
∠ DAE=120o∠DAB+∠ EAC=60o∠DAB+∠ ADB=60o
∠ADB=∠ EACΔ CAE∽ Δ BDADBCAQΔQAC ∽ ΔQDB
证明:∠AQC= ∠ BQD ∠QAC= ∠ QBD
DQBCAP证明:∠ADB= ∠ BCA ∠DAC= ∠ CBDΔPDA∽ ΔPCB
DQBCAP证明:∠CDB= ∠CAB ∠DCA= ∠ABDΔPCD∽ ΔPAB
