新人教版6年级上册 3.8 解决问题(4)课件(30张PPT)
文档属性
| 名称 | 新人教版6年级上册 3.8 解决问题(4)课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-30 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
3.7 解决问题(4)
第三单元 分数除法
新人教版六年级上册
教学目标
1.使学生理解“工程问题”的特点、数量关系:掌握解题方法,并能正确解答。
2.通过解答“工程问题”,培养学生的比较、分析能力和逻辑思维能力。
3.在解决问题的过程中,体会数学与生活的密切联系,感受学习分数除法的价值,培养学习数学的兴趣,树立学好数学的信心
1.修一条360米的公路,甲队修12天完成,平均每天( )米。
2.修一条360米的公路,甲队每天修18米,( )天能完成。
填一填。
30
20
以上问题涉及到了哪个知识点?那它们的关系又如何呢?
工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
课前导入
探究点1 掌握用假设、验证等方法解决问题的基本策略,体会模型思想
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天才能修完。
问题:
如果两队合修,多少天能修完?
探索新知
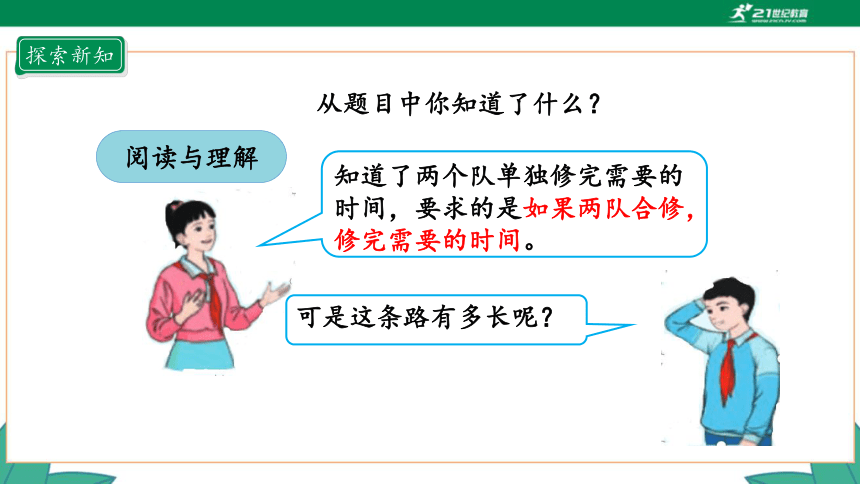
阅读与理解
从题目中你知道了什么?
知道了两个队单独修完需要的时间,要求的是如果两队合修,修完需要的时间。
可是这条路有多长呢?
探索新知
分析与解答
可以假设这条道路长18千米。
18千米
18÷18=1(千米)
工作总量÷工作时间=工作效率
工作总量÷效率和=工作时间
两队的效率和
方法1:假设道路全长为18km
探索新知
分析与解答
我假设这条道路长30千米。
30千米
方法2:假设道路全长为30km
探索新知
思考:
① 我们假设这条路的长度都不同,但最终的结果是相同的,那么这条路的长度还可以看做是多少千米?
② 这条路的长度可以看做是“1”吗?
③ 如果把这条路的长度看做是“1”,应该怎样解答?
探索新知
分析与解答
也可以假设这条道路的长度是“1”。
1
方法3:假设道路全长为1
探索新知
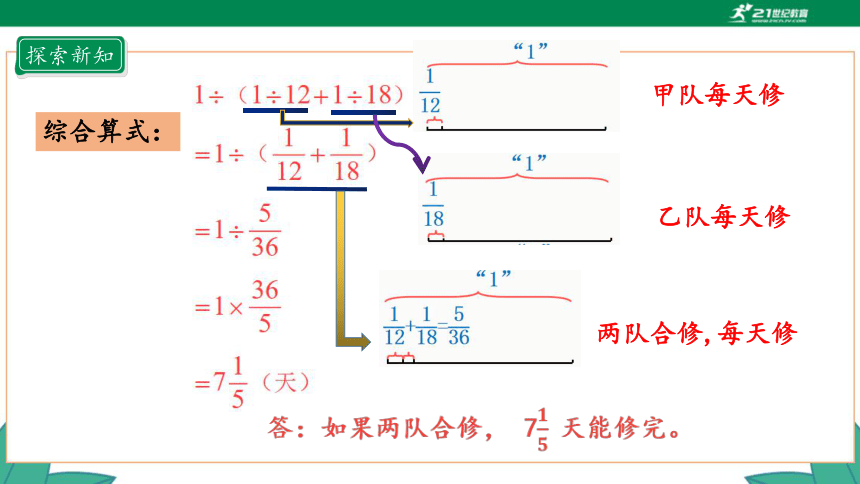
综合算式:
甲队每天修
乙队每天修
两队合修,每天修
答:如果两队合修, 7天能修完。
探索新知
①假设全长为18km
②假设全长为30km
③假设全长为“1”
要点提示
不管假设这条路有多长,答案都是相同的。把道路长假设成1,解答要简便。
探索新知
把道路假设成不同的长度,得出了相同的结果,这个结果对吗?可以怎样检验?
回顾与反思
说明计算正确。
探索新知
归纳总结:
(1)用分数解决工程问题的解题方法与用整数解决工程问题的解题方法相同,所用的数量关系也相同。
工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
(2)用分数解决工程问题时,把工作总量看作单位“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
探索新知
一批货物,只用甲车运,6 次能运完;只用乙车运,3 次能运完。如果两辆车一起运,多少次能运完这批货物?
答:两辆车一起运,2次能运完这批货物。
把这批货物看作“1”
【课本P41 做一做】
课堂练习
1. 挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天能挖整条水渠的 。两人合作,几天能挖完?
答:两人合作,12天能挖完。
“1”
【课本P42 练习九第6题】
课堂练习
2.修一条公路,甲队单独修要4天完成,乙队单独修要6天完成。两队合修几天完成?
答:两队合修 天完成。
“1”
课堂练习
3. 甲车从 A 城市到 B 城市要行驶 2 小时,乙车从 B
城市到 A 城市要行驶 3 小时。两车同时分别从 A
城市和 B 城市出发,相向而行,几小时后相遇?
答: 小时后相遇。
【课本P42 练习九 第7题】
课堂练习
4. 某水库准备打开泄洪口调节水位。只打开 A 口,
8小时可以完成任务;只打开 B 口,6 小时可以
完成任务。如果两个泄洪口同时打开,几小时
可以完成任务?
答: 小时可以完成任务。
【课本P43 练习九 第8题】
人教版数学六年级上册精编版教学PPT课件
课堂练习
5. 植树队要种 300 棵树。甲队单独种,种完需要
8天;乙队单独种,种完需要 10 天。现在两队
合种,5 天能种完吗?
答:现在两队合种,5天能种完。
【课本P43 练习九 第9题】
易错点:当工作总量用具体量计算时,要注意工作效率也要用具体量表示。如:用300计算时,一队的工作效率是 300÷8。
人教版数学六年级上册精编版教学PPT课件
课堂练习
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
说一说,怎样解决这类工程问题?
把工作总量看作“1” ——工作总量÷效率和=合作时间
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
【课本P40 例7】
假设这条道路是1。
课堂小结
3.7 解决问题(4)
第三单元 分数除法
新人教版六年级上册
教学目标
1.使学生理解“工程问题”的特点、数量关系:掌握解题方法,并能正确解答。
2.通过解答“工程问题”,培养学生的比较、分析能力和逻辑思维能力。
3.在解决问题的过程中,体会数学与生活的密切联系,感受学习分数除法的价值,培养学习数学的兴趣,树立学好数学的信心
1.修一条360米的公路,甲队修12天完成,平均每天( )米。
2.修一条360米的公路,甲队每天修18米,( )天能完成。
填一填。
30
20
以上问题涉及到了哪个知识点?那它们的关系又如何呢?
工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
课前导入
探究点1 掌握用假设、验证等方法解决问题的基本策略,体会模型思想
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天才能修完。
问题:
如果两队合修,多少天能修完?
探索新知
阅读与理解
从题目中你知道了什么?
知道了两个队单独修完需要的时间,要求的是如果两队合修,修完需要的时间。
可是这条路有多长呢?
探索新知
分析与解答
可以假设这条道路长18千米。
18千米
18÷18=1(千米)
工作总量÷工作时间=工作效率
工作总量÷效率和=工作时间
两队的效率和
方法1:假设道路全长为18km
探索新知
分析与解答
我假设这条道路长30千米。
30千米
方法2:假设道路全长为30km
探索新知
思考:
① 我们假设这条路的长度都不同,但最终的结果是相同的,那么这条路的长度还可以看做是多少千米?
② 这条路的长度可以看做是“1”吗?
③ 如果把这条路的长度看做是“1”,应该怎样解答?
探索新知
分析与解答
也可以假设这条道路的长度是“1”。
1
方法3:假设道路全长为1
探索新知
综合算式:
甲队每天修
乙队每天修
两队合修,每天修
答:如果两队合修, 7天能修完。
探索新知
①假设全长为18km
②假设全长为30km
③假设全长为“1”
要点提示
不管假设这条路有多长,答案都是相同的。把道路长假设成1,解答要简便。
探索新知
把道路假设成不同的长度,得出了相同的结果,这个结果对吗?可以怎样检验?
回顾与反思
说明计算正确。
探索新知
归纳总结:
(1)用分数解决工程问题的解题方法与用整数解决工程问题的解题方法相同,所用的数量关系也相同。
工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
(2)用分数解决工程问题时,把工作总量看作单位“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
探索新知
一批货物,只用甲车运,6 次能运完;只用乙车运,3 次能运完。如果两辆车一起运,多少次能运完这批货物?
答:两辆车一起运,2次能运完这批货物。
把这批货物看作“1”
【课本P41 做一做】
课堂练习
1. 挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天能挖整条水渠的 。两人合作,几天能挖完?
答:两人合作,12天能挖完。
“1”
【课本P42 练习九第6题】
课堂练习
2.修一条公路,甲队单独修要4天完成,乙队单独修要6天完成。两队合修几天完成?
答:两队合修 天完成。
“1”
课堂练习
3. 甲车从 A 城市到 B 城市要行驶 2 小时,乙车从 B
城市到 A 城市要行驶 3 小时。两车同时分别从 A
城市和 B 城市出发,相向而行,几小时后相遇?
答: 小时后相遇。
【课本P42 练习九 第7题】
课堂练习
4. 某水库准备打开泄洪口调节水位。只打开 A 口,
8小时可以完成任务;只打开 B 口,6 小时可以
完成任务。如果两个泄洪口同时打开,几小时
可以完成任务?
答: 小时可以完成任务。
【课本P43 练习九 第8题】
人教版数学六年级上册精编版教学PPT课件
课堂练习
5. 植树队要种 300 棵树。甲队单独种,种完需要
8天;乙队单独种,种完需要 10 天。现在两队
合种,5 天能种完吗?
答:现在两队合种,5天能种完。
【课本P43 练习九 第9题】
易错点:当工作总量用具体量计算时,要注意工作效率也要用具体量表示。如:用300计算时,一队的工作效率是 300÷8。
人教版数学六年级上册精编版教学PPT课件
课堂练习
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
巩固提升
说一说,怎样解决这类工程问题?
把工作总量看作“1” ——工作总量÷效率和=合作时间
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
【课本P40 例7】
假设这条道路是1。
课堂小结
