24.4弧长及扇形的面积课件
文档属性
| 名称 | 24.4弧长及扇形的面积课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-15 00:00:00 | ||
图片预览






文档简介
课件22张PPT。弧长及扇形的面积 .1、圆周长公式:
2、圆面积公式:
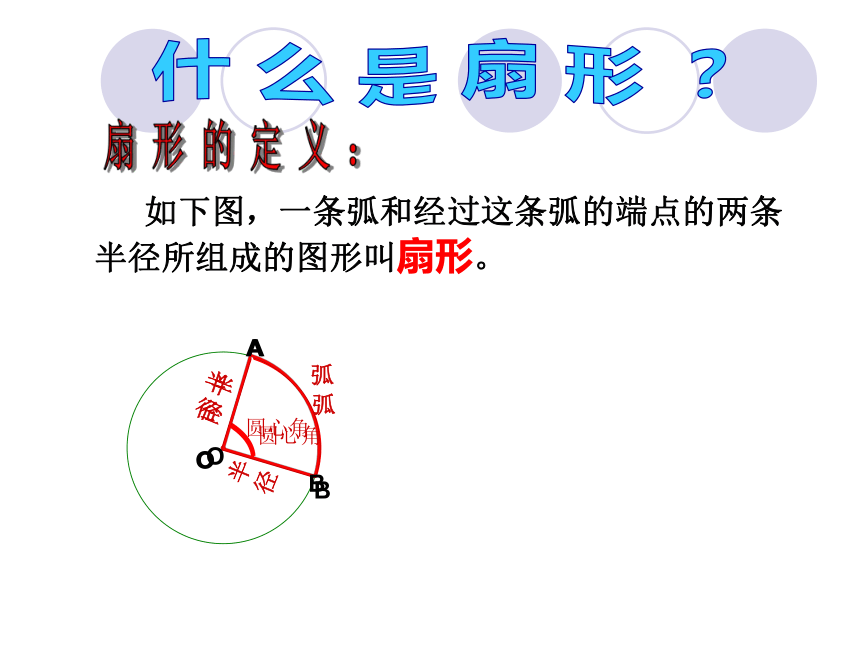
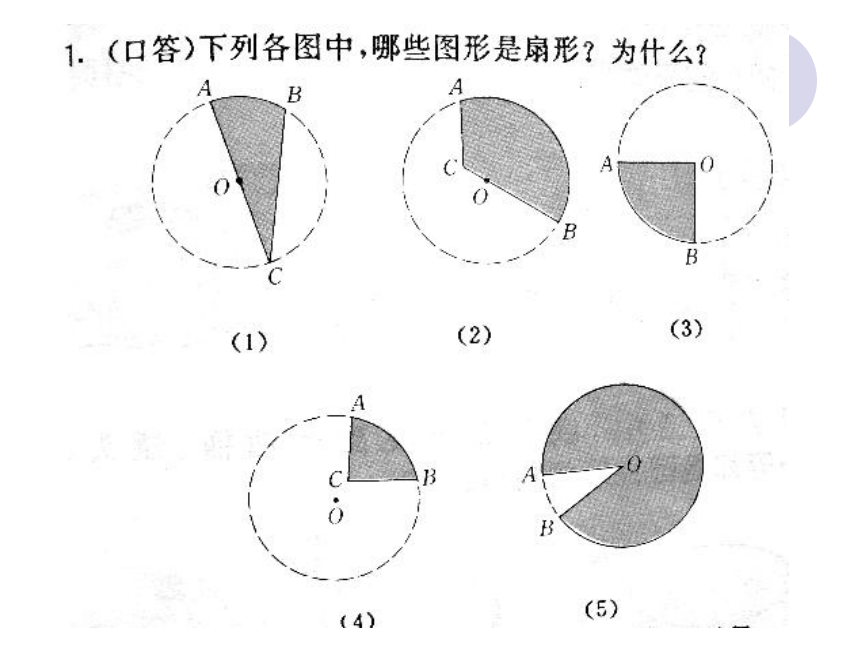
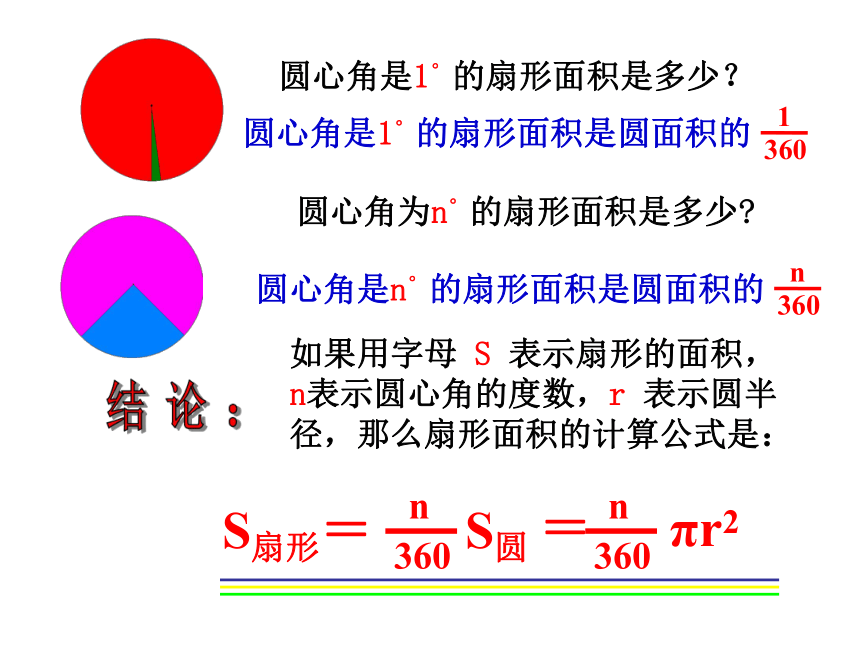
温故知新问题1.已知⊙O半径为R,求n°圆心角所对弧长 .弧长公式 即若设⊙O半径为R, n°的圆心角所对的弧长为 ,则 问题探究什 么 是 扇 形 ? 如下图,一条弧和经过这条弧的端点的两条半径所组成的图形叫扇形。扇 形 的 定 义 :圆心角圆心角是1°的扇形面积是多少?圆心角为n°的扇形面积是多少?结 论 :如果用字母 S 表示扇形的面积,n表示圆心角的度数,r 表示圆半径,那么扇形面积的计算公式是:小试牛刀填空题(4)已知扇形面积为5π,圆心角为50°,则这个扇形的半径R=____. 6思考:扇形的面积公式与弧长公式有联系吗? 如果扇形的半径为R,弧长为l ,那么扇形面积的计算公式又该怎样表示?扇形的弧长与扇形面积的关系为:思考扇形的面积公式和以前学过的什么公式形式上一样?试一试3、一扇形的弧长是 ,面积为
那么扇形的圆心角为 . 150度2、已知扇形面积为3π,圆心角为30°,则这个扇形的半径r=____. 6变式题:若扇形的圆心角为150°,弧长为 ,则这个扇形的面积为____ . 1、已知半径为2cm的扇形,其弧长为 cm,
则这个扇形的面积,S扇= .1. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.C为切点,设AB的长为d,圆环面积为S,则S与d之间有怎样的数量关系?探究题.解:2. 如图,正三角形ABC的边长为a,分别以A、B、C为圆心, 为半径的圆两两相切于点O1、O2、O3,求弧O1O2、弧O2O3、弧O3O1围成的图形的面积S(图中阴影部分).1、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是
2、扇形的面积是S,它的半径是r,这个扇形的弧长是240°中考链接3、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。4.扇形所在圆的圆心角度数为150°,
L=20πcm,
求:(1).扇形所在圆的半径;
(2).扇形的面积;
5.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为BB6、如图,在Rt△ABC中,∠C=900,AC=2,
AB=4,分别以AC,BC为直径作圆,则
图中阴影部分面积为如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?学以致用1.如图、水平放置的圆柱形排水管道的截面半径是1.6cm,其中水面高0.8cm,求截面上有水部分的面积。(精确到0.01cm)。CDS阴影= S扇- S⊿OAB延伸拓展变式题: 如图、水平放置的圆柱形排水管道的截面半径是1.6cm,其中水面高1.2cm,求截面上有水部分的面积。(精确到0.01cm)。ABDCES阴影 = S扇+ S⊿OAB1.本节课你有哪些收获?小结2.你了解了哪些数学思想方法?总结1、弧长的计算公式2、扇形面积计算公式3、不规则图形的面积的求法:
用规则的图形的面积来表示; 4、数学思想转化的应用:
①转化思想;②整体思想。谢谢各位!
2、圆面积公式:
温故知新问题1.已知⊙O半径为R,求n°圆心角所对弧长 .弧长公式 即若设⊙O半径为R, n°的圆心角所对的弧长为 ,则 问题探究什 么 是 扇 形 ? 如下图,一条弧和经过这条弧的端点的两条半径所组成的图形叫扇形。扇 形 的 定 义 :圆心角圆心角是1°的扇形面积是多少?圆心角为n°的扇形面积是多少?结 论 :如果用字母 S 表示扇形的面积,n表示圆心角的度数,r 表示圆半径,那么扇形面积的计算公式是:小试牛刀填空题(4)已知扇形面积为5π,圆心角为50°,则这个扇形的半径R=____. 6思考:扇形的面积公式与弧长公式有联系吗? 如果扇形的半径为R,弧长为l ,那么扇形面积的计算公式又该怎样表示?扇形的弧长与扇形面积的关系为:思考扇形的面积公式和以前学过的什么公式形式上一样?试一试3、一扇形的弧长是 ,面积为
那么扇形的圆心角为 . 150度2、已知扇形面积为3π,圆心角为30°,则这个扇形的半径r=____. 6变式题:若扇形的圆心角为150°,弧长为 ,则这个扇形的面积为____ . 1、已知半径为2cm的扇形,其弧长为 cm,
则这个扇形的面积,S扇= .1. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.C为切点,设AB的长为d,圆环面积为S,则S与d之间有怎样的数量关系?探究题.解:2. 如图,正三角形ABC的边长为a,分别以A、B、C为圆心, 为半径的圆两两相切于点O1、O2、O3,求弧O1O2、弧O2O3、弧O3O1围成的图形的面积S(图中阴影部分).1、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是
2、扇形的面积是S,它的半径是r,这个扇形的弧长是240°中考链接3、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。4.扇形所在圆的圆心角度数为150°,
L=20πcm,
求:(1).扇形所在圆的半径;
(2).扇形的面积;
5.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为BB6、如图,在Rt△ABC中,∠C=900,AC=2,
AB=4,分别以AC,BC为直径作圆,则
图中阴影部分面积为如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?学以致用1.如图、水平放置的圆柱形排水管道的截面半径是1.6cm,其中水面高0.8cm,求截面上有水部分的面积。(精确到0.01cm)。CDS阴影= S扇- S⊿OAB延伸拓展变式题: 如图、水平放置的圆柱形排水管道的截面半径是1.6cm,其中水面高1.2cm,求截面上有水部分的面积。(精确到0.01cm)。ABDCES阴影 = S扇+ S⊿OAB1.本节课你有哪些收获?小结2.你了解了哪些数学思想方法?总结1、弧长的计算公式2、扇形面积计算公式3、不规则图形的面积的求法:
用规则的图形的面积来表示; 4、数学思想转化的应用:
①转化思想;②整体思想。谢谢各位!
同课章节目录
