第六章 反比例函数 检测题(有答案)北师大版数学九年级上册
文档属性
| 名称 | 第六章 反比例函数 检测题(有答案)北师大版数学九年级上册 |  | |
| 格式 | DOC | ||
| 文件大小 | 700.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 17:56:11 | ||
图片预览



文档简介
第六章检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列函数中,变量y是x的反比例函数的是( )
A.y= B.y=5x-1 C.y= D.y=+1
2.已知反比例函数的图象经过点(2,-4),那么这个反比例函数的表达式是( )
A.y= B.y=- C.y= D.y=-
3.对于反比例函数y=-,下列说法错误的是( )
A.图象经过点(1,-5) B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小 D.当x>0时,y随x的增大而增大
4.若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
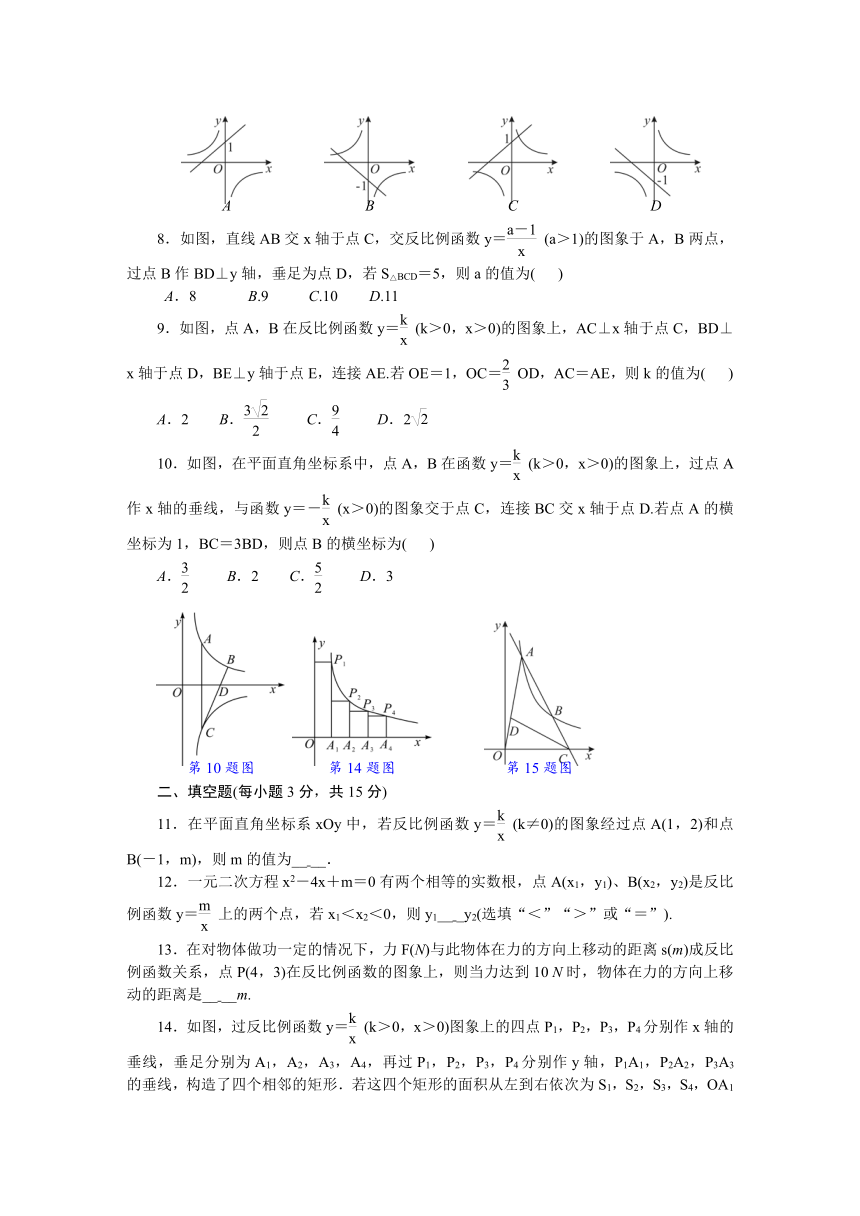
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数表达式为I= B.蓄电池的电压是18 V
C.当I≤10 A时,R≥3.6 Ω D.当R=6 Ω时,I=4 A
eq \o(\s\up7(),\s\do5(第5题图)) eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图))
6.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0,x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是( )
A.2<x<6 B.2≤x≤6 C.x>2 D.x<6
7.在同一平面直角坐标系中,函数y=kx+1与y=-(k为常数且k≠0)的图象大致是( )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A,B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
9.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,AC⊥x轴于点C,BD⊥x轴于点D,BE⊥y轴于点E,连接AE.若OE=1,OC=OD,AC=AE,则k的值为( )
A.2 B. C. D.2
10.如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图象上,过点A作x轴的垂线,与函数y=-(x>0)的图象交于点C,连接BC交x轴于点D.若点A的横坐标为1,BC=3BD,则点B的横坐标为( )
A. B.2 C. D.3
eq \o(\s\up7(),\s\do5(第10题图)) eq \o(\s\up7(),\s\do5(第14题图)) eq \o(\s\up7(),\s\do5(第15题图))
二、填空题(每小题3分,共15分)
11.在平面直角坐标系xOy中,若反比例函数y=(k≠0)的图象经过点A(1,2)和点B(-1,m),则m的值为__ __.
12.一元二次方程x2-4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1__ _y2(选填“<”“>”或“=”).
13.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,点P(4,3)在反比例函数的图象上,则当力达到10 N时,物体在力的方向上移动的距离是__ __m.
14.如图,过反比例函数y=(k>0,x>0)图象上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为 .
15.如图,反比例函数y=(k>0)在第一象限的图象上有A(1,6),B(3,b)两点,直线AB与x轴相交于点C,D是线段OA上一点.若AD·BC=AB·DO,连接CD,记△ADC,△DOC的面积分别为S1,S2,则S1-S2的值为__ __.
三、解答题(共75分)
16.(8分)已知y是x的反比例函数,并且当x=2时,y=6.
(1)求y关于x的函数表达式;
(2)当x=4时,求y的值.
17.(9分)已知反比例函数y=的图象分别位于第二、四象限,化简:-+.
18.(9分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式;
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
19.(9分)(2022·兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴,垂足为B(3,0),过C(5,0)作CD⊥x轴,交过点B的一次函数y=x+b的图象于点D,交反比例函数的图象于点E,S△AOB=3.
(1)求反比例比数和一次函数的表达式;
(2)求DE的长.
20.(9分)如图,一次函数y=kx+b的图象与x轴正半轴相交于点C,与反比例函数y=-的图象在第二象限相交于点A(-1,m),过点A作AD⊥x轴,垂足为D,且AD=CD.
(1)求一次函数的表达式;
(2)已知点E(a,0)满足CE=CA,求a的值.
21.(10分)如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC.
(1)求直线AB与双曲线的表达式;
(2)求△ABC的面积.
22.(10分)如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A(1,2),B(-2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出满足k1x+b>的x的取值范围;
(3)若点P在线段AB上,且S△AOP∶S△BOP=1∶4,求点P的坐标.
23.(11分)如图1,点A(0,8),点B(2,a)在直线y=-2x+b上,反比例函数y=(x>0)的图象经过点B.
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC,BD.
①如图2,当m=3时,过点D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;
②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三角形,求所有满足条件的m的值.
答案:
第六章检测题(教师版)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列函数中,变量y是x的反比例函数的是( B )
A.y= B.y=5x-1 C.y= D.y=+1
2.已知反比例函数的图象经过点(2,-4),那么这个反比例函数的表达式是( D )
A.y= B.y=- C.y= D.y=-
3.对于反比例函数y=-,下列说法错误的是( C )
A.图象经过点(1,-5) B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小 D.当x>0时,y随x的增大而增大
4.若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( B )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( C )
A.函数表达式为I= B.蓄电池的电压是18 V
C.当I≤10 A时,R≥3.6 Ω D.当R=6 Ω时,I=4 A
eq \o(\s\up7(),\s\do5(第5题图)) eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图))
6.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0,x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是( A )
A.2<x<6 B.2≤x≤6 C.x>2 D.x<6
7.在同一平面直角坐标系中,函数y=kx+1与y=-(k为常数且k≠0)的图象大致是( A )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A,B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( D )
A.8 B.9 C.10 D.11
9.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,AC⊥x轴于点C,BD⊥x轴于点D,BE⊥y轴于点E,连接AE.若OE=1,OC=OD,AC=AE,则k的值为( B )
A.2 B. C. D.2
10.如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图象上,过点A作x轴的垂线,与函数y=-(x>0)的图象交于点C,连接BC交x轴于点D.若点A的横坐标为1,BC=3BD,则点B的横坐标为( B )
A. B.2 C. D.3
eq \o(\s\up7(),\s\do5(第10题图)) eq \o(\s\up7(),\s\do5(第14题图)) eq \o(\s\up7(),\s\do5(第15题图))
二、填空题(每小题3分,共15分)
11.在平面直角坐标系xOy中,若反比例函数y=(k≠0)的图象经过点A(1,2)和点B(-1,m),则m的值为__-2__.
12.一元二次方程x2-4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1__>__y2(选填“<”“>”或“=”).
13.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,点P(4,3)在反比例函数的图象上,则当力达到10 N时,物体在力的方向上移动的距离是__1.2__m.
14.如图,过反比例函数y=(k>0,x>0)图象上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为__S1=4S4__.
15.如图,反比例函数y=(k>0)在第一象限的图象上有A(1,6),B(3,b)两点,直线AB与x轴相交于点C,D是线段OA上一点.若AD·BC=AB·DO,连接CD,记△ADC,△DOC的面积分别为S1,S2,则S1-S2的值为__4__.
三、解答题(共75分)
16.(8分)已知y是x的反比例函数,并且当x=2时,y=6.
(1)求y关于x的函数表达式;
(2)当x=4时,求y的值.
解:(1)由题意,设y=(k≠0),当x=2时,y=6.所以k=12,所以y= (2)当x=4时,y=3
17.(9分)已知反比例函数y=的图象分别位于第二、四象限,化简:-+.
解:∵反比例函数y=的图象分别位于第二、第四象限,∴k<0,∴k-1<0,∴原式=+=k+4+=k+4+|k-1|=k+4-k+1=5
18.(9分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式;
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
解:(1)v=
(2)∵要求不超过5小时卸完船上的这批货物,∴t≤5,则v≥=20,答:平均每小时至少要卸货20吨
19.(9分)(2022·兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴,垂足为B(3,0),过C(5,0)作CD⊥x轴,交过点B的一次函数y=x+b的图象于点D,交反比例函数的图象于点E,S△AOB=3.
(1)求反比例比数和一次函数的表达式;
(2)求DE的长.
解:(1)y=;y=x-
(2)∵过C(5,0)作CD⊥x轴,交过点B的一次函数y=x+b的图象于点D,∴当x=5时,y==,y=x-=3,∴E(5,),D(5,3),∴DE=3-=
20.(9分)如图,一次函数y=kx+b的图象与x轴正半轴相交于点C,与反比例函数y=-的图象在第二象限相交于点A(-1,m),过点A作AD⊥x轴,垂足为D,且AD=CD.
(1)求一次函数的表达式;
(2)已知点E(a,0)满足CE=CA,求a的值.
解:(1)∵点A(-1,m)在反比例函数y=-的图象上,∴-m=-2,解得m=2,∴A(-1,2),∵AD⊥x轴,∴AD=2,OD=1,∵CD=AD=2,∴OC=1,∴C(1,0).把点A(-1,2),C(1,0)代入y=kx+b中,得解得∴一次函数的表达式为y=-x+1
(2)在Rt△ADC中,AC==2,∴AC=CE=2,当点E在点C的左侧时,a=1-2,当点E在点C的右侧时,a=1+2,∴a的值为1±2
21.(10分)如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC.
(1)求直线AB与双曲线的表达式;
(2)求△ABC的面积.
解:(1)直线AB的表达式为y=2x+4,双曲线的表达式为y=
(2)过点B作BG∥x轴,过点C作FG∥y轴,FG和BG交于点G,过点B作BE∥y轴,过点A作FA∥x轴,BE和FA交于点E,设直线BO的表达式为y=ax,易知点B(-3,-2),∴-2=-3a,解得a=,∴直线BO的表达式为y=x,联立解得或∴点C的坐标为(3,2),∵点A(1,6),B(-3,-2),C(3,2),∴EB=8,BG=6,CG=4,CF=4,AF=2,AE=4,∴S△ABC=S矩形EBGF-S△AEB-S△BGC-S△AFC=8×6---=48-16-12-4=16
22.(10分)如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A(1,2),B(-2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出满足k1x+b>的x的取值范围;
(3)若点P在线段AB上,且S△AOP∶S△BOP=1∶4,求点P的坐标.
解:(1)∵反比例函数y=经过A(1,2),∴k2=1×2=2,∴反比例函数的表达式为y=,∵B(-2,n)在反比例函数y=的图象上,∴n==-1,∴B(-2,-1),∵直线y=k1x+b经过A(1,2),B(-2,-1),∴解得∴一次函数的表达式为y=x+1 (2)观察图象,k1x+b>的x的取值范围是-2<x<0或x>1 (3)设P(x,x+1),则-223.(11分)如图1,点A(0,8),点B(2,a)在直线y=-2x+b上,反比例函数y=(x>0)的图象经过点B.
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC,BD.
①如图2,当m=3时,过点D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;
②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三角形,求所有满足条件的m的值.
解:(1)∵点A(0,8)在直线y=-2x+b上,∴-2×0+b=8,∴b=8,∴直线AB的表达式为y=-2x+8,将点B(2,a)代入直线AB的表达式中,得-2×2+8=a,∴a=4,∴B(2,4),将B(2,4)代入反比例函数表达式y=(x>0)中,得k=8 (2)①由(1)知,k=8,∴反比例函数表达式为y=,当m=3时,将线段AB向右平移3个单位长度,得到对应线段CD,∴D(5,4),∵DF⊥x轴于点F,交反比例函数y=的图象于点E,∴E(5,),∴DE=4-=,EF=,∴==
②如图,连接BC,∵将线段AB向右平移m个单位长度(m>0),得到对应线段CD,∴CD=AB,AC=BD=m,∵A(0,8),B(2,4),∴C(m,8),D(m+2,4),∵△BCD是以BC为腰的等腰三角形,∴(Ⅰ)当BC=CD时,BC=AB,∴点B在线段AC的垂直平分线上,∴m=2×2=4;(Ⅱ)当BC=BD时,∵B(2,4),C(m,8),∴BC=,∴=m,解得m=5,综上所述,若△BCD是以BC为腰的等腰三角形时,满足条件的m的值为4或5
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列函数中,变量y是x的反比例函数的是( )
A.y= B.y=5x-1 C.y= D.y=+1
2.已知反比例函数的图象经过点(2,-4),那么这个反比例函数的表达式是( )
A.y= B.y=- C.y= D.y=-
3.对于反比例函数y=-,下列说法错误的是( )
A.图象经过点(1,-5) B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小 D.当x>0时,y随x的增大而增大
4.若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数表达式为I= B.蓄电池的电压是18 V
C.当I≤10 A时,R≥3.6 Ω D.当R=6 Ω时,I=4 A
eq \o(\s\up7(),\s\do5(第5题图)) eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图))
6.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0,x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是( )
A.2<x<6 B.2≤x≤6 C.x>2 D.x<6
7.在同一平面直角坐标系中,函数y=kx+1与y=-(k为常数且k≠0)的图象大致是( )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A,B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
9.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,AC⊥x轴于点C,BD⊥x轴于点D,BE⊥y轴于点E,连接AE.若OE=1,OC=OD,AC=AE,则k的值为( )
A.2 B. C. D.2
10.如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图象上,过点A作x轴的垂线,与函数y=-(x>0)的图象交于点C,连接BC交x轴于点D.若点A的横坐标为1,BC=3BD,则点B的横坐标为( )
A. B.2 C. D.3
eq \o(\s\up7(),\s\do5(第10题图)) eq \o(\s\up7(),\s\do5(第14题图)) eq \o(\s\up7(),\s\do5(第15题图))
二、填空题(每小题3分,共15分)
11.在平面直角坐标系xOy中,若反比例函数y=(k≠0)的图象经过点A(1,2)和点B(-1,m),则m的值为__ __.
12.一元二次方程x2-4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1__ _y2(选填“<”“>”或“=”).
13.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,点P(4,3)在反比例函数的图象上,则当力达到10 N时,物体在力的方向上移动的距离是__ __m.
14.如图,过反比例函数y=(k>0,x>0)图象上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为 .
15.如图,反比例函数y=(k>0)在第一象限的图象上有A(1,6),B(3,b)两点,直线AB与x轴相交于点C,D是线段OA上一点.若AD·BC=AB·DO,连接CD,记△ADC,△DOC的面积分别为S1,S2,则S1-S2的值为__ __.
三、解答题(共75分)
16.(8分)已知y是x的反比例函数,并且当x=2时,y=6.
(1)求y关于x的函数表达式;
(2)当x=4时,求y的值.
17.(9分)已知反比例函数y=的图象分别位于第二、四象限,化简:-+.
18.(9分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式;
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
19.(9分)(2022·兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴,垂足为B(3,0),过C(5,0)作CD⊥x轴,交过点B的一次函数y=x+b的图象于点D,交反比例函数的图象于点E,S△AOB=3.
(1)求反比例比数和一次函数的表达式;
(2)求DE的长.
20.(9分)如图,一次函数y=kx+b的图象与x轴正半轴相交于点C,与反比例函数y=-的图象在第二象限相交于点A(-1,m),过点A作AD⊥x轴,垂足为D,且AD=CD.
(1)求一次函数的表达式;
(2)已知点E(a,0)满足CE=CA,求a的值.
21.(10分)如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC.
(1)求直线AB与双曲线的表达式;
(2)求△ABC的面积.
22.(10分)如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A(1,2),B(-2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出满足k1x+b>的x的取值范围;
(3)若点P在线段AB上,且S△AOP∶S△BOP=1∶4,求点P的坐标.
23.(11分)如图1,点A(0,8),点B(2,a)在直线y=-2x+b上,反比例函数y=(x>0)的图象经过点B.
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC,BD.
①如图2,当m=3时,过点D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;
②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三角形,求所有满足条件的m的值.
答案:
第六章检测题(教师版)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列函数中,变量y是x的反比例函数的是( B )
A.y= B.y=5x-1 C.y= D.y=+1
2.已知反比例函数的图象经过点(2,-4),那么这个反比例函数的表达式是( D )
A.y= B.y=- C.y= D.y=-
3.对于反比例函数y=-,下列说法错误的是( C )
A.图象经过点(1,-5) B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小 D.当x>0时,y随x的增大而增大
4.若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( B )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( C )
A.函数表达式为I= B.蓄电池的电压是18 V
C.当I≤10 A时,R≥3.6 Ω D.当R=6 Ω时,I=4 A
eq \o(\s\up7(),\s\do5(第5题图)) eq \o(\s\up7(),\s\do5(第6题图)) eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图))
6.已知一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0,x>0)的图象如图所示,则当y1>y2时,自变量x满足的条件是( A )
A.2<x<6 B.2≤x≤6 C.x>2 D.x<6
7.在同一平面直角坐标系中,函数y=kx+1与y=-(k为常数且k≠0)的图象大致是( A )
eq \o(\s\up7(),\s\do5(A)) eq \o(\s\up7(),\s\do5(B)) eq \o(\s\up7(),\s\do5(C)) eq \o(\s\up7(),\s\do5(D))
8.如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A,B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( D )
A.8 B.9 C.10 D.11
9.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,AC⊥x轴于点C,BD⊥x轴于点D,BE⊥y轴于点E,连接AE.若OE=1,OC=OD,AC=AE,则k的值为( B )
A.2 B. C. D.2
10.如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图象上,过点A作x轴的垂线,与函数y=-(x>0)的图象交于点C,连接BC交x轴于点D.若点A的横坐标为1,BC=3BD,则点B的横坐标为( B )
A. B.2 C. D.3
eq \o(\s\up7(),\s\do5(第10题图)) eq \o(\s\up7(),\s\do5(第14题图)) eq \o(\s\up7(),\s\do5(第15题图))
二、填空题(每小题3分,共15分)
11.在平面直角坐标系xOy中,若反比例函数y=(k≠0)的图象经过点A(1,2)和点B(-1,m),则m的值为__-2__.
12.一元二次方程x2-4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1__>__y2(选填“<”“>”或“=”).
13.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,点P(4,3)在反比例函数的图象上,则当力达到10 N时,物体在力的方向上移动的距离是__1.2__m.
14.如图,过反比例函数y=(k>0,x>0)图象上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为__S1=4S4__.
15.如图,反比例函数y=(k>0)在第一象限的图象上有A(1,6),B(3,b)两点,直线AB与x轴相交于点C,D是线段OA上一点.若AD·BC=AB·DO,连接CD,记△ADC,△DOC的面积分别为S1,S2,则S1-S2的值为__4__.
三、解答题(共75分)
16.(8分)已知y是x的反比例函数,并且当x=2时,y=6.
(1)求y关于x的函数表达式;
(2)当x=4时,求y的值.
解:(1)由题意,设y=(k≠0),当x=2时,y=6.所以k=12,所以y= (2)当x=4时,y=3
17.(9分)已知反比例函数y=的图象分别位于第二、四象限,化简:-+.
解:∵反比例函数y=的图象分别位于第二、第四象限,∴k<0,∴k-1<0,∴原式=+=k+4+=k+4+|k-1|=k+4-k+1=5
18.(9分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).
(1)求v关于t的函数表达式;
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
解:(1)v=
(2)∵要求不超过5小时卸完船上的这批货物,∴t≤5,则v≥=20,答:平均每小时至少要卸货20吨
19.(9分)(2022·兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴,垂足为B(3,0),过C(5,0)作CD⊥x轴,交过点B的一次函数y=x+b的图象于点D,交反比例函数的图象于点E,S△AOB=3.
(1)求反比例比数和一次函数的表达式;
(2)求DE的长.
解:(1)y=;y=x-
(2)∵过C(5,0)作CD⊥x轴,交过点B的一次函数y=x+b的图象于点D,∴当x=5时,y==,y=x-=3,∴E(5,),D(5,3),∴DE=3-=
20.(9分)如图,一次函数y=kx+b的图象与x轴正半轴相交于点C,与反比例函数y=-的图象在第二象限相交于点A(-1,m),过点A作AD⊥x轴,垂足为D,且AD=CD.
(1)求一次函数的表达式;
(2)已知点E(a,0)满足CE=CA,求a的值.
解:(1)∵点A(-1,m)在反比例函数y=-的图象上,∴-m=-2,解得m=2,∴A(-1,2),∵AD⊥x轴,∴AD=2,OD=1,∵CD=AD=2,∴OC=1,∴C(1,0).把点A(-1,2),C(1,0)代入y=kx+b中,得解得∴一次函数的表达式为y=-x+1
(2)在Rt△ADC中,AC==2,∴AC=CE=2,当点E在点C的左侧时,a=1-2,当点E在点C的右侧时,a=1+2,∴a的值为1±2
21.(10分)如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC.
(1)求直线AB与双曲线的表达式;
(2)求△ABC的面积.
解:(1)直线AB的表达式为y=2x+4,双曲线的表达式为y=
(2)过点B作BG∥x轴,过点C作FG∥y轴,FG和BG交于点G,过点B作BE∥y轴,过点A作FA∥x轴,BE和FA交于点E,设直线BO的表达式为y=ax,易知点B(-3,-2),∴-2=-3a,解得a=,∴直线BO的表达式为y=x,联立解得或∴点C的坐标为(3,2),∵点A(1,6),B(-3,-2),C(3,2),∴EB=8,BG=6,CG=4,CF=4,AF=2,AE=4,∴S△ABC=S矩形EBGF-S△AEB-S△BGC-S△AFC=8×6---=48-16-12-4=16
22.(10分)如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A(1,2),B(-2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出满足k1x+b>的x的取值范围;
(3)若点P在线段AB上,且S△AOP∶S△BOP=1∶4,求点P的坐标.
解:(1)∵反比例函数y=经过A(1,2),∴k2=1×2=2,∴反比例函数的表达式为y=,∵B(-2,n)在反比例函数y=的图象上,∴n==-1,∴B(-2,-1),∵直线y=k1x+b经过A(1,2),B(-2,-1),∴解得∴一次函数的表达式为y=x+1 (2)观察图象,k1x+b>的x的取值范围是-2<x<0或x>1 (3)设P(x,x+1),则-2
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC,BD.
①如图2,当m=3时,过点D作DF⊥x轴于点F,交反比例函数图象于点E,求的值;
②在线段AB运动过程中,连接BC,若△BCD是以BC为腰的等腰三角形,求所有满足条件的m的值.
解:(1)∵点A(0,8)在直线y=-2x+b上,∴-2×0+b=8,∴b=8,∴直线AB的表达式为y=-2x+8,将点B(2,a)代入直线AB的表达式中,得-2×2+8=a,∴a=4,∴B(2,4),将B(2,4)代入反比例函数表达式y=(x>0)中,得k=8 (2)①由(1)知,k=8,∴反比例函数表达式为y=,当m=3时,将线段AB向右平移3个单位长度,得到对应线段CD,∴D(5,4),∵DF⊥x轴于点F,交反比例函数y=的图象于点E,∴E(5,),∴DE=4-=,EF=,∴==
②如图,连接BC,∵将线段AB向右平移m个单位长度(m>0),得到对应线段CD,∴CD=AB,AC=BD=m,∵A(0,8),B(2,4),∴C(m,8),D(m+2,4),∵△BCD是以BC为腰的等腰三角形,∴(Ⅰ)当BC=CD时,BC=AB,∴点B在线段AC的垂直平分线上,∴m=2×2=4;(Ⅱ)当BC=BD时,∵B(2,4),C(m,8),∴BC=,∴=m,解得m=5,综上所述,若△BCD是以BC为腰的等腰三角形时,满足条件的m的值为4或5
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
