人教版七年级数学上册 1.4.1 有理数的乘法 第2课时 课件 (共22张PPT)
文档属性
| 名称 | 人教版七年级数学上册 1.4.1 有理数的乘法 第2课时 课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 21:54:18 | ||
图片预览








文档简介
(共22张PPT)
1.4.1 有理数的乘法
第2课时
学习目标
02
掌握乘法的分配律,并能灵活运用.
03
掌握有理数乘法的运算律,并利用运算律简化乘法运算.
01
掌握多个有理数相乘时积的符号法则.
课前检测
填空:
(1)2×(-3)=______; (2)(-6) ×(-4)=______;
(3)2.4×(-5)=______; (4) - =______.
问题一:想一想:2×(-3)×(-4)×(-5)该如何计算呢
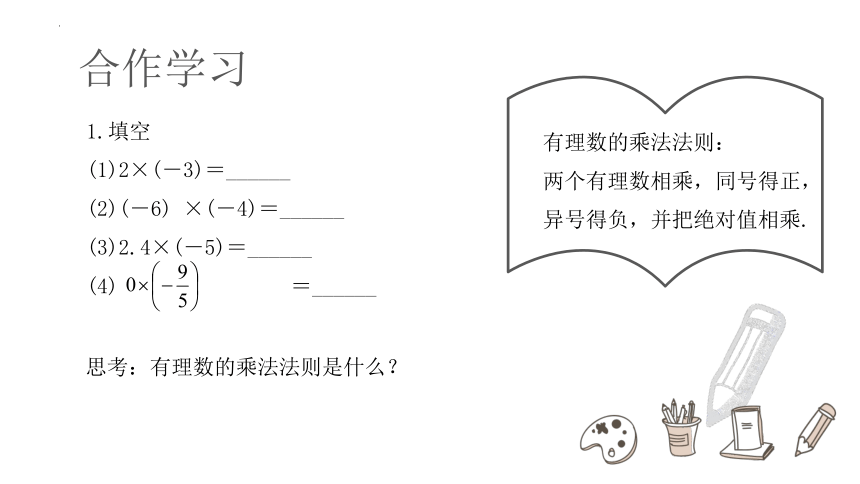
1.填空
(1)2×(-3)=______
(2)(-6) ×(-4)=______
(3)2.4×(-5)=______
(4) =______
合作学习
思考:有理数的乘法法则是什么?
有理数的乘法法则:
两个有理数相乘,同号得正,异号得负,并把绝对值相乘.
合作学习
2. 计算:2×(-3)×(-4)×(-5)
解:原式=(-6)×(-4)×(-5)
=24×(-5)
=-120
运算顺序:从左往右.
合作学习
3.计算:
(1)2×3×4×(-5)
(2)2×3×(-4)×(-5)
(3)2×(-3)×(-4)×(-5)
(4)(-2)×(-3)×(-4)×(-5)
是不是多个因数相乘都有这个规律?
思考:①以上算式的积有什么区别和联系?
②算式的积的符号与什么有关?
合作学习
4.计算:
(1)3×(-5)
(2)3×(-5)×(-2)
(3)3×(-5)×(-2)×(-4)
(4)3×(-5)×(-2)×(-4)×(-3)
(5)3×(-5)×(-2)×(-4)×(-3)×(-6)
归纳:
当负因数个数是奇数时,积为负;
当负因数个数是偶数时,积为正.
思考:(1)算式的积的符号与什么有关?
(2)算式的积的符号与因数有着什么样的关系?
如果出现0呢?
= - 15
= - 120
= 360
=30
= - 2160
合作学习
5.计算:
(1)(-2)×(-3)×0×(-4)
(2)2×0×(-3)×(-4)
思考:根据上面的算式,你能完善问题4中的结论吗?
如果出现0呢?
归纳:
当负因数个数是奇数时,积为负;
当负因数个数是偶数时,积为正.
归纳总结
多个有理数相乘时积的符号法则:
几个不等于0的数相乘, 积的符号由负因数的个数决定. 当负因数有奇数个时, 积为负; 当负因数有偶数个时, 积为正.
几个有理数相乘,有一个因数为0,积就为0.
例1. 计算:
实战演练
解:
原式
解:
原式
1).判断下列各式乘积的符号:
①(-3)×(-4)×(+5.5);
②4×(-2)×(-3.1)×(-7);
③(-301)×0×7×(-2);
④(-3.7)×(-6)×10×(-5.3)×(-1),
其中积为正数的有________,
积为负数的有____________,
积为0的是_______________.(只填写序号)
①④
②
③
2).判断下列各式乘积的符号:
①(-1.25)×(-8)×0×4
② 25×(-0.4)×(-0.1)×(-4)
零
符号为负
测一测
合作学习
6. 请同学们想一想,小学时候我们学过乘法具有哪些运算律 如何验证?
请你计算:
5×(-6)=
(-6)×5=
(-4)×(-3)=
(-3)×(-4)=
-30
-30
12
12
归纳总结
一般地, 有理数乘法中, 两个数相乘, 交换因数的位置, 积相等.
乘法交换律:ab=ba.
思考:这里的a、b可以为哪些数?
实战演练
7.计算:
(1)5×[3+(-7)] (2)5×3+5×(-7)
思考:(1)观察计算结果,从中你发现什么规律?
(2)你能得出什么结论?
解:
=5×(-4)
=-20
原式
解:
=15+(-35)
=-20
原式
归纳总结
一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
思考:这里的a、b可以为哪些数?
分配律:a(b+c)=ab+ac
例题示范
例2. 用两种方法计算:
方法1:原式
=-1
=-1
方法2:原式=3+2-6
测一测
1. 计算:
(1) (-85)×(-25)×(-4)
测一测
解:
测一测
测一测
2. 计算:
测一测
解:
课堂小结
1.多个有理数相乘时积的符号法则:
几个不等于0的数相乘, 积的符号由负因数的个数决定. 当负因数有奇数个时, 积为负; 当负因数有偶数个时, 积为正.
几个有理数相乘,有一个因数为0,积就为0.
2.一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
分配律:a(b+c)=ab+ac
1.4.1 有理数的乘法
第2课时
学习目标
02
掌握乘法的分配律,并能灵活运用.
03
掌握有理数乘法的运算律,并利用运算律简化乘法运算.
01
掌握多个有理数相乘时积的符号法则.
课前检测
填空:
(1)2×(-3)=______; (2)(-6) ×(-4)=______;
(3)2.4×(-5)=______; (4) - =______.
问题一:想一想:2×(-3)×(-4)×(-5)该如何计算呢
1.填空
(1)2×(-3)=______
(2)(-6) ×(-4)=______
(3)2.4×(-5)=______
(4) =______
合作学习
思考:有理数的乘法法则是什么?
有理数的乘法法则:
两个有理数相乘,同号得正,异号得负,并把绝对值相乘.
合作学习
2. 计算:2×(-3)×(-4)×(-5)
解:原式=(-6)×(-4)×(-5)
=24×(-5)
=-120
运算顺序:从左往右.
合作学习
3.计算:
(1)2×3×4×(-5)
(2)2×3×(-4)×(-5)
(3)2×(-3)×(-4)×(-5)
(4)(-2)×(-3)×(-4)×(-5)
是不是多个因数相乘都有这个规律?
思考:①以上算式的积有什么区别和联系?
②算式的积的符号与什么有关?
合作学习
4.计算:
(1)3×(-5)
(2)3×(-5)×(-2)
(3)3×(-5)×(-2)×(-4)
(4)3×(-5)×(-2)×(-4)×(-3)
(5)3×(-5)×(-2)×(-4)×(-3)×(-6)
归纳:
当负因数个数是奇数时,积为负;
当负因数个数是偶数时,积为正.
思考:(1)算式的积的符号与什么有关?
(2)算式的积的符号与因数有着什么样的关系?
如果出现0呢?
= - 15
= - 120
= 360
=30
= - 2160
合作学习
5.计算:
(1)(-2)×(-3)×0×(-4)
(2)2×0×(-3)×(-4)
思考:根据上面的算式,你能完善问题4中的结论吗?
如果出现0呢?
归纳:
当负因数个数是奇数时,积为负;
当负因数个数是偶数时,积为正.
归纳总结
多个有理数相乘时积的符号法则:
几个不等于0的数相乘, 积的符号由负因数的个数决定. 当负因数有奇数个时, 积为负; 当负因数有偶数个时, 积为正.
几个有理数相乘,有一个因数为0,积就为0.
例1. 计算:
实战演练
解:
原式
解:
原式
1).判断下列各式乘积的符号:
①(-3)×(-4)×(+5.5);
②4×(-2)×(-3.1)×(-7);
③(-301)×0×7×(-2);
④(-3.7)×(-6)×10×(-5.3)×(-1),
其中积为正数的有________,
积为负数的有____________,
积为0的是_______________.(只填写序号)
①④
②
③
2).判断下列各式乘积的符号:
①(-1.25)×(-8)×0×4
② 25×(-0.4)×(-0.1)×(-4)
零
符号为负
测一测
合作学习
6. 请同学们想一想,小学时候我们学过乘法具有哪些运算律 如何验证?
请你计算:
5×(-6)=
(-6)×5=
(-4)×(-3)=
(-3)×(-4)=
-30
-30
12
12
归纳总结
一般地, 有理数乘法中, 两个数相乘, 交换因数的位置, 积相等.
乘法交换律:ab=ba.
思考:这里的a、b可以为哪些数?
实战演练
7.计算:
(1)5×[3+(-7)] (2)5×3+5×(-7)
思考:(1)观察计算结果,从中你发现什么规律?
(2)你能得出什么结论?
解:
=5×(-4)
=-20
原式
解:
=15+(-35)
=-20
原式
归纳总结
一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
思考:这里的a、b可以为哪些数?
分配律:a(b+c)=ab+ac
例题示范
例2. 用两种方法计算:
方法1:原式
=-1
=-1
方法2:原式=3+2-6
测一测
1. 计算:
(1) (-85)×(-25)×(-4)
测一测
解:
测一测
测一测
2. 计算:
测一测
解:
课堂小结
1.多个有理数相乘时积的符号法则:
几个不等于0的数相乘, 积的符号由负因数的个数决定. 当负因数有奇数个时, 积为负; 当负因数有偶数个时, 积为正.
几个有理数相乘,有一个因数为0,积就为0.
2.一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
分配律:a(b+c)=ab+ac
