2.3匀变速直线运动的位移与时间的关系 课件(32张PPT)高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 2.3匀变速直线运动的位移与时间的关系 课件(32张PPT)高一上学期物理人教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-30 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
第三节 匀变速直线运动的位移与时间关系
第2章
匀变速直线运动的研究
学习目标
1.了解匀变速直线运动位移与时间的推导过程,掌握位移与时间关系式,并会解决实际物理问题
2.会推导速度与位移关系式,并会解决实际物理问题
3.掌握并运用相关推论
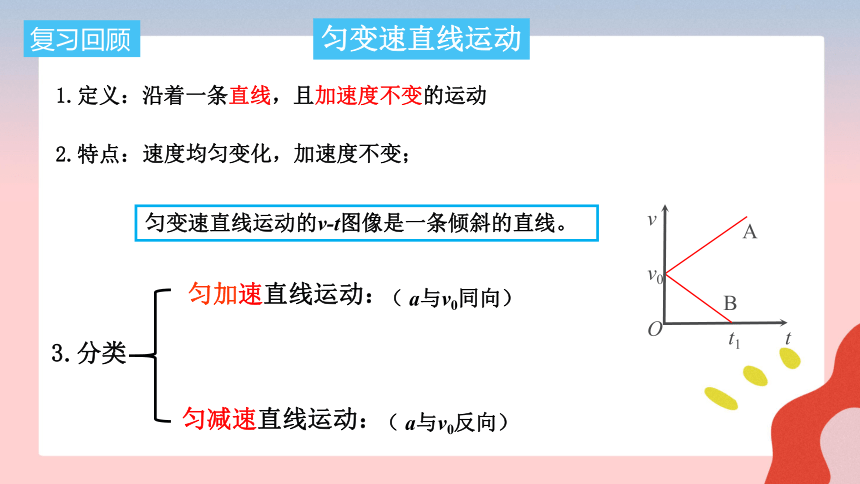
1.定义:沿着一条直线,且加速度不变的运动
2.特点:
速度均匀变化,加速度不变;
匀变速直线运动的v-t图像是一条倾斜的直线。
匀变速直线运动
3.分类
匀加速直线运动:
匀减速直线运动:
( a与v0同向)
( a与v0反向)
v
t
v0
A
B
t1
O
复习回顾
2.适用条件:匀变速直线运动
3.矢量式 一般规定 v0 的方向为正方向
4.特殊情况:(1)当 v 0= 0 时,物体做初速度为零的匀加速直线运动
(2)当 a = 0 时,物体做匀速直线运动
1.公式:
5.注意:刹车问题先求刹车时间
6.关于平均速度的推论:
复习回顾
速度与时间公式
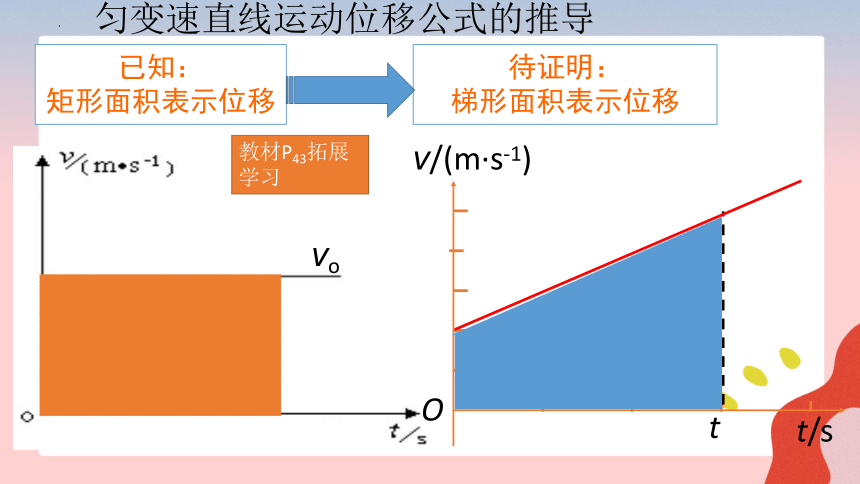
匀变速直线运动位移公式的推导
v/(m·s-1)
O
t
t/s
vo
待证明:
梯形面积表示位移
已知:
矩形面积表示位移
教材P43拓展学习
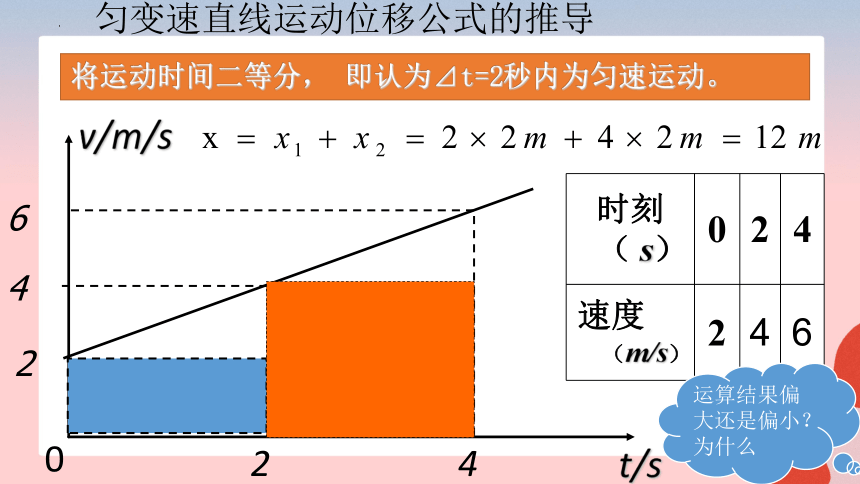
匀变速直线运动位移公式的推导
t/s
v/m/s
2
4
6
0
4
2
将运动时间二等分, 即认为⊿t=2秒内为匀速运动。
时刻( s) 0 2 4
速度(m/s) 2 4 6
运算结果偏大还是偏小?为什么
匀变速直线运动位移公式的推导
1
3
t/s
v/m/s
2
4
6
0
4
2
时刻( s) 0 1 2 3 4
速度(m/s) 2 3 4 5 6
运算结果偏大还是偏小?
将运动时间四等分, 即认为⊿t=1秒内为匀速运动。
匀变速直线运动位移公式的推导
t/s
v/m/s
2
4
6
0
4
2
与前两次运算结果对比有何不同?
X1=12 m x2=14m
时刻s 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
速度(m/s) 2 2.5 3 3.5 4 4.5 5 5.5 6
将运动时间八等分, 即认为⊿t=0.5秒内为匀速运动。
匀变速直线运动位移公式的推导
时间间隔 估算结果
⊿t =2秒 X=12m
⊿t =1秒 x=14m
⊿t =0.5秒 X=15m
在⊿t继续减小时,误差更小,估算值更接近真实值。
如何减小与真实值的差别?
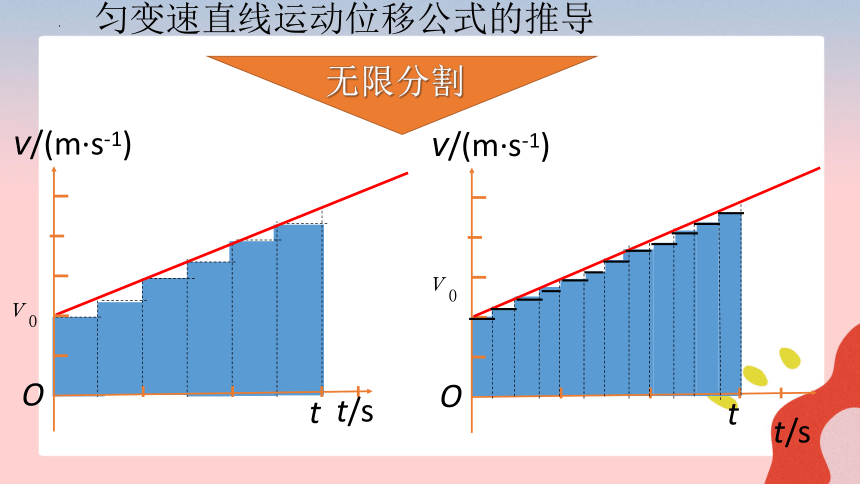
匀变速直线运动位移公式的推导
v/(m·s-1)
O
t
t/s
无限分割
v/(m·s-1)
O
t
t/s
vt = v0+ at
v
t
v0
t
vt
0
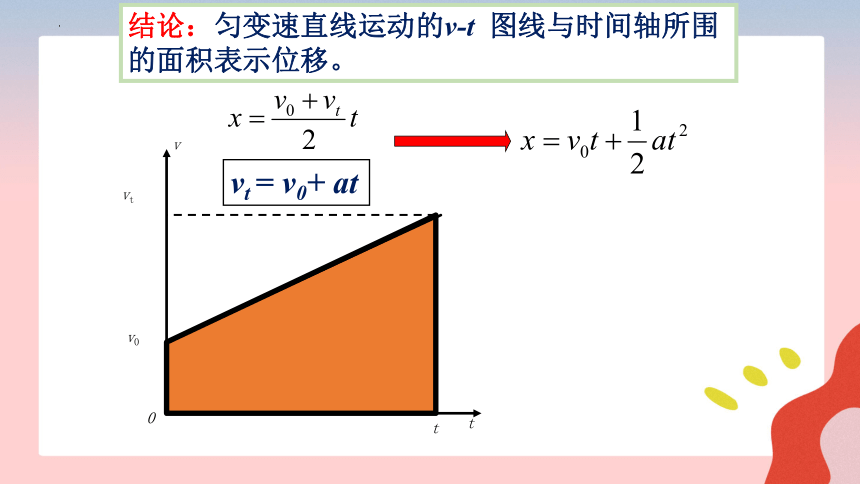
结论:匀变速直线运动的v-t 图线与时间轴所围的面积表示位移。
君子坦荡荡,小人长戚戚
匀变速直线运动的位移
1.公式:
2.对位移公式的理解:
(1)只适用于匀变速直线运动;
(2)因为υ0、α、x均为矢量,使用公式时应先规定正方向。
(一般以υ0的方向为正方向)
(3)若v0=0,
思考与讨论
(1)运用初中数学课本中学过的函数图像的知识,你能画出初速度为0的匀变速直线运动 的x-t图像吗?
(2)我们研究的是直线运动,为什么你画出来的x-t图像不是直线呢?
v0
v
0
t
v0
v
0
t
v0
v
0
t
v0
v
0
t
在每一小段内,可粗略认为物体做匀速直线运动。
各段位移可以用一个又窄又高的小矩形的面积代表。
小矩形的面积之和近似地代表物体在整个运动过程中的位移。
微元求和
t时间内位移等于图像中的梯形面积
这种分析问题的方法具有一般意义,原则上对于处理任意形状的v-t图像都适用。
题型 位移与时间关系式的直接应用
例 某物体从静止开始做匀加速直线运动,加速度为,求:
(1)物体在2 s内的位移大小;
(2)物体在第2 s内的位移大小;
(3)物体在第二个2 s内的位移大小.
练直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
说明刹车后7 .5s汽车停止运动。
车的位移
解:设车实际运动时间为t0,去汽车初速方向为正方向,则:v0= 15m/s,a = - 2m/
由
得运动时间
所以由
刹车问题!
题型 匀变速直线运动的多过程问题
例 滑雪运动员不借助滑雪杖,以加速度a1由静止从坡顶沿直线匀加速滑下,测得20s后的速度为20m/s,50s时到达坡底,又以加速度a2沿水平面匀减速运动25s后停止.求:
(1)a1和a2的大小;
(2)运动员到达坡底后再经过6 s时的速度大小;
(3)运动员在水平面上滑行的距离。
应用位移公式x=v0t+at2解题的基本思路
(1)确定研究对象,并分析判断物体是否做匀变速直线运动.
(2)选择研究过程.
(3)分清已知量和待求量,找出与所选研究过程相对应的v0、a、t、x的值,特别要注意v0并不一定是物体运动的初速度,而是与研究过程相对应的初速度.
(4)规定正方向,判定各矢量的正、负,然后代入公式.
(5)统一已知量的单位,求解方程.
推导匀变速直线运动的位移公式
如图,已知加速度为a,可得到位移是为多少?
(用图中所给物理量表示)
还可以得到怎样的关系式?
可不可以通过速度公式和位移公式
消掉时间t从而直接找出位移与速度之间的关系呢?
思考
速度与位移的关系
推导 :
消去t后解得:
一定要亲自动手啊
注意
1.该公式只适用匀变速直线运动
2.该公式是矢量式,有大小和方向
3.因为v0、v、a、x均为矢量,使用公式时应先规定正方向。
(一般以v0的方向为正方向)若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值.
推论:
速度与位移的关系
v2-x图像和x-v2图像
斜率:k=2a
斜率:k=1/2a
【例】随着机动车数量的增加,交通安全问题日益凸显。分析交通违法事例,将警示我们遵守交通法规,珍惜生命。一货车严重超载后的总质量为49t,以54km/h的速率匀速行驶。发现红灯时司机刹车,货车立即做匀减速直线运动,加速度的大小为2.5m/s2(不超载时则为5m/s2)。
(1)若前方无阻挡,问从刹车到停下来此货车在超载及不超载时分别前进多远?
(2)若超载货车刹车时正前方25m处停着一辆小轿车,两车将发生碰撞,求相撞时货车的速度大小。
【训练】某辆赛车在一段直道上做初速度为零的匀加速直线运动,前2s内位移是8m,则( )
A.赛车的加速度是2m/s2
B.赛车的加速度是3m/s2
C.赛车第4s内的位移是32m
D.赛车第4s内的位移是14m
D
【训练】如图所示,一小车从A点由静止开始做匀加速直线运动,若到达B点时速度为v,到达C点时速度为2v,则xAB∶xBC等于( )
A.1∶1 B.1∶2
C.1∶3 D.1∶4
C
1.(位移与时间关系的应用)一质点做初速度为零的匀加速直线运动,第3s内的位移为15m,则( )
A.质点的加速度为6m/s2
B.质点前3s内的平均速度为15m/s
C.质点第3s末的瞬时速度为15m/s
D.质点第5s内的位移为75m
A
2.(v2-v=2ax的应用)一辆汽车在平直公路上以72km/h的速度匀速行驶,遇到紧急情况需要刹车,刹车时加速度大小为4m/s2,则汽车从刹车开始到停止通过的距离为( )
A.20m B.40m
C.50m D.100m
C
3. (位移与时间关系和速度与位移关系的综合应用)可爱的企鹅喜欢在冰面上玩游戏,如图所示,有一企鹅在倾斜冰面上,先以加速度大小为0.5m/s2从冰面底部由静止开始沿直线向上“奔跑”,t=8s时,突然卧倒以肚皮贴着冰面向前以加速度大小为8m/s2减速滑行至最高点,最后又以加速度大小为4m/s2退滑到出发点,完成一次游戏(企鹅在滑动过程中姿势保持不变)。求:
(1)企鹅向上“奔跑”的位移大小及8s末速度大小;
(2)企鹅在冰面向上滑动的最大距离;
(3)企鹅退滑到出发点时的速度大小。(结果可用根式表示)
课堂小结
物理思想方法:极限思想+微元法
位移与速度
υ0、α、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)
位移与时间
第三节 匀变速直线运动的位移与时间关系
第2章
匀变速直线运动的研究
学习目标
1.了解匀变速直线运动位移与时间的推导过程,掌握位移与时间关系式,并会解决实际物理问题
2.会推导速度与位移关系式,并会解决实际物理问题
3.掌握并运用相关推论
1.定义:沿着一条直线,且加速度不变的运动
2.特点:
速度均匀变化,加速度不变;
匀变速直线运动的v-t图像是一条倾斜的直线。
匀变速直线运动
3.分类
匀加速直线运动:
匀减速直线运动:
( a与v0同向)
( a与v0反向)
v
t
v0
A
B
t1
O
复习回顾
2.适用条件:匀变速直线运动
3.矢量式 一般规定 v0 的方向为正方向
4.特殊情况:(1)当 v 0= 0 时,物体做初速度为零的匀加速直线运动
(2)当 a = 0 时,物体做匀速直线运动
1.公式:
5.注意:刹车问题先求刹车时间
6.关于平均速度的推论:
复习回顾
速度与时间公式
匀变速直线运动位移公式的推导
v/(m·s-1)
O
t
t/s
vo
待证明:
梯形面积表示位移
已知:
矩形面积表示位移
教材P43拓展学习
匀变速直线运动位移公式的推导
t/s
v/m/s
2
4
6
0
4
2
将运动时间二等分, 即认为⊿t=2秒内为匀速运动。
时刻( s) 0 2 4
速度(m/s) 2 4 6
运算结果偏大还是偏小?为什么
匀变速直线运动位移公式的推导
1
3
t/s
v/m/s
2
4
6
0
4
2
时刻( s) 0 1 2 3 4
速度(m/s) 2 3 4 5 6
运算结果偏大还是偏小?
将运动时间四等分, 即认为⊿t=1秒内为匀速运动。
匀变速直线运动位移公式的推导
t/s
v/m/s
2
4
6
0
4
2
与前两次运算结果对比有何不同?
X1=12 m x2=14m
时刻s 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
速度(m/s) 2 2.5 3 3.5 4 4.5 5 5.5 6
将运动时间八等分, 即认为⊿t=0.5秒内为匀速运动。
匀变速直线运动位移公式的推导
时间间隔 估算结果
⊿t =2秒 X=12m
⊿t =1秒 x=14m
⊿t =0.5秒 X=15m
在⊿t继续减小时,误差更小,估算值更接近真实值。
如何减小与真实值的差别?
匀变速直线运动位移公式的推导
v/(m·s-1)
O
t
t/s
无限分割
v/(m·s-1)
O
t
t/s
vt = v0+ at
v
t
v0
t
vt
0
结论:匀变速直线运动的v-t 图线与时间轴所围的面积表示位移。
君子坦荡荡,小人长戚戚
匀变速直线运动的位移
1.公式:
2.对位移公式的理解:
(1)只适用于匀变速直线运动;
(2)因为υ0、α、x均为矢量,使用公式时应先规定正方向。
(一般以υ0的方向为正方向)
(3)若v0=0,
思考与讨论
(1)运用初中数学课本中学过的函数图像的知识,你能画出初速度为0的匀变速直线运动 的x-t图像吗?
(2)我们研究的是直线运动,为什么你画出来的x-t图像不是直线呢?
v0
v
0
t
v0
v
0
t
v0
v
0
t
v0
v
0
t
在每一小段内,可粗略认为物体做匀速直线运动。
各段位移可以用一个又窄又高的小矩形的面积代表。
小矩形的面积之和近似地代表物体在整个运动过程中的位移。
微元求和
t时间内位移等于图像中的梯形面积
这种分析问题的方法具有一般意义,原则上对于处理任意形状的v-t图像都适用。
题型 位移与时间关系式的直接应用
例 某物体从静止开始做匀加速直线运动,加速度为,求:
(1)物体在2 s内的位移大小;
(2)物体在第2 s内的位移大小;
(3)物体在第二个2 s内的位移大小.
练直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
说明刹车后7 .5s汽车停止运动。
车的位移
解:设车实际运动时间为t0,去汽车初速方向为正方向,则:v0= 15m/s,a = - 2m/
由
得运动时间
所以由
刹车问题!
题型 匀变速直线运动的多过程问题
例 滑雪运动员不借助滑雪杖,以加速度a1由静止从坡顶沿直线匀加速滑下,测得20s后的速度为20m/s,50s时到达坡底,又以加速度a2沿水平面匀减速运动25s后停止.求:
(1)a1和a2的大小;
(2)运动员到达坡底后再经过6 s时的速度大小;
(3)运动员在水平面上滑行的距离。
应用位移公式x=v0t+at2解题的基本思路
(1)确定研究对象,并分析判断物体是否做匀变速直线运动.
(2)选择研究过程.
(3)分清已知量和待求量,找出与所选研究过程相对应的v0、a、t、x的值,特别要注意v0并不一定是物体运动的初速度,而是与研究过程相对应的初速度.
(4)规定正方向,判定各矢量的正、负,然后代入公式.
(5)统一已知量的单位,求解方程.
推导匀变速直线运动的位移公式
如图,已知加速度为a,可得到位移是为多少?
(用图中所给物理量表示)
还可以得到怎样的关系式?
可不可以通过速度公式和位移公式
消掉时间t从而直接找出位移与速度之间的关系呢?
思考
速度与位移的关系
推导 :
消去t后解得:
一定要亲自动手啊
注意
1.该公式只适用匀变速直线运动
2.该公式是矢量式,有大小和方向
3.因为v0、v、a、x均为矢量,使用公式时应先规定正方向。
(一般以v0的方向为正方向)若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值.
推论:
速度与位移的关系
v2-x图像和x-v2图像
斜率:k=2a
斜率:k=1/2a
【例】随着机动车数量的增加,交通安全问题日益凸显。分析交通违法事例,将警示我们遵守交通法规,珍惜生命。一货车严重超载后的总质量为49t,以54km/h的速率匀速行驶。发现红灯时司机刹车,货车立即做匀减速直线运动,加速度的大小为2.5m/s2(不超载时则为5m/s2)。
(1)若前方无阻挡,问从刹车到停下来此货车在超载及不超载时分别前进多远?
(2)若超载货车刹车时正前方25m处停着一辆小轿车,两车将发生碰撞,求相撞时货车的速度大小。
【训练】某辆赛车在一段直道上做初速度为零的匀加速直线运动,前2s内位移是8m,则( )
A.赛车的加速度是2m/s2
B.赛车的加速度是3m/s2
C.赛车第4s内的位移是32m
D.赛车第4s内的位移是14m
D
【训练】如图所示,一小车从A点由静止开始做匀加速直线运动,若到达B点时速度为v,到达C点时速度为2v,则xAB∶xBC等于( )
A.1∶1 B.1∶2
C.1∶3 D.1∶4
C
1.(位移与时间关系的应用)一质点做初速度为零的匀加速直线运动,第3s内的位移为15m,则( )
A.质点的加速度为6m/s2
B.质点前3s内的平均速度为15m/s
C.质点第3s末的瞬时速度为15m/s
D.质点第5s内的位移为75m
A
2.(v2-v=2ax的应用)一辆汽车在平直公路上以72km/h的速度匀速行驶,遇到紧急情况需要刹车,刹车时加速度大小为4m/s2,则汽车从刹车开始到停止通过的距离为( )
A.20m B.40m
C.50m D.100m
C
3. (位移与时间关系和速度与位移关系的综合应用)可爱的企鹅喜欢在冰面上玩游戏,如图所示,有一企鹅在倾斜冰面上,先以加速度大小为0.5m/s2从冰面底部由静止开始沿直线向上“奔跑”,t=8s时,突然卧倒以肚皮贴着冰面向前以加速度大小为8m/s2减速滑行至最高点,最后又以加速度大小为4m/s2退滑到出发点,完成一次游戏(企鹅在滑动过程中姿势保持不变)。求:
(1)企鹅向上“奔跑”的位移大小及8s末速度大小;
(2)企鹅在冰面向上滑动的最大距离;
(3)企鹅退滑到出发点时的速度大小。(结果可用根式表示)
课堂小结
物理思想方法:极限思想+微元法
位移与速度
υ0、α、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)
位移与时间
