2022-2023学年人教版七年级数学下册 8.2.1代入消元法解二元一次方程组 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册 8.2.1代入消元法解二元一次方程组 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 21:57:36 | ||
图片预览







文档简介
(共22张PPT)
1、 什么是二元一次方程?
复习
3、什么是二元一次方程的解?
4、什么是二元一次方程组的解?
2、什么是二元一次方程组?
2
激趣导入
世上无难事,只怕有心人。学习数学并不可怕,可怕的是你缺乏克服困难的勇气。
等量代换
曹冲称象的故事同学们听说过吗?
3
尝试用曹冲的方法来解决下面的数学问题:
把2x+y=16中的y用10-x代换得:
2x+(10-x)=16
1.当y=4,2x+y=16,那么x=
2.当y=10-x,2x+y=16,那么x= y=
激趣导入
3.如何求解下面的二元一次方程组?
①
②
x+y=10
2x+y=16
解二元一次方程组
—— 代入消元法
第一页,共15页。
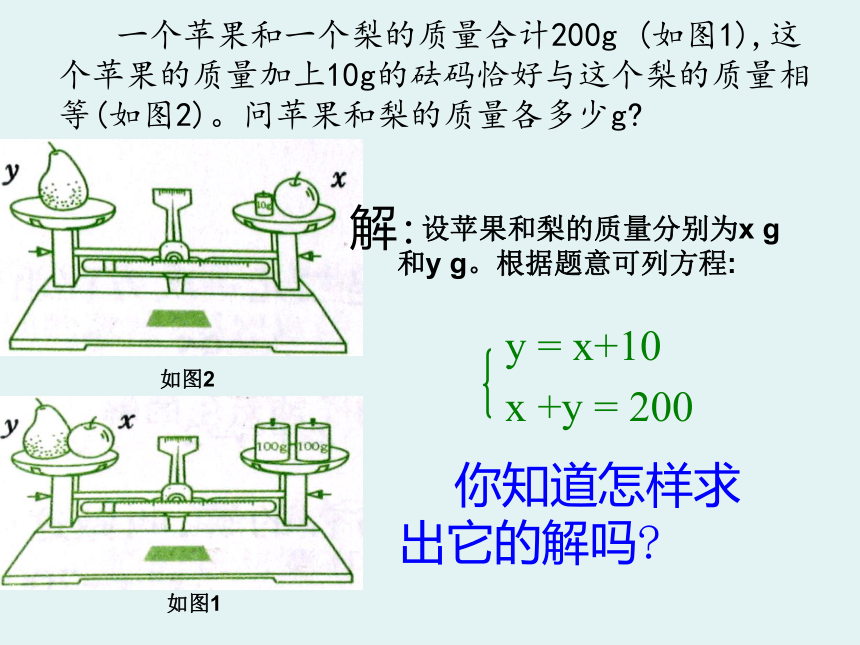
一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g
x +y = 200
y = x+10
你知道怎样求出它的解吗
解:
设苹果和梨的质量分别为x g 和y g。根据题意可列方程:
如图2
如图1
x +y = 200
y = x+10
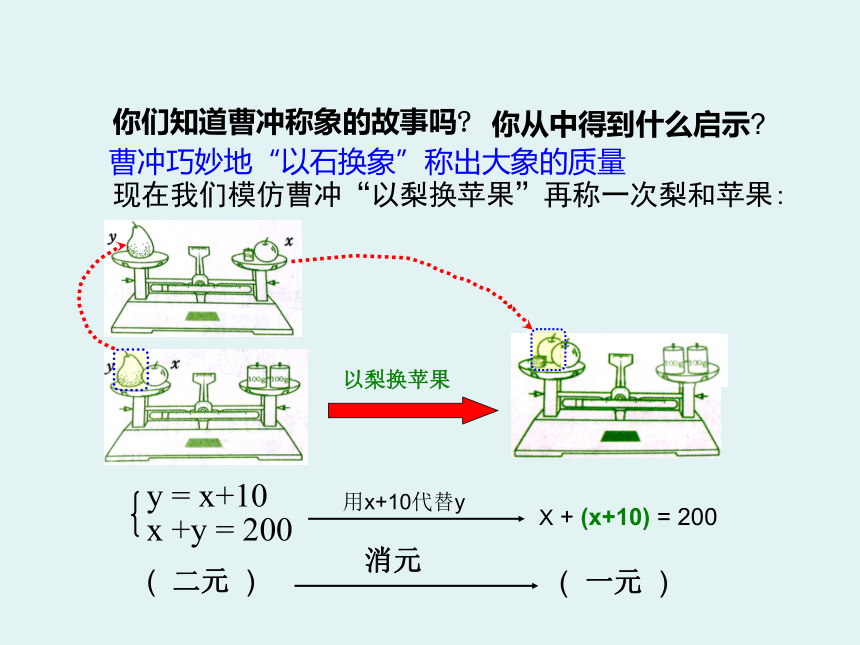
你们知道曹冲称象的故事吗
你从中得到什么启示
曹冲巧妙地“以石换象”称出大象的质量
现在我们模仿曹冲“以梨换苹果”再称一次梨和苹果:
用x+10代替y
X + (x+10) = 200
( 二元 )
( 一元 )
消元
以梨换苹果
即:苹果和梨的质量分别为95g和105g。
x+( x+10)=200
2x+10=200
x = 95
= 95 + 10
= 105
这1个苹果的质量x加上10g的砝码恰好与这1个梨的质量y相等,即X+10与y的大小相等(等量代换)。
解:
为什么可以代入?
∴y = x+10
把①代入②,得:
把x = 95代入①,得:
解方程组的基本思路是“消元”,也是把二元一次方程组化一元一次方程式。
归纳小结
消元的方法是“代入”,这种解方程组的方法称为代入消元法,简称代入法。(它是解二元一次方程常用的方法之一)
预习课本91-92页,探究并解答下面的问题?
1、什么叫消元思想
2、什么叫代入消元法?
把下面的方程,改写成用含x的式子表示y的形式
(1)3x+y=2 (2)2x-5y=3
学
提示:有疑问的组内交流
第三页,共15页。
解:设胜x场,则负(10-x)场.
2x+(10-x)=16.
章引言:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队在10场比赛中得到16分,那么这个队胜负分别是多少?
x+y=10
2x+y=16
设篮球队胜了x场,负了y场。
解:
x + y = 200
y = x+20
解方程组
②
①
y用含x的式子表示
我发现:
当方程组中有一个未知数已经用含另一个未知数的式子表示时,可以直接代入消元。
思考:
具备什么特征的方程组可以直接代入消元?
下列方程组能通过直接代入消元吗?
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
疑问:
需要变形
下列方程组能通过直接代入消元吗?
x=3+y
y=x-3
变形
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
变形
由①得
由①得
由②得
由②得
疑问:
含y的式子表示x
含x的式子表示y
含y的式子表示x
含x的式子表示y
需要变形
例1 解方程组
①
②
x –y = 3
3x -8 y = 14
解1:
由①得:
③
x = 3+ y
把③代入②,得
3(3+ y )– 8 y = 14
把y = – 1代入③,得
x = 2
y = – 1
x=2
y = -1
∴这个方程组的解是
讲
把③代入① 可以吗?试试看
把y=-1代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对。
解这个方程,得
例1 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程;
3、解一元一次方程,求得一个未知数的值;
5、写出方程组的解。
用代入法解二元一次方程组的一般步骤
①变
②代
③求
⑤写
x –y = 3
3x -8 y = 14
解得:
y= – 1
∴方程组的解是
x =2
y = -1
4、把这个未知数的值代入③,求得另一个未知数的值;
④回代
⑥验
(哪个简单变哪个)
把③代入①可以吗?试试看
把y=-1代入① 或②可以吗?
消元: 二元
一元
同学们,你知道问题出在哪里吗?
解:由①,得 x = y + 3 ③
把③代入①,得
y+3 –y =3
得 3=3
算到这里,小明一声惊叫:
未知数去哪里啦?
繁琐的计算令小芳满头大汗
②
①
解:由②,得 ③
把③代入①,得
……
教室里,小明和小芳正在解方程组,此时:
小明
小芳
想想:为吸取小芳的教训,你认为解方程组时选择哪个方程变形更简便?观察未知数系数的特征。
我发现:选择系数较简单的方程变形,把相应的未知数用含另一个未知数的式子表示出来,然后代入消元,可以简便计算。
②
①
抢答:为简便地解方程组,你会选择哪个方程变形
不用变,把①代入②
变②,由② 得y=3-2x
变①,由① 得y=3x-4
变①,由① 得x=3+y或y=x-3
①
②
①
②
①
②
①
②
用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
比一比,看哪组同学最快解出下列方程组!
1
y = 2x-3 ①
3x+2y=8 ②
2
3x +2y = - 1 ①
3x- y=5 ②
解:把①代入②得
3x+2(2x-3)=8
x=2
将x=2代入①得 y=1
∴原方程组的解为
x=2
y=1
练
解:由②得 y=3x-5 ③
把③ 代入①得
3x+2(3x-5) = - 1
x = 1
将x=1代入②得 y=- 2
∴原方程组的解为
x=1
y=-2
解这个方程,得
解这个方程,得
消元的思想、转化的思想
二元一次方程组
消 元
代入法
一元一次方程
说一说,这节课你学到什么?有什么收获?还有什么疑问?
第十三页,共15页。
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
3x-2y=9
x+2y=3
x=4
y=8
x=5
y=15
x=3
y=0
你解对了吗?
1、用代入消元法解下列方程组
谢谢!
第十五页,共15页。
1、 什么是二元一次方程?
复习
3、什么是二元一次方程的解?
4、什么是二元一次方程组的解?
2、什么是二元一次方程组?
2
激趣导入
世上无难事,只怕有心人。学习数学并不可怕,可怕的是你缺乏克服困难的勇气。
等量代换
曹冲称象的故事同学们听说过吗?
3
尝试用曹冲的方法来解决下面的数学问题:
把2x+y=16中的y用10-x代换得:
2x+(10-x)=16
1.当y=4,2x+y=16,那么x=
2.当y=10-x,2x+y=16,那么x= y=
激趣导入
3.如何求解下面的二元一次方程组?
①
②
x+y=10
2x+y=16
解二元一次方程组
—— 代入消元法
第一页,共15页。
一个苹果和一个梨的质量合计200g (如图1),这个苹果的质量加上10g的砝码恰好与这个梨的质量相等(如图2)。问苹果和梨的质量各多少g
x +y = 200
y = x+10
你知道怎样求出它的解吗
解:
设苹果和梨的质量分别为x g 和y g。根据题意可列方程:
如图2
如图1
x +y = 200
y = x+10
你们知道曹冲称象的故事吗
你从中得到什么启示
曹冲巧妙地“以石换象”称出大象的质量
现在我们模仿曹冲“以梨换苹果”再称一次梨和苹果:
用x+10代替y
X + (x+10) = 200
( 二元 )
( 一元 )
消元
以梨换苹果
即:苹果和梨的质量分别为95g和105g。
x+( x+10)=200
2x+10=200
x = 95
= 95 + 10
= 105
这1个苹果的质量x加上10g的砝码恰好与这1个梨的质量y相等,即X+10与y的大小相等(等量代换)。
解:
为什么可以代入?
∴y = x+10
把①代入②,得:
把x = 95代入①,得:
解方程组的基本思路是“消元”,也是把二元一次方程组化一元一次方程式。
归纳小结
消元的方法是“代入”,这种解方程组的方法称为代入消元法,简称代入法。(它是解二元一次方程常用的方法之一)
预习课本91-92页,探究并解答下面的问题?
1、什么叫消元思想
2、什么叫代入消元法?
把下面的方程,改写成用含x的式子表示y的形式
(1)3x+y=2 (2)2x-5y=3
学
提示:有疑问的组内交流
第三页,共15页。
解:设胜x场,则负(10-x)场.
2x+(10-x)=16.
章引言:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队在10场比赛中得到16分,那么这个队胜负分别是多少?
x+y=10
2x+y=16
设篮球队胜了x场,负了y场。
解:
x + y = 200
y = x+20
解方程组
②
①
y用含x的式子表示
我发现:
当方程组中有一个未知数已经用含另一个未知数的式子表示时,可以直接代入消元。
思考:
具备什么特征的方程组可以直接代入消元?
下列方程组能通过直接代入消元吗?
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
疑问:
需要变形
下列方程组能通过直接代入消元吗?
x=3+y
y=x-3
变形
怎样才能直接代入消元?
一个未知数已经用含另一个未知数的式子表示出来。
变形
由①得
由①得
由②得
由②得
疑问:
含y的式子表示x
含x的式子表示y
含y的式子表示x
含x的式子表示y
需要变形
例1 解方程组
①
②
x –y = 3
3x -8 y = 14
解1:
由①得:
③
x = 3+ y
把③代入②,得
3(3+ y )– 8 y = 14
把y = – 1代入③,得
x = 2
y = – 1
x=2
y = -1
∴这个方程组的解是
讲
把③代入① 可以吗?试试看
把y=-1代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对。
解这个方程,得
例1 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程;
3、解一元一次方程,求得一个未知数的值;
5、写出方程组的解。
用代入法解二元一次方程组的一般步骤
①变
②代
③求
⑤写
x –y = 3
3x -8 y = 14
解得:
y= – 1
∴方程组的解是
x =2
y = -1
4、把这个未知数的值代入③,求得另一个未知数的值;
④回代
⑥验
(哪个简单变哪个)
把③代入①可以吗?试试看
把y=-1代入① 或②可以吗?
消元: 二元
一元
同学们,你知道问题出在哪里吗?
解:由①,得 x = y + 3 ③
把③代入①,得
y+3 –y =3
得 3=3
算到这里,小明一声惊叫:
未知数去哪里啦?
繁琐的计算令小芳满头大汗
②
①
解:由②,得 ③
把③代入①,得
……
教室里,小明和小芳正在解方程组,此时:
小明
小芳
想想:为吸取小芳的教训,你认为解方程组时选择哪个方程变形更简便?观察未知数系数的特征。
我发现:选择系数较简单的方程变形,把相应的未知数用含另一个未知数的式子表示出来,然后代入消元,可以简便计算。
②
①
抢答:为简便地解方程组,你会选择哪个方程变形
不用变,把①代入②
变②,由② 得y=3-2x
变①,由① 得y=3x-4
变①,由① 得x=3+y或y=x-3
①
②
①
②
①
②
①
②
用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
比一比,看哪组同学最快解出下列方程组!
1
y = 2x-3 ①
3x+2y=8 ②
2
3x +2y = - 1 ①
3x- y=5 ②
解:把①代入②得
3x+2(2x-3)=8
x=2
将x=2代入①得 y=1
∴原方程组的解为
x=2
y=1
练
解:由②得 y=3x-5 ③
把③ 代入①得
3x+2(3x-5) = - 1
x = 1
将x=1代入②得 y=- 2
∴原方程组的解为
x=1
y=-2
解这个方程,得
解这个方程,得
消元的思想、转化的思想
二元一次方程组
消 元
代入法
一元一次方程
说一说,这节课你学到什么?有什么收获?还有什么疑问?
第十三页,共15页。
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
3x-2y=9
x+2y=3
x=4
y=8
x=5
y=15
x=3
y=0
你解对了吗?
1、用代入消元法解下列方程组
谢谢!
第十五页,共15页。
