梯形表格式讲义五年级上册数学苏教版
图片预览


文档简介
运用梯形的面积公式解决与面积有关的实际问题
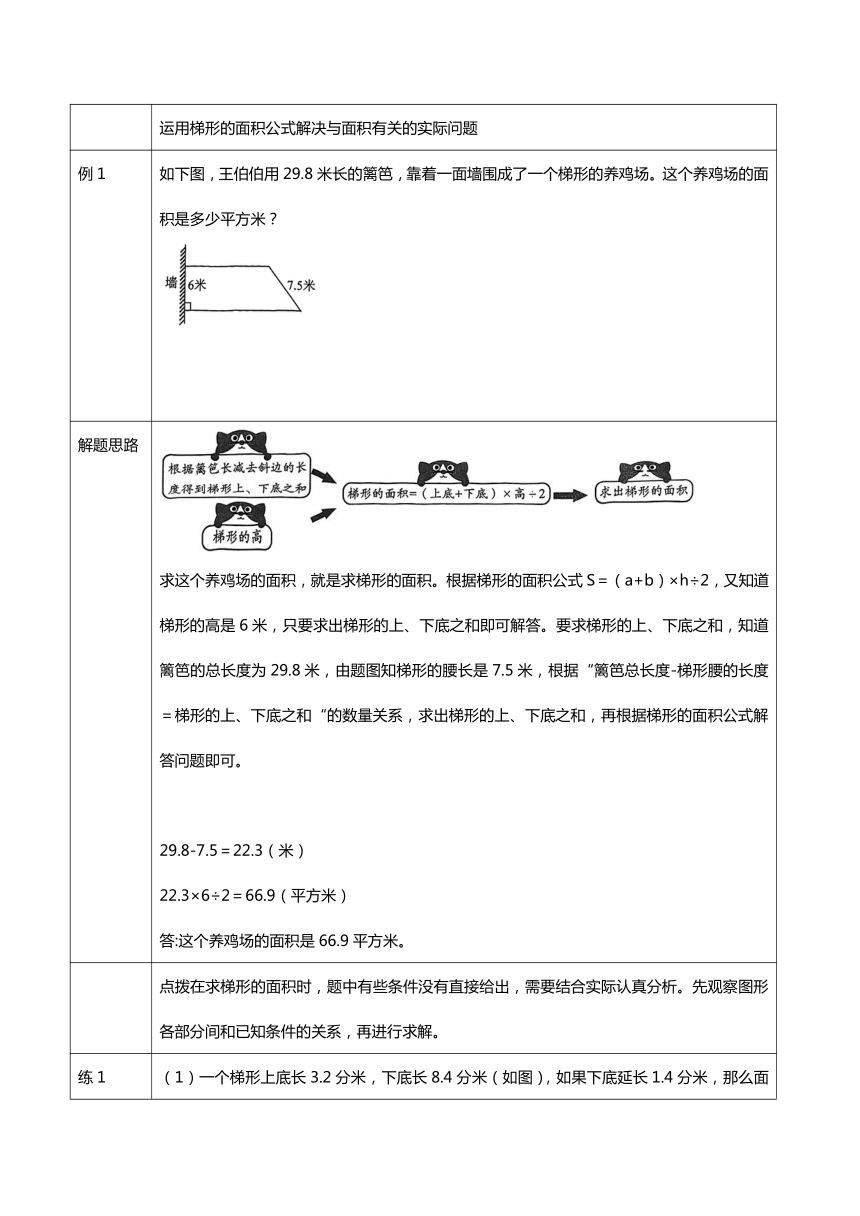
例1 如下图,王伯伯用29.8米长的篱笆,靠着一面墙围成了一个梯形的养鸡场。这个养鸡场的面积是多少平方米?
解题思路 求这个养鸡场的面积,就是求梯形的面积。根据梯形的面积公式S=(a+b)×h÷2,又知道梯形的高是6米,只要求出梯形的上、下底之和即可解答。要求梯形的上、下底之和,知道篱笆的总长度为29.8米,由题图知梯形的腰长是7.5米,根据“篱笆总长度-梯形腰的长度=梯形的上、下底之和“的数量关系,求出梯形的上、下底之和,再根据梯形的面积公式解答问题即可。 29.8-7.5=22.3(米) 22.3×6÷2=66.9(平方米) 答:这个养鸡场的面积是66.9平方米。
点拨在求梯形的面积时,题中有些条件没有直接给出,需要结合实际认真分析。先观察图形各部分间和已知条件的关系,再进行求解。
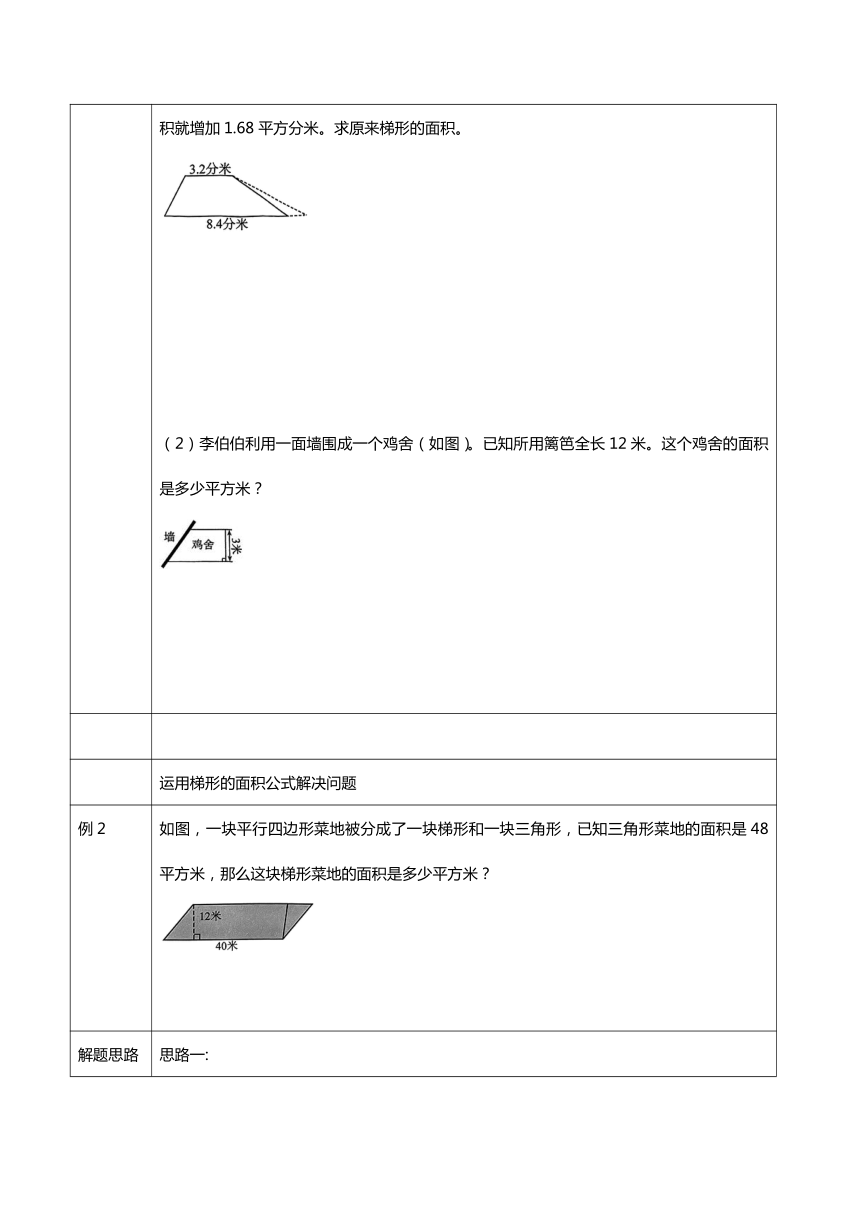
练1 (1)一个梯形上底长3.2分米,下底长8.4分米(如图),如果下底延长1.4分米,那么面积就增加1.68平方分米。求原来梯形的面积。 (2)李伯伯利用一面墙围成一个鸡舍(如图)。已知所用篱笆全长12米。这个鸡舍的面积是多少平方米?
运用梯形的面积公式解决问题
例2 如图,一块平行四边形菜地被分成了一块梯形和一块三角形,已知三角形菜地的面积是48平方米,那么这块梯形菜地的面积是多少平方米?
解题思路 思路一: 根据三角形的面积公式S=ah÷2,得a=2S+h,据此求出三角形的底;平行四边形的底减去三角形的底就是梯形的上底,再根据梯形的面积公式S=(a+b)×h÷2,把数据代入公式解答即可。 思路二: 根据平行四边形的面积公式S=ah,据此求出平行四边形的面积,再根据“梯形的面积=平行四边形的面积-三角形的面积”的数量关系列式解答即可。 方法一:48×2÷12=8(米) (40-8+40)×12÷2=432(平方米) 方法二:40×12-48=432(平方米) 答:这块梯形菜地的面积是432平方米。
练2 (1)如下图,梯形的面积是300平方厘米,上底是10厘米,下底是20厘米,求阴影部分的面积。 (2)一块梯形的玻璃,量得它的上底是8.5分米,下底是16.5分米,高是7.2分米。如果1平方米玻璃的价钱是45元,那么买这块玻璃需要多少钱? (3)在平行线之间有三个图形(如图),它们的面积相比,( )。 A.① >② >③ B.② >① >③ C.③ >① >② (4)一个梯形的上底是8厘米,下底是14厘米,高是5厘米,在这个梯形里画一个最大的三角形,这个三角形的面积是( )平方厘米。 A.22 B.35 C.55
运用图示法解决求梯形面积的问题
例3 一个直角梯形的上底是16分米,如果上底增加4分米就变成了一个正方形,这个梯形的面积是多少平方分米?
解题思路 (16+4+16)×(16+4)÷2=360(平方分米) 答:这个梯形的面积是360平方分米。
练3 一个梯形,如果上底增加4cm,就变成一个平行四边形;如果上底减少3cm,就变成一个三角形,这时面积比原来减少了9cm2。这个梯形的面积是多少平方厘米?
借鉴梯形面积公式的推导方法计算有规律堆放的物体的数量
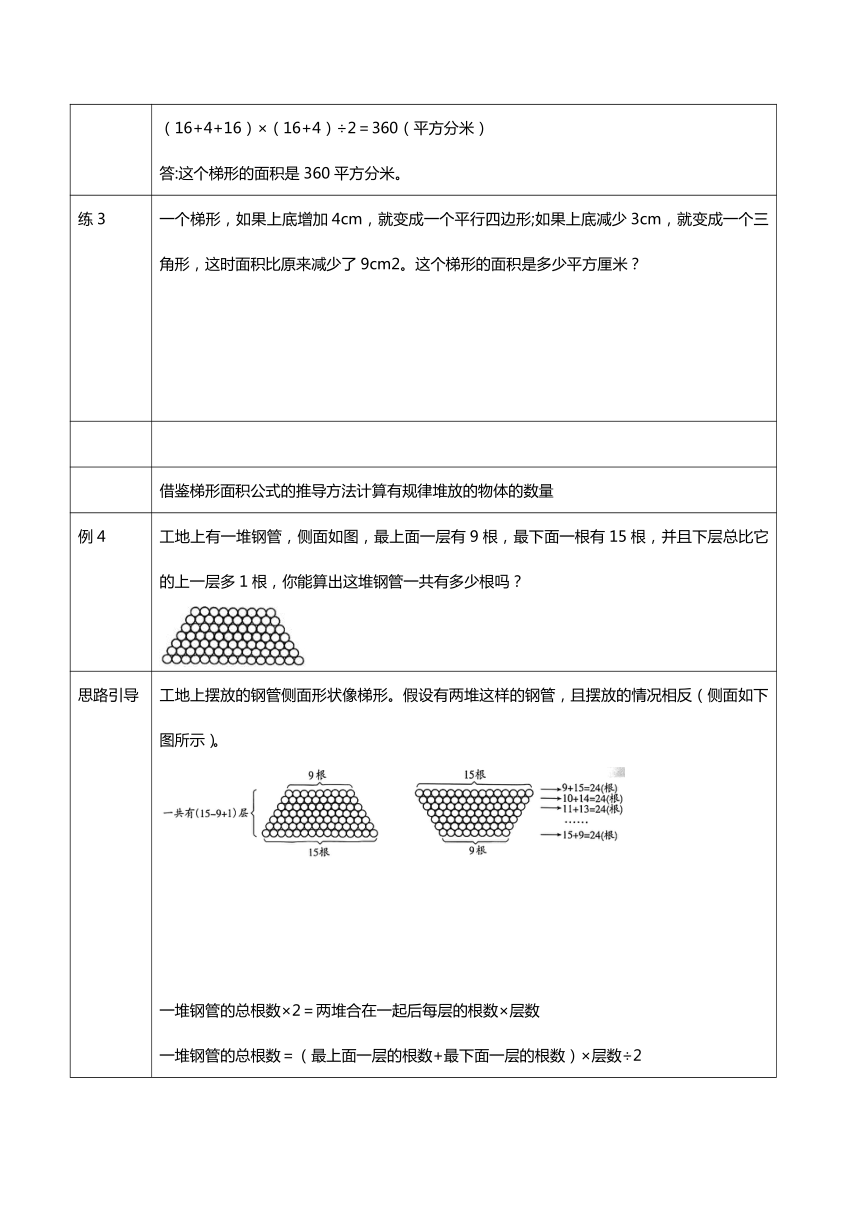
例4 工地上有一堆钢管,侧面如图,最上面一层有9根,最下面一根有15根,并且下层总比它的上一层多1根,你能算出这堆钢管一共有多少根吗?
思路引导 工地上摆放的钢管侧面形状像梯形。假设有两堆这样的钢管,且摆放的情况相反(侧面如下图所示)。 一堆钢管的总根数×2=两堆合在一起后每层的根数×层数 一堆钢管的总根数=(最上面一层的根数+最下面一层的根数)×层数÷2 15-9+1=7(层)(9+15)×7÷2=84(根) 答:这堆钢管一共有84根。
对于这类有规律增加的物体排列问题,可以借鉴梯形面积公式的推导方法求解,数量关系为 “总根数=(最上面一层的根数+最下面一层的根数)×层数÷2”,其中“层数=(最下面一层的根数-最上面一层的根数)÷相邻两层相差的根数+1“。
练4 李爷爷回收了很多空酒瓶,他把这些空酒瓶堆放成了一个近似的梯形。最上层5个,最底层19个,下一层总比上一层多1个。这堆空酒瓶一共有多少个?
运用推理法求梯形的面积
例5 右图是一个直角梯形,较短的一条腰长12厘米,有两条线段把梯形分成了三个三角形,其中两个是等腰直角三角形。这个梯形的面积是多少平方厘米?
解题思路 12×12÷2=144÷2=72(cm2) 答:这个梯形的面积是72cm2。
练5 如图,AB=8cm,CD=14cm,左边的梯形ABCE和右边的三角形CDE面积相等,求梯形ABDE的面积。
例6 把两个完全相同的直角梯形重叠在一起又移开变成如下图形,BE=5厘米,BD= 6厘米,CD=24厘米。求阴影部分的面积。
解题思路 两个完全相同的直角梯形重叠在一起,四边形ABLH是梯形HCDL和梯形GAEF共有的,梯形HCDL-梯形ABLH=梯形GAEF-梯形ABLH,所以阴影部分的面积等于梯形ACDB的面积。根据梯形的面积公式,代入相应的数据进行计算即可。 AB=AE-BE=24-5=19(厘米) S_梯形ACDB=(AB+CD)×BD÷2=(19+24)×6÷2=129(平方厘米) 答:阴影部分的面积是129平方厘米。
在解决图形问题时,很多图形是重叠的,重叠部分图形的面积相等。在求阴影部分的面积时,可以把其替换成与其面积相等的其他图形,这样解题比较方便。两个图形的面积同时减少相同的一部分,它们的差是不变的。
练6 如图,将直角三角形ABC向右平移得到三角形DEF,求图中阴影部分的面积。(单位:厘米)
例7 如图所示,把长方形的长和宽都分别用点平均分成了4份。请用一条线段将长方形分成一个三角形和一个梯形,要求分成的梯形面积是三角形面积的3倍。
从面积公式入手,让梯形的上、下底之和与三角形的底成倍数关系。
解题思路 由梯形的面积公式和三角形的面积公式可得,分成的三角形和梯形的高是相等的,要想使分成的梯形面积是三角形面积的3倍,只要梯形上底与下底的和是三角形底的3倍即可。因为长方形的长和宽都分别用点平均分成了4份,所以从长方形的一个顶点向对边的中点画一条线段,就能使分成的梯形面积是三角形面积的3倍。
梯形和三角形等高的情况下,梯形上底与下底之和是三角形底的几倍,梯形面积就是三角形面积的几倍。
练7 如图,在一个等腰直角三角形中剪去一个三角形后,剩下一个上底为5厘米、下底为10厘米的等腰梯形,求这个等腰梯形的面积。
例1 如下图,王伯伯用29.8米长的篱笆,靠着一面墙围成了一个梯形的养鸡场。这个养鸡场的面积是多少平方米?
解题思路 求这个养鸡场的面积,就是求梯形的面积。根据梯形的面积公式S=(a+b)×h÷2,又知道梯形的高是6米,只要求出梯形的上、下底之和即可解答。要求梯形的上、下底之和,知道篱笆的总长度为29.8米,由题图知梯形的腰长是7.5米,根据“篱笆总长度-梯形腰的长度=梯形的上、下底之和“的数量关系,求出梯形的上、下底之和,再根据梯形的面积公式解答问题即可。 29.8-7.5=22.3(米) 22.3×6÷2=66.9(平方米) 答:这个养鸡场的面积是66.9平方米。
点拨在求梯形的面积时,题中有些条件没有直接给出,需要结合实际认真分析。先观察图形各部分间和已知条件的关系,再进行求解。
练1 (1)一个梯形上底长3.2分米,下底长8.4分米(如图),如果下底延长1.4分米,那么面积就增加1.68平方分米。求原来梯形的面积。 (2)李伯伯利用一面墙围成一个鸡舍(如图)。已知所用篱笆全长12米。这个鸡舍的面积是多少平方米?
运用梯形的面积公式解决问题
例2 如图,一块平行四边形菜地被分成了一块梯形和一块三角形,已知三角形菜地的面积是48平方米,那么这块梯形菜地的面积是多少平方米?
解题思路 思路一: 根据三角形的面积公式S=ah÷2,得a=2S+h,据此求出三角形的底;平行四边形的底减去三角形的底就是梯形的上底,再根据梯形的面积公式S=(a+b)×h÷2,把数据代入公式解答即可。 思路二: 根据平行四边形的面积公式S=ah,据此求出平行四边形的面积,再根据“梯形的面积=平行四边形的面积-三角形的面积”的数量关系列式解答即可。 方法一:48×2÷12=8(米) (40-8+40)×12÷2=432(平方米) 方法二:40×12-48=432(平方米) 答:这块梯形菜地的面积是432平方米。
练2 (1)如下图,梯形的面积是300平方厘米,上底是10厘米,下底是20厘米,求阴影部分的面积。 (2)一块梯形的玻璃,量得它的上底是8.5分米,下底是16.5分米,高是7.2分米。如果1平方米玻璃的价钱是45元,那么买这块玻璃需要多少钱? (3)在平行线之间有三个图形(如图),它们的面积相比,( )。 A.① >② >③ B.② >① >③ C.③ >① >② (4)一个梯形的上底是8厘米,下底是14厘米,高是5厘米,在这个梯形里画一个最大的三角形,这个三角形的面积是( )平方厘米。 A.22 B.35 C.55
运用图示法解决求梯形面积的问题
例3 一个直角梯形的上底是16分米,如果上底增加4分米就变成了一个正方形,这个梯形的面积是多少平方分米?
解题思路 (16+4+16)×(16+4)÷2=360(平方分米) 答:这个梯形的面积是360平方分米。
练3 一个梯形,如果上底增加4cm,就变成一个平行四边形;如果上底减少3cm,就变成一个三角形,这时面积比原来减少了9cm2。这个梯形的面积是多少平方厘米?
借鉴梯形面积公式的推导方法计算有规律堆放的物体的数量
例4 工地上有一堆钢管,侧面如图,最上面一层有9根,最下面一根有15根,并且下层总比它的上一层多1根,你能算出这堆钢管一共有多少根吗?
思路引导 工地上摆放的钢管侧面形状像梯形。假设有两堆这样的钢管,且摆放的情况相反(侧面如下图所示)。 一堆钢管的总根数×2=两堆合在一起后每层的根数×层数 一堆钢管的总根数=(最上面一层的根数+最下面一层的根数)×层数÷2 15-9+1=7(层)(9+15)×7÷2=84(根) 答:这堆钢管一共有84根。
对于这类有规律增加的物体排列问题,可以借鉴梯形面积公式的推导方法求解,数量关系为 “总根数=(最上面一层的根数+最下面一层的根数)×层数÷2”,其中“层数=(最下面一层的根数-最上面一层的根数)÷相邻两层相差的根数+1“。
练4 李爷爷回收了很多空酒瓶,他把这些空酒瓶堆放成了一个近似的梯形。最上层5个,最底层19个,下一层总比上一层多1个。这堆空酒瓶一共有多少个?
运用推理法求梯形的面积
例5 右图是一个直角梯形,较短的一条腰长12厘米,有两条线段把梯形分成了三个三角形,其中两个是等腰直角三角形。这个梯形的面积是多少平方厘米?
解题思路 12×12÷2=144÷2=72(cm2) 答:这个梯形的面积是72cm2。
练5 如图,AB=8cm,CD=14cm,左边的梯形ABCE和右边的三角形CDE面积相等,求梯形ABDE的面积。
例6 把两个完全相同的直角梯形重叠在一起又移开变成如下图形,BE=5厘米,BD= 6厘米,CD=24厘米。求阴影部分的面积。
解题思路 两个完全相同的直角梯形重叠在一起,四边形ABLH是梯形HCDL和梯形GAEF共有的,梯形HCDL-梯形ABLH=梯形GAEF-梯形ABLH,所以阴影部分的面积等于梯形ACDB的面积。根据梯形的面积公式,代入相应的数据进行计算即可。 AB=AE-BE=24-5=19(厘米) S_梯形ACDB=(AB+CD)×BD÷2=(19+24)×6÷2=129(平方厘米) 答:阴影部分的面积是129平方厘米。
在解决图形问题时,很多图形是重叠的,重叠部分图形的面积相等。在求阴影部分的面积时,可以把其替换成与其面积相等的其他图形,这样解题比较方便。两个图形的面积同时减少相同的一部分,它们的差是不变的。
练6 如图,将直角三角形ABC向右平移得到三角形DEF,求图中阴影部分的面积。(单位:厘米)
例7 如图所示,把长方形的长和宽都分别用点平均分成了4份。请用一条线段将长方形分成一个三角形和一个梯形,要求分成的梯形面积是三角形面积的3倍。
从面积公式入手,让梯形的上、下底之和与三角形的底成倍数关系。
解题思路 由梯形的面积公式和三角形的面积公式可得,分成的三角形和梯形的高是相等的,要想使分成的梯形面积是三角形面积的3倍,只要梯形上底与下底的和是三角形底的3倍即可。因为长方形的长和宽都分别用点平均分成了4份,所以从长方形的一个顶点向对边的中点画一条线段,就能使分成的梯形面积是三角形面积的3倍。
梯形和三角形等高的情况下,梯形上底与下底之和是三角形底的几倍,梯形面积就是三角形面积的几倍。
练7 如图,在一个等腰直角三角形中剪去一个三角形后,剩下一个上底为5厘米、下底为10厘米的等腰梯形,求这个等腰梯形的面积。
