三角形(讲义)-五年级上册数学苏教版
文档属性
| 名称 | 三角形(讲义)-五年级上册数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 469.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-30 09:56:37 | ||
图片预览


文档简介
运用平行四边形与三角形面积之间的关系解决问题
例1 如下图所示,已知三角形ABC的面积是6.8平方米。求平行四边形BCDE的面积。
解题思路 根据“三角形ABC的面积是6.8平方米”可知ah÷2=6.8。 观察图形可知,三角形ABC和平行四边形BCDE的底是同一条为BC; 由于平行线间的距离处处相等,因此三角形ABC和平行四边形BCDE的高相等。 再根据S(平行四边形)=ah,因此ah=6.8×2=13.6(平方米),即平行四边形BCDE的面积。 6.8×2=13.6(平方米) 答:平行四边形BCDE的面积是13.6平方米。
注意:等底等高的平行四边形的面积是三角形面积的2倍。
练1 (1)一个平行四边形花坛的面积是57.6平方米,与它等底等高的三角形的高是18米,求这个三角形的底。 (2)一个三角形的底是2.5厘米,高是2.8厘米,这个三角形的面积是( )平方厘米,与它等底等高的平行四边形面积是( )平方厘米。 (3)一个直角三角形它的三条边分别是6厘米、8厘米和10厘米,这个三角形的面积是( )平方厘米。 (4)一个三角形与一个平行四边形的面积相等,高也相等,如果三角形的底是12厘米,那么平行四边形的底是( )厘米。 (5)张爷爷家有一个形状近似于三角形的果园,它的底是180米,高40米。如果每10平方米栽1棵果树,那么这个果园可以栽多少棵果树?
运用推理法解决平行线间的三角形面积问题
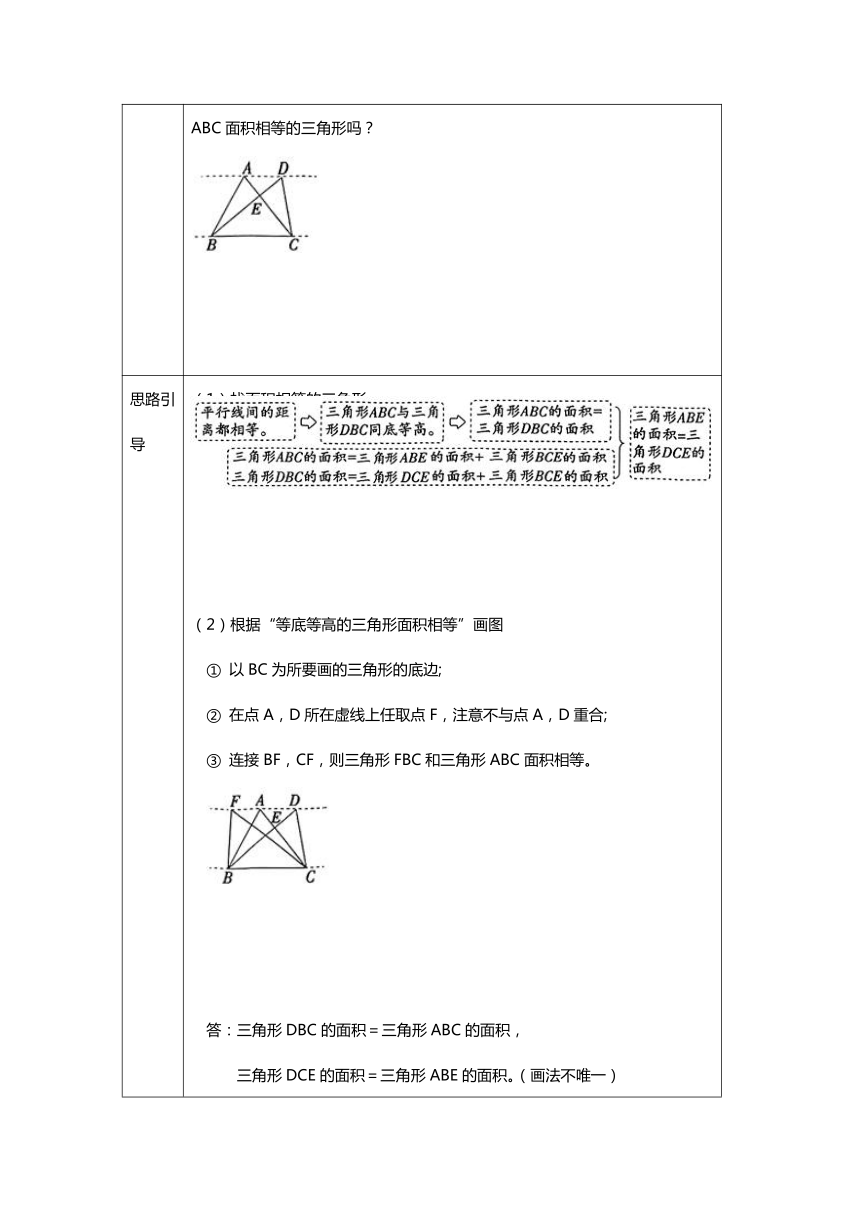
例2 右图中哪几对三角形的面积相等?(两条虚线互相平行)你还能画出和三角形ABC面积相等的三角形吗?
思路引导 (1)找面积相等的三角形 (2)根据“等底等高的三角形面积相等”画图 ① 以BC为所要画的三角形的底边; ② 在点A,D所在虚线上任取点F,注意不与点A,D重合; ③ 连接BF,CF,则三角形FBC和三角形ABC面积相等。 答:三角形DBC的面积=三角形ABC的面积, 三角形DCE的面积=三角形ABE的面积。(画法不唯一) 如图中的三角形FBC和三角形ABC面积相等。
练2 如图,涂色部分甲的面积为15平方厘米,求涂色部分乙的面积。(AB与DC互相平行)
运用三角形与平行四边形面积之间的关系求涂色部分的面积
例3 图中平行四边形的面积是48m2。A是底边的中点,求涂色三角形的面积。
思路引导 48÷2÷2=12(m2) 答:涂色三角形的面积是12m2。
平行四边形相对的两个角的连线将平行四边形分成两个完全相同的三角形; 三角形底边的中点和对应顶点的连线将三角形分成面积相等的两个三角形。
练3 如图,大三角形的面积是48平方厘米,甲三角形的面积是( )平方厘米。 A.8 B.24 C.16 D.12
巧算七巧板中每块板的面积
例4 如图是用一块七巧板拼成的正方形,边长8厘米。你能算出期中每一块板的面积各是多少平方厘米吗?
思路引导 将大正方形分割成32个同样大的小三角形,分析各图形与小三角形面积之间的关系: 小三角形的面积:(8÷4)×(8÷4)÷2=2(平方厘米) ① 的面积=② 的面积=8个小三角形的面积=2×8=16(平方厘米) ④ 的面积=⑥ 的面积=⑦ 的面积=4个小三角形的面积=2×4=8(平方厘米) ③ 的面积=⑤ 的面积=2个小三角形的面积=2×2=4(平方厘米) 答:图中两个大三角形的面积都是16平方厘米, 中等三角形的面积是8平方厘米, 两个小三角形的面积都是4平方厘米, 平行四边形和正方形的面积都是8平方厘米。
解决这类问题的关键:将图形分割成更小的图形,根据各图形与最小的图形之间的面积关系来计算。
例1 如下图所示,已知三角形ABC的面积是6.8平方米。求平行四边形BCDE的面积。
解题思路 根据“三角形ABC的面积是6.8平方米”可知ah÷2=6.8。 观察图形可知,三角形ABC和平行四边形BCDE的底是同一条为BC; 由于平行线间的距离处处相等,因此三角形ABC和平行四边形BCDE的高相等。 再根据S(平行四边形)=ah,因此ah=6.8×2=13.6(平方米),即平行四边形BCDE的面积。 6.8×2=13.6(平方米) 答:平行四边形BCDE的面积是13.6平方米。
注意:等底等高的平行四边形的面积是三角形面积的2倍。
练1 (1)一个平行四边形花坛的面积是57.6平方米,与它等底等高的三角形的高是18米,求这个三角形的底。 (2)一个三角形的底是2.5厘米,高是2.8厘米,这个三角形的面积是( )平方厘米,与它等底等高的平行四边形面积是( )平方厘米。 (3)一个直角三角形它的三条边分别是6厘米、8厘米和10厘米,这个三角形的面积是( )平方厘米。 (4)一个三角形与一个平行四边形的面积相等,高也相等,如果三角形的底是12厘米,那么平行四边形的底是( )厘米。 (5)张爷爷家有一个形状近似于三角形的果园,它的底是180米,高40米。如果每10平方米栽1棵果树,那么这个果园可以栽多少棵果树?
运用推理法解决平行线间的三角形面积问题
例2 右图中哪几对三角形的面积相等?(两条虚线互相平行)你还能画出和三角形ABC面积相等的三角形吗?
思路引导 (1)找面积相等的三角形 (2)根据“等底等高的三角形面积相等”画图 ① 以BC为所要画的三角形的底边; ② 在点A,D所在虚线上任取点F,注意不与点A,D重合; ③ 连接BF,CF,则三角形FBC和三角形ABC面积相等。 答:三角形DBC的面积=三角形ABC的面积, 三角形DCE的面积=三角形ABE的面积。(画法不唯一) 如图中的三角形FBC和三角形ABC面积相等。
练2 如图,涂色部分甲的面积为15平方厘米,求涂色部分乙的面积。(AB与DC互相平行)
运用三角形与平行四边形面积之间的关系求涂色部分的面积
例3 图中平行四边形的面积是48m2。A是底边的中点,求涂色三角形的面积。
思路引导 48÷2÷2=12(m2) 答:涂色三角形的面积是12m2。
平行四边形相对的两个角的连线将平行四边形分成两个完全相同的三角形; 三角形底边的中点和对应顶点的连线将三角形分成面积相等的两个三角形。
练3 如图,大三角形的面积是48平方厘米,甲三角形的面积是( )平方厘米。 A.8 B.24 C.16 D.12
巧算七巧板中每块板的面积
例4 如图是用一块七巧板拼成的正方形,边长8厘米。你能算出期中每一块板的面积各是多少平方厘米吗?
思路引导 将大正方形分割成32个同样大的小三角形,分析各图形与小三角形面积之间的关系: 小三角形的面积:(8÷4)×(8÷4)÷2=2(平方厘米) ① 的面积=② 的面积=8个小三角形的面积=2×8=16(平方厘米) ④ 的面积=⑥ 的面积=⑦ 的面积=4个小三角形的面积=2×4=8(平方厘米) ③ 的面积=⑤ 的面积=2个小三角形的面积=2×2=4(平方厘米) 答:图中两个大三角形的面积都是16平方厘米, 中等三角形的面积是8平方厘米, 两个小三角形的面积都是4平方厘米, 平行四边形和正方形的面积都是8平方厘米。
解决这类问题的关键:将图形分割成更小的图形,根据各图形与最小的图形之间的面积关系来计算。
