平行四边形的面积(讲义)-五年级上册数学苏教版
文档属性
| 名称 | 平行四边形的面积(讲义)-五年级上册数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-30 10:02:05 | ||
图片预览


文档简介
第二单元:平行四边形的面积
学习目标 1.通过剪、移、拼等方法,探索并掌握平行四边形面积公式的推导过程。 2. 能正确计算平行四边形的面积,会应用公式解决简单的实际问题。 3. 体会等积变形、转化等数学思想方法,发展推理意识。
知识导图
知识点1 运用数方格法和转化法比较图形的面积
题1 下面每组的两个图形面积相等吗?
1、理解题意 题中②和④是规则图形,①和③是不规则图形,可以运用数方格法和转化法比较面积的大小。
2、解决问题,优化方法 方法一:数方格法
方法二:转化法 发现:转化后再比较两个图形的面积更简便。
归纳总结 复杂图形可以转化成简单图形,割补、平移是实现转化的基本方法。转化前后,图形的形状变了,但面积不变。
知识点2 把平行四边形转换成长方形的方法
题2
1、观察特征 把平行四边形转化成长方形关键在于构造直角。
2、探究转化方法 方法一:沿着高剪下一个三角形平移。
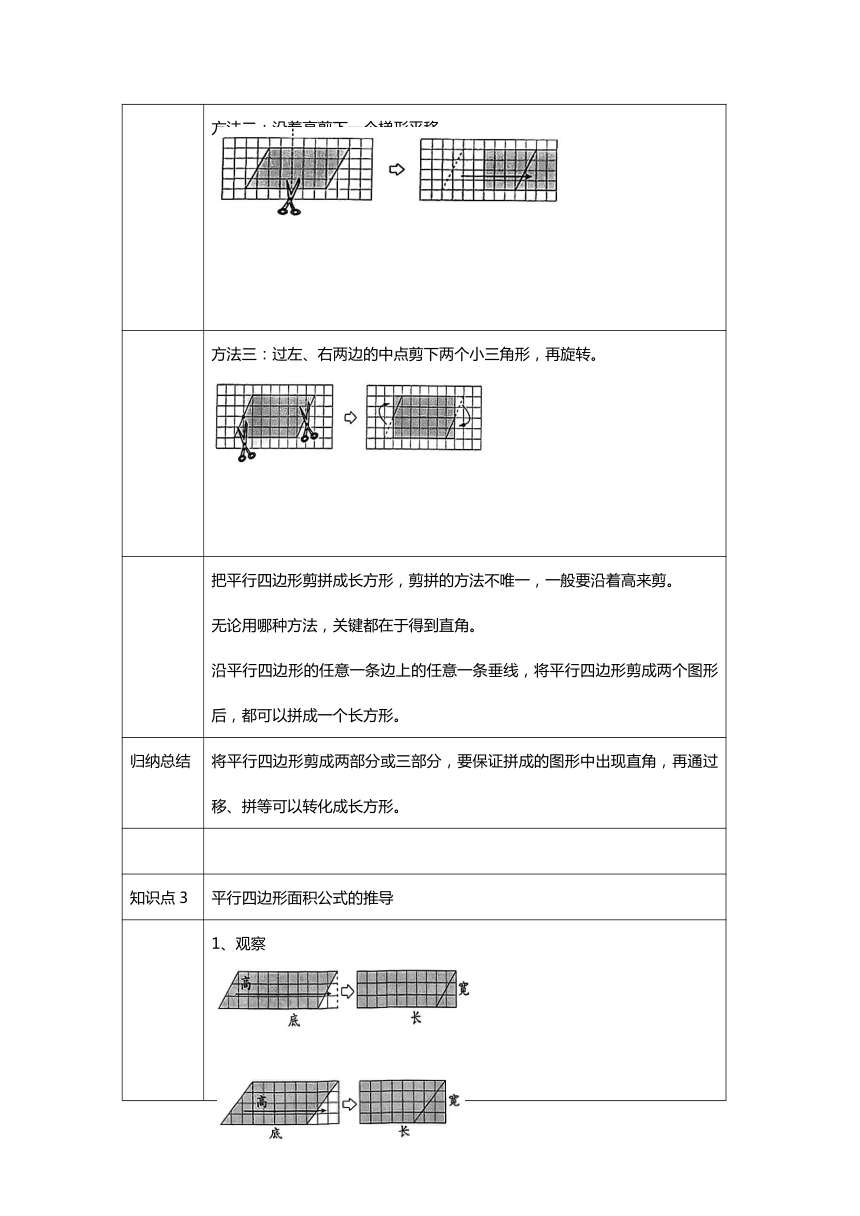
方法二:沿着高剪下一个梯形平移。
方法三:过左、右两边的中点剪下两个小三角形,再旋转。
把平行四边形剪拼成长方形,剪拼的方法不唯一,一般要沿着高来剪。 无论用哪种方法,关键都在于得到直角。 沿平行四边形的任意一条边上的任意一条垂线,将平行四边形剪成两个图形后,都可以拼成一个长方形。
归纳总结 将平行四边形剪成两部分或三部分,要保证拼成的图形中出现直角,再通过移、拼等可以转化成长方形。
知识点3 平行四边形面积公式的推导
1、观察
2、发现 (1)转化成的长方形和原来的平行四边形的面积相等。 (2)长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高。
3、推导平行四边形的面积计算公式 如果用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么平行四边形的面积公式可以写成: S=a×h
归纳总结 1、平行四边形的面积=底×高,用字母表示是:S=a×h。 2、等底等高的平行四边形面积相等。
知识点4 平行四边形面积公式的应用
应用一 已知平行四边形的底和高,求面积
一块平行四边形玻璃,底50厘米,高70厘米,面积是多少平方厘米?
1、理解题意 玻璃的形状是平行四边形,且已知底和高,可直接根据平行四边形的面积公式S=a×h计算。
2、正确解答 50×70=3500(平方厘米) 答:面积是3500平方厘米。
应用二 已知平行四边形的面积和底(或高),求高(或底)
一个平行四边形的面积是240平方分米,底是2米,这条底边上的高是多少分米?
1、分析题意 由S=a×h推得h=S÷a,代入已知数据即可求出高。
2、正确解答 2米=20分米 240÷20=12(分米) 答:这条底边上的高是12分米。
归纳总结 已知平行四边形的底、高和面积三个量中的任意两个量,都可以求出第三个量,即S=a×h h=S÷a a=S÷h。
练一练 1、菲菲学校里有一个平行四边形花圃(如图所示),学校准备在假期整修这个花圃,需要知道它的面积。这个花圃的面积是( )平方米。
2、一块面积是240平方分米的平行四边形钢板,高是400厘米,底是多少分米?
学习目标 1.通过剪、移、拼等方法,探索并掌握平行四边形面积公式的推导过程。 2. 能正确计算平行四边形的面积,会应用公式解决简单的实际问题。 3. 体会等积变形、转化等数学思想方法,发展推理意识。
知识导图
知识点1 运用数方格法和转化法比较图形的面积
题1 下面每组的两个图形面积相等吗?
1、理解题意 题中②和④是规则图形,①和③是不规则图形,可以运用数方格法和转化法比较面积的大小。
2、解决问题,优化方法 方法一:数方格法
方法二:转化法 发现:转化后再比较两个图形的面积更简便。
归纳总结 复杂图形可以转化成简单图形,割补、平移是实现转化的基本方法。转化前后,图形的形状变了,但面积不变。
知识点2 把平行四边形转换成长方形的方法
题2
1、观察特征 把平行四边形转化成长方形关键在于构造直角。
2、探究转化方法 方法一:沿着高剪下一个三角形平移。
方法二:沿着高剪下一个梯形平移。
方法三:过左、右两边的中点剪下两个小三角形,再旋转。
把平行四边形剪拼成长方形,剪拼的方法不唯一,一般要沿着高来剪。 无论用哪种方法,关键都在于得到直角。 沿平行四边形的任意一条边上的任意一条垂线,将平行四边形剪成两个图形后,都可以拼成一个长方形。
归纳总结 将平行四边形剪成两部分或三部分,要保证拼成的图形中出现直角,再通过移、拼等可以转化成长方形。
知识点3 平行四边形面积公式的推导
1、观察
2、发现 (1)转化成的长方形和原来的平行四边形的面积相等。 (2)长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高。
3、推导平行四边形的面积计算公式 如果用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么平行四边形的面积公式可以写成: S=a×h
归纳总结 1、平行四边形的面积=底×高,用字母表示是:S=a×h。 2、等底等高的平行四边形面积相等。
知识点4 平行四边形面积公式的应用
应用一 已知平行四边形的底和高,求面积
一块平行四边形玻璃,底50厘米,高70厘米,面积是多少平方厘米?
1、理解题意 玻璃的形状是平行四边形,且已知底和高,可直接根据平行四边形的面积公式S=a×h计算。
2、正确解答 50×70=3500(平方厘米) 答:面积是3500平方厘米。
应用二 已知平行四边形的面积和底(或高),求高(或底)
一个平行四边形的面积是240平方分米,底是2米,这条底边上的高是多少分米?
1、分析题意 由S=a×h推得h=S÷a,代入已知数据即可求出高。
2、正确解答 2米=20分米 240÷20=12(分米) 答:这条底边上的高是12分米。
归纳总结 已知平行四边形的底、高和面积三个量中的任意两个量,都可以求出第三个量,即S=a×h h=S÷a a=S÷h。
练一练 1、菲菲学校里有一个平行四边形花圃(如图所示),学校准备在假期整修这个花圃,需要知道它的面积。这个花圃的面积是( )平方米。
2、一块面积是240平方分米的平行四边形钢板,高是400厘米,底是多少分米?
