第四章 几何初步图形单元测试题 2023-2024学年人教版七年级数学上册(含答案)
文档属性
| 名称 | 第四章 几何初步图形单元测试题 2023-2024学年人教版七年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 492.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 10:20:36 | ||
图片预览


文档简介
第四章 几何初步图形 单元测试题 2023-2024学年人教版七年级数学上册
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
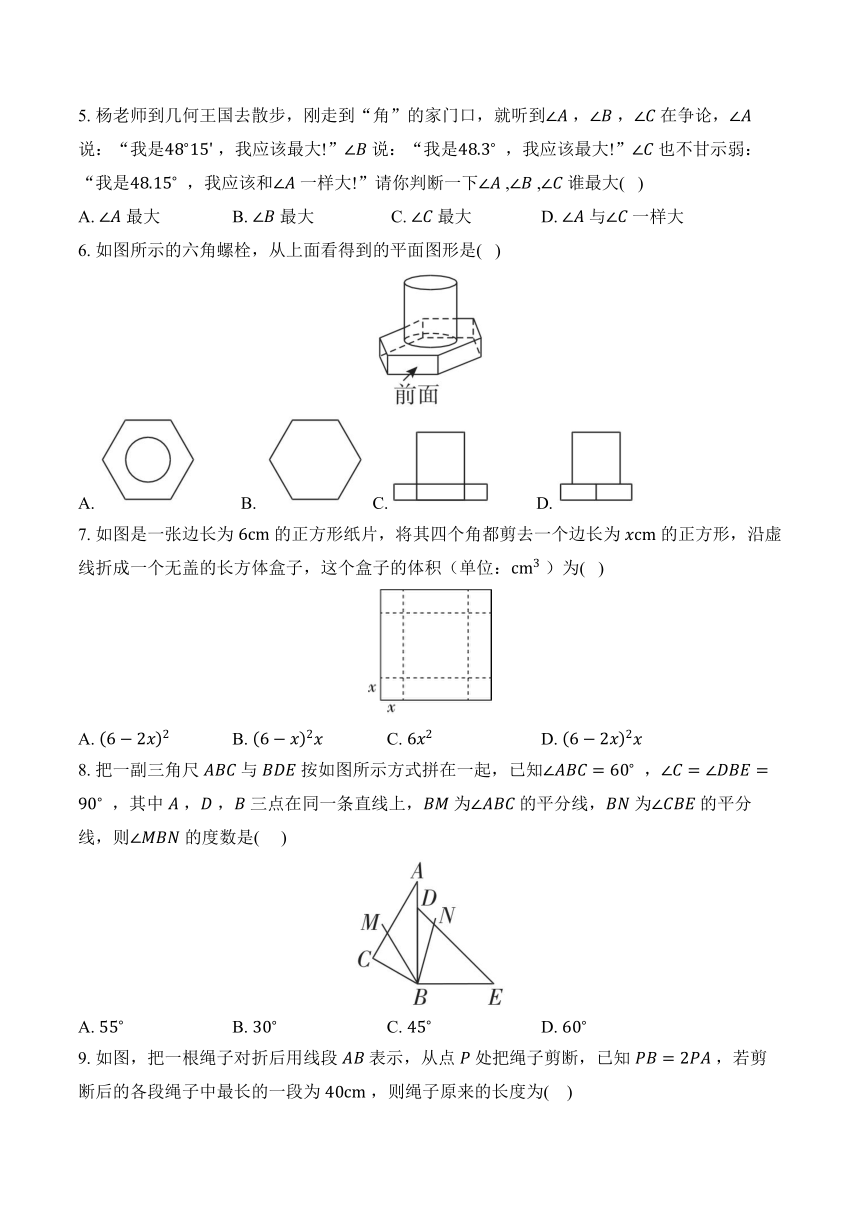
1. 下列四个几何体中,含有曲面的是( )
A. B. C. D.
2. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是( )
A. 四边形周长小于三角形周长 B. 两点确定一条直线
C. 两点之间,线段最短 D. 经过一点有无数条直线
3. 如图,将下面的平面图形绕直线 旋转一周,得到的立体图形是( )
A. B. C. D.
4. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,在原正方体中,与“一”字所在面相对的面上的汉字是( )
A. 亚 B. 洲 C. 体 D. 育
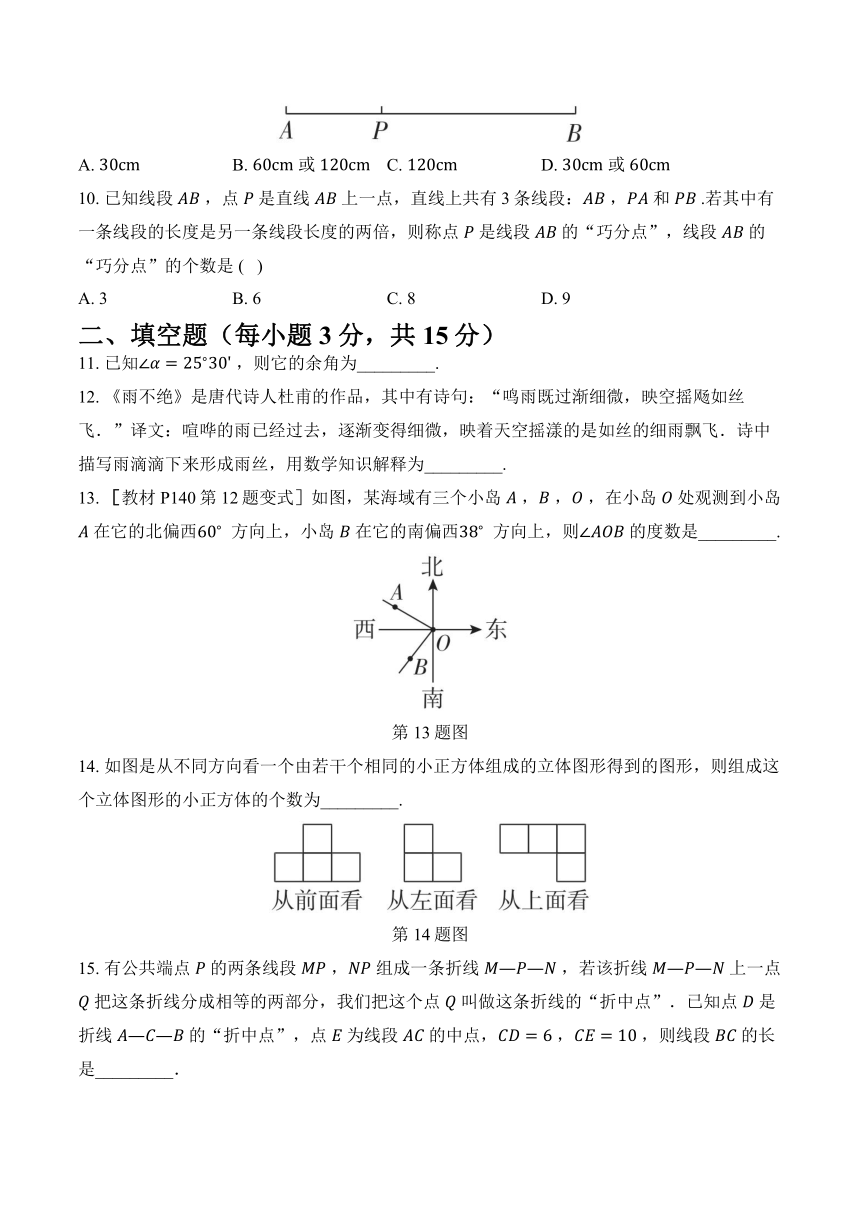
5. 杨老师到几何王国去散步,刚走到“角”的家门口,就听到 , , 在争论, 说:“我是 ,我应该最大!” 说:“我是 ,我应该最大!” 也不甘示弱:“我是 ,我应该和 一样大!”请你判断一下 , , 谁最大( )
A. 最大 B. 最大 C. 最大 D. 与 一样大
6. 如图所示的六角螺栓,从上面看得到的平面图形是( )
A. B. C. D.
7. 如图是一张边长为 的正方形纸片,将其四个角都剪去一个边长为 的正方形,沿虚线折成一个无盖的长方体盒子,这个盒子的体积(单位: )为( )
A. B. C. D.
8. 把一副三角尺 与 按如图所示方式拼在一起,已知 , ,其中 , , 三点在同一条直线上, 为 的平分线, 为 的平分线,则 的度数是( )
A. B. C. D.
9. 如图,把一根绳子对折后用线段 表示,从点 处把绳子剪断,已知 ,若剪断后的各段绳子中最长的一段为 ,则绳子原来的长度为( )
A. B. 或 C. D. 或
10. 已知线段 ,点 是直线 上一点,直线上共有3条线段: , 和 .若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段 的“巧分点”,线段 的“巧分点”的个数是 ( )
A. 3 B. 6 C. 8 D. 9
二、填空题(每小题3分,共15分)
11. 已知 ,则它的余角为_________.
12. 《雨不绝》是唐代诗人杜甫的作品,其中有诗句:“鸣雨既过渐细微,映空摇飏如丝飞.”译文:喧哗的雨已经过去,逐渐变得细微,映着天空摇漾的是如丝的细雨飘飞.诗中描写雨滴滴下来形成雨丝,用数学知识解释为_________.
13. [教材P140第12题变式]如图,某海域有三个小岛 , , ,在小岛 处观测到小岛 在它的北偏西 方向上,小岛 在它的南偏西 方向上,则 的度数是_________.
第13题图
14. 如图是从不同方向看一个由若干个相同的小正方体组成的立体图形得到的图形,则组成这个立体图形的小正方体的个数为_________.
第14题图
15. 有公共端点 的两条线段 , 组成一条折线 ,若该折线 上一点 把这条折线分成相等的两部分,我们把这个点 叫做这条折线的“折中点”.已知点 是折线 的“折中点”,点 为线段 的中点, , ,则线段 的长是_________.
三、解答题(本大题共8个小题,共75分)
16. (8分)计算:
(1) ; (2) .
17. (9分)如图是由一些大小相同的小正方体组合成的简单几何体,根据要求完成下列题目:
(1) 请在下面方格纸中分别画出从左面和从上面看到的平面图形(画出的图需涂上阴影).
(2) 图中共有_________个小正方体.
18. (9分)如图,已知 , , , 四点,根据下列要求画图:
(1) 作直线 ,射线 .
(2) 在射线 上取一点 (点 在线段 上,且不与点 , 重合),画线段 .
(3) 延长线段 至点 ,使 .
19. (9分)如图,已知 .
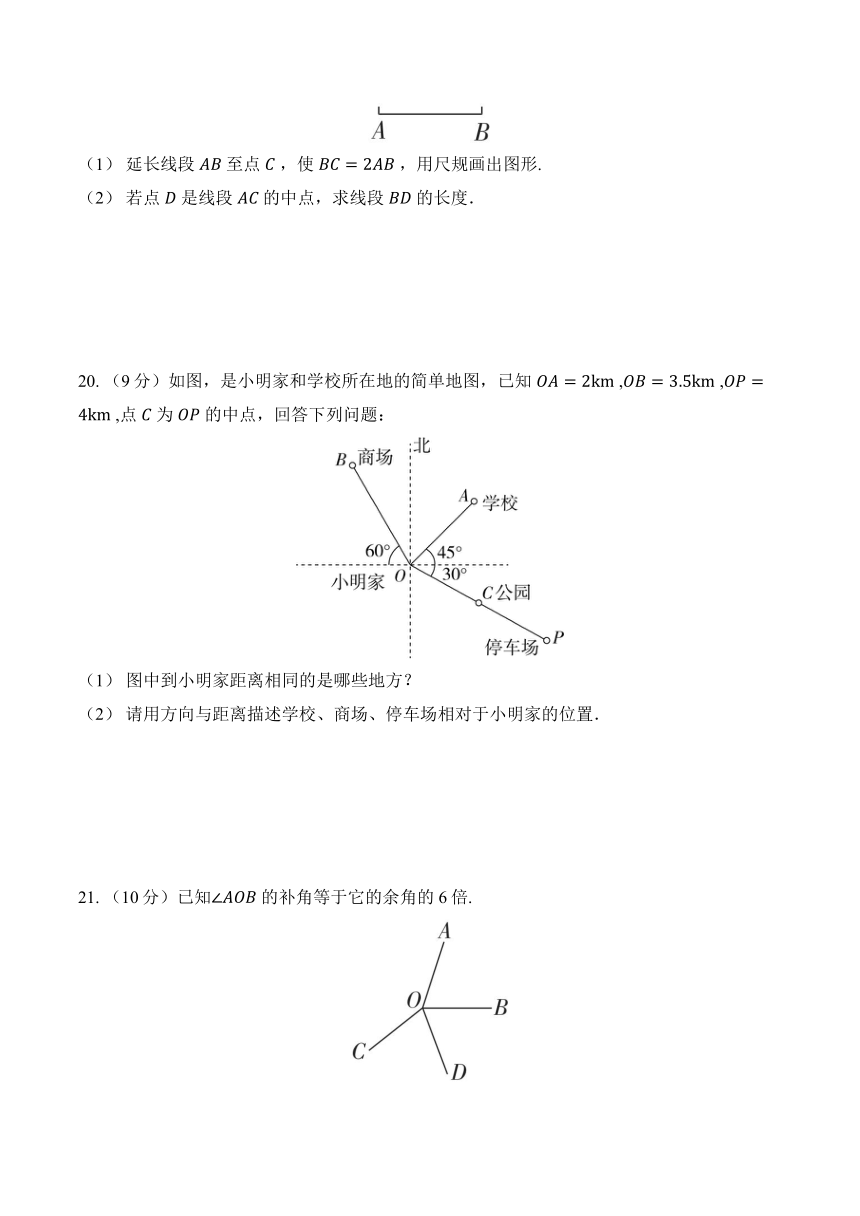
(1) 延长线段 至点 ,使 ,用尺规画出图形.
(2) 若点 是线段 的中点,求线段 的长度.
20. (9分)如图,是小明家和学校所在地的简单地图,已知 , , ,点 为 的中点,回答下列问题:
(1) 图中到小明家距离相同的是哪些地方?
(2) 请用方向与距离描述学校、商场、停车场相对于小明家的位置.
21. (10分)已知 的补角等于它的余角的6倍.
(1) 求 的度数.
(2) 如图,若 平分 , ,求 的度数.
22. (10分)如图, 为线段 上一点, , , , 分别为 , 的中点.
(1) 若 ,求线段 的长.
(2) 若 ,求线段 的长.
23. (11分)如图, 是线段 上任一点, , , 两点分别从 , 同时向 点运动,且 点的运动速度为 , 点的运动速度为 ,运动的时间为 .
(1) 若 .
① 运动 后, 的长为_________;② 当 在线段 上运动时,试说明 .
(2) 当 时,若 ,试探索 的长.
参考答案
第四章 几何初步图形 单元测试题 2023-2024学年人教版七年级数学上册
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1. 下列四个几何体中,含有曲面的是( A )
A. B.
C. D.
2. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是( C )
A. 四边形周长小于三角形周长 B. 两点确定一条直线
C. 两点之间,线段最短 D. 经过一点有无数条直线
3. 如图,将下面的平面图形绕直线 旋转一周,得到的立体图形是( D )
A. B. C. D.
4. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,在原正方体中,与“一”字所在面相对的面上的汉字是( C )
A. 亚 B. 洲 C. 体 D. 育
5. 杨老师到几何王国去散步,刚走到“角”的家门口,就听到 , , 在争论, 说:“我是 ,我应该最大!” 说:“我是 ,我应该最大!” 也不甘示弱:“我是 ,我应该和 一样大!”请你判断一下 , , 谁最大( B )
A. 最大 B. 最大 C. 最大 D. 与 一样大
6. 如图所示的六角螺栓,从上面看得到的平面图形是( A )
A. B. C. D.
7. 如图是一张边长为 的正方形纸片,将其四个角都剪去一个边长为 的正方形,沿虚线折成一个无盖的长方体盒子,这个盒子的体积(单位: )为( D )
A. B. C. D.
8. 把一副三角尺 与 按如图所示方式拼在一起,已知 , ,其中 , , 三点在同一条直线上, 为 的平分线, 为 的平分线,则 的度数是( C )
A. B. C. D.
9. 如图,把一根绳子对折后用线段 表示,从点 处把绳子剪断,已知 ,若剪断后的各段绳子中最长的一段为 ,则绳子原来的长度为( B )
A. B. 或 C. D. 或
10. 已知线段 ,点 是直线 上一点,直线上共有3条线段: , 和 .若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段 的“巧分点”,线段 的“巧分点”的个数是 ( D )
A. 3 B. 6 C. 8 D. 9
二、填空题(每小题3分,共15分)
11. 已知 ,则它的余角为 .
12. 《雨不绝》是唐代诗人杜甫的作品,其中有诗句:“鸣雨既过渐细微,映空摇飏如丝飞.”译文:喧哗的雨已经过去,逐渐变得细微,映着天空摇漾的是如丝的细雨飘飞.诗中描写雨滴滴下来形成雨丝,用数学知识解释为点动成线.
13. [教材P140第12题变式]如图,某海域有三个小岛 , , ,在小岛 处观测到小岛 在它的北偏西 方向上,小岛 在它的南偏西 方向上,则 的度数是 .
第13题图
14. 如图是从不同方向看一个由若干个相同的小正方体组成的立体图形得到的图形,则组成这个立体图形的小正方体的个数为5.
第14题图
15. 有公共端点 的两条线段 , 组成一条折线 ,若该折线 上一点 把这条折线分成相等的两部分,我们把这个点 叫做这条折线的“折中点”.已知点 是折线 的“折中点”,点 为线段 的中点, , ,则线段 的长是8或32.
三、解答题(本大题共8个小题,共75分)
16. (8分)计算:
(1) ;
解:原式
.(4分)
(2) .
解:原式
.(4分)
17. (9分)如图是由一些大小相同的小正方体组合成的简单几何体,根据要求完成下列题目:
(1) 请在下面方格纸中分别画出从左面和从上面看到的平面图形(画出的图需涂上阴影).
解:如解图所示.(6分)
(2) 图中共有9(9分)个小正方体.
18. (9分)如图,已知 , , , 四点,根据下列要求画图:
(1) 作直线 ,射线 .
解:直线 ,射线 如解图所示.(4分)
(2) 在射线 上取一点 (点 在线段 上,且不与点 , 重合),画线段 .
解:线段 如解图所示.(6分)
(3) 延长线段 至点 ,使 .
解:如解图所示.(9分)
19. (9分)如图,已知 .
(1) 延长线段 至点 ,使 ,用尺规画出图形.
解:如解图1所示.(4分)
图1
(2) 若点 是线段 的中点,求线段 的长度.
解:因为 , ,所以 .
因为点 是线段 的中点,如解图2所示,则 .
图2
所以 .(9分)
20. (9分)如图,是小明家和学校所在地的简单地图,已知 , , ,点 为 的中点,回答下列问题:
(1) 图中到小明家距离相同的是哪些地方?
解:因为点 为 的中点,所以 .
因为 ,所以题图中到小明家距离相同的是学校和公园.(3分)
(2) 请用方向与距离描述学校、商场、停车场相对于小明家的位置.
解:由题图,可知学校在小明家北偏东 方向 处,商场在小明家北偏西 方向 处,停车场在小明家南偏东 方向 处.(9分)
21. (10分)已知 的补角等于它的余角的6倍.
(1) 求 的度数.
解:设 ,则它的余角为 ,它的补角为 .
根据题意,得 ,解得 .
所以 的度数为 .(4分)
(2) 如图,若 平分 , ,求 的度数.
解:因为 平分 ,所以 .
设 ,则 , .
因为 ,
所以 ,解得 .
所以 .(10分)
22. (10分)如图, 为线段 上一点, , , , 分别为 , 的中点.
(1) 若 ,求线段 的长.
解:因为 , 分别为 , 的中点,
所以 , .
所以 .
当 时, .(5分)
(2) 若 ,求线段 的长.
解:因为 , ,且 ,所以 .
因为 , 分别为 , 的中点,
所以 , .(8分)
所以 .(10分)
23. (11分)如图, 是线段 上任一点, , , 两点分别从 , 同时向 点运动,且 点的运动速度为 , 点的运动速度为 ,运动的时间为 .
(1) 若 .
① 运动 后, 的长为3(2分);
② 当 在线段 上运动时,试说明 .
解:因为 , ,所以 , .
所以 .
所以 .
所以 .(6分)
(2) 当 时,若 ,试探索 的长.
解:当 时, , .(7分)
分以下两种情况讨论:
①当点 在 的右边时,如解图1所示.
图1
由于 ,所以 .
所以 .
所以 .(9分)
②当点 在 的左边时,如解图2所示.
图2
,
所以 .
综上所述, 的长为 或 .(11分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1. 下列四个几何体中,含有曲面的是( )
A. B. C. D.
2. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是( )
A. 四边形周长小于三角形周长 B. 两点确定一条直线
C. 两点之间,线段最短 D. 经过一点有无数条直线
3. 如图,将下面的平面图形绕直线 旋转一周,得到的立体图形是( )
A. B. C. D.
4. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,在原正方体中,与“一”字所在面相对的面上的汉字是( )
A. 亚 B. 洲 C. 体 D. 育
5. 杨老师到几何王国去散步,刚走到“角”的家门口,就听到 , , 在争论, 说:“我是 ,我应该最大!” 说:“我是 ,我应该最大!” 也不甘示弱:“我是 ,我应该和 一样大!”请你判断一下 , , 谁最大( )
A. 最大 B. 最大 C. 最大 D. 与 一样大
6. 如图所示的六角螺栓,从上面看得到的平面图形是( )
A. B. C. D.
7. 如图是一张边长为 的正方形纸片,将其四个角都剪去一个边长为 的正方形,沿虚线折成一个无盖的长方体盒子,这个盒子的体积(单位: )为( )
A. B. C. D.
8. 把一副三角尺 与 按如图所示方式拼在一起,已知 , ,其中 , , 三点在同一条直线上, 为 的平分线, 为 的平分线,则 的度数是( )
A. B. C. D.
9. 如图,把一根绳子对折后用线段 表示,从点 处把绳子剪断,已知 ,若剪断后的各段绳子中最长的一段为 ,则绳子原来的长度为( )
A. B. 或 C. D. 或
10. 已知线段 ,点 是直线 上一点,直线上共有3条线段: , 和 .若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段 的“巧分点”,线段 的“巧分点”的个数是 ( )
A. 3 B. 6 C. 8 D. 9
二、填空题(每小题3分,共15分)
11. 已知 ,则它的余角为_________.
12. 《雨不绝》是唐代诗人杜甫的作品,其中有诗句:“鸣雨既过渐细微,映空摇飏如丝飞.”译文:喧哗的雨已经过去,逐渐变得细微,映着天空摇漾的是如丝的细雨飘飞.诗中描写雨滴滴下来形成雨丝,用数学知识解释为_________.
13. [教材P140第12题变式]如图,某海域有三个小岛 , , ,在小岛 处观测到小岛 在它的北偏西 方向上,小岛 在它的南偏西 方向上,则 的度数是_________.
第13题图
14. 如图是从不同方向看一个由若干个相同的小正方体组成的立体图形得到的图形,则组成这个立体图形的小正方体的个数为_________.
第14题图
15. 有公共端点 的两条线段 , 组成一条折线 ,若该折线 上一点 把这条折线分成相等的两部分,我们把这个点 叫做这条折线的“折中点”.已知点 是折线 的“折中点”,点 为线段 的中点, , ,则线段 的长是_________.
三、解答题(本大题共8个小题,共75分)
16. (8分)计算:
(1) ; (2) .
17. (9分)如图是由一些大小相同的小正方体组合成的简单几何体,根据要求完成下列题目:
(1) 请在下面方格纸中分别画出从左面和从上面看到的平面图形(画出的图需涂上阴影).
(2) 图中共有_________个小正方体.
18. (9分)如图,已知 , , , 四点,根据下列要求画图:
(1) 作直线 ,射线 .
(2) 在射线 上取一点 (点 在线段 上,且不与点 , 重合),画线段 .
(3) 延长线段 至点 ,使 .
19. (9分)如图,已知 .
(1) 延长线段 至点 ,使 ,用尺规画出图形.
(2) 若点 是线段 的中点,求线段 的长度.
20. (9分)如图,是小明家和学校所在地的简单地图,已知 , , ,点 为 的中点,回答下列问题:
(1) 图中到小明家距离相同的是哪些地方?
(2) 请用方向与距离描述学校、商场、停车场相对于小明家的位置.
21. (10分)已知 的补角等于它的余角的6倍.
(1) 求 的度数.
(2) 如图,若 平分 , ,求 的度数.
22. (10分)如图, 为线段 上一点, , , , 分别为 , 的中点.
(1) 若 ,求线段 的长.
(2) 若 ,求线段 的长.
23. (11分)如图, 是线段 上任一点, , , 两点分别从 , 同时向 点运动,且 点的运动速度为 , 点的运动速度为 ,运动的时间为 .
(1) 若 .
① 运动 后, 的长为_________;② 当 在线段 上运动时,试说明 .
(2) 当 时,若 ,试探索 的长.
参考答案
第四章 几何初步图形 单元测试题 2023-2024学年人教版七年级数学上册
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1. 下列四个几何体中,含有曲面的是( A )
A. B.
C. D.
2. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是( C )
A. 四边形周长小于三角形周长 B. 两点确定一条直线
C. 两点之间,线段最短 D. 经过一点有无数条直线
3. 如图,将下面的平面图形绕直线 旋转一周,得到的立体图形是( D )
A. B. C. D.
4. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,在原正方体中,与“一”字所在面相对的面上的汉字是( C )
A. 亚 B. 洲 C. 体 D. 育
5. 杨老师到几何王国去散步,刚走到“角”的家门口,就听到 , , 在争论, 说:“我是 ,我应该最大!” 说:“我是 ,我应该最大!” 也不甘示弱:“我是 ,我应该和 一样大!”请你判断一下 , , 谁最大( B )
A. 最大 B. 最大 C. 最大 D. 与 一样大
6. 如图所示的六角螺栓,从上面看得到的平面图形是( A )
A. B. C. D.
7. 如图是一张边长为 的正方形纸片,将其四个角都剪去一个边长为 的正方形,沿虚线折成一个无盖的长方体盒子,这个盒子的体积(单位: )为( D )
A. B. C. D.
8. 把一副三角尺 与 按如图所示方式拼在一起,已知 , ,其中 , , 三点在同一条直线上, 为 的平分线, 为 的平分线,则 的度数是( C )
A. B. C. D.
9. 如图,把一根绳子对折后用线段 表示,从点 处把绳子剪断,已知 ,若剪断后的各段绳子中最长的一段为 ,则绳子原来的长度为( B )
A. B. 或 C. D. 或
10. 已知线段 ,点 是直线 上一点,直线上共有3条线段: , 和 .若其中有一条线段的长度是另一条线段长度的两倍,则称点 是线段 的“巧分点”,线段 的“巧分点”的个数是 ( D )
A. 3 B. 6 C. 8 D. 9
二、填空题(每小题3分,共15分)
11. 已知 ,则它的余角为 .
12. 《雨不绝》是唐代诗人杜甫的作品,其中有诗句:“鸣雨既过渐细微,映空摇飏如丝飞.”译文:喧哗的雨已经过去,逐渐变得细微,映着天空摇漾的是如丝的细雨飘飞.诗中描写雨滴滴下来形成雨丝,用数学知识解释为点动成线.
13. [教材P140第12题变式]如图,某海域有三个小岛 , , ,在小岛 处观测到小岛 在它的北偏西 方向上,小岛 在它的南偏西 方向上,则 的度数是 .
第13题图
14. 如图是从不同方向看一个由若干个相同的小正方体组成的立体图形得到的图形,则组成这个立体图形的小正方体的个数为5.
第14题图
15. 有公共端点 的两条线段 , 组成一条折线 ,若该折线 上一点 把这条折线分成相等的两部分,我们把这个点 叫做这条折线的“折中点”.已知点 是折线 的“折中点”,点 为线段 的中点, , ,则线段 的长是8或32.
三、解答题(本大题共8个小题,共75分)
16. (8分)计算:
(1) ;
解:原式
.(4分)
(2) .
解:原式
.(4分)
17. (9分)如图是由一些大小相同的小正方体组合成的简单几何体,根据要求完成下列题目:
(1) 请在下面方格纸中分别画出从左面和从上面看到的平面图形(画出的图需涂上阴影).
解:如解图所示.(6分)
(2) 图中共有9(9分)个小正方体.
18. (9分)如图,已知 , , , 四点,根据下列要求画图:
(1) 作直线 ,射线 .
解:直线 ,射线 如解图所示.(4分)
(2) 在射线 上取一点 (点 在线段 上,且不与点 , 重合),画线段 .
解:线段 如解图所示.(6分)
(3) 延长线段 至点 ,使 .
解:如解图所示.(9分)
19. (9分)如图,已知 .
(1) 延长线段 至点 ,使 ,用尺规画出图形.
解:如解图1所示.(4分)
图1
(2) 若点 是线段 的中点,求线段 的长度.
解:因为 , ,所以 .
因为点 是线段 的中点,如解图2所示,则 .
图2
所以 .(9分)
20. (9分)如图,是小明家和学校所在地的简单地图,已知 , , ,点 为 的中点,回答下列问题:
(1) 图中到小明家距离相同的是哪些地方?
解:因为点 为 的中点,所以 .
因为 ,所以题图中到小明家距离相同的是学校和公园.(3分)
(2) 请用方向与距离描述学校、商场、停车场相对于小明家的位置.
解:由题图,可知学校在小明家北偏东 方向 处,商场在小明家北偏西 方向 处,停车场在小明家南偏东 方向 处.(9分)
21. (10分)已知 的补角等于它的余角的6倍.
(1) 求 的度数.
解:设 ,则它的余角为 ,它的补角为 .
根据题意,得 ,解得 .
所以 的度数为 .(4分)
(2) 如图,若 平分 , ,求 的度数.
解:因为 平分 ,所以 .
设 ,则 , .
因为 ,
所以 ,解得 .
所以 .(10分)
22. (10分)如图, 为线段 上一点, , , , 分别为 , 的中点.
(1) 若 ,求线段 的长.
解:因为 , 分别为 , 的中点,
所以 , .
所以 .
当 时, .(5分)
(2) 若 ,求线段 的长.
解:因为 , ,且 ,所以 .
因为 , 分别为 , 的中点,
所以 , .(8分)
所以 .(10分)
23. (11分)如图, 是线段 上任一点, , , 两点分别从 , 同时向 点运动,且 点的运动速度为 , 点的运动速度为 ,运动的时间为 .
(1) 若 .
① 运动 后, 的长为3(2分);
② 当 在线段 上运动时,试说明 .
解:因为 , ,所以 , .
所以 .
所以 .
所以 .(6分)
(2) 当 时,若 ,试探索 的长.
解:当 时, , .(7分)
分以下两种情况讨论:
①当点 在 的右边时,如解图1所示.
图1
由于 ,所以 .
所以 .
所以 .(9分)
②当点 在 的左边时,如解图2所示.
图2
,
所以 .
综上所述, 的长为 或 .(11分)
