14.2.2 完全平方公式一课一练(含解析)
文档属性
| 名称 | 14.2.2 完全平方公式一课一练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 615.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-30 16:19:22 | ||
图片预览


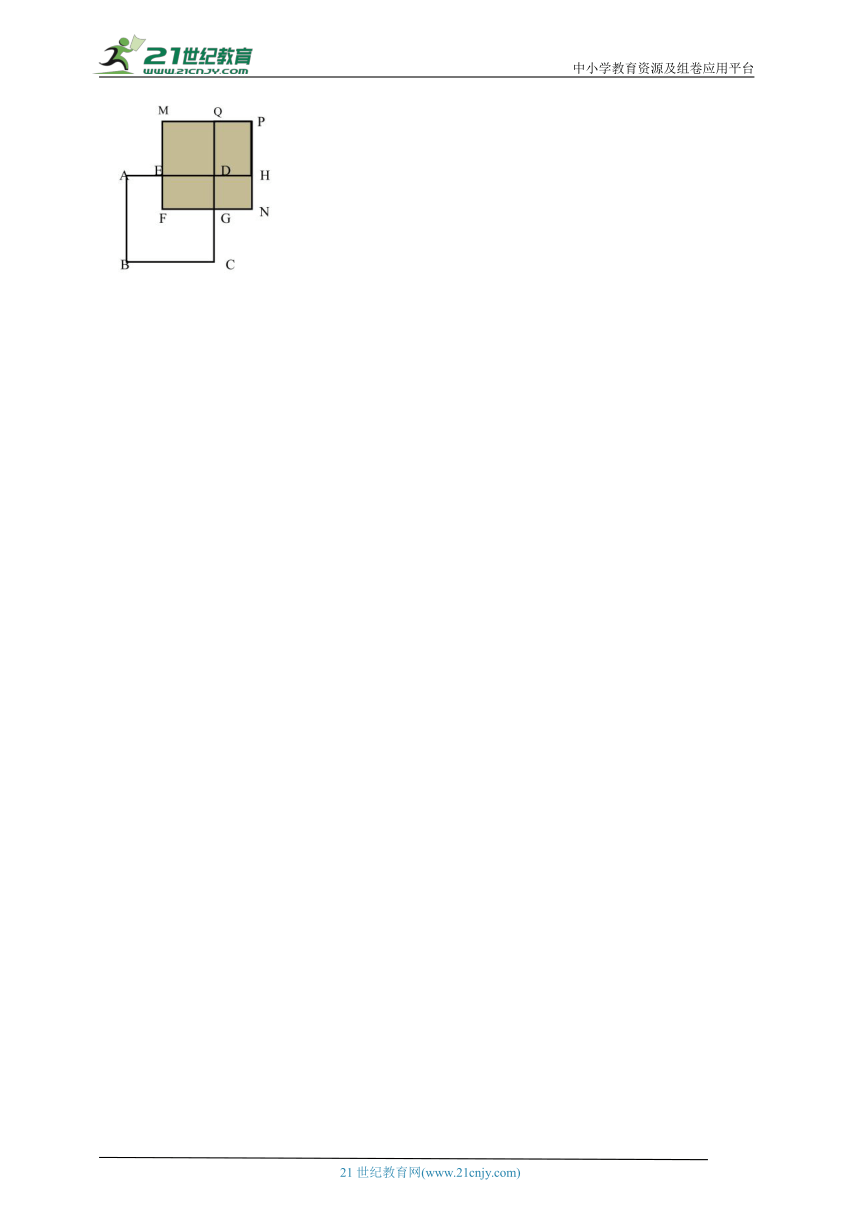
文档简介
中小学教育资源及组卷应用平台
14.2.2 完全平方公式一课一练
一、单选题
1.已知两个不等于0的实数 、 满足 ,则 等于( )
A.-2 B.-1 C.1 D.2
2.下列各式中,与 相等的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.下列各式的计算中,正确的是( )
A. B.
C. D.
5.已知,则的值是( ).
A.5 B.6 C.7 D.8
二、填空题
6.若a﹣b=7,ab=﹣12,则(a+b)2= .
三、计算题
7.计算:.
四、解答题
8.已知x= ﹣1,y=1+ ,求x2﹣xy+y2的值.
五、综合题
9.在学习“乘法公式“时,育红中学七(1)班数学兴趣小组在活动课上进行了这样的操作:作两条互相垂直的线段 和 ,把大正方形分成四部分(如图所示).
(1)观察发现
请用两种不同的方法表示图形的面积,得到一个等量关系:
(2)类比操作
请你作一个图形验证: .
(3)延伸运用
若 ,如图中阴影部分的面积和为13,求 的值.
六、实践探究题
10.【阅读理解】
“若x满足,求的值”
解:设,,则,,所以
【解决问题】
(1)若x满足,求的值.
(2)若x满足,求的值.
(3)如图,正方形ABCD的边长为x,,,长方形EFGD的面积是240,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
答案解析部分
1.【答案】A
【解析】【解答】解:∵ ,
∴ ,
∵两个不等于0的实数 、 满足 ,
∴ ,
故答案为:A.
【分析】将所求代数式通分并根据完全平方公式可得=,然后整体代换即可求解.
2.【答案】C
【解析】【解答】A: ,与 不相等,不符合题意;
B: ,与 不相等,不符合题意;
C: ,与 相等,符合题意;
D: ,与 不相等,不符合题意;
故答案为:C.
【分析】首先根据多项式乘以多项式的运算法则以及完全平方公式对各选项加以计算,然后进一步判断即可.
3.【答案】C
【解析】【解答】解: A:,计算错误;
B:,计算错误;
C:,计算正确;
D:,计算错误;
故答案为:C.
【分析】利用合并同类项法则,完全平方公式,同底数幂的乘法法则,积的乘方法则计算求解即可。
4.【答案】D
【解析】【解答】解:A. ,故不符合题意;
B. a2与a3不是同类项,不能合并,故不符合题意;
C. ,故不符合题意;
D. ,符合题意;
故答案为:D.
【分析】利用同底数幂的除法、合并同类项、完全平方公式及同底数幂的乘法逐项判定即可。
5.【答案】C
【解析】【解答】解:
故答案为:C.
【分析】给 左右两边同时平方即可求出的值 。
6.【答案】1
【解析】【解答】解:∵a﹣b=7,ab=﹣12,
∴(a+b)2
=(a﹣b)2+4ab
=72+4×(﹣12)
=1,
故答案为:1.
【分析】先根据完全平方公式进行变形,再整体代入求出即可.
7.【答案】解:原式
【解析】【分析】根据完全平方公式和多项式乘法进行计算即可。
8.【答案】解:
原式=
=
=
=6
【解析】【分析】先求出x-y的值,再运用完全平方公式进行因式分解得到x2﹣xy+y2=,再将x、y的值代入即可求解.
9.【答案】(1)
(2)只要画正确即可.
(3)由题意可知, , ,
.
,
,
.
【解析】【解答】(1)
【分析】(1)第一种方法为:大正方形面积=边长的平方,第二种表示方法为:两个小正方形的面积+两个长方形的面积.
(2)根据多项式画出图形,即可解答.
(3)由题意可知, , ,将 化简得 ,两边同时平方,将 代入计算即可.
10.【答案】(1)解:设,,则,,
∴;
(2)解:设,,则,,,,
∴.
(3)解:∵正方形ABCD的边长为x,,,
∴,,
∴,
设,,
∴,,
∴,
∴阴影部分的面积为:.
【解析】【分析】(1)设,,则,,再利用完全平方公式可得答案;
(2)参照题干中的计算方法求解即可;
(3)设,,则,,再求出阴影部分的面积即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
14.2.2 完全平方公式一课一练
一、单选题
1.已知两个不等于0的实数 、 满足 ,则 等于( )
A.-2 B.-1 C.1 D.2
2.下列各式中,与 相等的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.下列各式的计算中,正确的是( )
A. B.
C. D.
5.已知,则的值是( ).
A.5 B.6 C.7 D.8
二、填空题
6.若a﹣b=7,ab=﹣12,则(a+b)2= .
三、计算题
7.计算:.
四、解答题
8.已知x= ﹣1,y=1+ ,求x2﹣xy+y2的值.
五、综合题
9.在学习“乘法公式“时,育红中学七(1)班数学兴趣小组在活动课上进行了这样的操作:作两条互相垂直的线段 和 ,把大正方形分成四部分(如图所示).
(1)观察发现
请用两种不同的方法表示图形的面积,得到一个等量关系:
(2)类比操作
请你作一个图形验证: .
(3)延伸运用
若 ,如图中阴影部分的面积和为13,求 的值.
六、实践探究题
10.【阅读理解】
“若x满足,求的值”
解:设,,则,,所以
【解决问题】
(1)若x满足,求的值.
(2)若x满足,求的值.
(3)如图,正方形ABCD的边长为x,,,长方形EFGD的面积是240,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
答案解析部分
1.【答案】A
【解析】【解答】解:∵ ,
∴ ,
∵两个不等于0的实数 、 满足 ,
∴ ,
故答案为:A.
【分析】将所求代数式通分并根据完全平方公式可得=,然后整体代换即可求解.
2.【答案】C
【解析】【解答】A: ,与 不相等,不符合题意;
B: ,与 不相等,不符合题意;
C: ,与 相等,符合题意;
D: ,与 不相等,不符合题意;
故答案为:C.
【分析】首先根据多项式乘以多项式的运算法则以及完全平方公式对各选项加以计算,然后进一步判断即可.
3.【答案】C
【解析】【解答】解: A:,计算错误;
B:,计算错误;
C:,计算正确;
D:,计算错误;
故答案为:C.
【分析】利用合并同类项法则,完全平方公式,同底数幂的乘法法则,积的乘方法则计算求解即可。
4.【答案】D
【解析】【解答】解:A. ,故不符合题意;
B. a2与a3不是同类项,不能合并,故不符合题意;
C. ,故不符合题意;
D. ,符合题意;
故答案为:D.
【分析】利用同底数幂的除法、合并同类项、完全平方公式及同底数幂的乘法逐项判定即可。
5.【答案】C
【解析】【解答】解:
故答案为:C.
【分析】给 左右两边同时平方即可求出的值 。
6.【答案】1
【解析】【解答】解:∵a﹣b=7,ab=﹣12,
∴(a+b)2
=(a﹣b)2+4ab
=72+4×(﹣12)
=1,
故答案为:1.
【分析】先根据完全平方公式进行变形,再整体代入求出即可.
7.【答案】解:原式
【解析】【分析】根据完全平方公式和多项式乘法进行计算即可。
8.【答案】解:
原式=
=
=
=6
【解析】【分析】先求出x-y的值,再运用完全平方公式进行因式分解得到x2﹣xy+y2=,再将x、y的值代入即可求解.
9.【答案】(1)
(2)只要画正确即可.
(3)由题意可知, , ,
.
,
,
.
【解析】【解答】(1)
【分析】(1)第一种方法为:大正方形面积=边长的平方,第二种表示方法为:两个小正方形的面积+两个长方形的面积.
(2)根据多项式画出图形,即可解答.
(3)由题意可知, , ,将 化简得 ,两边同时平方,将 代入计算即可.
10.【答案】(1)解:设,,则,,
∴;
(2)解:设,,则,,,,
∴.
(3)解:∵正方形ABCD的边长为x,,,
∴,,
∴,
设,,
∴,,
∴,
∴阴影部分的面积为:.
【解析】【分析】(1)设,,则,,再利用完全平方公式可得答案;
(2)参照题干中的计算方法求解即可;
(3)设,,则,,再求出阴影部分的面积即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
