计算题特训:圆专项训练(含答案)数学六年级上册北师大版
文档属性
| 名称 | 计算题特训:圆专项训练(含答案)数学六年级上册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 10:02:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
计算题特训:圆(专项训练)数学六年级上册北师大版
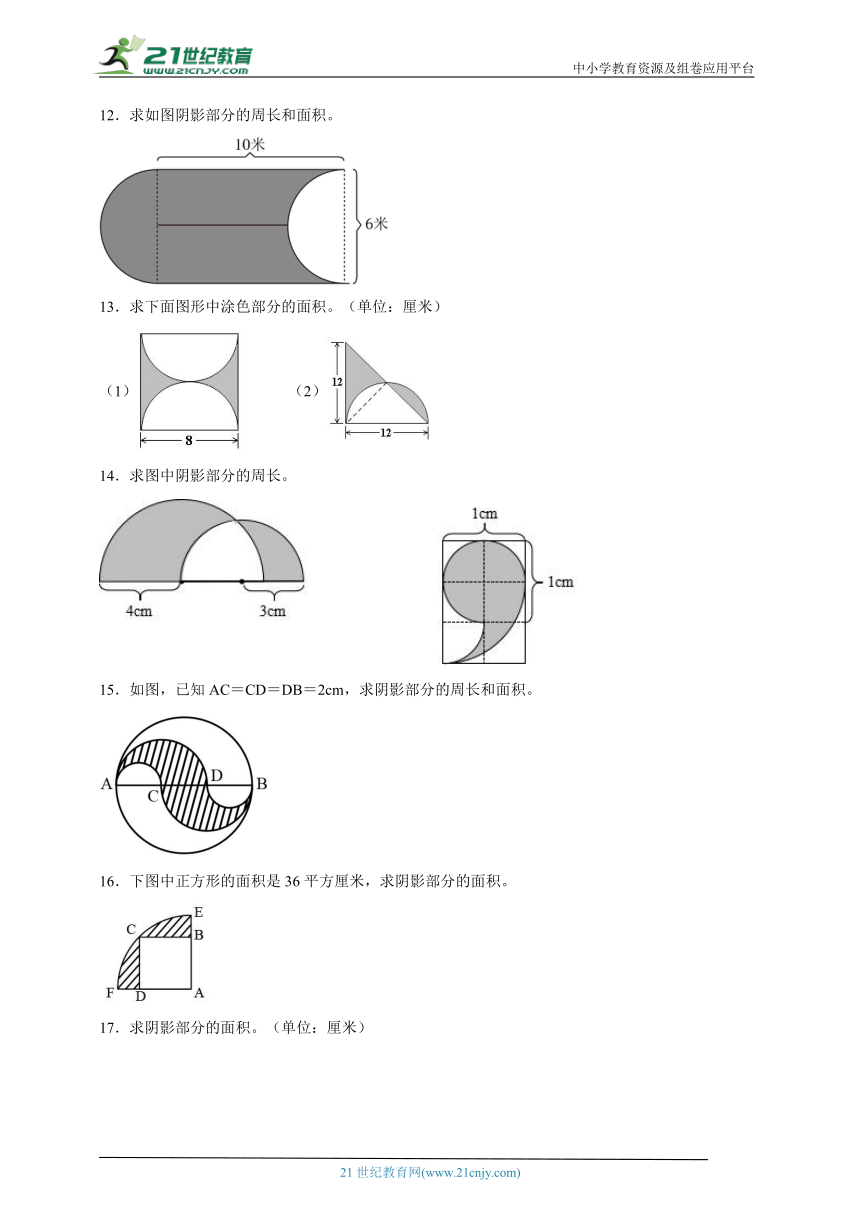
1.求下图中阴影部分的面积。
2.求阴影部分的面积.(单位:厘米)
3.计算下面图形的面积。
4.求下面各图阴影部分的面积。(单位:厘米)
5.求阴影部分的面积。(单位:)
6.求阴影部分的面积。
7.计算阴影部分的面积。(单位:cm)
8.求图中阴影部分的面积。
9.求阴影部分的面积(单位:厘米)
10.正方形的边长为10厘米(见图),按要求计算。
①求阴影部分周长。
②求空白部分面积。
11.计算如图图形的周长和面积。
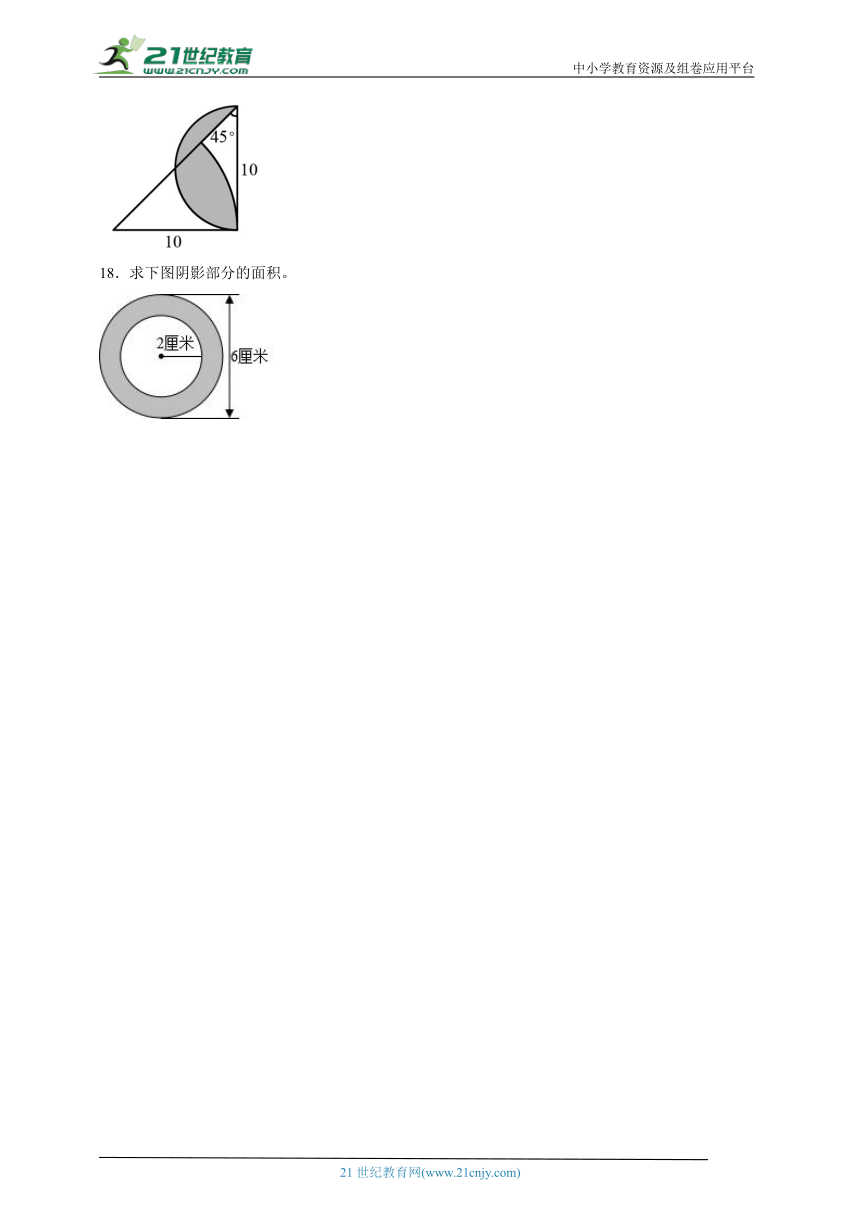
12.求如图阴影部分的周长和面积。
13.求下面图形中涂色部分的面积。(单位:厘米)
(1) (2)
14.求图中阴影部分的周长。
15.如图,已知AC=CD=DB=2cm,求阴影部分的周长和面积。
16.下图中正方形的面积是36平方厘米,求阴影部分的面积。
17.求阴影部分的面积。(单位:厘米)
18.求下图阴影部分的面积。
参考答案:
1.6.88cm2
【分析】根据图示,该阴影的面积等于长方形面积减去半圆面积;长方体面积公式:S=ab,圆的面积公式:S=πr2。
【详解】4×2×4-3.14×42÷2
=8×4-3.14×42÷2
=32-3.14×16÷2
=32-50.24÷2
=32-25.12
=6.88(cm2)
这个图形的面积是6.88 cm2。
2.3.72平方厘米
【详解】(4+6)×(4÷2)÷2-3.14×(4÷2)2÷2=3.72(平方厘米)
3.45.76平方厘米
【分析】观察图示可知,这个图形的面积=长为12厘米,宽为8厘米的长方形的面积-直径为8厘米的圆的面积,根据长方形面积=长×宽,圆的面积公式:S=πr ,代入数据求解即可。
【详解】12×8-3.14×(8÷2)2
=96-50.24
=45.76(平方厘米)
4.1.66平方厘米
【分析】观察此图,阴影部分的面积=梯形的面积-圆的面积。
【详解】(2+2.8)×2÷2-(2÷2)2×3.14
=4.8×2÷2-1×3.14
=4.8-3.14
=1.66(平方厘米)
5.25.12
【分析】由图可知,把上面的小半圆补到下面空白处,阴影部分正好是大圆的一半,其中大圆的半径是4cm,根据圆的面积公式,求出圆的面积乘 即可。
【详解】由题知:
。
6.30.375cm2
【分析】由图意可知,圆的半径是长方形的宽,图中阴影部分的面积等于长为10cm、宽为5cm的长方形的面积减去半径为5cm的圆的面积的;长方形的面积=长×宽,圆的面积=圆周率×半径的平方;据此计算。
【详解】5×10=50(平方厘米)
3.14×52×
=3.14×25×
=78.5×
=19.625(cm2)
50-19.625=30.375(cm2)
7.99.72cm2
【分析】阴影部分的面积=半圆的面积+长方形的面积,根据半圆的面积=πr2÷2;长方形的面积=长×宽;代入数据进行计算即可。
【详解】半圆的面积:
(12÷2)2×3.14÷2
=36×3.14÷2
=113.04÷2
=56.52(cm2)
长方形的面积:12×3.6=43.2(cm2)
阴影部分的面积:56.52+43.2=99.72(cm2)
8.6.88cm2
【分析】阴影部分的面积等于长方形面积减去半径是(8÷2)厘米半径的圆的面积。
【详解】圆的半径=长方形的宽=8÷2=4(cm)
8×4-3.14×42×
=32-3.14×16×
=32-3.14×8
=32-25.12
=6.88(cm2)
阴影部分的面积是6.88cm2。
9.48平方厘米
【分析】如图所示,将阴影①平移到空白②处,则阴影部分就成为一个梯形,利用梯形的面积公式即可求解。
【详解】据分析解答如下:
(6+10)×6÷2,
=16×6÷2,
=48(平方厘米);
答:阴影部分的面积是48平方厘米。
【点睛】解答此题的关键是:利用平移的方法,将阴影部分转化成一个梯形,问题即可得解。
10.①31.4厘米;
②21.5平方厘米
【分析】阴影部分的周长也就是圆的周长,圆的直径等于正方形的边长,圆的周长=,据此解答即可;
空白部分的面积等于正方形的面积减去圆的面积,正方形的面积=边长×边长,圆的面积=,据此解答即可。
【详解】①3.14×10=31.4(厘米)
答:阴影部分周长是31.4厘米。
②10÷2=5(厘米)
=78.5(平方厘米)
10×10=100(平方厘米)
100-78.5=21.5(平方厘米)
答:空白部分面积21.5平方厘米。
【点睛】考查圆的面积以及周长的相关知识,重点是能够熟记圆的周长与面积的计算公式。
11.35.7厘米;89.25平方厘米
【分析】通过观察可知本题的图形可以分成一个半圆形和一个长方形,计算周长时,计算出半径为5厘米的一个圆周长的一半,再加上长方形的一个长和两个宽,计算面积时,计算出一个半圆的面积再加上一个长方形的面积即可。
【详解】周长:3.14×2×5÷2+5×4
=15.7+20
=35.7(厘米)
面积:3.14×52÷2+2×5×5
=3.14×25÷2+2×5×5
=39.25+50
=89.25(平方厘米)
图形的周长为35.7厘米;面积为89.25平方厘米。
12.38.84米;60平方米
【分析】根据观察可知,左面阴影半圆和右面空白半圆是相同的,据此可知这个阴影部分的周长等于两条长为10米的线段与直径为6米的圆的周长的和,面积可根据长方形的面积公式:S=ab求出它的面积,据此解答。
【详解】10×2+3.14×6
=20+18.84
=38.84(米)
10×6=60(平方米)
所以,阴影部分的周长是38.84米,阴影部分的面积是60平方米。
13.(1)13.76平方厘米
(2)36平方厘米
【分析】(1)阴影部分的面积是正方形的面积减去一个圆的面积,圆的直径是8厘米,根据正方形的面积公式:边长×边长,圆的面积公式:S=πr2,把数代入即可求解。
(2)若把右侧的弓形涂色部分对称到左边,则把涂色部分通过转化拼接为一个小等腰直角三角形的面积;可先计算出以12为底和高的大等腰直角三角形的面积,再减去以12为斜边的空白小等腰直角三角形的面积,就是所求,根据三角形的面积公式:底×高÷2,把数代入即可求解。
【详解】(1)8×8-3.14×(8÷2)2
=64-3.14×42
=64-3.14×16
=64-50.24
=13.76(平方厘米)
所以阴影部分的面积是13.76平方厘米。
(2)12×12÷2-12×(12÷2)÷2
=72-12×6÷2
=72-36
=36(平方厘米)
阴影部分的面积是36平方厘米。
14.27.98cm;4.71cm
【分析】由图可知,阴影部分的周长=半径为4cm的半圆弧+半径为3cm的半圆弧+4+2,根据圆的周长=2r,代入即可求解;
由图可知,阴影部分周长=直径为1cm的圆的周长+半径为1cm的圆弧长度,根据圆的周长=2r=,代入即可求解。
【详解】2×3.14×4÷2+2×3.14×3÷2+4+3-(4-3)
=6.28×4÷2+6.28×3÷2+4+3-1
=25.12÷2+18.84÷2+4+3-1
=12.56+9.42+4+3-1
=21.98+4+3-1
=25.98+3-1
=28.98-1
=27.98(cm)
3.14×1+2×3.14×1÷4
=3.14+6.28÷4
=3.14+1.57
=4.71(cm)
15.周长18.84cm;面积9.42cm2
【分析】看图,以直线AB为界,将整个阴影部分一分为二,将下半部分向左翻转后,再和上半部分相接,可以得到完整的两个圆,其中外圆的半径是AD,内圆的直径是AC。由此易知,阴影部分的周长是这两个圆的周长之和,面积是这两个圆的面积之差。圆周长=2×3.14×半径=3.14×直径,圆面积=3.14×半径2,结合公式求出阴影部分的周长和面积即可。
【详解】周长:2×3.14×2+3.14×2
=12.56+6.28
=18.84(cm)
面积:3.14×22-3.14×(2÷2)2
=12.56-3.14
=9.42(cm2)
16.20.52平方厘米
【分析】如下图,连接A、C两点,可知AC=r,因为ABCD是正方形,所以三角形ABC的边AC的长度等于圆的半径、AC边上的高等于圆的半径的一半,设圆的半径是r,则三角形ABC的面积是:r×r÷2=r2,正方形ABCD的面积是r2,可以求出r2是多少,进而求出圆的面积;用圆的面积减去正方形的面积,即可求出阴影部分的面积。
【详解】如下图,连接A、C两点,设圆的半径是r,可得:
三角形ABC的面积是:
r×r÷2
=r2÷2
=r2
正方形ABCD的面积是
r2×2=r2
又:r2=36
所以,r2=72。
圆的面积是:
3.14×r2×-36
=3.14×72×-36
=226.08×-36
=56.52-36
=20.52(平方厘米)
所以,阴影部分的面积是20.52平方厘米。
【点睛】本题的关键是求出圆的半径的平方是多少,再进行解答。
17.28.5平方厘米
【分析】如下图,连接BD。阴影①和阴影②的面积和=以BC为直径的半圆面积-△BDC的面积;阴影③的面积=以AB为半径的圆面积的-△ABD的面积;用阴影①和阴影②的面积和加上阴影③的面积即可求出图中阴影部分的面积。因为△ABC是等腰直角三角形,所以△BDC和△ABD是完全一样的等腰直角三角形,即△BDC的面积和△ABD的面积相等,都等于△ABC面积的一半。
【详解】[3.14×(10÷2)2÷2-10×10÷2÷2]+[3.14×102×-10×10÷2÷2]
=[3.14×52÷2-100÷2÷2]+[3.14×100×-100÷2÷2]
=[3.14×25÷2-25]+[314×-25]
=[78.5÷2-25]+[39.25-25]
=[39.25-25]+[39.25-25]
=14.25+14.25
=28.5(平方厘米)
18.15.7平方厘米
【分析】观察图形可知,阴影部分的面积就是圆环的面积,根据圆环的面积公式:S=π(R2-r2),据此进行计算即可。
【详解】6÷2=3(厘米)
=3.14×(9-4)
=3.14×5
=15.7(平方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
计算题特训:圆(专项训练)数学六年级上册北师大版
1.求下图中阴影部分的面积。
2.求阴影部分的面积.(单位:厘米)
3.计算下面图形的面积。
4.求下面各图阴影部分的面积。(单位:厘米)
5.求阴影部分的面积。(单位:)
6.求阴影部分的面积。
7.计算阴影部分的面积。(单位:cm)
8.求图中阴影部分的面积。
9.求阴影部分的面积(单位:厘米)
10.正方形的边长为10厘米(见图),按要求计算。
①求阴影部分周长。
②求空白部分面积。
11.计算如图图形的周长和面积。
12.求如图阴影部分的周长和面积。
13.求下面图形中涂色部分的面积。(单位:厘米)
(1) (2)
14.求图中阴影部分的周长。
15.如图,已知AC=CD=DB=2cm,求阴影部分的周长和面积。
16.下图中正方形的面积是36平方厘米,求阴影部分的面积。
17.求阴影部分的面积。(单位:厘米)
18.求下图阴影部分的面积。
参考答案:
1.6.88cm2
【分析】根据图示,该阴影的面积等于长方形面积减去半圆面积;长方体面积公式:S=ab,圆的面积公式:S=πr2。
【详解】4×2×4-3.14×42÷2
=8×4-3.14×42÷2
=32-3.14×16÷2
=32-50.24÷2
=32-25.12
=6.88(cm2)
这个图形的面积是6.88 cm2。
2.3.72平方厘米
【详解】(4+6)×(4÷2)÷2-3.14×(4÷2)2÷2=3.72(平方厘米)
3.45.76平方厘米
【分析】观察图示可知,这个图形的面积=长为12厘米,宽为8厘米的长方形的面积-直径为8厘米的圆的面积,根据长方形面积=长×宽,圆的面积公式:S=πr ,代入数据求解即可。
【详解】12×8-3.14×(8÷2)2
=96-50.24
=45.76(平方厘米)
4.1.66平方厘米
【分析】观察此图,阴影部分的面积=梯形的面积-圆的面积。
【详解】(2+2.8)×2÷2-(2÷2)2×3.14
=4.8×2÷2-1×3.14
=4.8-3.14
=1.66(平方厘米)
5.25.12
【分析】由图可知,把上面的小半圆补到下面空白处,阴影部分正好是大圆的一半,其中大圆的半径是4cm,根据圆的面积公式,求出圆的面积乘 即可。
【详解】由题知:
。
6.30.375cm2
【分析】由图意可知,圆的半径是长方形的宽,图中阴影部分的面积等于长为10cm、宽为5cm的长方形的面积减去半径为5cm的圆的面积的;长方形的面积=长×宽,圆的面积=圆周率×半径的平方;据此计算。
【详解】5×10=50(平方厘米)
3.14×52×
=3.14×25×
=78.5×
=19.625(cm2)
50-19.625=30.375(cm2)
7.99.72cm2
【分析】阴影部分的面积=半圆的面积+长方形的面积,根据半圆的面积=πr2÷2;长方形的面积=长×宽;代入数据进行计算即可。
【详解】半圆的面积:
(12÷2)2×3.14÷2
=36×3.14÷2
=113.04÷2
=56.52(cm2)
长方形的面积:12×3.6=43.2(cm2)
阴影部分的面积:56.52+43.2=99.72(cm2)
8.6.88cm2
【分析】阴影部分的面积等于长方形面积减去半径是(8÷2)厘米半径的圆的面积。
【详解】圆的半径=长方形的宽=8÷2=4(cm)
8×4-3.14×42×
=32-3.14×16×
=32-3.14×8
=32-25.12
=6.88(cm2)
阴影部分的面积是6.88cm2。
9.48平方厘米
【分析】如图所示,将阴影①平移到空白②处,则阴影部分就成为一个梯形,利用梯形的面积公式即可求解。
【详解】据分析解答如下:
(6+10)×6÷2,
=16×6÷2,
=48(平方厘米);
答:阴影部分的面积是48平方厘米。
【点睛】解答此题的关键是:利用平移的方法,将阴影部分转化成一个梯形,问题即可得解。
10.①31.4厘米;
②21.5平方厘米
【分析】阴影部分的周长也就是圆的周长,圆的直径等于正方形的边长,圆的周长=,据此解答即可;
空白部分的面积等于正方形的面积减去圆的面积,正方形的面积=边长×边长,圆的面积=,据此解答即可。
【详解】①3.14×10=31.4(厘米)
答:阴影部分周长是31.4厘米。
②10÷2=5(厘米)
=78.5(平方厘米)
10×10=100(平方厘米)
100-78.5=21.5(平方厘米)
答:空白部分面积21.5平方厘米。
【点睛】考查圆的面积以及周长的相关知识,重点是能够熟记圆的周长与面积的计算公式。
11.35.7厘米;89.25平方厘米
【分析】通过观察可知本题的图形可以分成一个半圆形和一个长方形,计算周长时,计算出半径为5厘米的一个圆周长的一半,再加上长方形的一个长和两个宽,计算面积时,计算出一个半圆的面积再加上一个长方形的面积即可。
【详解】周长:3.14×2×5÷2+5×4
=15.7+20
=35.7(厘米)
面积:3.14×52÷2+2×5×5
=3.14×25÷2+2×5×5
=39.25+50
=89.25(平方厘米)
图形的周长为35.7厘米;面积为89.25平方厘米。
12.38.84米;60平方米
【分析】根据观察可知,左面阴影半圆和右面空白半圆是相同的,据此可知这个阴影部分的周长等于两条长为10米的线段与直径为6米的圆的周长的和,面积可根据长方形的面积公式:S=ab求出它的面积,据此解答。
【详解】10×2+3.14×6
=20+18.84
=38.84(米)
10×6=60(平方米)
所以,阴影部分的周长是38.84米,阴影部分的面积是60平方米。
13.(1)13.76平方厘米
(2)36平方厘米
【分析】(1)阴影部分的面积是正方形的面积减去一个圆的面积,圆的直径是8厘米,根据正方形的面积公式:边长×边长,圆的面积公式:S=πr2,把数代入即可求解。
(2)若把右侧的弓形涂色部分对称到左边,则把涂色部分通过转化拼接为一个小等腰直角三角形的面积;可先计算出以12为底和高的大等腰直角三角形的面积,再减去以12为斜边的空白小等腰直角三角形的面积,就是所求,根据三角形的面积公式:底×高÷2,把数代入即可求解。
【详解】(1)8×8-3.14×(8÷2)2
=64-3.14×42
=64-3.14×16
=64-50.24
=13.76(平方厘米)
所以阴影部分的面积是13.76平方厘米。
(2)12×12÷2-12×(12÷2)÷2
=72-12×6÷2
=72-36
=36(平方厘米)
阴影部分的面积是36平方厘米。
14.27.98cm;4.71cm
【分析】由图可知,阴影部分的周长=半径为4cm的半圆弧+半径为3cm的半圆弧+4+2,根据圆的周长=2r,代入即可求解;
由图可知,阴影部分周长=直径为1cm的圆的周长+半径为1cm的圆弧长度,根据圆的周长=2r=,代入即可求解。
【详解】2×3.14×4÷2+2×3.14×3÷2+4+3-(4-3)
=6.28×4÷2+6.28×3÷2+4+3-1
=25.12÷2+18.84÷2+4+3-1
=12.56+9.42+4+3-1
=21.98+4+3-1
=25.98+3-1
=28.98-1
=27.98(cm)
3.14×1+2×3.14×1÷4
=3.14+6.28÷4
=3.14+1.57
=4.71(cm)
15.周长18.84cm;面积9.42cm2
【分析】看图,以直线AB为界,将整个阴影部分一分为二,将下半部分向左翻转后,再和上半部分相接,可以得到完整的两个圆,其中外圆的半径是AD,内圆的直径是AC。由此易知,阴影部分的周长是这两个圆的周长之和,面积是这两个圆的面积之差。圆周长=2×3.14×半径=3.14×直径,圆面积=3.14×半径2,结合公式求出阴影部分的周长和面积即可。
【详解】周长:2×3.14×2+3.14×2
=12.56+6.28
=18.84(cm)
面积:3.14×22-3.14×(2÷2)2
=12.56-3.14
=9.42(cm2)
16.20.52平方厘米
【分析】如下图,连接A、C两点,可知AC=r,因为ABCD是正方形,所以三角形ABC的边AC的长度等于圆的半径、AC边上的高等于圆的半径的一半,设圆的半径是r,则三角形ABC的面积是:r×r÷2=r2,正方形ABCD的面积是r2,可以求出r2是多少,进而求出圆的面积;用圆的面积减去正方形的面积,即可求出阴影部分的面积。
【详解】如下图,连接A、C两点,设圆的半径是r,可得:
三角形ABC的面积是:
r×r÷2
=r2÷2
=r2
正方形ABCD的面积是
r2×2=r2
又:r2=36
所以,r2=72。
圆的面积是:
3.14×r2×-36
=3.14×72×-36
=226.08×-36
=56.52-36
=20.52(平方厘米)
所以,阴影部分的面积是20.52平方厘米。
【点睛】本题的关键是求出圆的半径的平方是多少,再进行解答。
17.28.5平方厘米
【分析】如下图,连接BD。阴影①和阴影②的面积和=以BC为直径的半圆面积-△BDC的面积;阴影③的面积=以AB为半径的圆面积的-△ABD的面积;用阴影①和阴影②的面积和加上阴影③的面积即可求出图中阴影部分的面积。因为△ABC是等腰直角三角形,所以△BDC和△ABD是完全一样的等腰直角三角形,即△BDC的面积和△ABD的面积相等,都等于△ABC面积的一半。
【详解】[3.14×(10÷2)2÷2-10×10÷2÷2]+[3.14×102×-10×10÷2÷2]
=[3.14×52÷2-100÷2÷2]+[3.14×100×-100÷2÷2]
=[3.14×25÷2-25]+[314×-25]
=[78.5÷2-25]+[39.25-25]
=[39.25-25]+[39.25-25]
=14.25+14.25
=28.5(平方厘米)
18.15.7平方厘米
【分析】观察图形可知,阴影部分的面积就是圆环的面积,根据圆环的面积公式:S=π(R2-r2),据此进行计算即可。
【详解】6÷2=3(厘米)
=3.14×(9-4)
=3.14×5
=15.7(平方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
