24.1 圆的有关性质(第3课时)
文档属性
| 名称 | 24.1 圆的有关性质(第3课时) |  | |
| 格式 | zip | ||
| 文件大小 | 607.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-16 10:48:40 | ||
图片预览

文档简介
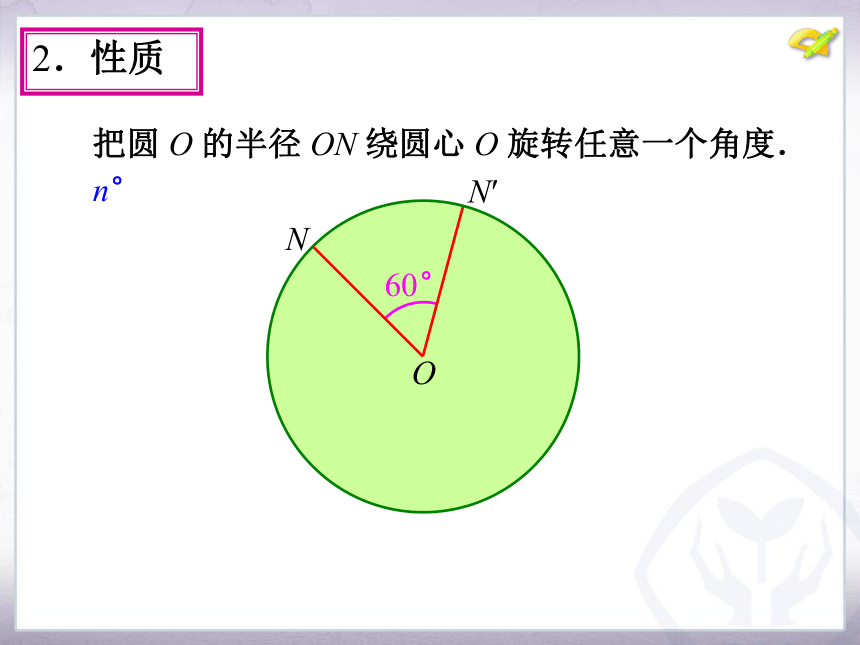
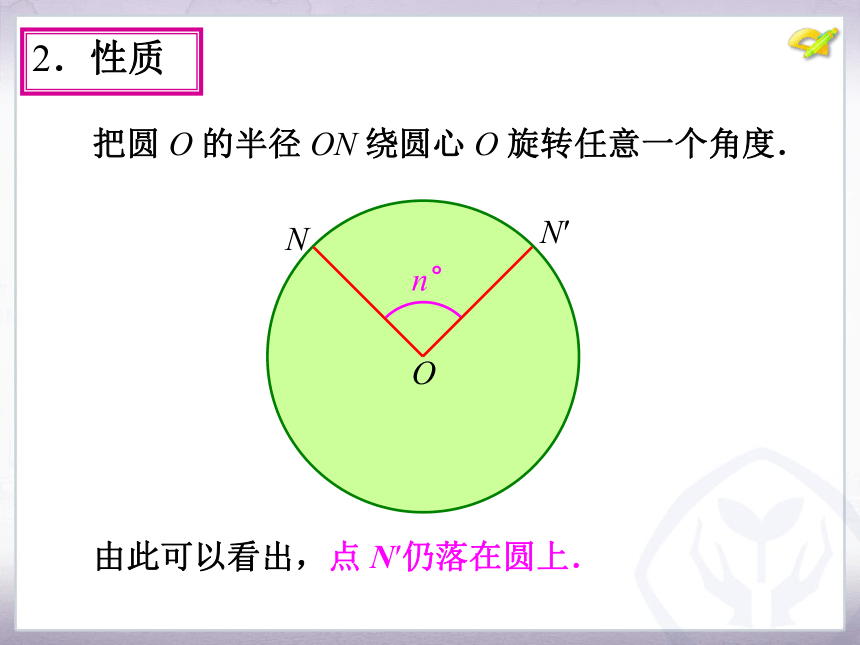
课件16张PPT。24.1 圆的有关性质(第3课时)九年级 上册1.思考 前面我们学习了圆是特殊的图形,圆是轴对称图形吗?它的对称轴是什么?那么,圆是中心对称图形吗?它的对称中心在哪里?·圆是中心对称图形,它的对称中心是圆心,N 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度. 15°O2.性质 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.NO15°N′ 30°2.性质 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.NO30°N′ 60°2.性质 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.NO60°N′ n°2.性质 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.NOn°N′ 由此可以看出,点 N′仍落在圆上.2.性质 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.2.性质NOn°N′ 性质:把圆绕圆心旋转任意一个角度后,仍与原来
的圆重合.(圆具有旋转不变性) 把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度.2.性质NOn°N′ 我们把顶点在圆心的角叫做圆心角.如∠NON′是
圆 O 的一个圆心角.3.探究 如图, 在⊙O 中,当圆心角∠AOB =∠A ` OB` 时,
它们所对的弧AB和弧A`B`、弦AB和弦A`B` 相等吗?为什么? 同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______ , 所对的弦______;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的弧______. 这样,我们就得到下面的定理: 在同圆或等圆中,相等的圆心角所对的弧相等,所 对的弦也相等. 相等相等相等相等4.定理 你能用几何符号表示出定理吗? 因为 AB=CD,所以∠AOB=∠COD.
又因为 AO=CO,BO=DO,
所以 △AOB ≌ △COD.
又因为 OE 、OF 是 AB 与 CD 对应边上的高,
所以 OE=OF.5.巩固练习∠AOB=∠CODAB=CD∠AOB=∠CODAB=CD相等.6.例题 例2 如图,AB 是⊙O 的直径, = = , ∠COD=35°,求∠AOE 的度数.6.例题 (1)本节课学习了哪些内容?
(2)圆心角、弧、弦之间有哪些关系?7.课堂小结 教科书习题 24.1 第 3,4 题.8.布置作业
它们所对的弧AB和弧A`B`、弦AB和弦A`B` 相等吗?为什么? 同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______ , 所对的弦______;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的弧______. 这样,我们就得到下面的定理: 在同圆或等圆中,相等的圆心角所对的弧相等,所 对的弦也相等. 相等相等相等相等4.定理 你能用几何符号表示出定理吗? 因为 AB=CD,所以∠AOB=∠COD.
又因为 AO=CO,BO=DO,
所以 △AOB ≌ △COD.
又因为 OE 、OF 是 AB 与 CD 对应边上的高,
所以 OE=OF.5.巩固练习∠AOB=∠CODAB=CD∠AOB=∠CODAB=CD相等.6.例题 例2 如图,AB 是⊙O 的直径, = = , ∠COD=35°,求∠AOE 的度数.6.例题 (1)本节课学习了哪些内容?
(2)圆心角、弧、弦之间有哪些关系?7.课堂小结 教科书习题 24.1 第 3,4 题.8.布置作业
同课章节目录
