5.1.2垂线(1)
图片预览



文档简介
(共24张PPT)
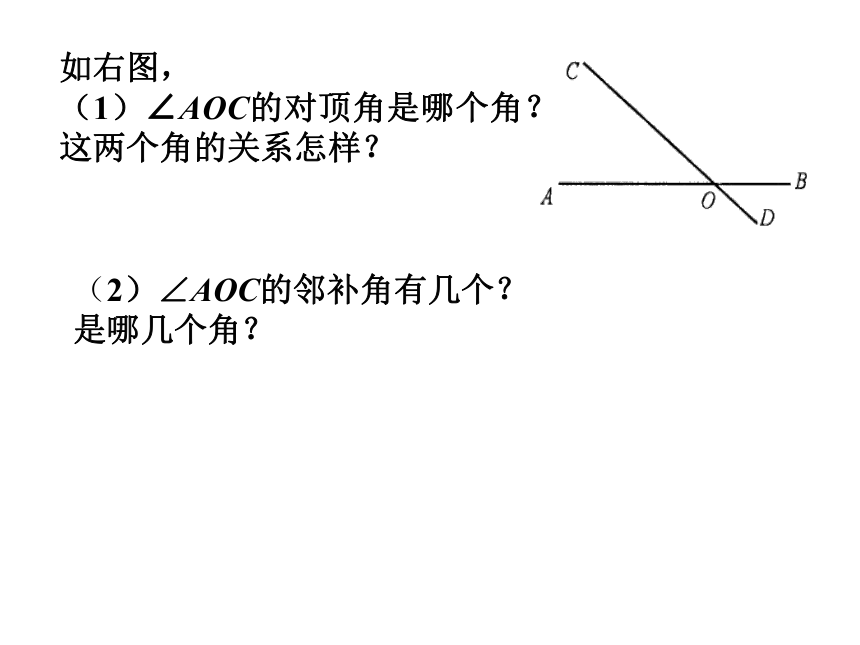
如右图,
(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的邻补角有几个?是哪几个角?
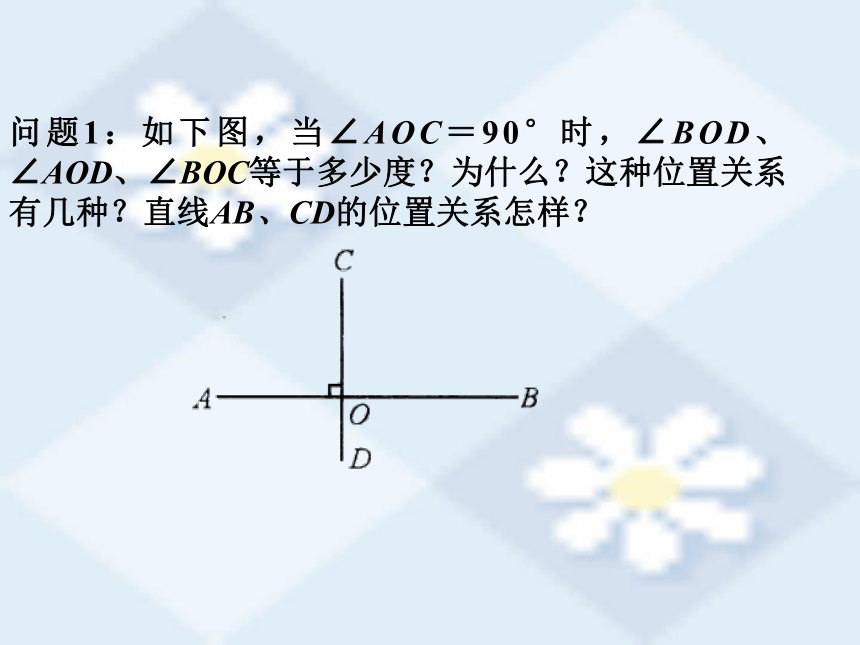
问题1:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?这种位置关系有几种?直线AB、CD的位置关系怎样?
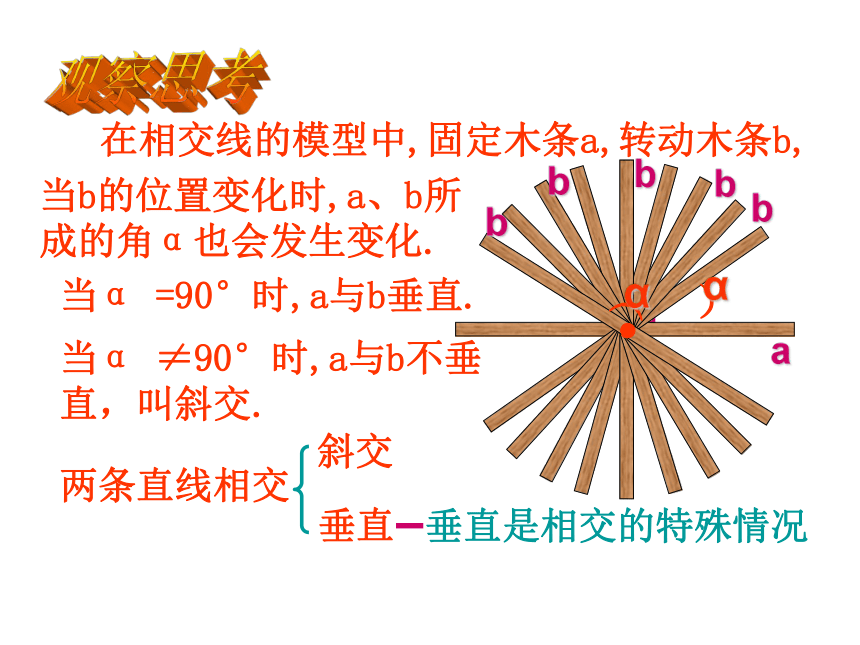
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
我国跳水运动员---田亮
1995年世界杯双人、团体、混合团体冠军; 1998年第13届亚运会男子10米跳台冠军; 1999年世界杯10米跳台男子单人、双人冠军; 1999年跳水大奖赛总决赛男子10米跳台冠军; 2000年世界杯男子10米跳台单人、双人冠军; 2000年第27届奥运会男子10米跳台单人冠军。 2001年世锦赛男子10米跳台单人、双人冠军; 2001年九运会男子10米跳台冠军; 2002年全国跳水冠军赛男子10米跳台冠军; 2002年世界杯男子10米跳台单人、双人冠军; 2002年全国锦标赛男子10米跳台冠军。
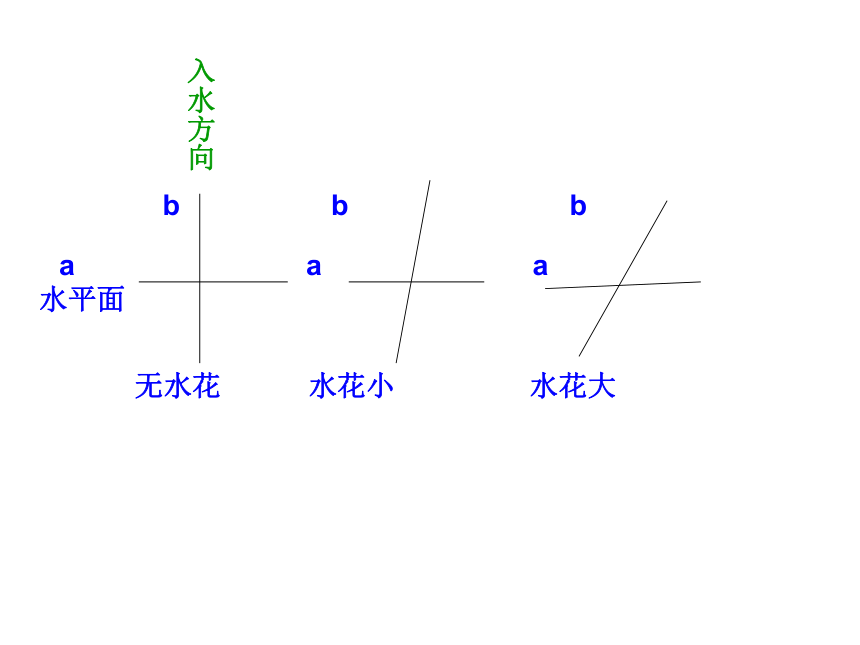
跳水运动员的入水姿势
b b b
a a a
水平面
无水花 水花小 水花大
入水方向
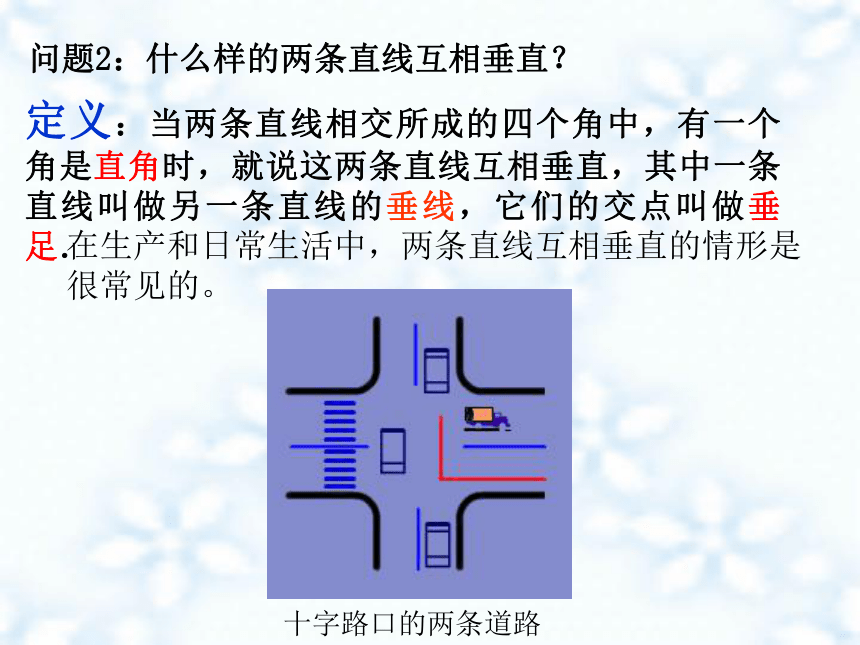
问题2:什么样的两条直线互相垂直?
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
在生产和日常生活中,两条直线互相垂直的情形是很常见的。
十字路口的两条道路
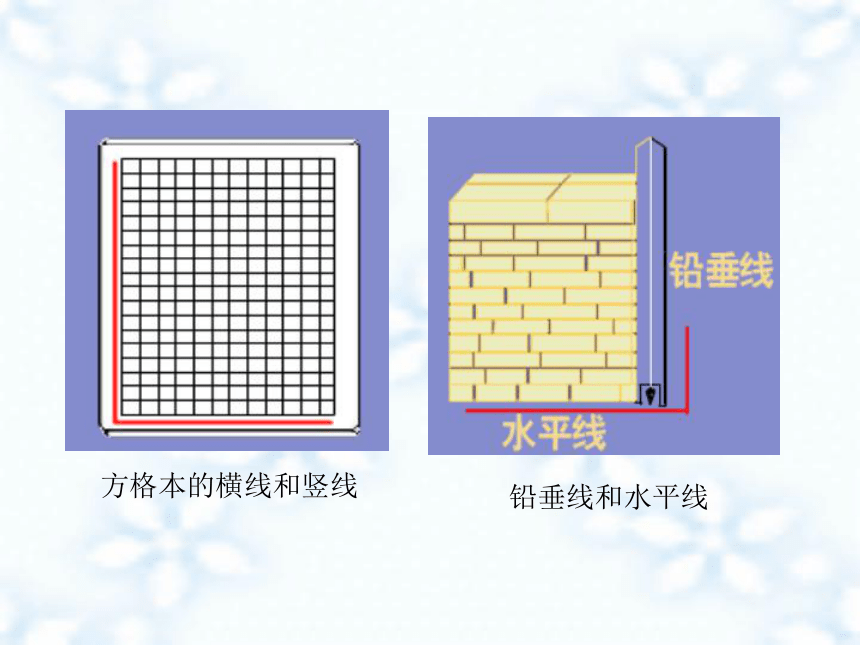
方格本的横线和竖线
铅垂线和水平线
垂直的记法、读法
直线AB、CD互相垂直,记作“AB⊥CD”或
“CD⊥AB”,读作“AB垂直于CD”,如果垂足为O,
记作“AB⊥CD,垂足为O”(如图).
垂直的定义的应用格式
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
C
D
O
A
B
选择题:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
(C)
2、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1
A
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
例1、如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35° ∠2=55°,则OE与AB的位置关系是
。
C
D
A
B
O
E
1
2
例2:如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36° (B) 64°
(C)144° (D) 54°
A
B
O
C
D
E
54°
想一想:
(1)直线a与直线b是互相垂直的两条直线,若直线a为已知直线,那么直线b的位置确定吗? 如何才能确定直线b的位置?
(2)通过画图,你能试着总结出什么结论?
结论1: 过直线上的一点有且只有一条直线与已知直线互相垂直。
结论2: 过直线外一点有且只有一条直线与已知
直线垂直.
结论: 过一点有且只有一条直线与已知直线垂直.
C
B
A
过直线外一点画出已知直线的垂线
C
B
A
D
一贴
二靠
1.贴住 已知 直线
2. 靠住 已知点
画法:
3.画垂线 标垂足
三画
结论:则直线DA即为所求垂线。
练习:
在图中,过点A分别作BD和DE的垂线.
D
A
B
E
D
A
B
E
D
A
B
E
N
M
结论:直线AM,AN为所求垂线。
变式:过A点作线段AN⊥DB,垂足为N
练习:
按要求画图:
A
B
C
A
B
C
A
B
C
D
F
D
E
F
E
(1)过B点作AC的垂线; (2)过A点作BC的垂线; (3)过C点作AB的垂线。
F
结论:略。
课堂练习
1.选择题
过点 向线段 所在直线引垂线,正确的是( ).
A B C D
C
课堂练习:
2. 过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
3.过点P分别向角的两边作垂线
.P
.P
.P
.P
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
作业:1、作业本(2)P1
如右图,
(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的邻补角有几个?是哪几个角?
问题1:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?这种位置关系有几种?直线AB、CD的位置关系怎样?
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
我国跳水运动员---田亮
1995年世界杯双人、团体、混合团体冠军; 1998年第13届亚运会男子10米跳台冠军; 1999年世界杯10米跳台男子单人、双人冠军; 1999年跳水大奖赛总决赛男子10米跳台冠军; 2000年世界杯男子10米跳台单人、双人冠军; 2000年第27届奥运会男子10米跳台单人冠军。 2001年世锦赛男子10米跳台单人、双人冠军; 2001年九运会男子10米跳台冠军; 2002年全国跳水冠军赛男子10米跳台冠军; 2002年世界杯男子10米跳台单人、双人冠军; 2002年全国锦标赛男子10米跳台冠军。
跳水运动员的入水姿势
b b b
a a a
水平面
无水花 水花小 水花大
入水方向
问题2:什么样的两条直线互相垂直?
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
在生产和日常生活中,两条直线互相垂直的情形是很常见的。
十字路口的两条道路
方格本的横线和竖线
铅垂线和水平线
垂直的记法、读法
直线AB、CD互相垂直,记作“AB⊥CD”或
“CD⊥AB”,读作“AB垂直于CD”,如果垂足为O,
记作“AB⊥CD,垂足为O”(如图).
垂直的定义的应用格式
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
C
D
O
A
B
选择题:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
(C)
2、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1
A
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
例1、如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35° ∠2=55°,则OE与AB的位置关系是
。
C
D
A
B
O
E
1
2
例2:如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36° (B) 64°
(C)144° (D) 54°
A
B
O
C
D
E
54°
想一想:
(1)直线a与直线b是互相垂直的两条直线,若直线a为已知直线,那么直线b的位置确定吗? 如何才能确定直线b的位置?
(2)通过画图,你能试着总结出什么结论?
结论1: 过直线上的一点有且只有一条直线与已知直线互相垂直。
结论2: 过直线外一点有且只有一条直线与已知
直线垂直.
结论: 过一点有且只有一条直线与已知直线垂直.
C
B
A
过直线外一点画出已知直线的垂线
C
B
A
D
一贴
二靠
1.贴住 已知 直线
2. 靠住 已知点
画法:
3.画垂线 标垂足
三画
结论:则直线DA即为所求垂线。
练习:
在图中,过点A分别作BD和DE的垂线.
D
A
B
E
D
A
B
E
D
A
B
E
N
M
结论:直线AM,AN为所求垂线。
变式:过A点作线段AN⊥DB,垂足为N
练习:
按要求画图:
A
B
C
A
B
C
A
B
C
D
F
D
E
F
E
(1)过B点作AC的垂线; (2)过A点作BC的垂线; (3)过C点作AB的垂线。
F
结论:略。
课堂练习
1.选择题
过点 向线段 所在直线引垂线,正确的是( ).
A B C D
C
课堂练习:
2. 过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
3.过点P分别向角的两边作垂线
.P
.P
.P
.P
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
作业:1、作业本(2)P1
