苏教版六年级下册数学几何综合(课件)(共28张PPT)
文档属性
| 名称 | 苏教版六年级下册数学几何综合(课件)(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 08:28:23 | ||
图片预览








文档简介
(共28张PPT)
小学数学 六年级
欢迎同学们
优翼
几何综合
1、公式法:基本图形的面积求解公式
2、概念法:根据基本图形的基本概念进行判断并求解
3、加减法: 相加求整,相减求部分。
4、分割法:将整体分割成若干个规则的多边形
5、割补法:将一部分割补到图形中的另一个地方组成较规则的图形进行求解。
6、等量代换法:如果图中有和所求部分面积相等的图形,可以通过先求该图形的面积间接求出所要求部分的面积。
7、重组法:将所求部分打乱重新组合。
8、倍比法:通过边长之间的倍数关系求解面积之间的倍数关系。
9、差不变法:A-B=(A+C)-(B+C)
10、整体法:在求解过程中没必要一定求出某一个具体的量,只需要知道某一个计算过程的整体也是可以求出面积的。
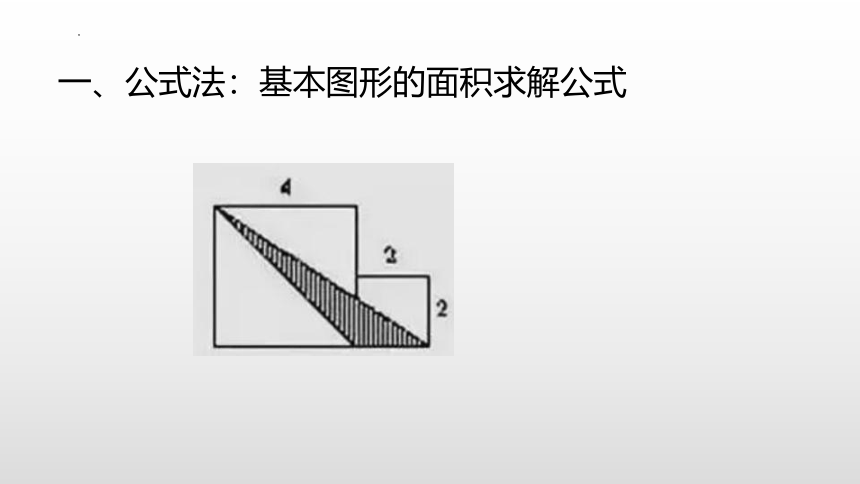
一、公式法:基本图形的面积求解公式
二、概念法:根据基本图形的基本概念进行判断并求解。
已知某平行四边形的长边和短边的长度分别是5厘米和3厘米,又知道以某一条边为底的高为4厘米,求平行四边形的面积。
三、加减法: 相加求整,相减求部分。
求解阴影部分的面积。(正方形的边长为4)
四、分割法:将整体分割成若干个规则的多边形
求解下面图形的面积。
五、割补法:将一部分割补到图形中的另一个地方组成较规则的图形进行求解。
求解阴影部分的面积。
六、等量代换法:如果图中有和所求部分面积相等的图形,可以通过先求该图形的面积间接求出所要求部分的面积。
如图所示,两个完全一样的三角形重叠放在一起,求图中阴影部分的面积。
七、将所求部分打乱重新组合。
八、倍比法:通过边长之间的倍数关系求解面积之间的倍数关系。
九、差不变法:A-B = (A+C)-(B+C)
图中大、小两个正方形边长分别是6厘米、4厘米,阴影部分的面积差是( )平方厘米。
十、整体法:在求解过程中没必要一定求出某一个具体的量,只需要知道某一个计算过程的整体也是可以求出面积的。
如图所示,正方形的边长正好等于圆的半径,已知正方形的面积是3,求圆形的面积。
练一练
【例题1】(50中)图中的长方形的长与宽的比为8:3,求阴影部分的面积。(单位:厘米)
阴影面积=半圆面积-长方形面积
3.14×20 ÷2=628(平方厘米)
20×2-4×2=32(厘米)
32÷8×3=12(厘米)
32×12=384(平方厘米)
628-384=244(平方厘米)
答:阴影部分的面积是244平方厘米。
练一练
【例题2】(38中)求下图中阴影部分的面积:(单位:厘米)
12.56-8=4.56(平方厘米)
割补法
答:阴影部分的面积是4.56平方厘米
3.14×4 ÷4=12.56(平方厘米)
4×4÷2=8(平方厘米)
练一练
【例题3】(48中)如图所示,AD=6cm,AB=4cm,DE=5cm,求甲比乙的面积多多少平方厘米?
4×6=24(平方厘米)
差不变法
答:甲比乙的面积多3平方厘米。
(5+4)×6÷2=27(平方厘米)
丙
27-24=3(平方厘米)
练一练
【例题4】(寿春)如图所示,平行四边形ABCD的边长BC为10厘米,直角三角形BCE的直角边EC为8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米,求EF的长。
平行四边形:40+10=50(平方厘米)
差不变法:
答:EF的长是3厘米。
三角形:8×10÷2=40(平方厘米)
50÷10=5(厘米)
8-5=3(厘米)
练一练
【例题5】(50中)如图所示,DE=4厘米,正方形ABCD的面积等于56厘米,求BF。
割补法
56÷4=14(厘米)
答:BF的长是14厘米。
练一练
【例题6】(46中)如图,正方形的边长是6厘米,求阴影部分的面积。
大墙角-小墙角=阴影面积
6×6-3.14×6×6÷4=7.74(平方厘米)
6÷2=3(厘米)
3×3-3.14×3×3÷4=1.935(平方厘米)
(7.74-1.935)×2=11.61(平方厘米)
答:阴影部分的面积是11.61平方厘米.
练一练
【例题7】(45中)已知四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为10厘米,那么图中阴影三角形BFD的面积为多少平方厘米?
等量代换
①+③=②+③ 所以 ①=②
10×10÷2=50(平方厘米)
答:阴影部分的面积是50平方厘米.
①
②
③
练一练
【例题8】(42中)如图,在△ABC中,AD是AC的三分之一,AE是AB的四分之一,若△AED的面积是2平方厘米,那么△ABC的面积是多少?
倍比法
2×3×4=24(平方厘米)
答:△ABC的面积是24平方厘米.
练一练
【例题9】(168联合)将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F,如果三角形ABC的面积等于1,那么三角形DEF的面积是多少?
倍比法
S△BCD=1cm2
S△DBE=1×(2+1)=3cm2
S△ABF=S△BDF=1×3=3cm2
S△CEF=(3+1)×2=8cm2
1+3+3+3+8=18cm2
练一练
【例10】(168联合)如图,平行四边的面积是20平方厘米,求阴影部分的面积。
狗牙模型
20÷2=10(平方厘米)
答:阴影部分的面积是10平方厘米.
练一练
【例题11】如图A与B是两个圆(只有四分之一)的圆心。那么,两个阴影部分的面积相差多少平方厘米?(单位:厘米)
差不变模型
②-①=(②+③)-(①+③)
答:两个阴影部分的面积相差1.42平方厘米。
③
3.14×4 ÷4=12.56cm2
3.14×2 ÷4=3.14cm2
12.56-3.14=9.42cm2
2×4=8cm2
9.42-8=1.42cm2
练一练
【例题12】(48中)如图,一个三角形的三个顶点分别为三个半径为3厘米的圆的圆心,则图中阴影部分的面积是多少?
答:两个阴影部分的面积相差14.13平方厘米。
3.14×3 ÷2=14.13cm2
阴影面积=半圆面积
逢3必过
游戏规则:
1、从第一个人开始报数,每出现3或3的倍数的学生喊过,S形轮流。
2、错误者重新报数。每个学生10个积分,错一个扣1分,扣光者表演才艺。
小学数学 六年级
欢迎同学们
优翼
几何综合
1、公式法:基本图形的面积求解公式
2、概念法:根据基本图形的基本概念进行判断并求解
3、加减法: 相加求整,相减求部分。
4、分割法:将整体分割成若干个规则的多边形
5、割补法:将一部分割补到图形中的另一个地方组成较规则的图形进行求解。
6、等量代换法:如果图中有和所求部分面积相等的图形,可以通过先求该图形的面积间接求出所要求部分的面积。
7、重组法:将所求部分打乱重新组合。
8、倍比法:通过边长之间的倍数关系求解面积之间的倍数关系。
9、差不变法:A-B=(A+C)-(B+C)
10、整体法:在求解过程中没必要一定求出某一个具体的量,只需要知道某一个计算过程的整体也是可以求出面积的。
一、公式法:基本图形的面积求解公式
二、概念法:根据基本图形的基本概念进行判断并求解。
已知某平行四边形的长边和短边的长度分别是5厘米和3厘米,又知道以某一条边为底的高为4厘米,求平行四边形的面积。
三、加减法: 相加求整,相减求部分。
求解阴影部分的面积。(正方形的边长为4)
四、分割法:将整体分割成若干个规则的多边形
求解下面图形的面积。
五、割补法:将一部分割补到图形中的另一个地方组成较规则的图形进行求解。
求解阴影部分的面积。
六、等量代换法:如果图中有和所求部分面积相等的图形,可以通过先求该图形的面积间接求出所要求部分的面积。
如图所示,两个完全一样的三角形重叠放在一起,求图中阴影部分的面积。
七、将所求部分打乱重新组合。
八、倍比法:通过边长之间的倍数关系求解面积之间的倍数关系。
九、差不变法:A-B = (A+C)-(B+C)
图中大、小两个正方形边长分别是6厘米、4厘米,阴影部分的面积差是( )平方厘米。
十、整体法:在求解过程中没必要一定求出某一个具体的量,只需要知道某一个计算过程的整体也是可以求出面积的。
如图所示,正方形的边长正好等于圆的半径,已知正方形的面积是3,求圆形的面积。
练一练
【例题1】(50中)图中的长方形的长与宽的比为8:3,求阴影部分的面积。(单位:厘米)
阴影面积=半圆面积-长方形面积
3.14×20 ÷2=628(平方厘米)
20×2-4×2=32(厘米)
32÷8×3=12(厘米)
32×12=384(平方厘米)
628-384=244(平方厘米)
答:阴影部分的面积是244平方厘米。
练一练
【例题2】(38中)求下图中阴影部分的面积:(单位:厘米)
12.56-8=4.56(平方厘米)
割补法
答:阴影部分的面积是4.56平方厘米
3.14×4 ÷4=12.56(平方厘米)
4×4÷2=8(平方厘米)
练一练
【例题3】(48中)如图所示,AD=6cm,AB=4cm,DE=5cm,求甲比乙的面积多多少平方厘米?
4×6=24(平方厘米)
差不变法
答:甲比乙的面积多3平方厘米。
(5+4)×6÷2=27(平方厘米)
丙
27-24=3(平方厘米)
练一练
【例题4】(寿春)如图所示,平行四边形ABCD的边长BC为10厘米,直角三角形BCE的直角边EC为8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米,求EF的长。
平行四边形:40+10=50(平方厘米)
差不变法:
答:EF的长是3厘米。
三角形:8×10÷2=40(平方厘米)
50÷10=5(厘米)
8-5=3(厘米)
练一练
【例题5】(50中)如图所示,DE=4厘米,正方形ABCD的面积等于56厘米,求BF。
割补法
56÷4=14(厘米)
答:BF的长是14厘米。
练一练
【例题6】(46中)如图,正方形的边长是6厘米,求阴影部分的面积。
大墙角-小墙角=阴影面积
6×6-3.14×6×6÷4=7.74(平方厘米)
6÷2=3(厘米)
3×3-3.14×3×3÷4=1.935(平方厘米)
(7.74-1.935)×2=11.61(平方厘米)
答:阴影部分的面积是11.61平方厘米.
练一练
【例题7】(45中)已知四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为10厘米,那么图中阴影三角形BFD的面积为多少平方厘米?
等量代换
①+③=②+③ 所以 ①=②
10×10÷2=50(平方厘米)
答:阴影部分的面积是50平方厘米.
①
②
③
练一练
【例题8】(42中)如图,在△ABC中,AD是AC的三分之一,AE是AB的四分之一,若△AED的面积是2平方厘米,那么△ABC的面积是多少?
倍比法
2×3×4=24(平方厘米)
答:△ABC的面积是24平方厘米.
练一练
【例题9】(168联合)将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F,如果三角形ABC的面积等于1,那么三角形DEF的面积是多少?
倍比法
S△BCD=1cm2
S△DBE=1×(2+1)=3cm2
S△ABF=S△BDF=1×3=3cm2
S△CEF=(3+1)×2=8cm2
1+3+3+3+8=18cm2
练一练
【例10】(168联合)如图,平行四边的面积是20平方厘米,求阴影部分的面积。
狗牙模型
20÷2=10(平方厘米)
答:阴影部分的面积是10平方厘米.
练一练
【例题11】如图A与B是两个圆(只有四分之一)的圆心。那么,两个阴影部分的面积相差多少平方厘米?(单位:厘米)
差不变模型
②-①=(②+③)-(①+③)
答:两个阴影部分的面积相差1.42平方厘米。
③
3.14×4 ÷4=12.56cm2
3.14×2 ÷4=3.14cm2
12.56-3.14=9.42cm2
2×4=8cm2
9.42-8=1.42cm2
练一练
【例题12】(48中)如图,一个三角形的三个顶点分别为三个半径为3厘米的圆的圆心,则图中阴影部分的面积是多少?
答:两个阴影部分的面积相差14.13平方厘米。
3.14×3 ÷2=14.13cm2
阴影面积=半圆面积
逢3必过
游戏规则:
1、从第一个人开始报数,每出现3或3的倍数的学生喊过,S形轮流。
2、错误者重新报数。每个学生10个积分,错一个扣1分,扣光者表演才艺。
