第2章轴对称图形 选择题专题训练(含解析)苏科版八年级数学上册
文档属性
| 名称 | 第2章轴对称图形 选择题专题训练(含解析)苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 467.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 15:37:08 | ||
图片预览




文档简介
2023-2024学年苏科版八年级数学上册《第2章轴对称图形》选择题专题训练
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.一个等腰三角形的两边长分别为3和5,则它的周长为( )
A.7 B.9 C.11或13 D.9或12
3.等腰三角形的一个角是,则它的底角是( )
A. B. C.和 D.和
4.如图,将一个长方形纸条折成如图的形状,若已知,则为( )
A. B. C. D.
5.如图,在中,,的中垂线交于点,交于点,连接,若,则的度数为( )
A. B. C. D.
6.如图,点在内部,平分,,连接若的面积为,则的面积为( )
A. B. C. D.
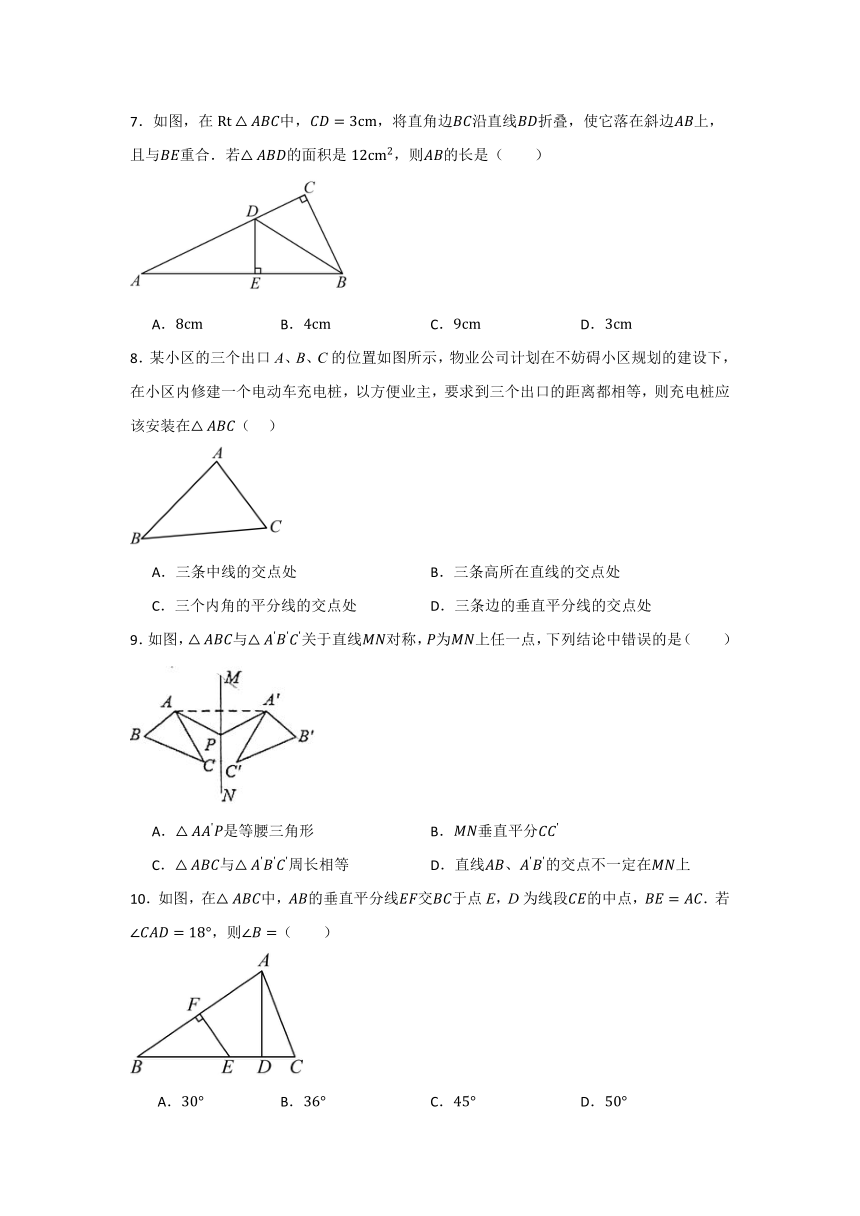
7.如图,在中,,将直角边沿直线折叠,使它落在斜边上,且与重合.若的面积是,则的长是( )
A. B. C. D.
8.某小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该安装在( )
A.三条中线的交点处 B.三条高所在直线的交点处
C.三个内角的平分线的交点处 D.三条边的垂直平分线的交点处
9.如图,与关于直线对称,为上任一点,下列结论中错误的是( )
A.是等腰三角形 B.垂直平分
C.与周长相等 D.直线、的交点不一定在上
10.如图,在中,的垂直平分线交于点E,D为线段的中点,.若,则( )
A. B. C. D.
11.如图,是中的平分线,交AB于点E,,交于点F.若,则的长是( )
A.4 B.3 C.6 D.5
12.如图,在中,,.的平分线与的垂直平分线交于点O,点E、F分别在边上,点C沿折叠后与点O重合,则的度数是( )
A. B. C. D.
13.如图,以正五边形的边为边作等边三角形,使点在其内部,连接,则的大小是( )
A. B. C. D.
14.如图,在中,的垂直平分线分别交、于点、,连接.若4,的周长为24,则的周长为( )
A.12 B.16 C.18 D.20
15.如图,为上一点,连接平分交于点,且,,,,则的长为( )
A.1.2 B.1.5 C.2 D.3
16.如图,在的正方形网格中,每个小正方形的顶点称为格点,点A,B均在格点上.要在格点上确定一点C,连接和,使是以为顶角的等腰三角形,则网格中满足条件的点C的个数是( )
A.3个 B.4个 C.5个 D.6个
17.如图,等腰直角三角形中,,是的中点,于点,交的延长线于点,若,则的面积为( )
A.40 B.46 C.48 D.50
18.已知:在等腰中,,垂足为点D,,则的度数有几种可能( )
A.6种 B.5种 C.4种 D.3种
19.已知,在内有一定点P,点M,N分别是,上的动点,若的周长最小值为3,则的长为( )
A. B.3 C. D.
20.如图,C为线段上一动点(不与点A,E重合),在同侧分别作正和正,与交于点O,与交于点P,与交于点Q,连接,以下五个结论:;;;;.一定成立的结论有( ).
A. B. C. D.
参考答案
1.解:A、图形不能找到一条直线,直线两旁的部分能够互相重合,不是轴对称图形,故此选项不符合题意;
B、图形不能找到一条直线,直线两旁的部分能够互相重合,不是轴对称图形,故此选项不符合题意;
C、图形不能找到一条直线,直线两旁的部分能够互相重合,不是轴对称图形,故此选项不符合题意;
D、图形能找到一条直线,使图形沿一条直线折叠,是轴对称图形,故此选项符合题意.
故选:D.
2.解:分如下两种情况:
①当腰为3,底为5,此时等腰三角形三边分别为3,3,5,且,故三角形存在,
因此它的周长为;
②当腰为5,底为3,此时等腰三角形三边分别为5,5,3,且,故三角形存在,
因此它的周长为;
综上所述,这个等腰三角形的周长为11或13,
故选:C.
3.解:①当是顶角时,底角,
②当是底角时,由三角形内角和定理可知,此种情况不存在,
它的底角是,
故选:A.
4.解:如图,∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故选:C.
5.解:∵为的垂直平分线,,
∴,,
∴,
∵,
∴,
∴.
故选:C.
6.解:延长交于,
平分,
,
,
,
,
,
,
的面积的面积,的面积的面积,
的面积的面积的面积的面积,
的面积的面积.
故选:B.
7.解:将直角边沿直线折叠,使它落在斜边上,且与重合,
,,
在和中,
,
,
,,
,
的面积是,
,
,
故选:A.
8.解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.
则充电桩应该安装在三条边的垂直平分线的交点处.
故选:D.
9.解:∵与关于直线对称,为上任一点,
又∵对称轴上的任何一点到两个对应点之间的距离相等,
∴,
∴是等腰三角形,选项A正确,不符合题意;
∵轴对称图形对应点所连的线段被对称轴垂直平分,
∴垂直平分,选项B正确,不符合题意;
∵轴对称图形对应的角、线段都相等,
∴与是全等三角形,周长也必然相等,选项C正确,不符合题意;
∵直线、关于直线对称,因此交点一定在上.
∴选项D错误,符合题意.
故选D.
10.解:连接,如图所示,
∵垂直平分,
∴,
∵,
∴,
∴是等腰三角形,
∵D为线段的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选:B;
11.解:∵是中的平分线,交AB于点E,,交AC于点F
∴.
又∵,
∴
解得.
故选:B.
12.解:连接,如下图:
∵
∴
∵平分
∴
又∵垂直平分
∴
∴
∴
∵平分,
∴垂直平分
∴
∴
由折叠的性质可得:,
∴
∴
故选:C
13.解:∵是等边三角形,正五边形的每个内角为,
∴,
∵,
∴.
故选:B.
14.解:∵是的垂直平分线,
∴,
∴,
∵的周长为24,则
∴
∴的周长为,
故选:B.
15.解: 平分,,
,,
,
,
,
,
故选:B.
16.解:如图所示.
网格中满足条件的点C有,共4个,
故选B.
17.解:,
,
,
,
,,,
.
在和中
,
,
.
,为中点,
.
,
,
,
,
的面积是.
故选:C.
18.解:分两种情况:(1)当为底角时,
①如图1,当时,
,
,
,
,
;
②如图2,当时,
,
,
,
;
③如图3,当时,
,,
,
,
;
(2)当为顶角时,
①如图4,,
,
,
,
,
;
②如图5,,
,
,
,
,
,
.
的度数为或或或或共5种.
故选:B.
19.解:作P关于的对称点D,作P关于的对称点E,连接交于M,交于N,连接,则此时的周长最小,
连接,
∵P、D关于对称,
∴,
同理,
∴,
∵P、D关于对称,
∴,
∵,
∴,
同理,
∴,
∵,
∴是等边三角形,
∴,
∵的周长是,
∴
故选:B.
20.解:①∵和是等边三角形,
∴,,,
∴,
在和中,
∴,
∴,,①正确;
②,
在和中,
∴,
∴,
∴,
∴,
∴,②正确;
③与②的过程同理得:,
∴,
③正确;
④∵,且,
∴,故④错误;
⑤∵,
∴,
∵是等边三角形,,
∴,
∴,
∴,
∴⑤正确.
故选:D
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.一个等腰三角形的两边长分别为3和5,则它的周长为( )
A.7 B.9 C.11或13 D.9或12
3.等腰三角形的一个角是,则它的底角是( )
A. B. C.和 D.和
4.如图,将一个长方形纸条折成如图的形状,若已知,则为( )
A. B. C. D.
5.如图,在中,,的中垂线交于点,交于点,连接,若,则的度数为( )
A. B. C. D.
6.如图,点在内部,平分,,连接若的面积为,则的面积为( )
A. B. C. D.
7.如图,在中,,将直角边沿直线折叠,使它落在斜边上,且与重合.若的面积是,则的长是( )
A. B. C. D.
8.某小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该安装在( )
A.三条中线的交点处 B.三条高所在直线的交点处
C.三个内角的平分线的交点处 D.三条边的垂直平分线的交点处
9.如图,与关于直线对称,为上任一点,下列结论中错误的是( )
A.是等腰三角形 B.垂直平分
C.与周长相等 D.直线、的交点不一定在上
10.如图,在中,的垂直平分线交于点E,D为线段的中点,.若,则( )
A. B. C. D.
11.如图,是中的平分线,交AB于点E,,交于点F.若,则的长是( )
A.4 B.3 C.6 D.5
12.如图,在中,,.的平分线与的垂直平分线交于点O,点E、F分别在边上,点C沿折叠后与点O重合,则的度数是( )
A. B. C. D.
13.如图,以正五边形的边为边作等边三角形,使点在其内部,连接,则的大小是( )
A. B. C. D.
14.如图,在中,的垂直平分线分别交、于点、,连接.若4,的周长为24,则的周长为( )
A.12 B.16 C.18 D.20
15.如图,为上一点,连接平分交于点,且,,,,则的长为( )
A.1.2 B.1.5 C.2 D.3
16.如图,在的正方形网格中,每个小正方形的顶点称为格点,点A,B均在格点上.要在格点上确定一点C,连接和,使是以为顶角的等腰三角形,则网格中满足条件的点C的个数是( )
A.3个 B.4个 C.5个 D.6个
17.如图,等腰直角三角形中,,是的中点,于点,交的延长线于点,若,则的面积为( )
A.40 B.46 C.48 D.50
18.已知:在等腰中,,垂足为点D,,则的度数有几种可能( )
A.6种 B.5种 C.4种 D.3种
19.已知,在内有一定点P,点M,N分别是,上的动点,若的周长最小值为3,则的长为( )
A. B.3 C. D.
20.如图,C为线段上一动点(不与点A,E重合),在同侧分别作正和正,与交于点O,与交于点P,与交于点Q,连接,以下五个结论:;;;;.一定成立的结论有( ).
A. B. C. D.
参考答案
1.解:A、图形不能找到一条直线,直线两旁的部分能够互相重合,不是轴对称图形,故此选项不符合题意;
B、图形不能找到一条直线,直线两旁的部分能够互相重合,不是轴对称图形,故此选项不符合题意;
C、图形不能找到一条直线,直线两旁的部分能够互相重合,不是轴对称图形,故此选项不符合题意;
D、图形能找到一条直线,使图形沿一条直线折叠,是轴对称图形,故此选项符合题意.
故选:D.
2.解:分如下两种情况:
①当腰为3,底为5,此时等腰三角形三边分别为3,3,5,且,故三角形存在,
因此它的周长为;
②当腰为5,底为3,此时等腰三角形三边分别为5,5,3,且,故三角形存在,
因此它的周长为;
综上所述,这个等腰三角形的周长为11或13,
故选:C.
3.解:①当是顶角时,底角,
②当是底角时,由三角形内角和定理可知,此种情况不存在,
它的底角是,
故选:A.
4.解:如图,∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故选:C.
5.解:∵为的垂直平分线,,
∴,,
∴,
∵,
∴,
∴.
故选:C.
6.解:延长交于,
平分,
,
,
,
,
,
,
的面积的面积,的面积的面积,
的面积的面积的面积的面积,
的面积的面积.
故选:B.
7.解:将直角边沿直线折叠,使它落在斜边上,且与重合,
,,
在和中,
,
,
,,
,
的面积是,
,
,
故选:A.
8.解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.
则充电桩应该安装在三条边的垂直平分线的交点处.
故选:D.
9.解:∵与关于直线对称,为上任一点,
又∵对称轴上的任何一点到两个对应点之间的距离相等,
∴,
∴是等腰三角形,选项A正确,不符合题意;
∵轴对称图形对应点所连的线段被对称轴垂直平分,
∴垂直平分,选项B正确,不符合题意;
∵轴对称图形对应的角、线段都相等,
∴与是全等三角形,周长也必然相等,选项C正确,不符合题意;
∵直线、关于直线对称,因此交点一定在上.
∴选项D错误,符合题意.
故选D.
10.解:连接,如图所示,
∵垂直平分,
∴,
∵,
∴,
∴是等腰三角形,
∵D为线段的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选:B;
11.解:∵是中的平分线,交AB于点E,,交AC于点F
∴.
又∵,
∴
解得.
故选:B.
12.解:连接,如下图:
∵
∴
∵平分
∴
又∵垂直平分
∴
∴
∴
∵平分,
∴垂直平分
∴
∴
由折叠的性质可得:,
∴
∴
故选:C
13.解:∵是等边三角形,正五边形的每个内角为,
∴,
∵,
∴.
故选:B.
14.解:∵是的垂直平分线,
∴,
∴,
∵的周长为24,则
∴
∴的周长为,
故选:B.
15.解: 平分,,
,,
,
,
,
,
故选:B.
16.解:如图所示.
网格中满足条件的点C有,共4个,
故选B.
17.解:,
,
,
,
,,,
.
在和中
,
,
.
,为中点,
.
,
,
,
,
的面积是.
故选:C.
18.解:分两种情况:(1)当为底角时,
①如图1,当时,
,
,
,
,
;
②如图2,当时,
,
,
,
;
③如图3,当时,
,,
,
,
;
(2)当为顶角时,
①如图4,,
,
,
,
,
;
②如图5,,
,
,
,
,
,
.
的度数为或或或或共5种.
故选:B.
19.解:作P关于的对称点D,作P关于的对称点E,连接交于M,交于N,连接,则此时的周长最小,
连接,
∵P、D关于对称,
∴,
同理,
∴,
∵P、D关于对称,
∴,
∵,
∴,
同理,
∴,
∵,
∴是等边三角形,
∴,
∵的周长是,
∴
故选:B.
20.解:①∵和是等边三角形,
∴,,,
∴,
在和中,
∴,
∴,,①正确;
②,
在和中,
∴,
∴,
∴,
∴,
∴,②正确;
③与②的过程同理得:,
∴,
③正确;
④∵,且,
∴,故④错误;
⑤∵,
∴,
∵是等边三角形,,
∴,
∴,
∴,
∴⑤正确.
故选:D
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
