第十二章全等三角形检测题(有答案)2023-2024学年度人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形检测题(有答案)2023-2024学年度人教版数学八年级上册 | 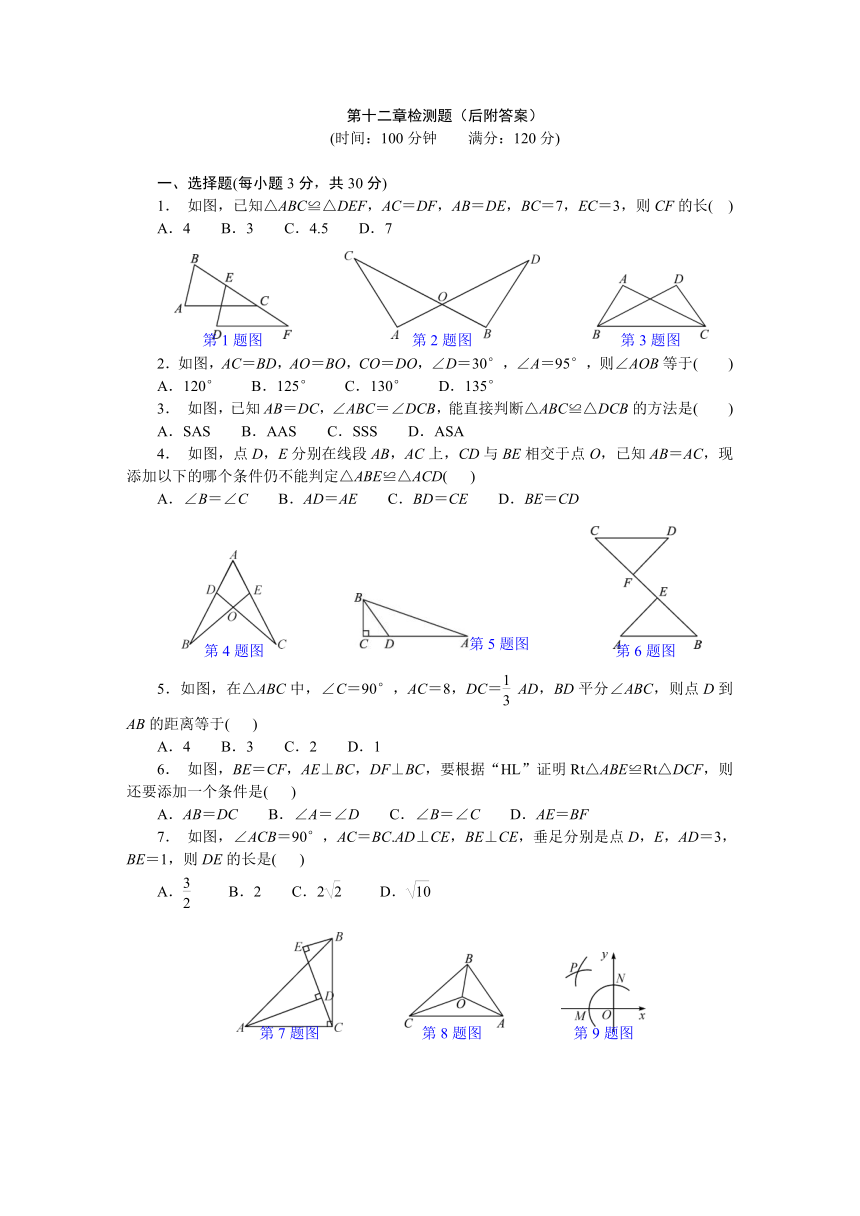 | |
| 格式 | DOC | ||
| 文件大小 | 328.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-01 18:00:06 | ||
图片预览




文档简介
第十二章检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1. 如图,已知△ABC≌△DEF,AC=DF,AB=DE,BC=7,EC=3,则CF的长( )
A.4 B.3 C.4.5 D.7
eq \o(\s\up7(),\s\do5(第1题图)) eq \o(\s\up7(),\s\do5(第2题图)) eq \o(\s\up7(),\s\do5(第3题图))
2.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( )
A.120° B.125° C.130° D.135°
如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
4. 如图,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
eq \o(\s\up7(),\s\do5(第4题图)) 第5题图 eq \o(\s\up7(),\s\do5(第6题图))
5.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=BF
7. 如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D,E,AD=3,BE=1,则DE的长是( )
A. B.2 C.2 D.
eq \o(\s\up7(),\s\do5(第7题图)) eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图)) eq \o(\s\up7(),\s\do5(第10题图))
8.如图,△ABC的三边AB,BC,CA的长分别为20,30,40,点O是△ABC三条角平分线的交点,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
9.如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
A.a=b B.2a+b=-1 C.2a-b=1 D.2a+b=1
10. 如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分,共15分)
11.已知△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,则△DEF的周长为__ __cm,面积为__ __cm2.
12.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C=__ __.
eq \o(\s\up7(),\s\do5(第12题图)) eq \o(\s\up7(),\s\do5(第13题图))
第14题图 第15题图
13.如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为__ __.
14.如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5 cm,则AE=__ __cm.
15.如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4,P在线段AB上(不与点A,B重合),Q在射线BD上,若△CAP与△PQB全等,则AP=__ __.
三、解答题(共75分)
16.(8分)如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,BC=EF.请探索BC与EF有怎样的位置关系?并说明理由.
17.(8分) 如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
18.(9分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E,求证:AE=AC.
19.(9分)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AB=EC.
(1)求证:△ABD≌△ECB;
(2)若∠BDC=65°,求∠DBC的度数.
20.(9分) 课上,老师提出了这样一个问题:
已知:如图,AD=AE,请你再添加一个条件,使得△ADB≌△AEC.
(1)同学们认为可以添加的条件并不唯一,你添加的条件是__________________,并完成证明;
(2)若添加的条件是OE=OD,证明:△ADB≌△AEC.
21.(10分)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
22.(10分)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
23.(12分)在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E,F分别在射线CA,BC上,且AE=CF,连接EF.
猜想:如图①,当点E,F分别在边CA和BC上时,线段DE与DF的大小关系为________;
探究:如图②,当点E,F分别在边CA,BC的延长线上时,判断线段DE与DF的大小关系,并加以证明;
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.
答案:
第十二章检测题
(时间:100分钟 满分:120分)
1. ( A )
2. ( B )
3. ( A )
4.( D )
5.( C )
6.( A )
7. ( B )
8. ( C )
9. ( B )
10. ( B )
11. __12__cm,面积为__6__cm2.
12. ∠C=__20°__.
13.__100°__.
14.__3__cm.
15.__8或6__.
16.
解:BC∥EF.理由:∵AE=BD,∴AE+EB=EB+BD,即AB=ED,在△CAB和△FDE中,∴△CAB≌△FDE(SSS),∴∠ABC=∠DEF,∴BC∥EF
17.
解:(1)∵CF∥AB,∴∠ADE=∠F,∠A=∠ECF.在△ADE和△CFE中,∴△ADE≌△CFE(AAS)
(2)∵△ADE≌△CFE,∴AD=CF=4.∴BD=AB-AD=5-4=1
18.
证明:∵DE⊥AB,∴∠AED=90°,∵∠ACB=90°,AD平分∠BAC,∴DE=DC.在Rt△ADE和Rt△ADC中,∴Rt△ADE≌Rt△ADC(HL),∴AE=AC
19.
解:(1)∵AD∥BC,∴∠ADB=∠EBC,在△ABD和△ECB中,∴△ABD≌△ECB(AAS)
(2)∵△ABD≌△ECB,∴BD=BC,∴∠BDC=∠BCD=65°,∴∠DBC=50°
20.
解:(1)添加的条件是AB=AC,证明:在△ADB和△AEC中,∴△ADB≌△AEC(SAS),故答案为:AB=AC(答案不唯一)
(2)连接OA,在△AEO和△ADO中,∴△AEO≌△ADO(SSS),∴∠AEO=∠ADO,在△ADB和△AEC中,∴△ADB≌△AEC(ASA)
21.
解:∵D为AB的中点,AB=10 cm,∴BD=AD=5 cm.设点P运动的时间是x s,若BD与CQ是对应边,则BD=CQ,∴5=3x,解得x=,此时BP=3×=5 (cm),CP=8-5=3 (cm),BP≠CP,故舍去;若BD与CP是对应边,则BD=CP,∴5=8-3x,解得x=1,此时BP=3×1=3(cm),CQ=3×1=3(cm),由SAS可证△BDP≌△CPQ.综上可得,当△BPD与△CQP全等时,点P运动的时间是1 s
22.
解:(1)BD=CE,BD⊥CE.证明:延长BD交CE于点M,易证△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵∠BME=∠MBC+∠BCM=∠MBC+∠ACE+∠ACB=∠MBC+∠ABD+∠ACB=∠ABC+∠ACB=90°,∴BD⊥CE (2)仍有BD=CE,BD⊥CE,理由同(1)
23.
解:猜想:DE=DF.连接CD,∵∠ACB=90°,AC=BC,D为AB中点,△ACD,△BCD都为等腰直角三角形,∴CD=AD,∠BCD=∠ACB=45°,∴∠EAD=∠FCD,在△AED和△CFD中,∴△AED≌△CFD(SAS),∴DE=DF,故答案为:DE=DF 探究:DE=DF,证明如下:连接CD,∵∠ACB=90°,AC=BC,D为AB中点,∴△ACD,△BCD都为等腰直角三角形,∴∠CAD=45°,AD=CD,∠BCD=∠ACB=45°,∵∠CAD+∠EAD=∠BCD+∠FCD=180°,∴∠EAD=∠FCD=135°,在△ADE和△CDF中,∴△ADE≌△CDF(SAS),∴DE=DF 应用:∵△ADE≌△CDF,∴∠ADE=∠CDF,∵∠ADC=90°,∴∠EDF=90°,∵DE=DF=4,∴S△DEF=DE·DF=×42=8
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1. 如图,已知△ABC≌△DEF,AC=DF,AB=DE,BC=7,EC=3,则CF的长( )
A.4 B.3 C.4.5 D.7
eq \o(\s\up7(),\s\do5(第1题图)) eq \o(\s\up7(),\s\do5(第2题图)) eq \o(\s\up7(),\s\do5(第3题图))
2.如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( )
A.120° B.125° C.130° D.135°
如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
4. 如图,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
eq \o(\s\up7(),\s\do5(第4题图)) 第5题图 eq \o(\s\up7(),\s\do5(第6题图))
5.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=BF
7. 如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D,E,AD=3,BE=1,则DE的长是( )
A. B.2 C.2 D.
eq \o(\s\up7(),\s\do5(第7题图)) eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图)) eq \o(\s\up7(),\s\do5(第10题图))
8.如图,△ABC的三边AB,BC,CA的长分别为20,30,40,点O是△ABC三条角平分线的交点,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
9.如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
A.a=b B.2a+b=-1 C.2a-b=1 D.2a+b=1
10. 如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分,共15分)
11.已知△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,则△DEF的周长为__ __cm,面积为__ __cm2.
12.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C=__ __.
eq \o(\s\up7(),\s\do5(第12题图)) eq \o(\s\up7(),\s\do5(第13题图))
第14题图 第15题图
13.如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为__ __.
14.如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5 cm,则AE=__ __cm.
15.如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4,P在线段AB上(不与点A,B重合),Q在射线BD上,若△CAP与△PQB全等,则AP=__ __.
三、解答题(共75分)
16.(8分)如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,BC=EF.请探索BC与EF有怎样的位置关系?并说明理由.
17.(8分) 如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
18.(9分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E,求证:AE=AC.
19.(9分)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AB=EC.
(1)求证:△ABD≌△ECB;
(2)若∠BDC=65°,求∠DBC的度数.
20.(9分) 课上,老师提出了这样一个问题:
已知:如图,AD=AE,请你再添加一个条件,使得△ADB≌△AEC.
(1)同学们认为可以添加的条件并不唯一,你添加的条件是__________________,并完成证明;
(2)若添加的条件是OE=OD,证明:△ADB≌△AEC.
21.(10分)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
22.(10分)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
23.(12分)在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E,F分别在射线CA,BC上,且AE=CF,连接EF.
猜想:如图①,当点E,F分别在边CA和BC上时,线段DE与DF的大小关系为________;
探究:如图②,当点E,F分别在边CA,BC的延长线上时,判断线段DE与DF的大小关系,并加以证明;
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.
答案:
第十二章检测题
(时间:100分钟 满分:120分)
1. ( A )
2. ( B )
3. ( A )
4.( D )
5.( C )
6.( A )
7. ( B )
8. ( C )
9. ( B )
10. ( B )
11. __12__cm,面积为__6__cm2.
12. ∠C=__20°__.
13.__100°__.
14.__3__cm.
15.__8或6__.
16.
解:BC∥EF.理由:∵AE=BD,∴AE+EB=EB+BD,即AB=ED,在△CAB和△FDE中,∴△CAB≌△FDE(SSS),∴∠ABC=∠DEF,∴BC∥EF
17.
解:(1)∵CF∥AB,∴∠ADE=∠F,∠A=∠ECF.在△ADE和△CFE中,∴△ADE≌△CFE(AAS)
(2)∵△ADE≌△CFE,∴AD=CF=4.∴BD=AB-AD=5-4=1
18.
证明:∵DE⊥AB,∴∠AED=90°,∵∠ACB=90°,AD平分∠BAC,∴DE=DC.在Rt△ADE和Rt△ADC中,∴Rt△ADE≌Rt△ADC(HL),∴AE=AC
19.
解:(1)∵AD∥BC,∴∠ADB=∠EBC,在△ABD和△ECB中,∴△ABD≌△ECB(AAS)
(2)∵△ABD≌△ECB,∴BD=BC,∴∠BDC=∠BCD=65°,∴∠DBC=50°
20.
解:(1)添加的条件是AB=AC,证明:在△ADB和△AEC中,∴△ADB≌△AEC(SAS),故答案为:AB=AC(答案不唯一)
(2)连接OA,在△AEO和△ADO中,∴△AEO≌△ADO(SSS),∴∠AEO=∠ADO,在△ADB和△AEC中,∴△ADB≌△AEC(ASA)
21.
解:∵D为AB的中点,AB=10 cm,∴BD=AD=5 cm.设点P运动的时间是x s,若BD与CQ是对应边,则BD=CQ,∴5=3x,解得x=,此时BP=3×=5 (cm),CP=8-5=3 (cm),BP≠CP,故舍去;若BD与CP是对应边,则BD=CP,∴5=8-3x,解得x=1,此时BP=3×1=3(cm),CQ=3×1=3(cm),由SAS可证△BDP≌△CPQ.综上可得,当△BPD与△CQP全等时,点P运动的时间是1 s
22.
解:(1)BD=CE,BD⊥CE.证明:延长BD交CE于点M,易证△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵∠BME=∠MBC+∠BCM=∠MBC+∠ACE+∠ACB=∠MBC+∠ABD+∠ACB=∠ABC+∠ACB=90°,∴BD⊥CE (2)仍有BD=CE,BD⊥CE,理由同(1)
23.
解:猜想:DE=DF.连接CD,∵∠ACB=90°,AC=BC,D为AB中点,△ACD,△BCD都为等腰直角三角形,∴CD=AD,∠BCD=∠ACB=45°,∴∠EAD=∠FCD,在△AED和△CFD中,∴△AED≌△CFD(SAS),∴DE=DF,故答案为:DE=DF 探究:DE=DF,证明如下:连接CD,∵∠ACB=90°,AC=BC,D为AB中点,∴△ACD,△BCD都为等腰直角三角形,∴∠CAD=45°,AD=CD,∠BCD=∠ACB=45°,∵∠CAD+∠EAD=∠BCD+∠FCD=180°,∴∠EAD=∠FCD=135°,在△ADE和△CDF中,∴△ADE≌△CDF(SAS),∴DE=DF 应用:∵△ADE≌△CDF,∴∠ADE=∠CDF,∵∠ADC=90°,∴∠EDF=90°,∵DE=DF=4,∴S△DEF=DE·DF=×42=8
